异常检测（2）Isolation Forest

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 2.2k 阅读时长 ≈ 4 分钟

一、Isolation Forest

1.1 概述

Isolation Forest算法梳理🌳

异常检测 (anomaly detection)，或者又被称为“离群点检测” (outlier detection)，是机器学习研究领域中跟现实紧密联系、有广泛应用需求的一类问题。但是，什么是异常，并没有标准答案，通常因具体应用场景而异。如果要给一个比较通用的定义，很多文献通常会引用 Hawkins 在文章开头那段话。很多后来者的说法，跟这个定义大同小异。这些定义虽然笼统，但其实暗含了认定“异常”的两个标准或者说假设：

孤立森林 (Isolation Forest) 是一个基于 Ensemble 的快速异常检测方法，具有线性时间复杂度和高精准度。其 可以用于网络安全中的攻击检测，金融交易欺计检测，疾病侦测，和噪声数据过滤等。

孤立森林算法的理论基础有两点：

  • 异常数据占总样本量的比列很小
  • 异常点的特征值与正常点的差异很大

1.2 iTREE的构建

\(i T r e e\) 是一棵随机二叉树, 每一个节点要么有两个孩子, 要么就是叶子节点。假设给定一堆数据集 \(\mathbb{D} ，\) 这里 \(\mathbb{D}\) 的所有属性都是连续型的变量, iTree 的构建过程如下:

  1. 随机选择一个属性 Attr ；

  2. 随机选择该属性的一个值 Value， \(\min \{A t t r\}<\) Value \(<\max \{\) Attr \(\}\) ；

  3. 根据 Attr 对每条记录进行分类，把 Attr 小于 Value 的记录放在左子树，把大于等于 Value 的记录放在右子树；

  4. 递归构造左右子树，直到满足下列条件：（1）传入的数据集只有一条记录或者多条同样的记录； (2) 树的 深度达到了限定深度。

img

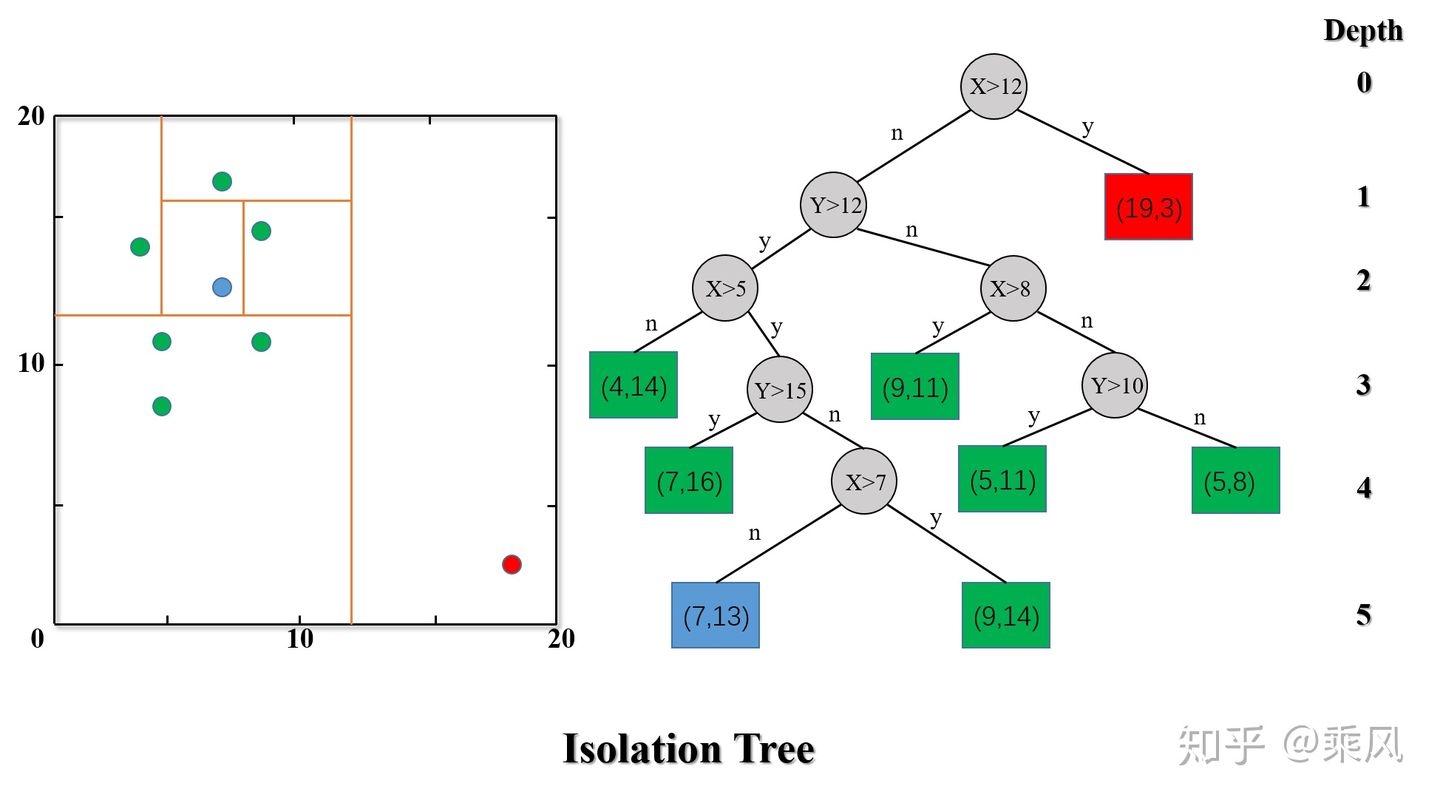
iTree 构建完成之后, 只需要追踪测试数据落在 iTree 哪个叶子节点上即可评估该数据是否为异常数据, 由图中 \(i T r e e\) 的构造过程可以发现异常数据通常会很快被分配到叶子节点上, 因此可以使用叶子结点到根结点的路径长 度（即边的条数） \(h(x)\) 来判断一条记录 \(x\) 是否是异常点。

1.3 iForest 构建

由于 \(i T r e e\) 是随机选择属性和随机选择属性值来构建的，因此可以预见对于单棵 \(i T r e e\) 的预测效果肯定不会很理 想，因此通过引入多棵 iTree 共同来预测那么从效果上看肯定会更具有说服力。iForest 和 Random Forest 的 方法有些类似, 都是通过随机采样, 利用部分采样数据来构造每一棵树, 以保证不同树之间的差异性。在构建 \(i\) Forest 的过程中有, 采样的样本大小 \(\psi\) 和 iTree 的数量 \(t\) 这两个超参数需要确定, 样本采样大小超过 256 效 果就提升不大了。

img

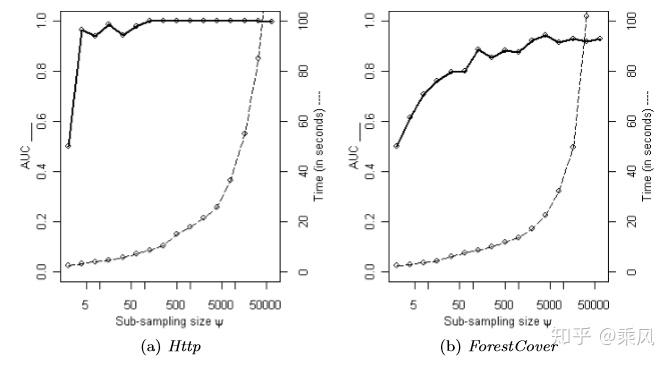
通过采样数据不仅可以降低计算时间的上面的浪费，而且还能够解决一些其它的小问题：

preview

左图是原始数据, 右图是经过采样了的数据, 蓝色代表正常样本, 红色代表异常样本。可以看出, 在采样之前, 正 常样本和异常样本出现了重叠, 因此很难分开, 但通过采样之后, 异常样本和正常样本可以明显的分开。 \(t\) 控制 了 iTree 的数量即 Ensemble size, 孤立森林算法提出者通过实验发现, 当 \(t=100\) 之前时, 算法就会收玫, 故 通常设置 \(t\) 为默认值 100 , 训练一个 iForest 最差情况下的时间复杂度为 \(\mathcal{O}\left(t \psi^2\right)\) 空间复杂度为 \(\mathcal{O}(t \psi)\) 。

1.4 评估

为了更好的归一化和比较, 孤立森林通过引入异常值函数 \(s(x, n)\) 来衡量记录 \(x\) 是否为异常点。

给定一个包含 \(n\) 个样本的数据集, 树的平均路径长度为： \(c(\mathrm{n})\) 。 \[ c(n)=2 H(n-1)-\frac{2(n-1)}{n} \] 其中, \(H(*)\) 为调和数, \(H(*)=\ln (*)+\xi, \xi\) 为欧拉常数, 约为 \(0.5772156649 。 c(n)\) 为给定样本数 \(n\) 时, 路径长度的平均值, 用来标准化记录 \(x\) 的路径长度 \(h(x)\) 。

故记录 \(x\) 的异常得分可以定义为： \(\mathbf{s}(\mathbf{x}, \mathbf{n})\). 其中, \(E(h(x))\) 为记录 \(x\) 在多个 \(i T r e e\) 中的路径长度的期望值。可视化 \(s(x, n)\) 与 \(E(h(x))\) 的关系: \[ s(x, n)=2^{-\frac{E(h(x))}{c(n)}} \]

img

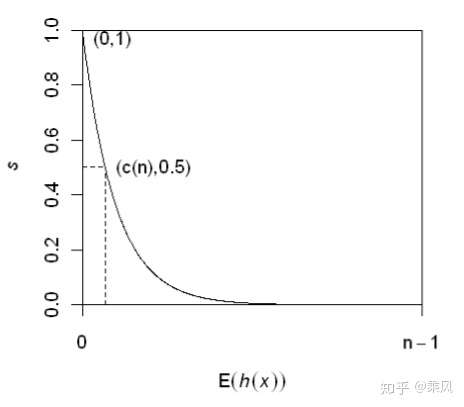
可以得出以下结论:

  • 当 \(E(h(x)) \rightarrow c(n)\) 时, \(s \rightarrow 0.5\) ， 即记录 \(x\) 的平均长度与树的平均路径长度相近时, 则不能区分是否为异 常;
  • 当 \(E(h(x)) \rightarrow 0 ， s \rightarrow 1\) ，即记录 \(x\) 的异常分数接近 1 时，被判定为异常数据；
  • 当 \(E(h(x)) \rightarrow n-1\) 时, \(s \rightarrow 0\) ， 被判定为正常数据。

参考文献

  • 孤立森林(isolation Forest)-一个通过瞎几把乱分进行异常检测的算法 - 小伍哥聊风控的文章 - 知乎 https://zhuanlan.zhihu.com/p/484495545
  • Isolation Forest算法梳理🌳Isolation Forest算法梳理🌳