特征工程（2）特征预处理

发表于 更新于 分类于 ， 阅读次数： 本文字数： 15k 阅读时长 ≈ 27 分钟

特征工程-特征处理

一、 数值类型处理

pandas 显示所有列：

1
2
3
4
5
6
#显示所有列
pd.set_option('display.max_columns', None)
#显示所有行
pd.set_option('display.max_rows', None)
#设置value的显示长度为100，默认为50
pd.set_option('max_colwidth',100)

pandas 查看缺失特征:

1
train.isnull().sum().sort_values(ascending = False) / train.shape[0]

pandas 查看某一列的分布:

1
df.loc[:,col_name].value_counts()

特征提取方式是可以深挖隐藏在数据背后更深层次的信息的。其次，数值类型数据也并不是直观看上去那么简单易用，因为不同的数值类型的计量单位不一样，比如个数、公里、千克、DB、百分比之类，同样数值的大小也可能横跨好几个量级，比如小到头发丝直径约为0.00004米， 大到热门视频播放次数成千上万次。

1.1 数据归一化

为什么要数据归一化？

深度学习（3）Normalization*.md

  • 可解释性：回归模型【无正则化】中自变量X的量纲不一致导致了回归系数无法直接解读或者错误解读；需要将X都处理到统一量纲下，这样才可比【可解释性】；取决于我们的逻辑回归是不是用了正则化。如果你不用正则，标准化并不是必须的，如果用正则，那么标准化是必须的。
  • 距离计算：机器学习任务和统计学任务中有很多地方要用到“距离”的计算，比如PCA、KNN，kmeans和SVM等等，假使算欧式距离，不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果；
  • 加速收敛：参数估计时使用梯度下降，在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。

需要归一化的模型：利用梯度下降法求解的模型一般需要归一化，线性回归、LR、SVM、KNN、神经网络

\[ \tilde{x}=\frac{x-\min (x)}{\max (x)-\min (x)} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np 
from sklearn.preprocessing import MinMaxScaler

# define data 
data = np.asarray([[100, 0.001], 
                   [8, 0.05], 
                   [50, 0.005], 
                   [88, 0.07], 
                   [4, 0.1]])
# define min max scaler
scaler = MinMaxScaler()
# transform data
scaled = scaler.fit_transform(data)

1.2 数据标准化

数据标准化是指通过改变数据的分布得到均值为0，标准差为1的服从标准正态分布的数据。主要目的是为了让不同特征之间具有相同的尺度（Scale），这样更有理化模型训练收敛。

1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler
# define standard scaler
scaler = StandardScaler()
# transform data
scaled = scaler.fit_transform(data) 
print(scaled)

1.3 对数转换

\(\log\) 函数的定义为 \(\log _a\left(\alpha^x\right)=x\), 其中 \(\mathrm{a}\) 是 \(\log\) 函数的底数, \(\alpha\) 是一个正常数, \(x\) 可以是任何正数。由于 \(\alpha^0=1\) \(a=10\) 时, 函数 \(\log _{10}(x)\) 可以将 \([1,10]\) 映射到[ \([0,1]\), 将 \([1,100]\) 映射到 \([1,2]\) 。换句话说, log函数压缩了大数的范 围, 扩大了小数的范围。 \(\mathrm{x}\) 越大, \(\log (\mathrm{x})\) 增量越慢。 \(\log (\mathrm{x})\) 函数的图像如下:

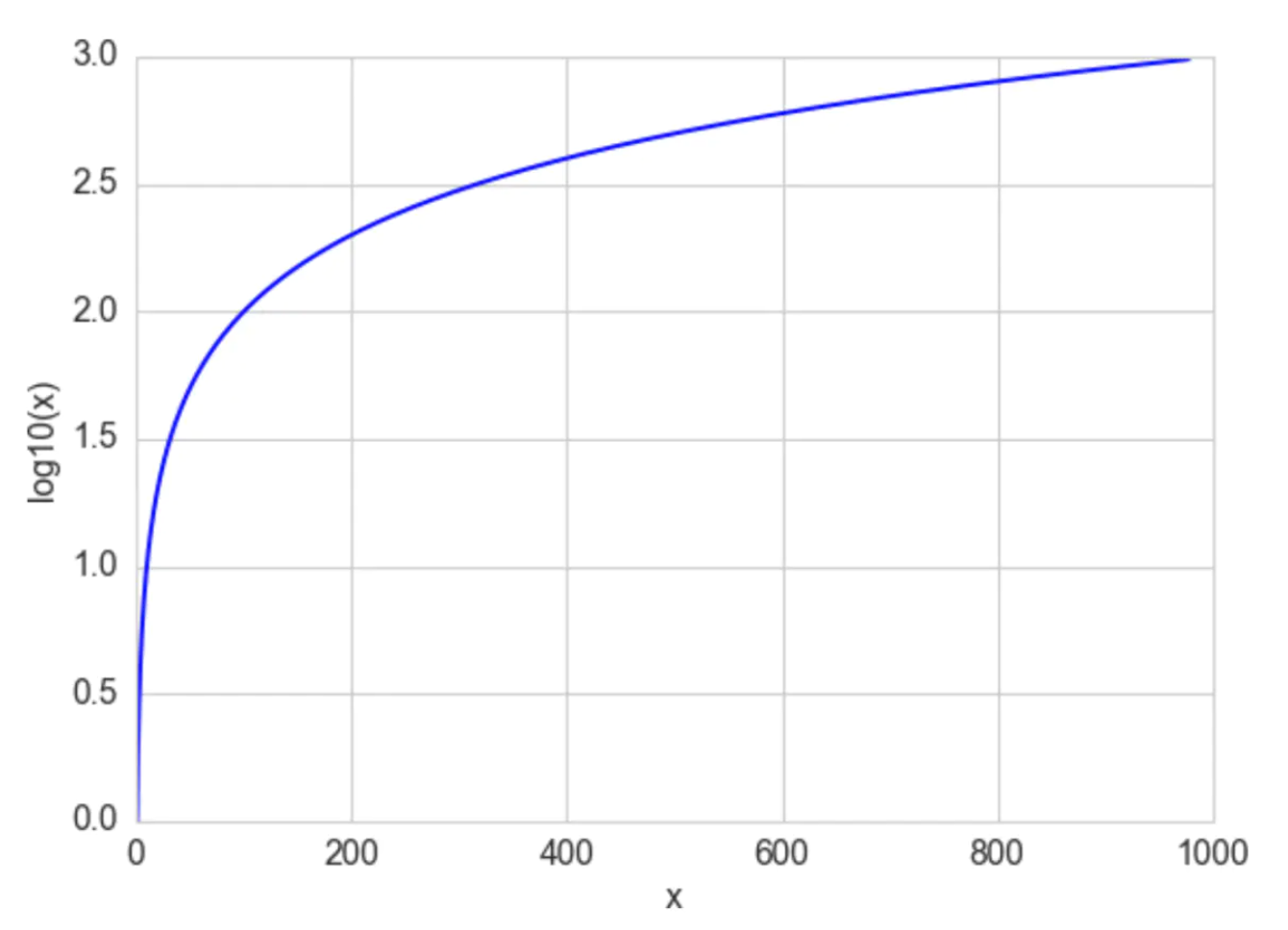
image-20220426154119370

Log函数可以极大压缩数值的范围，相对而言就扩展了小数字的范围。该转换方法适用于长尾分布且值域范围很大的特征，变换后的特征趋向于正态分布。对数值类型使用对数转换一般有以下几种好处：

  • 缩小数据的绝对数值
  • 取对数后，可以将乘法计算转换成加法计算
  • 在数据的整个值域中不同区间的差异带来的影响不同
  • 取对数后不会改变数据的性质和相关关系，但压缩了变量的尺度。
  • 得到的数据易消除异方差问题

二、序数和类别特征处理

本文主要说明特征工程中关于序数特征和类别特征的常用处理方法。主要包含LabelEncoder、One-Hot编码、DummyCoding、FeatureHasher以及要重点介绍的WOE编码。

2.1 序数特征处理

序数特征指的是有序但无尺度的特征。比如表示‘学历’的特征，'高中'、'本科'、'硕士'，这些特征彼此之间是有顺序关系的，但是特征本身无尺度，并且也可能不是数值类型。在实际应用中，一般是字符类型居多，为了将其转换成模型能处理的形式，通常需要先进行编码，比如LabelEncoding。如果序数特征本身就是数值类型变量，则可不进行该步骤。下面依次介绍序数特征相关的处理方式。

  • Label Encoding

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.preprocessing import LabelEncoder

x = ['a', 'b', 'a', 'c', 'b']
encoder = LabelEncoder()
x1 = encoder.fit_transform(x)

x2 = pd.Series(x).astype('category')
x2.cat.codes.values
# pandas 因子化
x2, uniques = pd.factorize(x)
# pandas 二值化
x2 = pd.Series(x)
x2 = (x2 >= 'b').astype(int) #令大于等于'b'的都为1

2.2 类别特征处理

类别特征由于没有顺序也没有尺度，因此处理较为麻烦，但是在CTR等领域却是非常常见的特征。比如商品的类型，颜色，用户的职业，兴趣等等。类别变量编码方法中最常使用的就是One-Hot编码，接下来结合具体实例来介绍。

  • One-Hot编码

One-Hot编码，又称为'独热编码'，其变换后的单列特征值只有一位是1。如下例所示，一个特征中包含3个不同的特征值(a,b,c)，编码转换后变成3个子特征，其中每个特征值中只有一位是有效位1。

1
2
3
4
5
6
7
from sklearn.preprocessing import LabelEncoder, OneHotEncoder

one_feature = ['b', 'a', 'c']
label_encoder = LabelEncoder()
feature = label_encoder.fit_transform(one_feature)
onehot_encoder = OneHotEncoder(sparse=False)
onehot_encoder.fit_transform(feature.reshape(-1, 1))

  • LabelBinarizer

sklearn中的LabelBinarizer也具有同样的作用，代码如下：

1
2
3
from sklearn.preprocessing import LabelBinarizer
feature = np.array(['b', 'a', 'c'])
LabelBinarizer().fit_transform(feature)

  • 虚拟编码Dummy Coding

同样，pandas中也内置了对应的处理方式,使用起来比Sklearn更加方便，产生n-1个特征。实例如下：

1
2
one_feature = ['b', 'a', 'c']
pd.get_dummies(one_feature, prefix='test') # 设置前缀test

  • 特征哈希（feature hashing）

按照上述编码方式，如果某个特征具有100个类别值，那么经过编码后将产生100个或99个新特征，这极大地增加了特征维度和特征的稀疏度，同时还可能会出现内存不足的情况。sklearn中的FeatureHasher接口采用了hash的方法，将不同的值映射到用户指定长度的数组中，使得输出特征的维度是固定的，该方法占用内存少，效率高，可以在多类别变量值中使用，但是由于采用了Hash函数的方式，所以具有冲突的可能，即不同的类别值可能映射到同一个特征变量值中。

Feature hashing(特征哈希): https://blog.csdn.net/laolu1573/article/details/79410187

https://scikit-learn.org/stable/modules/feature_extraction.html#feature-hashing

如何用通俗的语言解释CTR和推荐系统中常用的Feature Hashing技术以及其对应的优缺点？

1
2
3
4
5
6
from sklearn.feature_extraction import FeatureHasher

h = FeatureHasher(n_features=5, input_type='string')
test_cat = ['a','b','c','d','e','f','g','h','i','j','a','b']
f = h.transform(test_cat)
f.toarray()

如果hash的目标空间足够大，并且hash函数本身足够散列，不会损失什么特征信息。

feature hashing简单来说和kernal的思想是类似的，就是把输入的特征映射到一个具有一些我们期望的较好性质的空间上去。在feature hasing这个情况下我们希望目标的空间具有如下的性质：

  1. 样本无关的维度大小，因为当在线学习，或者数据量非常大，提前对数据观察开销非常大的时候，这可以使得我们能够提前给算法分配存储和切分pattern。大大提高算法的工程友好性。
  2. 这个空间一般来说比输入的特征空间维度小很多。
  3. 另外我们假设在原始的特征空间里，样本的分布是非常稀疏的，只有很少一部分子空间是被取值的。
  4. 保持内积的无偏（不变肯定是不可能的，因为空间变小了），否则很多机器学习方法就没法用了。

原理：假设输入特征是一个 \(\mathrm{N}\) 维的0/1取值的向量 \(\mathrm{x}_{\circ} 一 个 \mathrm{~N}->\mathrm{M}\) 的哈希函数 \(\mathrm{h}\) 。那么 \(\phi_j=\sum_{h(i)=j} x_i\)

好处：

  • 从某种程度上来讲，使得训练样本的特征在对应空间里的分布更均匀了。这个好处对于实际训练过程是非常大的，某种程度上起到了shuffle的作用。
  • 特征的空间变小了，而且是一个可以预测的大小。比如说加入输入特征里有个东西叫做user_id，那么显然你也不知道到底有多少userid的话，你需要先扫描一遍并且分配足够的空间给到它不然学着学着oom了。你也不能很好地提前优化分片。
  • 对在线学习非常友好。

坏处：

  • 会给debug增加困难，为了debug你要保存记录h计算的过程数据，否则如果某个特征有毛病，你怎么知道到底是哪个原始特征呢？
  • 没选好哈希函数的话，可能会造成碰撞，如果原始特征很稠密并且碰撞很严重，那可能会带来坏的训练效果。
1
2
3
4
5
6
7
8
9
10
def hashing_vectorizer(features, N):
  	x = [0] * N
    for f in features:
      	h = hash(f)
        idx = h % N
        if xt(f)  1: # xt 2值hash函数减少hash冲突
          	x[idx] += 1
        else:
         		x[idx] -= 1
    return x

  • 多类别值处理方式 -- 基于统计的编码方法

当类别值过多时，One-Hot 编码或者Dummy Coding都可能导致编码出来的特征过于稀疏，其次也会占用过多内存。如果使用FeatureHasher，n_features的设置不好把握，可能会造成过多冲突，造成信息损失。这里提供一种基于统计的编码方法，包括基于特征值的统计或者基于标签值的统计——基于标签的编码。

1
2
3
4
5
import seaborn as sns

test = ['a','b','c','d','e','a','a','c']
df = pd.DataFrame(test, columns=['alpha'])
sns.countplot(df['alpha'])

image-20220426130800412

首先我们将每个类别值出现的频数计算出来，比如我们设置阈值为1，那么所有小于阈值1的类别值都会被编码为同一类，大于1的类别值会分别编码，如果出现频数一样的类别值，既可以都统一分为一个类，也可以按照某种顺序进行编码，这个可以根据业务需要自行决定。那么根据上图，可以得到其编码值为：

\[ \left\{a^{\prime}: 0, ' c^{\prime}: 1, ' e^{\prime}: 2, ' b^{\prime}: 2, ' d ': 2\right\} \] 即（a,c）分别编码为一个不同的类别，（e,b,d）编码为同一个类别。

2.3 二阶

w * h = s

三、 特征离散化处理方法

特征离散化指的是将连续特征划分离散的过程：将原始定量特征的一个区间一一映射到单一的值。离散化过程也被表述成分箱（Binning）的过程。特征离散化常应用于逻辑回归和金融领域的评分卡中，同时在规则提取，特征分类中也有对应的应用价值。本文主要介绍几种常见的分箱方法，包括等宽分箱、等频分箱、信息熵分箱、基于决策树分箱、卡方分箱等。

可以看到在分箱之后，数据被规约和简化，有利于理解和解释。总来说特征离散化，即 分箱之后会带来如下优势：

  • 有助于模型部署和应用，加快模型迭代
  • 增强模型鲁棒性
  • 增加非线性表达能力：连续特征不同区间对模型贡献或者重要程度不一样时，分箱后不同的权重能直接体现这种差异，离散化后的特征再进行特征 交叉衍生能力会进一步加强。
  • 提升模型的泛化能力
  • 扩展数据在不同各类型算法中的应用范围

当然特征离散化也有其缺点，总结如下：

  • 分箱操作必定会导致一定程度的信息损失
  • 增加流程：建模过程中加入了额外的的离散化步骤
  • 影响模型稳定性： 当一个特征值处于分箱点的边缘时，此时微小的偏差会造成该特征值的归属从一箱跃迁到另外一箱，影响模型的稳定性。

3.1 等宽分箱（Equal-Width Binning)

等宽分箱指的是每个分隔点或者划分点的距离一样，即等宽。实践中一般指定分隔的箱数，等分计算后得到每个分隔点。例如将数据序列分为n份，则 分隔点的宽度计算公式为： \[ w=\frac{\max -\min }{n} \] 这样就将原始数据划分成了n个等宽的子区间，一般情况下，分箱后每个箱内的样本数量是不一致的。使用pandas中的cut函数来实现等宽分箱，代码如下：

1
value, cutoff = pd.cut(df['mean radius'], bins=4, retbins=True, precision=2)

等宽分箱计算简单，但是当数值方差较大时，即数据离散程度很大，那么很可能出现没有任何数据的分箱，这个问题可以通过自适应数据分布的分箱方法--等频分箱来避免

3.2 等频分箱（Equal-Frequency Binning）

等频分箱理论上分隔后的每个箱内得到数据量大小一致，但是当某个值出现次数较多时，会出现等分边界是同一个值，导致同一数值分到不同的箱内，这是不正确的。具体的实现可以去除分界处的重复值，但这也导致每箱的数量不一致。如下代码：

1
2
3
s1 = pd.Series([1,2,3,4,5,6])
value, cutoff = pd.qcut(s1, 3, retbins=True)
sns.countplot(value)

上述的等宽和等频分箱容易出现的问题是每箱中信息量变化不大。例如，等宽分箱不太适合分布不均匀的数据集、离群值；等频方法不太适合特定的值占比过多的数据集，如长尾分布。

3.3 信息熵分箱【有监督】

如果分箱后箱内样本对y的区分度好，那么这是一个好的分箱。通过信息论理论，我们可知信息熵衡量了这种区分能力。当特征按照某个分隔点划分为上下两部分后能达到最大的信息增益，那么这就是一个好的分隔点。由上可知，信息熵分箱是有监督的分箱方法。 其实决策树的节点分裂原理也是基于信息熵。

首先我们需要明确信息熵和信息增益的计算方式, 分别如下: \[ \begin{gathered} \operatorname{Entropy}(y)=-\sum_{i=1}^m p_i \log _2 p_i \\ \operatorname{Gain}(x)=\operatorname{Entropy}(y)-\operatorname{Infos}_{\text {split }}(x) \end{gathered} \] 在二分类问题中, \(m=2\) 。信息增益的物理含义表达为： \(x\) 的分隔带来的信息对 \(y\) 的不确定性带来的增益。 对于二值化的单点分隔, 如果我们找到一个分隔点将数据一分为二, 分成 \(P_1\) 和 \(P_2\) 两部分, 那么划分后的信息熵 的计算方式为: \[ \operatorname{Info}_{\text {split }}(x)=P 1_{\text {ratio }} \operatorname{Entropy}\left(x_{p 1}\right)+P 2_{\text {ratio }} \operatorname{Entropy}\left(x_{p 2}\right) \] 同时也可以看出，当分箱后，某个箱中的标签y的类别（0或者1）的比例相等时，其熵值最大，表明此特征划分几 乎没有区分度。而当某个箱中的数据的标签 \(y\) 为单个类别时, 那么该箱的熵值达到最小的 0 , 即纯度最纯, 最具区 分度。从结果上来看, 最大信息增益对应分箱后的总熵值最小。

3.4 决策树分箱【有监督】

由于决策树的结点选择和划分也是根据信息熵来计算的，因此我们其实可以利用决策树算法来进行特征分箱，具体做法如下：

还是以乳腺癌数据为例，首先取其中‘mean radius’字段，和标签字段‘target’来拟合一棵决策树，代码如下：

1
2
3
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(criterion='entropy', max_depth=3) # 树最大深度为3
dt.fit(df['mean radius'].values.reshape(-1, 1), df['target'])

接着我们取出这课决策树的所有叶节点的分割点的阈值，如下：

1
2
3
qts = dt.tree_.threshold[np.where(dt.tree_.children_left > -1)]
qts = np.sort(qts)
res = [np.round(x, 3) for x in qts.tolist()]

3.5 卡方分箱 【有监督】

特征选择之卡方分箱、WOE/IV - 云水僧的文章 - 知乎 https://zhuanlan.zhihu.com/p/101771771

卡方检验可以用来评估两个分布的相似性，因此可以将这个特性用到数据分箱的过程中。卡方分箱认为：理想的分箱是在同一个区间内标签的分布是相同的; 卡方分布是概率统计常见的一种概率分布，是卡方检验的基础。

布定义为: 若n个独立的随机变量 \(Z_1, Z_2, \ldots, Z_k\) 满足标准正态分布 \(N(0,1)\), 则 \(\mathrm{n}\) 个随机变量的平方和 \(X=\sum_{i=0}^k Z_i^2\) 为服从自由度为 \(\mathrm{k}\) 的卡方分布, 记为 \(X \sim \chi^2\) 。参数 \(\mathrm{n}\) 称为自由度（样本中独立或能自由变化的自变 量的个数), 不同的自由度是不同的分布。

卡方检验：卡方检验属于非参数假设检验的一种，其本质都是度量频数之间的差异。其假设为：观察频数与期望 频数无差异或者两组变量相互独立不相关。 \[ \chi^2=\sum \frac{(O-E)^2}{E} \]

  • 卡方拟合优度检验：用于检验样本是否来自于某一个分布，比如检验某样本是否为正态分布
  • 独立性卡方检验，查看两组类别变量分布是否有差异或者相关，以列联表的形式比较。以列联表形式的卡方检验中，卡方统计量由上式给出。

步骤：

卡方分箱是自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。基本思想: 对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。

理想的分箱是在同一个区间内标签的分布是相同的。卡方分箱就是不断的计算相邻区间的卡方值（卡方值越小表示分布越相似），将分布相似的区间（卡方值最小的）进行合并，直到相邻区间的分布不同，达到一个理想的分箱结果。下面用一个例子来解释：

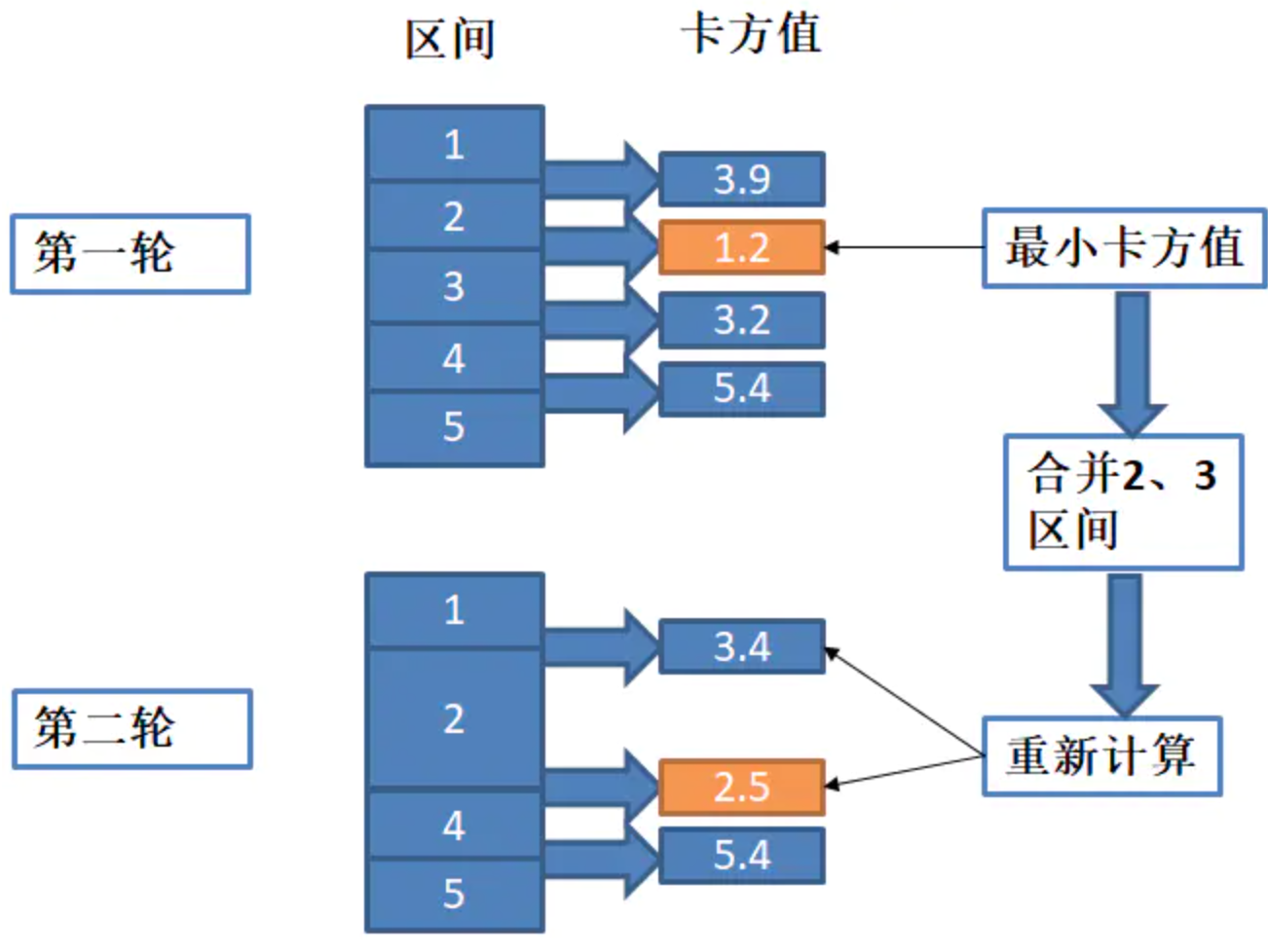
image-20220708173638301

由上图，第一轮中初始化是5个区间，分别计算相邻区间的卡方值。找到1.2是最小的，合并2、3区间，为了方便，将合并后的记为第2区间，因此得到4个区间。第二轮中，由于合并了区间，影响该区间与前面的和后面的区间的卡方值，因此重新计算1和2,2和4的卡方值，由于4和5区间没有影响，因此不需要重新计算，这样就得到了新的卡方值列表，找到最小的取值2.5，因此该轮会合并2、4区间，并重复这样的步骤，一直到满足终止条件。

3.6 WOE编码 【有监督】

风控模型—WOE与IV指标的深入理解应用: https://zhuanlan.zhihu.com/p/80134853

WOE (Weight of Evidence, 证据权重）编码利用了标签信息, 属于有监督的编码方式。该方式广泛用于金融领 域信用风险模型中, 是该领域的经验做法。下面先给出WOE的计算公式: \[ W O E_i=\ln \left\{\frac{P_{y 1}}{P_{y 0}}\right\}=\ln \left\{\frac{B_i / B}{G_i / G}\right\} \] \(W O E_i\) 值可解释为第 \(i\) 类别中好坏样本分布比值的对数。其中各个分量的解释如下: - \(P_{y 1}\) 表示该类别中坏样本的分布 - \(P_{y 0}\) 表示该类别中好样本的分布 - \(B_i / B\) 表示该类别中坏样本的数量在总体坏样本中的占比 - \(G_i / G\) 表示该类别中好样本的数量在总体好样本中的占比

很明显，如果整个分数的值大于1，那么WOE值为正，否则为负，所以WOE值的取值范围为正负无穷。 WOE值直观上表示的实际上是“当前分组中坏客户占所有坏客户的比例”和“当前分组中好客户占所有坏客户的比例”的差异。转化公式以后，也可以理解为：当前这个组中坏客户和好客户的比值，和所有样本中这个比值的差异。这个差异为这两个比值的比值，再取对数来表示的。 WOE越大，这种差异越大，这个分组里的样本坏样本可能性就越大，WOE越小，差异越小，这个分组里的坏样本可能性就越小。

1
2
3
4
5
6
7
np.random.seed(0)
# 随机生成1000行数据
df = pd.DataFrame({
    'x': np.random.choice(['R','G','B'], 1000),
    'y': np.random.randint(2, size=1000)
})
df.head()

四、缺失值处理解析

看不懂你打我，史上最全的缺失值解析: https://zhuanlan.zhihu.com/p/379707046

https://zhuanlan.zhihu.com/p/137175585

机器学习模型 是否支持缺失值
XGBoost 是
LightGBM 是
线性回归 否
逻辑回归（LR） 否
随机森林（RF） 否
SVM 否
因子分解机(FM) 否
朴实贝叶斯（NB） 否

4.1 缺失值的替换

scikit-learn中填充缺失值的API是Imputer类，使用方法如下：

参数strategy有三个值可选：mean(平均值)，median(中位数)，most_frequent(众数)

1
2
3
4
5
6
7
8
rom sklearn.preprocessing import Imputer
import numpy as np
# 缺失值填补的时候必须得是float类型
# 缺失值要填充为np.nan，它是浮点型，strategy是填充的缺失值类型，这里填充平均数，axis代表轴，这里第0轴是列
im = Imputer(missing_values='NaN',strategy='mean',axis=0)
data = im.fit_transform([[1, 2], 
                         [np.nan, 3], 
                         [7, 6]])

4.2 缺失值的删除

五、异常值处理

数据预处理Q&A

 1、LR为什么要离散化？

[学习] 连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？

问题描述：发现CTR预估一般都是用LR，而且特征都是离散的，为什么一定要用离散特征呢？这样做的好处在哪里？求大拿们解答。

答案一（严林）：

在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

  1. 离散特征的增加和减少都很容易，易于模型的快速迭代；
  2. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
  3. 【鲁棒性】离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则为0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
  4. 【模型假设】逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有独立的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
  5. 【特征交叉】离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
  6. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻的样本会刚好相反，所以怎么划分区间是门学问；
  7. 特征离散化以后，起到了简化逻辑回归模型的作用，降低了模型过拟合的风险；
李沐曾经说过：模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型”同“少量连续特征+复杂模型”的权衡。

这里我写下我关于上面某些点的理解，有问题的欢迎指出：

  1. 假设目前有两个连续的特征：『年龄』和『收入』，预测用户的『魅力指数』；

第三点: LR是广义线性模型，因此如果特征『年龄』不做离散化直接输入，那么只能得到『年龄』和魅力指数的一个线性关系。但是这种线性关系是不准确的，并非年龄越大魅力指一定越大；如果将年龄划分为M段，则可以针对每段有一个对应的权重；这种分段的能力为模型带来类似『折线』的能力，也就是所谓的非线性 连续变量的划分，naive的可以通过人为先验知识划分，也可以通过训练单特征的决策树桩，根据Information Gain/Gini系数等来有监督的划分。 假如『年龄』离散化后，共有N段，『收入』离散化后有M段；此时这两个离散化后的特征类似于CategoryFeature，对他们进行OneHotEncode，即可以得到 M + N的 01向量；例如： 0 1 0 0， 1 0 0 0 0； 第四点: 特征交叉，可以理解为上述两个向量的互相作用，作用的方式可以例如是 &和|操作（这种交叉方式可以产生一个 M * N的01向量；） 上面特征交叉，可以类比于决策树的决策过程。例如进行&操作后，得到一个1，则可以认为产生一个特征 （a < age < b && c < income < d）;将特征空间进行的非线性划分，也就是所谓的引入非线性；

答案二（周开拓）：

机器学习里当然并没有free lunch，一个方法能work，必定是有假设的。如果这个假设和真实的问题及数据比较吻合，就能work。

对于LR这类的模型来说，假设基本如下：

  • 局部平坦性，或者说连续性。对于连续特征x来说，在任何一个取值x0的邻域附近，这个特征对预估目标y的影响也在一个足够小的邻域内变化。比如，人年龄对点击率的影响，x0=30岁假设会产生一定的影响，那么x=31或者29岁，这个影响和x0=30岁的影响差距不会太大；
  • x对y的影响，这个函数虽然局部比较平坦，但是不太规律，如果你知道这个影响是个严格的直线（或者你有先验知识知道这个影响一定可以近似于一个参数不太多的函数），显然也没必要去做离散化。当然这条基本对于绝大多数问题都是成立的，因为基本没有这种好事情。

假设一个最简单的问题，binary classification，y=0/1，x是个连续值。你希望学到一个logloss足够小的y=f(x)。

那么有一种做法就是，在数据轴上切若干段，每一段观察训练样本里y为1的比例，以这个比例作为该段上y=f(x)的值。这个当然不是LR训练的过程，但是就是离散化的思想。你可以发现：

  • 如果每一段里面都有足够多的样本，那么在这一段里的y=f(x)值的点估计就比较可信；
  • 如果x在数轴上分布不太均匀，比如是指数分布或者周期分布的，这么做可能会有问题，因而你要先对x取个log，或者去掉周期性；

这就告诉了你应该怎么做离散化： 尽可能保证每个分段里面有足够多的样本，尽量让样本的分布在数轴上均匀一些。

结语：本质上连续特征离散化，可以理解为连续信号怎么转化为数字信号，好比我们计算机画一条曲线，也是变成了画一系列线段的问题。用分段函数来表达一个连续的函数在大多数情况下，都是work的。想取得好的效果需要：

  • 你的分段足够小，以使得在每个分段内x对y的影响基本在一个不大的邻域内，或者你可以忍受这个变化的幅度；
  • 你的分段足够大，以使得在每个分段内有足够的样本，以获得可信的f(x)也就是权重；
  • 你的分段策略使得在每个x的分段中，样本的分布尽量均匀（当然这很难），一般会根据先验知识先对x做一些变化以使得变得均匀一些；
  • 如果你有非常强的x对y的先验知识，比如严格线性之类的，也未必做离散化，但是这种先验在计算广告或者推荐系统里一般是不存在的，也许其他领域比如CV之类的里面是可能存在的；

最后还有个特别大的LR用离散特征的好处就是LR的特征是并行的，每个特征是并行同权的，如果有异常值的情况下，如果这个异常值没见过，那么LR里因为没有这个值的权重，最后对score的贡献为0，最多效果不够好，但是不会错的太离谱。另外，如果你debug，很容易查出来是哪个段上的权重有问题，比较好定位和解决。

2、树模型为什么离散化？

Cart树的离散化：

分类：

  • 如果特征值是连续值：CART的处理思想与C4.5是相同的，即将连续特征值离散化。唯一不同的地方是度量的标准不一样， CART采用基尼指数，而C4.5采用信息增益比。

  • 如果当前节点为连续属性，CART树中该属性（剩余的属性值）后面还可以参与子节点的产生选择过程。

回归：

对于连续值的处理, CART 分类树采用基尼系数的大小来度量特征的各个划分点。在回归模型中, 我们使用常见的和方差度量方式, 对于任意划分特征 \(\mathrm{A}\), 对应的任意划分点 \(\mathrm{s}\) 两边划分成的数据集 \(D_1\) 和 \(D_2\), 求出使 \(D_1\) 和 \(D_2\) 各自集合的均方差最小, 同时 \(D_1\) 和 \(D_2\) 的均方差之和最小所对应的特征和特征值划分点。表达式为: \[ \min _{a, s}\left[\min _{c_1} \sum_{x_i \in D_1}\left(y_i-c_1\right)^2+\min _{c_2} \sum_{x_i \in D_2}\left(y_i-c_2\right)^2\right] \] 其中, \(c_1\) 为 \(D_1\) 数据集的样本输出均值, \(c_2\) 为 \(D_2\) 数据集的样本输出均值。

LGB直方图算法优点：

内存小、复杂度降低、直方图加速【分裂、并行通信、缓存优化】

  • 内存消耗降低。预排序算法需要的内存约是训练数据的两倍（2x样本数x维度x4Bytes），它需要用32位浮点来保存特征值，并且对每一列特征，都需要一个额外的排好序的索引，这也需要32位的存储空间。对于 直方图算法，则只需要(1x样本数x维 度x1Bytes)的内存消耗，仅为预排序算法的1/8。因为直方图算法仅需要存储特征的 bin 值(离散化后的数值)，不需要原始的特征值，也不用排序，而bin值用8位整型存储就足够了。

  • 算法时间复杂度大大降低。决策树算法在节点分裂时有两个主要操作组成，一个是“寻找分割点”，另一个是“数据分割”。从算法时间复杂度来看，在“寻找分割点”时，预排序算法对于深度为\(k\)的树的时间复杂度：对特征所有取值的排序为\(O(NlogN)\)，\(N\)为样本点数目，若有\(D\)维特征，则\(O(kDNlogN)\)，而直方图算法需要\(O(kD \times bin)\) (bin是histogram 的横轴的数量，一般远小于样本数量\(N\))。

  • 直方图算法还可以进一步加速【两个维度】。一个容易观察到的现象：一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到（分裂时左右集合）。通常构造直方图，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的\(k\)个bin。利用这个方法，LightGBM可以在构造一个叶子的直方图后，可以用非常微小的代价得到它兄弟叶子的直方图，在速度上可以提升一倍。

  • 数据并行优化，用 histgoram 可以大幅降低通信代价。用 pre-sorted 算法的话，通信代价是非常大的（几乎是没办法用的）。所以 xgoobst 在并行的时候也使用 histogram 进行通信。

  • 缓存优化：上边说到 XGBoost 的预排序后的特征是通过索引给出的样本梯度的统计值，因其索引访问的结果并不连续，XGBoost 提出缓存访问优化算法进行改进。 LightGBM 所使用直方图算法对 Cache 天生友好所有的特征都采用相同的方法获得梯度，构建直方图时bins字典同步记录一阶导、二阶导和个数，大大提高了缓存命中；因为不需要存储特征到样本的索引，降低了存储消耗，而且也不存在 Cache Miss的问题。

3、归一化？

参考文献

  • 机器学习中的特征工程（四）---- 特征离散化处理方法：https://www.jianshu.com/p/918649ce379a

  • 机器学习中的特征工程（三）---- 序数和类别特征处理方法：https://www.jianshu.com/p/3d828de72cd4

  • 机器学习中的特征工程（二）---- 数值类型数据处理：https://www.jianshu.com/p/b0cc0710ef55

  • 机器学习中的特征工程（一）---- 概览：https://www.jianshu.com/p/172677f4ea4c

  • 特征工程完全手册 - 从预处理、构造、选择、降维、不平衡处理，到放弃：https://zhuanlan.zhihu.com/p/94994902

  • 这9个特征工程使用技巧，解决90%机器学习问题！ - Python与数据挖掘的文章 - 知乎 https://zhuanlan.zhihu.com/p/462744763