聚类（3）HDBSCAN

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 5.4k 阅读时长 ≈ 10 分钟

一、HDBSCAN聚类

HDBSCAN 是由 Campello、Moulavi 和 Sander 开发的聚类算法。它通过将 DBSCAN 转换为层次聚类算法，然后用一种稳定的聚类技术提取出一个扁平的聚类来扩展 DBSCAN。这篇文章的目标是让你大致了解这个算法的工作原理及其背后的动机。与 HDBSCAN 的原论文不一样，我们这里将不将 DBSCAN 进行对照分析。作者这里更倾向将这算法类比成一种扁平聚类提取方法（ Robust Single Linkage ）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.datasets as data
%matplotlib inline
sns.set_context('poster')
sns.set_style('white')
sns.set_color_codes()
plot_kwds = {'alpha' : 0.5, 's' : 80, 'linewidths':0}

moons, _ = data.make_moons(n_samples=50, noise=0.05)
blobs, _ = data.make_blobs(n_samples=50, centers=[(-0.75,2.25), (1.0, 2.0)], cluster_std=0.25)
test_data = np.vstack([moons, blobs])
plt.scatter(test_data.T[0], test_data.T[1], color='b', **plot_kwds)

import hdbscan
clusterer = hdbscan.HDBSCAN(min_cluster_size=5, gen_min_span_tree=True)
clusterer.fit(test_data)

现在我们已经对数据聚类完了——但实际发生了什么我们还不知道。我们将拆解成下面5个步骤来进行分析：

  1. 根据 密度/稀疏度 进行空间转换。
  2. 构建基于加权距离图的最小生成树。
  3. 构建组件之间的层次簇结构。
  4. 用最小簇大小压缩层次聚类。
  5. 利用压缩好的生成树进行分类。

1.1 空间转换

聚类时我们希望在稀疏带噪声的数据中找到密度更高的族类——噪声的假设很重要：因为在真实情况下，数据都比较复杂，会有异常值的、缺失的数据和噪声等情况。算法的核心是单链聚类，它对噪声非常敏感：如果噪声数据点放在两个岛屿之间，可能就会将它们连在一起（也就是本来是两个族类的被分成一个）。显然，我们希望我们的算法对噪声具有鲁棒性，因此我们需要在运行单链算法之前找到一种方法来减少噪声。（作者用岛屿来比喻族类，海洋来表示噪声，下面“海洋”和“岛屿”代表这个意思。）

我们要如何在不进行聚类的情况下找出“海洋”和“岛屿”？只要我们能够估算出样本集的密度，我们就可以认为密度较低的点都是“海洋”。要注意的是这里的目标不是完全区分出“海洋”和“岛屿”——现在只是聚类的初始步骤，并不是最终的输出——现在只是为了使我们的聚类中心对噪声更加鲁棒。因此，要识别出“海洋”的话，我们可以降低海平面（也就是加大容错范围）。出于实际目的，这意味着使每个“海洋”之间以及“海洋”与“岛屿”之间的距离会增加。

当然这只是直觉。它在实际中是如何工作的？我们需要一个计算量少的密度估计方式，简单到只要计算 k 个最近邻点的距离就可以。 我们可以直接从一个距离矩阵（不管怎样后面都要生成的）中地读取到这个距离；或者，如果我们的指标支持（并且维度较低），用 kd-trees 来做这种检索就很适合。下面正式将点 x 的参数 k 定义为核心距离, 并表示为 \(\operatorname{core}_k(x)\) (与DBSCAN、LOF 和 HDBSCAN 文献一样）。现在我们需要一种降维方法来拉开点之 间的距离（相对高维距离）。简单的方法是定义一种新距离公式，我们将其称为（与论文一样)相互可达距离 (mutual reachability distance)。相互可达距离的定义如下: \[ d_{\mathrm{mreach}-k}(a, b)=\max \left\{\operatorname{core}_k(a), \operatorname{core}_k(b), d(a, b)\right\} \] 其中 d(a,b) 是 a 和 b 之间的原始距离。在这个度量下，密集点（具有低核心距离）之间的距离保持不变，但稀疏的点与其他点的距离被拉远到用core距离来计算。这有效地“降低了海平面”，减少稀疏的“海”点，同时使“陆地”保持原状。需要注意的是，显然 k 取值很关键；较大的 k 值将更多的点圈到“海”中。下面用图片来解析更容易理解，先让k=5。然后对于给定的点，我们可以为核心距离绘制一个圆刚好圈到第六个临近点（包括点本身），如下所示：

img

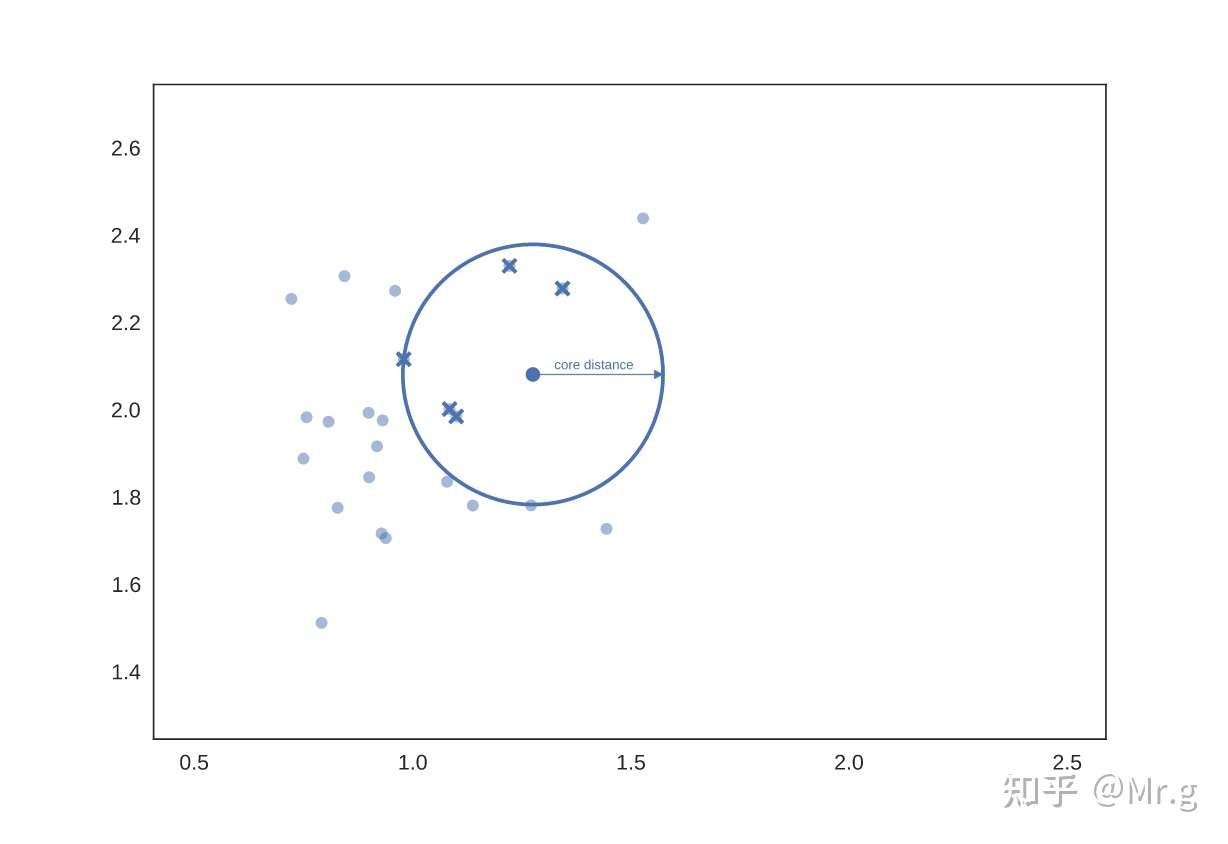
再选择另一个点，进行同样的操作，这次选到另一组临近点集合（其中一些点可能是上一组的临近点）。

img

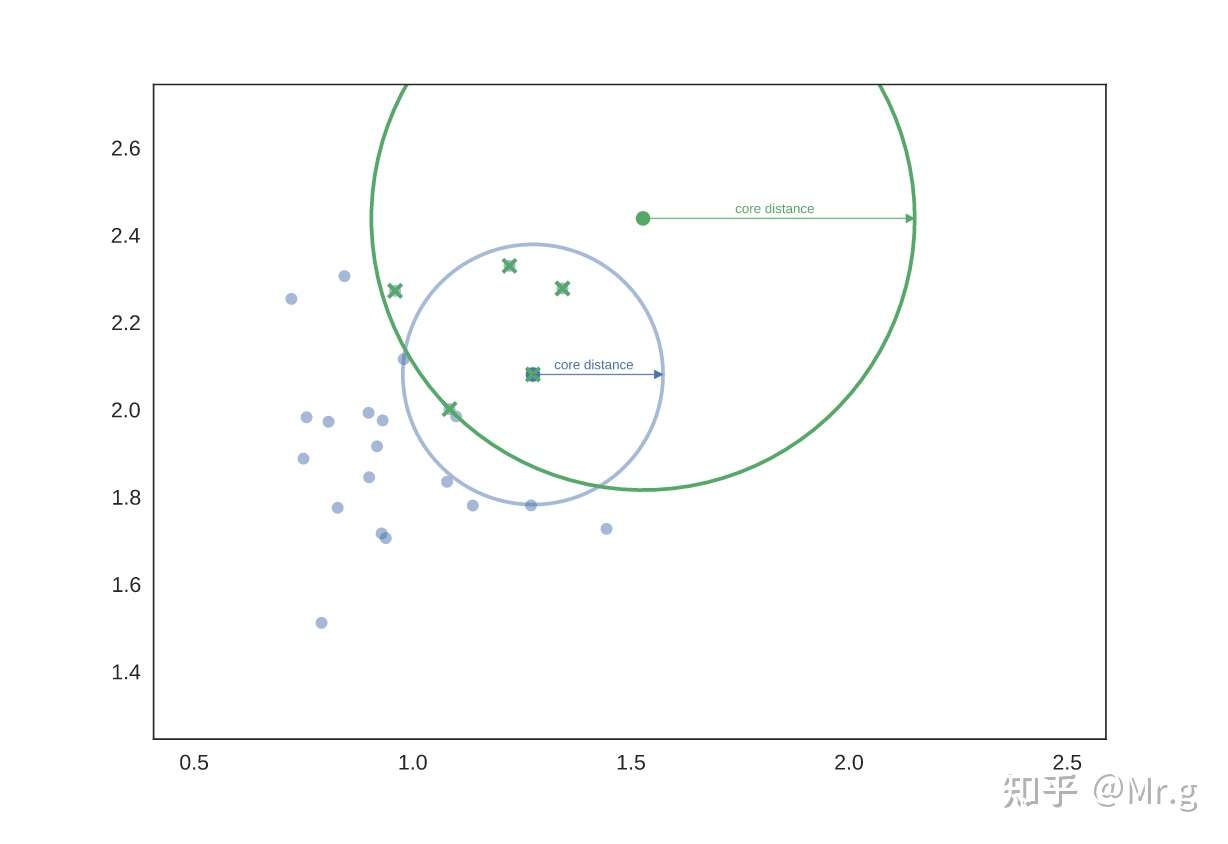
我们再选一个点再做一遍，得到第三组临近点。

img

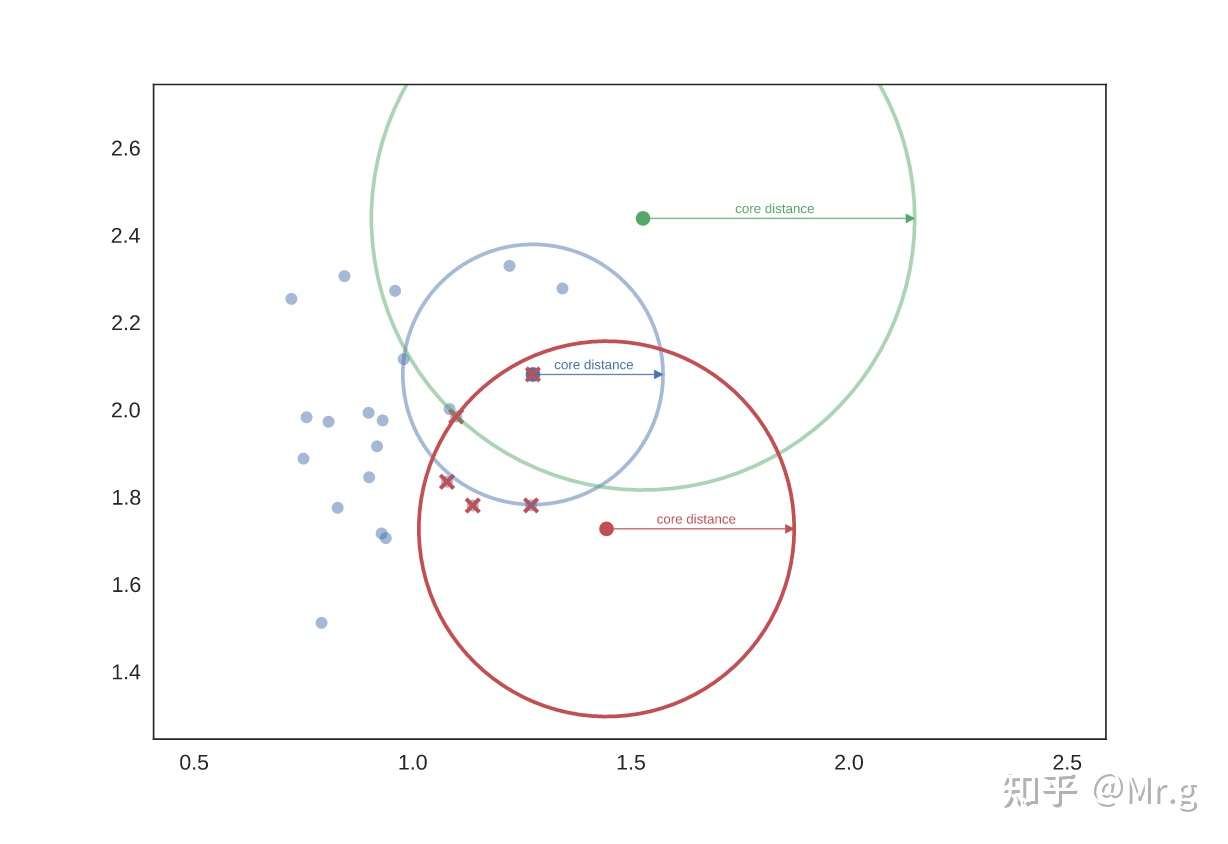
如果我们现在想知道蓝绿两组之间的相互可达距离，我们可以像下图，先画一个箭头连接蓝绿两个圆心：它穿过蓝色圆心，但不穿过绿色圆圈——绿色的核心距离大于蓝色和绿色之间的距离。因此，我们认为蓝色和绿色之间的相互可达距离更大——也就是绿色圆圈的半径（如果我们将一端设在绿色点上，则最容易想象）。

实际上，有基础理论可以证明相互可达距离作为一种变换，在允许单链接聚类的情况下，更接近层次水平上的真实密度分布。

1.2 构建最小生成树

为了从密集的数据集上找到“岛屿”，现在我们有了新的指标：相互可达性。当然密集区是相对的，不同的“岛屿”可能会有不同的密度。 理论上，我们要做的是：将数据当成是一个加权图，以数据点作为顶点，任意两点之间的边的权重等于这些点的相互可达距离。

现在考虑一个阈值，一开始很高，然后逐渐变小。丢弃权重高于该阈值的任何边。我们删除边的同时，连接的组件从图里断开。最终，我们将拥有不同阈值级别的连接元件（从完全连接到完全断开）的层次结构。

实际当中，这样操纵非常耗时：有 n^2 条边，我们不想多次计算连通组件算法。正确的做法是找到最小的边集，从这个集合中删除任何边都会导致组件的连接断开。但是我们还需要找到更多这样的边，使得找不到更小的边来连接组件。幸运的是，图论为我们提供了这样的东西：图的最小生成树。

我们可以通过 Prim 的算法非常有效地构建最小生成树——我们一次构建一条边，每次都把当前最小权重的边去连接一个尚未加入到树中的节点。可以看到下面HDBSCAN构造的树 ；请注意，这是相互可达距离的最小生成树，与图中的纯距离不同。在这种情况下，我们的 k 值为 5。 在这个例子中，存在一种更快的方法，例如用 Dual Tree Boruvka 来构建最小生成树。

1
2
3
4
clusterer.minimum_spanning_tree_.plot(edge_cmap='viridis', 
                                      edge_alpha=0.6, 
                                      node_size=80, 
                                      edge_linewidth=2)

img

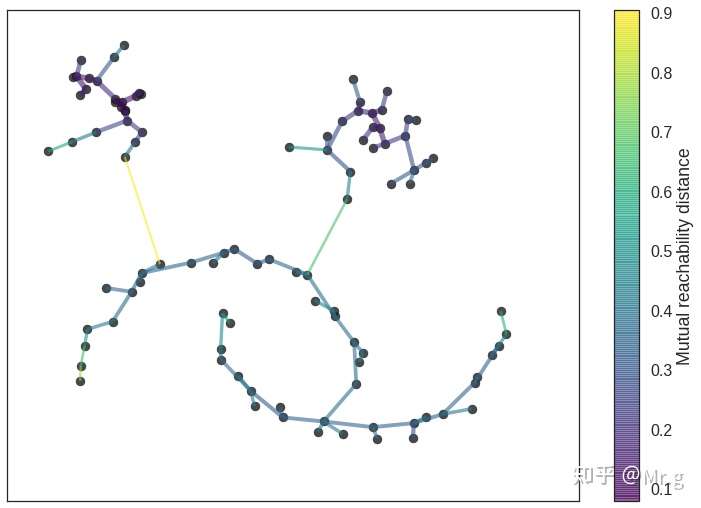
1.3 构建层次聚类

给定最小生成树，下一步是将其转换为层次结构的组件。这最容易以相反的顺序完成：按距离（按递增顺序）对树的边进行排序，然后迭代，为每条边新建一个合并后的簇。这里唯一困难是识别每条边将连接在哪两个簇上，但这通过联合查找数据结构很容易。我们可以将结果视为树状图，如下所示：

img

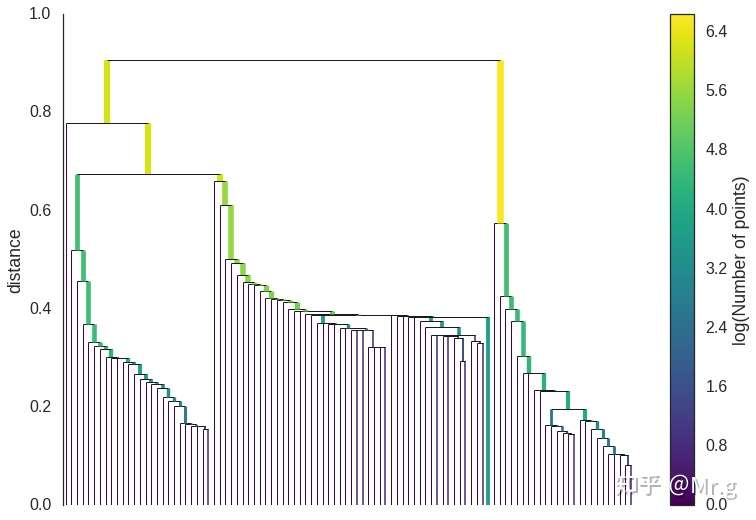
这图可以告诉我们这个鲁棒的单一链接会在哪挺下来。我们想知道；层次结构结构的聚类虽好，但我们想要的是一个扁平的聚类。我们可以通过在上图中画一条水平线并选择它穿过的聚类，来做到这一点。这实际上是 DBSCAN 里用到的操作（将只能切割成单一集群的作为噪声）。问题是，我们怎么知道在哪里画这条线？ DBSCAN 只是把它作为一个（非常不直观的）参数。

更糟糕的是，我们真的要用来处理可变密度的聚类，并希望任何切割线都是通过相互可达距离选出来的，并且今后固定在一个密度水平上。理想情况下，我们希望能够在不同的地方切割树，来选择我们的聚类。这是 HDBSCAN 下一步开始的地方，并与鲁棒的单一链接产生差异。

1.4 压缩聚类树

压缩聚类的第一步是将庞大而复杂的聚类层次结构压缩成一个较小的树，每个节点附加更多的数据。正如您在上面的层次结构中看到的那样，簇分裂通常是从一个簇中分离出一个或两个点；这就是关键点——与其将其视为一个聚类分裂成两个新聚类，不如将其视为一个“有损”的单个持久聚类。

为了具体化，我们需要一个最小簇大小的概念，作为 HDBSCAN 的参数。一旦我们有了最小簇大小的值，我们现在可以遍历层次结构，并在每次拆分时询问拆分创建的新簇之一是否比最小簇大小少。如果我们的点数少于最小簇大小，我们将其声明为“离群点”，并让较大的簇保留父级的簇标识，标记哪些点“离群” ，以及需要的距离值。另一方面，如果要分裂成两个簇，每个簇至少与最小簇大小一样大才能进行分割。

在遍历整个层次结构并执行此操作后，我们最终得到了一个更小节点的树，每个节点都有关于该节点处的簇大小如何随距离变化而减小的数据。我们可以将其可视化为类似于上面的树状图——同样，我们可以让线的宽度代表簇中的点数。对于我们使用最小簇大小 5 的数据，结果如下所示：

1
clusterer.condensed_tree_.plot()

img

这更容易观察和处理，尤其像我们当前测试数据一样简单的时候。然而，我们仍然需要挑出选聚类来用作平面聚类。上面的图应该会给你启发。

1.5 聚类抽取

直觉上, 我们希望选择的簇持久且具有更长的生命周期; 短暂的簇最终可能只是单一链接方法的产 物。可以再看看之前的图, 我们可以说, 我们想要选择图中具有最大墨水面积的那些簇。为了进行 平面聚类, 我们需要添加进一步的要求：即如果您选择了一个簇, 则您不能选择它的任何它子簇。 当然我们需要明确下HDBSCAN实际的算法。首先, 我们需要将它转成一个具体的算法。首先, 我 们需要一个与距离不同的度量来衡量簇的持久性;

我们定义 \(\lambda=\frac{1}{\text { distance }}\) 。对于给定的簇, 我们可 以定义值 \(\lambda_{b i r t h}\) and \(\lambda_{\text {death }}\) 分别是对应笶分裂并成为自己的笟时的 \(\lambda\) ，以及簇分裂成更小的簇时的 \(\lambda\) 值 (如果有）。反过来, 对于给定的簇, 对于该簇中的每个点 \(\mathrm{p}\), 我们可以将值 \(\lambda_p\) 定义为该点“离 群"的 lambda 值, 这是一个介于 \(\lambda_{b i r t h}\) 和 \(\lambda_{\text {death }}\) 之间的值, 因为离群点要么在簇生命周期的某个 时刻离开簇, 或者在簇分裂成两个较小的簇时离开簇。现在, 对于每个簇计算稳定性为 \[ \sum_{p \in \text { cluster }}\left(\lambda_p-\lambda_{\text {birth }}\right) \] 将所有叶节点声明为选定的簇。现在遍历树（反向拓扑排序）。如果子簇的稳定性之和大于笶的稳 定性, 那么我们将簇的稳定性设置为子笶的稳定性之和。另一方面, 如果簇的稳定性大于其子笶的 总和, 则我们将簇固定为一个簇, 并取消选择其所有子簇。一旦我们到达根节点, 我们将当前选定 的簇集称为我们的平面聚类并返回它。

好的, 解析了这么多, 但它实际上只是根据前面我们提到的“选择图中总墨水面积最大的簇"规则来 进行选择。我们可以通过这个算法在压缩树树图中选择簇, 最终会的到你想要的:

1
clusterer.condensed_tree_.plot(select_clusters=True, selection_palette=sns.color_palette())

现在我们有了聚类, 用 sklearn API 可以很容易给每个簇打上标签。任何不在所选聚类中的点都只是一个噪声点（标为 -1）。不过, 我们可以做更多：对于每个簇, 我们有该笶中每个点 \(p\) 的 \(\lambda \_p\) 值; 如果我们简单地将这些值归一化（它们的取值范围从 0 到 1），那么我们就可以衡量簇中每个 点的属于该笶的概率。

hdbscan 库将此作为分类对象的probabilities_属性返回。有了标签和对应的概率，我们就可以画个图, 不同的颜色代表不同的分类, 并根据概率大小降低该颜色的饱和度 （离群的点为纯灰色）。

img

这就是 HDBSCAN 的工作原理。这可能看起来有些复杂——算法有相当多的部分——但实际上每个部分都非常简单，并可以容易掌握。

参考文献

  1. 图解HDBSCANS - Mr.g的文章 - 知乎 https://zhuanlan.zhihu.com/p/412918565
  2. 原文: How HDBSCAN works
  3. 聚类算法(Clustering Algorithms)之层次聚类(Hierarchical Clustering) - 小玉的文章 - 知乎 https://zhuanlan.zhihu.com/p/363879425