理论基础(2)激活函数
一、激活函数
激活函数简述激活函数是向神经网络中引入非线性因素,通过激活函数神经网络就可以拟合各种曲线。激活函数主要分为饱和激活函数(Saturated Neurons)和非饱和函数(One-sided Saturations)。Sigmoid和Tanh是饱和激活函数,而ReLU以及其变种为非饱和激活函数。非饱和激活函数主要有如下优势:
- 非饱和激活函数可以解决梯度消失问题。
- 非饱和激活函数可以加速收敛。

1.1 梯度消失(Vanishing Gradients)
Sigmoid的函数图像和Sigmoid的梯度函数图像分别为(a)、(e),从图像可以看出,函数两个边缘的梯度约为0,梯度的取值范围为(0,0.25)。求解方程为:
\[ \begin{gathered}y=1 /\left(1+e^{-x}\right) \\ y^{\prime}=y(1-y)\end{gathered} \]
- Sigmoid极容易导致梯度消失问题。饱和神经元会使得梯度消失问题雪上加霜,假设神经元输入Sigmoid的值特别大或特别小,对应的梯度约等于0,即使从上一步传导来的梯度较大,该神经元权重(w)和偏置(bias)的梯度也会趋近于0,导致参数无法得到有效更新。
- 计算费时。 在神经网络训练中,常常要计算Sigmid的值进行幂计算会导致耗时增加。
- Sigmoid函数不是关于原点中心对称的(zero-centered),Tanh激活函数解决了原点中心对称问题。
1.2 ReLU与死亡神经元
(1) ReLU解决梯度消失问题
ReLU激活函数的提出就是为了解决梯度消失问题。ReLU的梯度只可以取两个值:0或1,当输入小于0时,梯度为0;当输入大于0时,梯度为1。好处就是:ReLU的梯度的连乘不会收敛到0,连乘的结果也只可以取两个值:0或1 。如果值为1,梯度保持值不变进行前向传播;如果值为0 ,梯度从该位置停止前向传播。
- Sigmoid函数是双侧饱和的,即朝着正负两个方向函数值都会饱和;
- ReLU函数是单侧饱和的,即只有朝着负方向,函数值才会饱和。严格意义上来说,将ReLU函数值为0的部分称作饱和是不正确的(饱和应该是取值趋近于0),但效果和饱和是一样的。
假设神经元为检测某种特定特征的开关,高层神经元负责检测高级的/抽象的特征(有着更丰富的语义信息),例如眼睛或者轮胎;低层神经元负责检测低级的/具象的特征(曲线或者边缘)。当开关处于开启状态,说明在输入范围内检测到了对应的特征,且正值越大代表特征越明显。加入某个神经元负责检测边缘,则正值越大代表边缘区分越明显(sharp)。假设一个负责检测边缘的神经元,激活值为1相对于激活值为0.5来说,检测到的边缘区分地更明显;但激活值-1相对于-0.5来说就没有意义了,因为低于0的激活值都代表没有检测到边缘。所以用一个常量值0来表示检测不到特征是更为合理的,像ReLU这样单侧饱和的神经元就满足要求。
单侧饱和还能使得神经元对于噪声干扰更具鲁棒性。假设一个双侧都不饱和的神经元,正侧的不饱和导致神经元正值的取值各不相同,这是所希望的,因为正值的大小代表了检测特征信号的强弱。但负值的大小引入了背景噪声或者其他特征信息,这会给后续的神经元带来无用的干扰且可能导致神经元之间的相关性,相关性是容易造成模型病态的。例如检测直线的神经元和检测曲线的神经元可能有负相关性。在负值区域单侧饱和的神经元则不会有上述问题,噪声的程度大小被饱和区域都截断为0,避免了无用信息的干扰。
使用ReLU激活函数在计算上也是高效的。相对于Sigmoid函数梯度的计算,ReLU函数梯度取值只有0或1。且ReLU将负值截断为0 ,为网络引入了稀疏性,进一步提升了计算高效性。
1.3 神经元死亡
ReLU尽管稀疏性可以提升计算高效性,但同样也可能阻碍训练过程。通常,激活函数的输入值有一偏置项(bias),假设bias变得太小,以至于输入激活函数的值总是负的,那么反向传播过程经过该处的梯度恒为0,对应的权重和偏置参数此次无法得到更新。如果对于所有的样本输入,该激活函数的输入都是负的,那么该神经元再也无法学习,称为神经元”死亡“问题。
(1) Leaky ReLU可以解决神经元”死亡“问题
Leaky ReLU的提出就是为了解决神经元”死亡“问题,Leaky ReLU与ReLU很相似,仅在输入小于0的部分有差别,ReLU输入小于0的部分值都为0,而LeakyReLU输入小于0的部分,值为负,且有微小的梯度。函数图像为(d)。
使用Leaky ReLU的好处就是:在反向传播过程中,对于Leaky ReLU激活函数输入小于零的部分,也可以计算得到梯度(而不是像ReLU一样值为0),这样就避免了梯度方向锯齿问题。
α的分布满足均值为0,标准差为1的正态分布,该方法叫做随机Leaky ReLU(Randomized Leaky ReLU)。原论文指出随机Leaky ReLU相比Leaky ReLU能得更好的结果,且给出了参数α的经验值1/5.5(好于0.01)。至于为什么随机Leaky ReLU能取得更好的结果,解释之一就是随机Leaky ReLU小于0部分的随机梯度,为优化方法引入了随机性,这些随机噪声可以帮助参数取值跳出局部最优和鞍点。将α作为了需要学习的参数,该激活函数为PReLU(Parametrized ReLU)。
1.4 ELU(Exponential Linear Unit)
理想的激活函数应满足两个条件:
- 输出的分布是零均值的,可以加快训练速度。
- 激活函数是单侧饱和的,可以更好的收敛。
LeakyReLU和PReLU满足第1个条件,不满足第2个条件;而ReLU满足第2个条件,不满足第1个条件。两个条件都满足的激活函数为ELU(Exponential Linear Unit),函数图像如图(e)。其表达式如下:
\[ f(x)= \begin{cases}x, & x>0 . \\ \alpha\left(e^x-1\right), & x \leq 0 .\end{cases} \]
1.5 梯度爆炸
梯度误差是在神经网络训练期间计算的方向和梯度,神经网络以正确的方向和数值更新网络权重。在深度网络或递归神经网络中,梯度误差可能在更新过程中累积,造成非常大的梯度。这反过来会导致网络权重的大量更新,进而导致网络不稳定。在极端情况下,权重值可能变得太大,以至于溢出并导致NaN值现成梯度爆炸现象。
梯度爆炸是通过指数增长发生的,通过在网络层(其值大于1.0)中重复乘以梯度。
梯度爆炸现象:模型无法“加入”训练数据,比如损失函数很差;模型不稳定,每次更新的损失变化很大;模型损失在训练过程中变为NaN
如何解决梯度爆炸?
1.重现设计神经网络,减少网络层数、减小batch szie、截断。
2.使用LSTM
3.使用梯度裁剪、clipnorm=1.0 clipvalue=0.5
4.使用权重正则L1 & L2
二、常用激活函数
常用的激活函数:sigmoid,Tanh,ReLU,Leaky ReLU,PReLU,ELU,Maxout
2.1 sigmoid函数
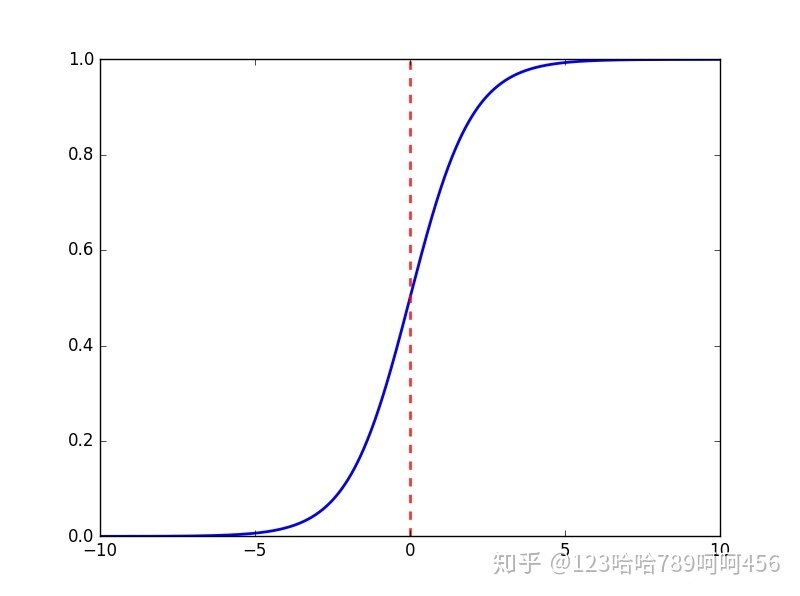
sigmoid函数又称 Logistic函数,用于隐层神经元输出,取值范围为(0,1),可以用来做二分类。
表达式: \[ $\sigma(x)=\frac{1}{1+e^{-x}}$ \]
导数为: \[
\sigma^{\prime}(x)=\sigma(x)[1-\sigma(x)]
\]
优点:
- Sigmoid函数的输出在(0,1)之间,输出范围有限,优化稳定,可以用作输出层。
- 线性回归在实数域上敏感度一致,而逻辑回归在 0 附近敏感,在远离 0 点位置不敏感,这个的好处就是模型更加关注分类边界,可以增加模型的鲁棒性。
- 连续函数,便于求导。
缺点:
- sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象,意味着函数会变得很平,并且对输入的微小改变会变得不敏感。【梯度消失】
- sigmoid函数的输出不是0均值的,会导致后层的神经元的输入是非0均值的信号,这会对梯度产生影响。具体可参考下面,简单说就是可能导致收敛效率低的问题;
- 计算复杂度高,因为sigmoid函数是指数形式。
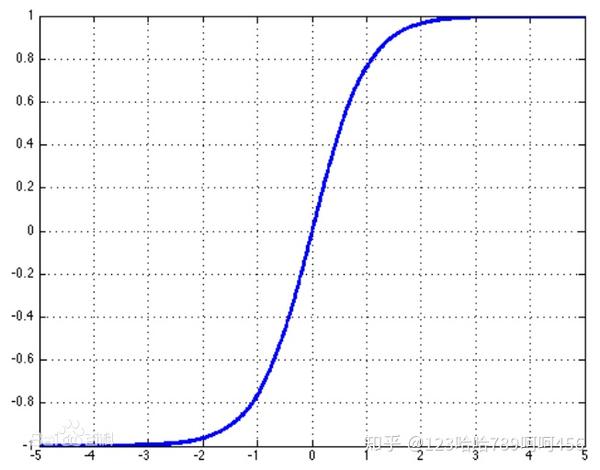
2.2 Tanh函数
Tanh函数也称为双曲正切函数,取值范围为[-1,1]。Tanh函数是 0 均值的,因此实际应用中 Tanh 会比 sigmoid 更好。但是仍然存在梯度饱和与exp计算复杂度高的问题。
Tanh函数定义如下: \[
f(x)=\operatorname{Tanh} x=\frac{\sinh x}{\cosh
x}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
\] 它的导数为: \[
f^{\prime}(x)=1-[f(x)]^{2}
\]
2.3 ReLU函数
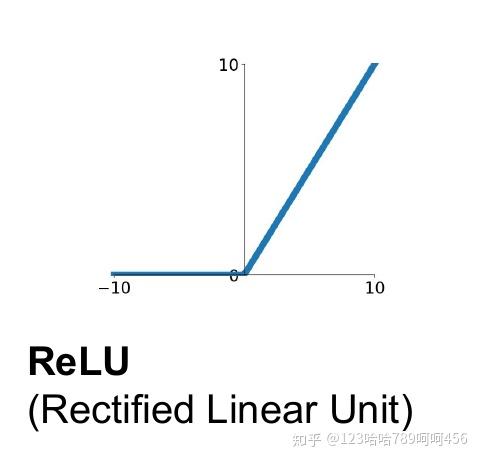
整流线性单元 (Rectified linear unit, ReLU) 是现代神经网络中最常用的激活函数, 大多数 前馈神经网络默认使用的激活函数。
ReLU函数定义如下: \(\quad f(x)=\max (0, x)\)
优点:
- 使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。
- 在 \(x>0\) 区域上, 不会出现梯度饱和、梯度消失的问题。
- 计算复杂度低, 不需要进行指数运算, 只要一个阈值就可以得到激活值。
缺点:
- ReLU的输出不是O均值的。
- Dead ReLU Problem(神经元坏死现象):ReLU在负数区域被kill的现象叫做dead relu。 ReLU在训练的时很“脆弱”。在 \(x<0\) 时, 梯度为 0 。这个神经元及之后的神经元梯度永远为 0 ;产生这种现象的两个原因:参数初始化问题;learning rate太高导致在训练过程中参数更新太大。
三、激活函数
2.1 在神经网络中,激活函数sigmoid和tanh除了阈值取值外有什么不同吗?
2.2 了解那些激活函数以及应用?
回答主要分两类(饱和/非饱和),以及应用场景等。有时候可能特定到具体经典模型,比如LSTM用到Tanh,Transfromer中用到的ReLU,Bert中的GeLU,YOLO的Leaky ReLU等。
2.3 梯度消失与梯度爆炸现象与原因以及解决办法?
2.4 ReLU激活函数为什么会出现死神经元,解决办法?
输入为负值时,ReLU的梯度为0造成神经元死亡。还有Learning rate太高导致在训练过程中参数更新太大 。
解决办法主要有:
- 优化参数。
- 避免将learning rate设置太大,或者使用Adam等自动调节learning rate的方法。
- 更换激活函数。
参考文献
深度学习领域最常用的10个激活函数,一文详解数学原理及优缺点 - 机器之心的文章 - 知乎 https://zhuanlan.zhihu.com/p/352668984
详解激活函数(Sigmoid/Tanh/ReLU/Leaky ReLu等) - 李见黎的文章 - 知乎 https://zhuanlan.zhihu.com/p/427541517