Pytorch（11）模型训练-优化器

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 4 分钟

[PyTorch 学习笔记] 优化器

torch.optim.lr_scheduler：调整学习率：https://blog.csdn.net/qyhaill/article/details/103043637

这篇文章主要介绍了 PyTorch 中的优化器，包括 3 个部分：优化器的概念、optimizer 的属性、optimizer 的方法。

一、优化器

1.1 优化器的概念

PyTorch 中的优化器是用于管理并更新模型中可学习参数的值，使得模型输出更加接近真实标签。

1.2 optimizer 的属性

PyTorch 中提供了 Optimizer 类，定义如下：

1
2
3
4
5
class Optimizer(object):
 def __init__(self, params, defaults):
        self.defaults = defaults
        self.state = defaultdict(dict)
        self.param_groups = [] # momentum、lr、weight_decay、params 等。

主要有 3 个属性

  • defaults：优化器的超参数，如 weight_decay，momentum
  • state：参数的缓存，如 momentum 中需要用到前几次的梯度，就缓存在这个变量中
  • param_groups：管理的参数组，是一个 list，其中每个元素是字典，包括 momentum、lr、weight_decay、params 等。
  • _step_count：记录更新 次数，在学习率调整中使用

1.3 optimizer 的方法

  • zero_grad()：清空所管理参数的梯度。由于 PyTorch 的特性是张量的梯度不自动清零，因此每次反向传播之后都需要清空梯度。
  • step()：执行一步梯度更新
  • add_param_group()：添加参数组
  • state_dict()：获取优化器当前状态信息字典
  • load_state_dict()：加载状态信息字典，包括 state 、momentum_buffer 和 param_groups。主要用于模型的断点续训练。我们可以在每隔 50 个 epoch 就保存模型的 state_dict 到硬盘，在意外终止训练时，可以继续加载上次保存的状态，继续训练。

1.4 学习率

学习率是影响损失函数收敛的重要因素，控制了梯度下降更新的步伐。下面构造一个损失函数 [公式]，[公式] 的初始值为 2，学习率设置为 1。

1.5 momentum 动量

在 PyTroch 中，momentum 的更新公式是：

[公式]
[公式]

==momentum 动量的更新方法，不仅考虑当前的梯度，还会结合前面的梯度。==

momentum 来源于指数加权平均：[公式]，其中 [公式] 是上一个时刻的指数加权平均，[公式] 表示当前时刻的值，[公式] 是系数，一般小于 1。指数加权平均常用于时间序列求平均值。假设现在求得是 100 个时刻的指数加权平均，那么

[公式] [公式] [公式]

[公式]

从上式可以看到，由于 [公式] 小于 1，越前面时刻的 [公式]，[公式] 的次方就越大，系数就越小。

[公式] ==可以理解为记忆周期，[公式] 越小，记忆周期越短，[公式] 越大，记忆周期越长==。通常 [公式] 设置为 0.9，那么 [公式]，表示更关注最近 10 天的数据。

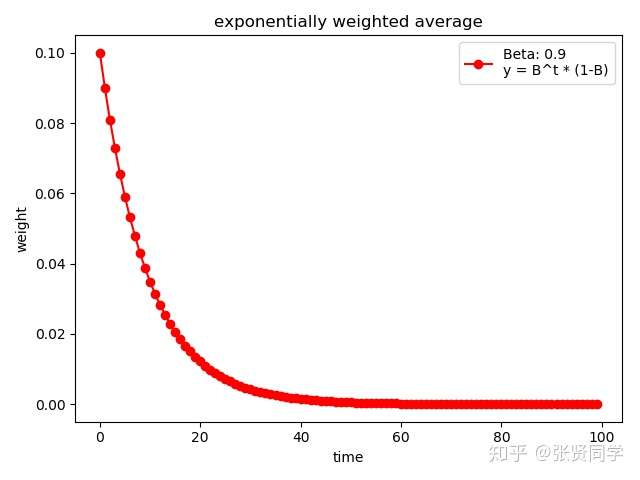
下面代码展示了 [公式] 的情况

1
2
3
4
5
6
7
8
9
10
weights = exp_w_func(beta, time_list)

    plt.plot(time_list, weights, '-ro', label="Beta: {}\ny = B^t * (1-B)".format(beta))
    plt.xlabel("time")
    plt.ylabel("weight")
    plt.legend()
    plt.title("exponentially weighted average")
    plt.show()

    print(np.sum(weights))

结果为：

img

下面代码展示了不同的 [公式] 取值情况

1
2
3
4
5
6
7
8
beta_list = [0.98, 0.95, 0.9, 0.8]
w_list = [exp_w_func(beta, time_list) for beta in beta_list]
for i, w in enumerate(w_list):
    plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
    plt.xlabel("time")
    plt.ylabel("weight")
plt.legend()
plt.show()

结果为：

img

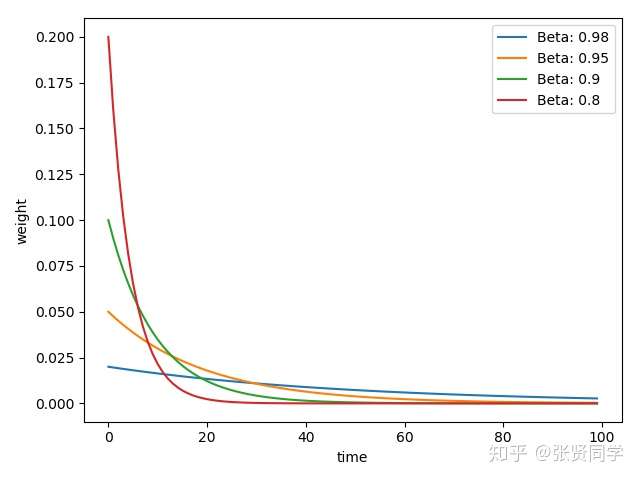
[公式] ==的值越大，记忆周期越长，就会更多考虑前面时刻的数值，因此越平缓。==

二、常用优化器

2.1 ==optim.SGD==：随机梯度下降法

1
optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False

主要参数：

  • params：管理的参数组
  • lr：初始学习率
  • momentum：动量系数 [公式]
  • weight_decay：L2 正则化系数
  • nesterov：是否采用 NAG

2.2 ==optim.Adagrad==：自适应学习率梯度下降法

2.3 optim.RMSprop ：Adagrad 的改进

2.4 optim.Adadelta

2.5 ==optim.Adam==：RMSProp 集合 Momentum，这个是目前最常用的优化器，因为它可以使用较大的初始学习率。

2.6 optim.Adamax：Adam 增加学习率上限

#### optim.SparseAdam：稀疏版的 Adam

#### optim.ASGD：随机平均梯度下降

#### optim.Rprop：弹性反向传播，这种优化器通常是在所有样本都一起训练，也就是 batchsize 为全部样本时使用。

#### optim.LBFGS：BFGS 在内存上的改进