理论基础(4)Dropout
为什么dropout 可以解决过拟合? 【共享隐藏单元的bagging集成模型】
集成取平均的作用: 整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
减少神经元之间复杂的共适应关系: 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
Dropout纯粹作为一种高效近似Bagging的方法。然而,有比这更进一步的Dropout观点。 Dropout不仅仅是训练一个Bagging的集成模型,并且是共享隐藏单元的集成模型。这意味着无论其他隐藏单元是否在模型中,每个隐藏单元必须都能够表现良好。
一、Dropout
1.1 Dropout简介
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
(1)容易过拟合
(2)费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
1.2 Dropout原理
在2012年,Hinton在其论文《Improving neural networks by preventing co-adaptation of feature detectors》中提出Dropout。当一个复杂的前馈神经网络被训练在小的数据集时,容易造成过拟合。为了防止过拟合,可以通过阻止特征检测器的共同作用来提高神经网络的性能。
在2012年,Alex、Hinton在其论文《ImageNet Classification with Deep Convolutional Neural Networks》中用到了Dropout算法,用于防止过拟合。并且,这篇论文提到的AlexNet网络模型引爆了神经网络应用热潮,并赢得了2012年图像识别大赛冠军,使得CNN成为图像分类上的核心算法模型。
随后,又有一些关于Dropout的文章《Dropout:A Simple Way to Prevent Neural Networks from Overfitting》、《Improving Neural Networks with Dropout》、《Dropout as data augmentation》。
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
Dropout说的简单一点就是:我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征。
Dropout 是另一种抑制过拟合的方法。在使用 dropout 时,数据尺度会发生变化,如果设置 dropout_prob =0.3,那么在训练时,数据尺度会变为原来的 70%; 而在测试时,执行了 model.eval() 后,dropout 是关闭的,因此所有权重需要乘以 (1-dropout_prob),把数据尺度也缩放到 70%。 加了 dropout 之后,权值更加集中在 0 附近,使得神经元之间的依赖性不至于过大。
PyTorch 中 Dropout 层如下,通常放在每个网路层的最前面:
1 | torch.nn.Dropout(p=0.5, inplace=False) |
参数:
- p:主力需要注意的是,p 是被舍弃的概率,也叫失活概率;代码层面实现让某个神经元以概率p停止工作,其实就是让它的激活函数值以概率p变为0
1.3 Dropout具体工作流程
- 首先随机(临时)删掉网络中一部分的隐藏神经元,输入输出神经元保持不变;
- 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
- 恢复被删掉的神经元( 此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 重复上述过程
(1)训练阶段
- 无可避免的,在训练网络的每个单元都要添加一道概率流程。
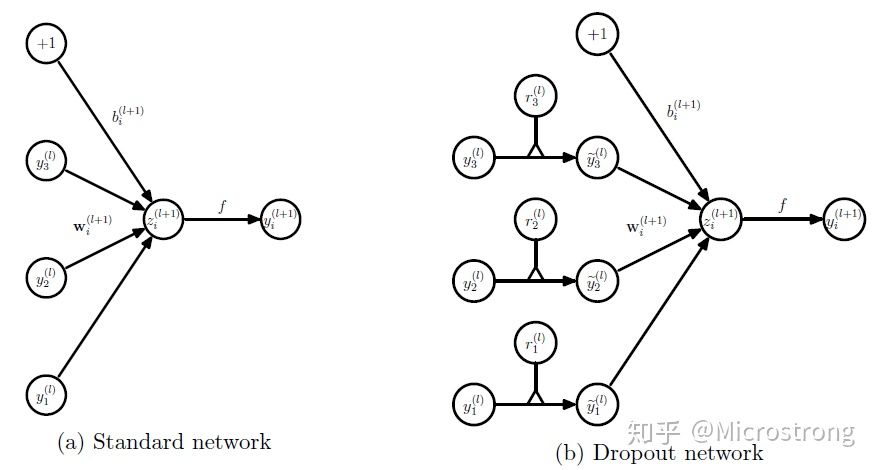
对应的公式变化如下: - 没有Dropout的网络计算公式 \[ \begin{aligned} z_{i}^{(l+1)} &=\mathbf{w}_{i}^{(l+1)} \mathbf{y}^{l}+b_{i}^{(l+1)} \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) \end{aligned} \] - 采用Dropout的网络计算公式 \[ \begin{aligned} r_{j}^{(l)} & \sim \operatorname{Bernoulli}(p), \\ \widetilde{\mathbf{y}}^{(l)} &=\mathbf{r}^{(l)} * \mathbf{y}^{(l)}, \\ z_{i}^{(l+1)} &=\mathbf{w}_{i}^{(l+1)} \widetilde{\mathbf{y}}^{l}+b_{i}^{(l+1)}, \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) . \end{aligned} \] 上面公式中Bernoulli函数是为了生成概率r向量, 也就是随机生成一个0、1的向量。
代码层面实现让某个神经元以概率 \(p\) 停止工作, 其实就是让它的激活函数值以概率 \(p\) 变为 0 。比如我们某一层网络神经元的个数为 1000 个, 其激活函数输出值为 \(y 1 、 y 2 、 y 3 、 \ldots \ldots, y 1000\), 我们 dropout比率选择0.4, 那么这一层神经元经过dropout后, 1000个神经元中会有大约400个的值被置为 0 。
注意: 经过上面屏蔽掉某些神经元, 使其激活值为 0 以后, 我们还需要对向量y1.......y1000进行缩放, 也就是乘以 \(1 /(1-p)\) 。如果你在训练的时候, 经过置0后, 没有对y1......y1000进行缩放 (rescale) , 那么在测试的时候, 就需要对权重进行缩放, 操作如下。
(2)测试阶段
预测模型的时候, 每一个神经单元的权重参数要乘以概率p。
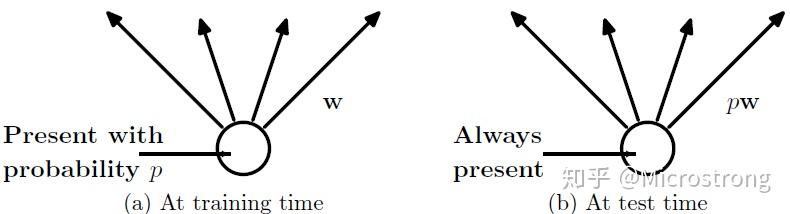
测试阶段Dropout公式: \[ w_{\text {test }}^{(l)}=p W^{(l)} \]
1.4 为什么dropout 可以解决过拟合? 【共享隐藏单元的bagging集成模型】
集成取平均的作用: 整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
减少神经元之间复杂的共适应关系: 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
Dropout纯粹作为一种高效近似Bagging的方法。然而,有比这更进一步的Dropout观点。 Dropout不仅仅是训练一个Bagging的集成模型,并且是共享隐藏单元的集成模型。这意味着无论其他隐藏单元是否在模型中,每个隐藏单元必须都能够表现良好。
面试常见问题-dropout与bagging的区别
- dropout训练与bagging训练不太一样,bagging的各个子模型之间是完全独立的,而在dropout里,这些参数是共享的。
- 在bagging的情况下,每一个模型在其训练集上训练到收敛,而在dropout情况下,通常大部分的模型都没有显式的训练
1.5 model.eval() 和 model.trian()
有些网络层在训练状态和测试状态是不一样的,如 dropout 层,在训练时
dropout
层是有效的,但是数据尺度会缩放,为了保持数据尺度不变,所有的权重需要除以
1-p。而在测试时 dropout
层是关闭的。因此在测试时需要先调用model.eval()设置各个网络层的的training属性为
False,在训练时需要先调用model.train()设置各个网络层的的training属性为
True。
参考文献
- 深度学习中Dropout原理解析 - Microstrong的文章 - 知乎 https://zhuanlan.zhihu.com/p/38200980