风控算法(2)风控模型-抽样对Lift和KS指标的影响
风控模型
风控业务背景
在测试外部三方数据时,数据服务商只允许我们抛出有限一定量样本(例如5w、10w、20w)来匹配三方数据。这就要求我们对样本抽样。在对外部数据建模测算后,我们如何将结果还原到原始样本上评估呢?针对这种常见场景,本文将探索抽样对lift指标和KS指标的影响。
一、样本抽样方法
在《外部数据风控建模评估分析》中,我们介绍过外部数据的一些基本知识,其测算流程大致如图1所示。
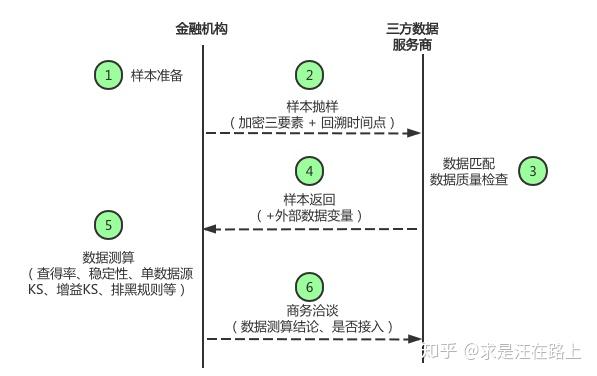
在测算外部数据前,第一步非常重要,样本是我们一切分析的载体。由于三方数据服务商一般只能提供有限的测试量(比如10w),那么我们只能从业务样本中进行抽样。那么可以采取哪些抽样方法呢?一般有以下几种:
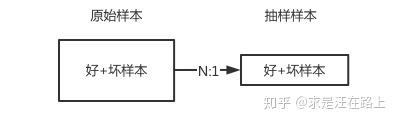
1.1 简单随机抽样,保持内部真实好坏比例。
- 好处:建模时可以直接评估模型效果,而不需要考虑==bad rate==失真。
- 坏处:好坏样本严重不均衡,坏样本总是极少量的,我们可能需要逐月评估单变量和模型KS,以此观察区分度的稳定性。此时,坏样本较少,导致结果失去统计意义,波动较大
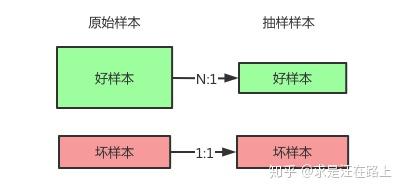
1.2 好坏分层抽样,好样本N:1抽样,坏样本1:1抽样。
比如,假设内部bad rate是5%,也就是好坏比例约为20:1,那么从20个好样本中随机抽1个,坏样本则全部保留。由此,我们在评估真实bad rate捕捉率时,也可以按此权重进行还原。即,1个好样本代表20个原始好样本。
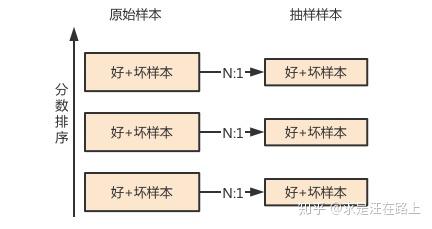
1.3 按资质对客群分层,再分层随机抽样。
具体操作方法为:
- 以某段时间窗的样本训练一个排序模型,例如风险模型(PD),或过退模型(AR)。
- 对这个时间窗外待抽样的样本进行排序,将人群分为若干个分层。
- 分层抽样,每组中相同比例。
这样就可以用来建立适应不同客群的信用分。
这三种方案里,我们最常采用方案二。因此,本文以该方案为例进行探讨。
二、Lift和KS指标介绍
Lift, 名称为提升度, 其含义为:经过某种排序后圈出来的坏人浓度, 相对于随机抽样的坏人浓度的提升, 即: \[ L i f t=\frac{cover-bad-rate}{total-bad-rate} \] 举例说明, 如图5所示, 现在有 50 个人, 其中 5 个坏人, 那么整体坏人占比为 \(10 \%\) 。我们将其随机分为 5 组, 每组 10 人,则理想情况下,每组中有 1 个坏人。
现在我们拥有一个排序模型, 对这 50 个人排序后, 我们笑选出分数最低的 10 个人, 也就是第一组, 此时能抓住 2 个 坏人, 坏人浓度为 \(20 \%\) 。那么 lift \(=20 \% / 10 \%=2\) 。
在反欺诈场景中,我们常会用到Lift这个指标来判断规则的有效性。在测试外部数据时,我们会发现有些变量的区分度虽然很低,或者查得率很低,但是其查得人群的坏人捕捉率却很高。这对我们如何进行规则发现也是一个启发。
KS指标的含义详见:《区分度评估指标(KS)深入理解应用》
三、抽样对Lift指标的影响
现在我们有这样一个场景,在抽样样本上我们制定一个阈值cutoff,高于这个阈值则通过(PS),低于这个阈值则拒绝(RJ)。在抽样样本上,我们测算拒绝部分的坏人lift,那么在原始样本上,相应的lift是多少呢?
我们按照lift的定义来推导所带来的影响。 \[ \begin{aligned} & L i f t=\frac{B a d_{r j} / R J}{\left(B a d_{r j}+B a d_{p s}\right) /(R J+P S)} \\ & =\frac{B a d_{r j}}{R J} \times \frac{R J+P S}{B a d_{r j}+B a d_{p s}} \\ & =\frac{B a d_{r j}}{\operatorname{Bad}_{r j}+\operatorname{Bad}_{p s}} \times \frac{R J+P S}{R J} \\ & =\frac{B a d_{r j}}{B a d_{r j}+B a d_{p s}} \times\left(1+\frac{P S}{R J}\right) \\ & \end{aligned} \] 其中: - \(B a d_{r j}\) : 拒绝部分的真实坏样本数 - \(\operatorname{Good}_{r j}\) : 拒绝部分的真实好样本数 - \(B_{p s}\) :通过部分的真实坏样本数 - \(\operatorname{Good}_{p s}\) : 通过部分的真实好样本数
由于全部保留 \(B a d\) 样本, 同时采用相同的cutoff, 那么 \(B a d_{r j}\) 和 \(B a d_{p s}\) 在抽样前后保持不变。同时, 不可能有 完美的模型, 因此无论是 \(R J\) 还是 \(P S\) 中都有好坏样本,即: \[ \begin{aligned} & R J=B_{a d_{r j}}+\operatorname{Good}_{r j} \\ & P S=\operatorname{Bad}_{p s}+\operatorname{Good}_{p s} \end{aligned} \] 由于简单随机抽样, 假设抽样比例为 rate,那么: \[ \text { Good }_{\text {sample }}=\text { Good }_{\text {origin }} \times \text { rate } \] 同时,在相同的cutoff下,也就是相同的标准下,抽样和原始样本中的好样本比例应该相同,即: \[ \begin{aligned} & \text { Good }_{r j \_} \_ \text {sample }=\text { Good }_{r j \_} \_ \text {origin } \times \text { rate } \\ & \text { Good }_{p s \_} \text {sample }=\text { Good }_{p s \_} \_ \text {origin } \times \text { rate } \\ & \end{aligned}在抽样样本上: \] 在抽样样本上: \[ \begin{aligned} & L i f t_{s a m p l e}=\frac{B a d_{r j}}{B a d_{r j}+B a d_{p s}} \times\left(1+\frac{P S_s}{R J_s}\right) \\ & =\frac{B a d_{r j}}{B a d_{r j}+B a d_{p s}} \times\left(1+\frac{B a d_{p s}+\operatorname{Good}_{p s}}{B a d_{r j}+\operatorname{Good}_{r j}}\right) \end{aligned} \] 在原始样本上: \[ \begin{aligned} & =\frac{B a d_{r j}}{\operatorname{Bad}_{r j}+\text { Bad }_{p s}} \times\left(1+\frac{\text { Bad }_{p s}+\text { Good }_{p s} / \text { rate }}{\operatorname{Bad}_{r j}+\text { Good }_{r j} / \text { rate }}\right) \\ & =\frac{B a d_{r j}}{\operatorname{Bad}_{r j}+\operatorname{Bad}_{p s}} \times\left(1+\frac{\text { rate } \times \operatorname{Bad}_{p s}+\operatorname{Good}_{p s}}{\text { rate } \times \operatorname{Bad}_{r j}+\operatorname{Good}_{r j}}\right) \\ & \end{aligned} \] 对比公式(6)和 (7),我们发现,原始样本上的lift完全可以通过抽样分布上的值进行计算。我们再以实验佐证理论,发现几乎是一样的。造成些许差异的原因可能是样本量。
四、抽样对KS指标的影响
在《区分度评估指标(KS)深入理解应用》中,我们认识了KS的计算原理。那么对于随机抽样而言,好人分布和坏人分布是相互独立的,那么在计算累积好样本分布和累积坏样本分布时,理论上KS不应该发生变化。
数据胜于雄辩。首先对好样本5:1抽样,坏样本则保持1:1不变,由此组成新样本集。
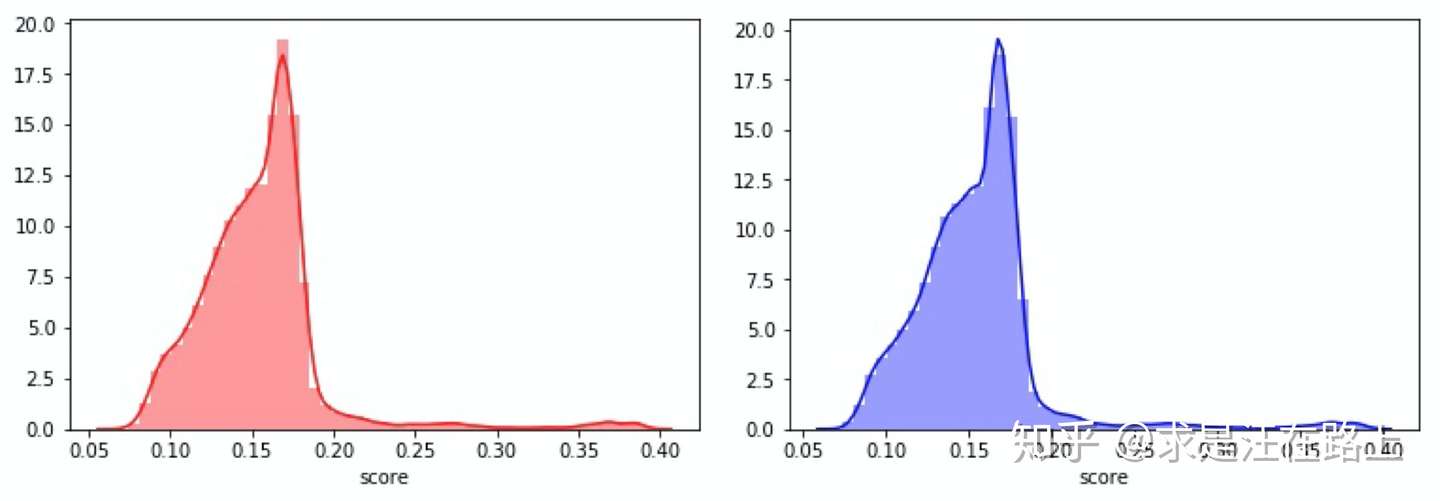
接下来,我们对比抽样前后的KS差异,如图8所示。结果并无明显区别。
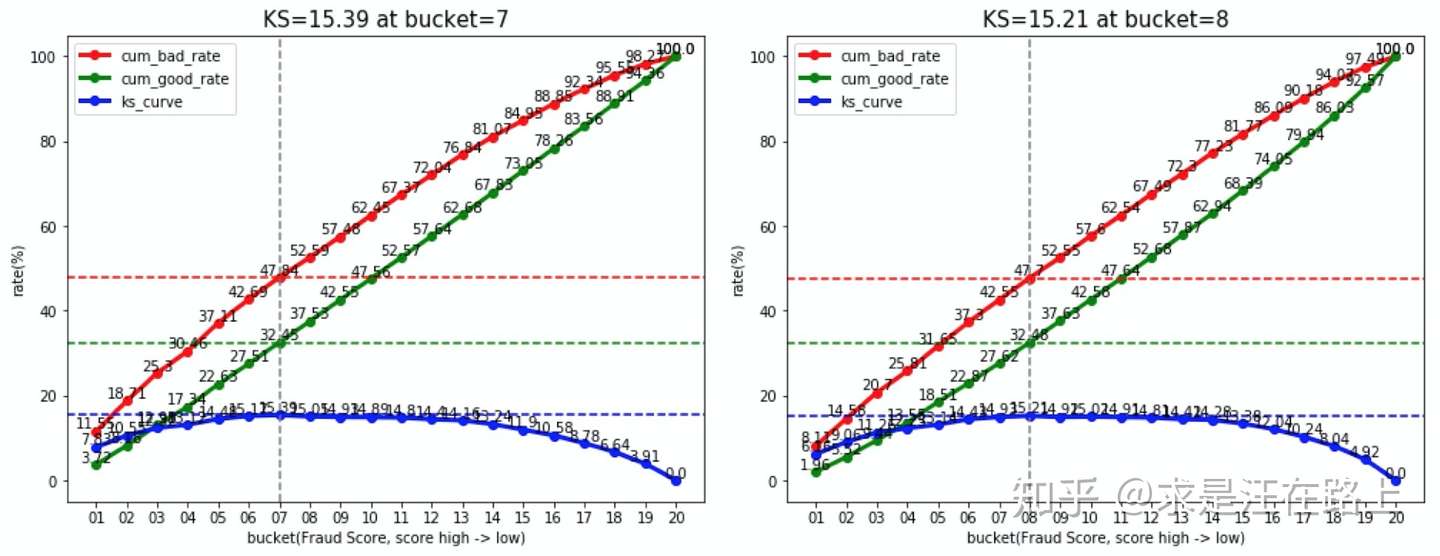
因此,结论为:分层抽样不会改变KS,抽样样本与原始样本上计算的KS相同。在实践中,我们可能因为坏样本过少等原因会影响一些差异,但整体无明显差异。
五、总结
在匹配外部数据后,我们在抽样样本上会进行一些测算,同时希望能还原在真实原始样本上的结果。针对一些模型指标(Lift、KS)的在抽样前后变化情况,结论为:
- lift指标数值将会发生变化,但可以换算得到。
- ks指标不会发生变化,但需要保证样本量足够。