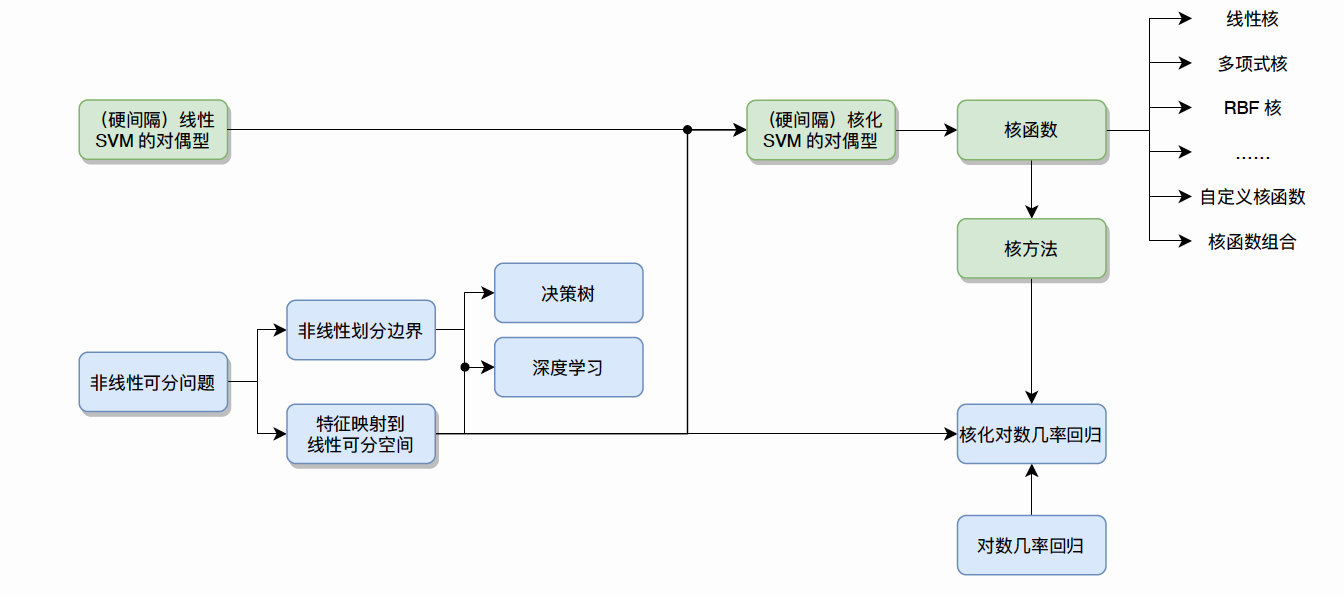
支持向量机(3)核函数
SVM 是一个非常优雅的算法,具有完善的数学理论,虽然如今工业界用到的不多,但还是决定花点时间去写篇文章整理一下。
本质:SVM 想要的就是找到各类样本点到超平面的距离最远,也就是找到最大间隔超平面。为了对数据中的噪声有一定的容忍能力。以几何的角度,在丰富的数据理论的基础上,简化了通常的分类和回归问题。
几何意义:找到一个超平面将特征空间的正负样本分开,最大分隔(对噪音有一定的容忍能力);
间隔表示:划分超平面到属于不同标记的最近样本的距离之和;
一、核函数
1.1 线性不可分
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里,再通过间隔最大化的方式,学习得到支持向量机,就是非线性 SVM。
我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。
但我们可能会碰到的一种情况是样本点不是线性可分的,比如:
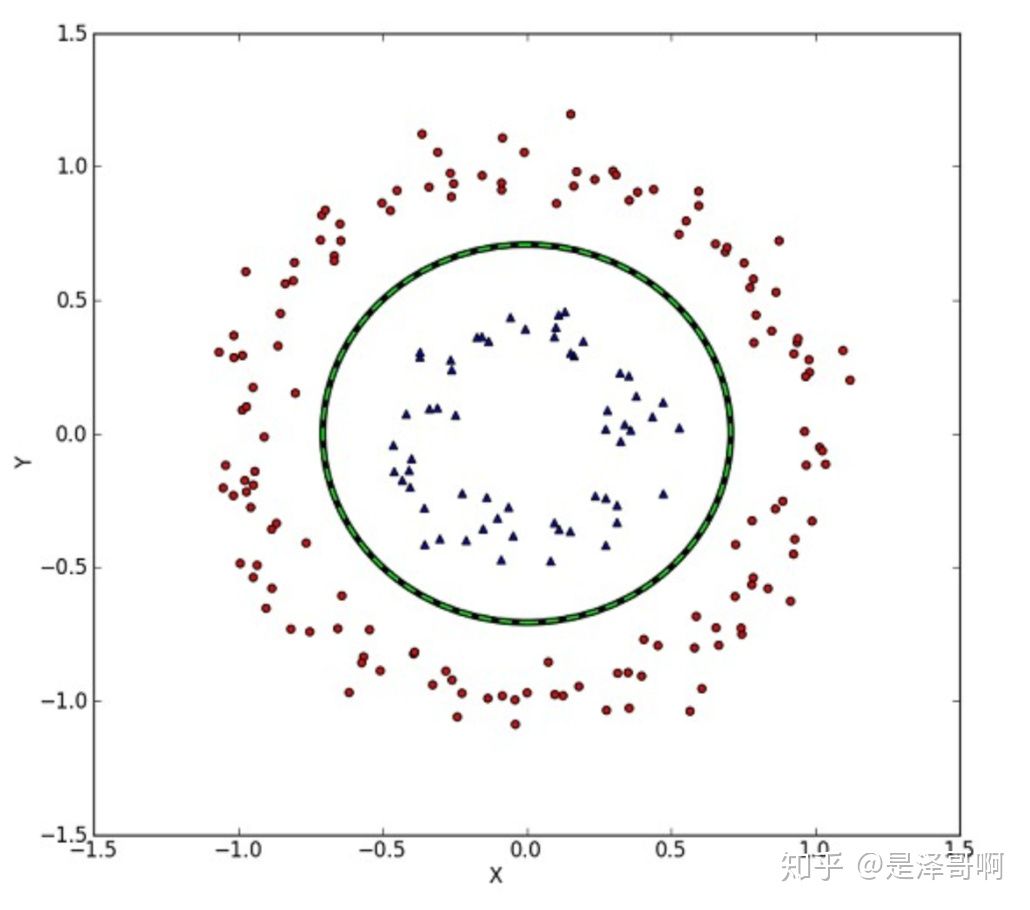
这种情况的解决方法就是:将二维线性不可分样本映射到高维空间中,让样本点在高维空间线性可分,比如:
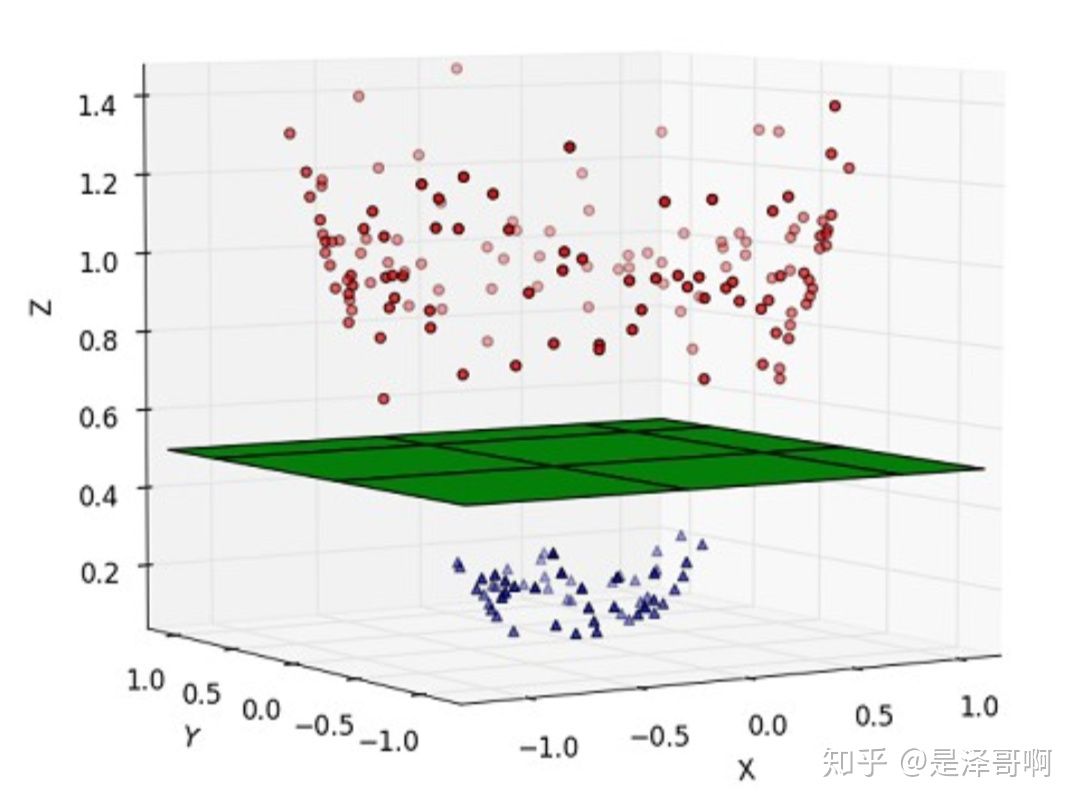
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里, 再通过间隔最大化的方 式,学习得到支持向量机,就是非线性 SVM。 我们用 \(\mathrm{x}\) 表示原来的样本点, 用 \(\phi(x)\) 表示 \(\mathrm{x}\) 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为: \(f(x)=w \phi(x)+b\) 。 对于非线性 SVM 的对偶问题就变成了: \[ \begin{aligned} & \min _\lambda\left[\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j\left(\phi\left(x_i\right) \cdot \phi\left(x_j\right)\right)-\sum_{j=1}^n \lambda_i\right] \\ & \text { s.t. } \quad \sum_{i=1}^n \lambda_i y_i=0, \quad \lambda_i \geq 0, \quad C-\lambda_i-\mu_i=0 \end{aligned} \] 可以看到与线性 SVM 唯一的不同就是:之前的 \(\left(x_i \cdot x_j\right)\) 变成了 \(\left(\phi\left(x_i\right) \cdot \phi\left(x_j\right)\right)\) 。
1.2 核函数的作用
我们不禁有个疑问:只是做个内积运算, 为什么要有核函数的呢?
这是因为 低维空间映射到高维空间后维度可能会很大, 如果将全部样本的点乘全部计算好, 这样的计算量太大了。
但如果我们有这样的一核函数 \(k(x, y)=(\phi(x), \phi(y)) , \quad x_i\) 与 \(x_j\) 在特征空间的内积等于它们在原始样本空间中通 过函数 \(k(x, y)\) 计算的结果, 我们就不需要计算高维甚至无穷维空间的内积了。 举个例子:假设我们有一个多项式核函数: \[ k(x, y)=(x \cdot y+1)^2 \] 带进样本点的后: \[ k(x, y)=\left(\sum_{i=1}^n\left(x_i \cdot y_i\right)+1\right)^2 \] 而它的展开项是: \[ \sum_{i=1}^n x_i^2 y_i^2+\sum_{i=2}^n \sum_{j=1}^{i-1}\left(\sqrt{2} x_i x_j\right)\left(\sqrt{2} y_i y_j\right)+\sum_{i=1} n\left(\sqrt{2} x_i\right)\left(\sqrt{2} y_i\right)+1 \] 如果没有核函数,我们则需要把向量映射成: \[ x^{\prime}=\left(x_1^2, \ldots, x_n^2, \ldots \sqrt{2} x_1, \ldots, \sqrt{2} x_n, 1\right) \] 然后在进行内积计算, 才能与多项式核函数达到相同的效果。可见核函数的引入一方面减少了我们计算量, 另一方面也减少了我们存储数据的内存使用量。
1.3 常见核函数
我们常用核函数有: 线性核函数【无映射】 \[ k\left(x_i, x_j\right)=x_i^T x_j \] - 优点: 有加速算法库、没有特征映射、过拟合风险低 - 缺点:只能处理线性
多项式核函数【映射,超参数】 \[ k\left(x_i, x_j\right)=\left(x_i^T x_j\right)^d \] 高斯核函数【映射,超参数】 \[ k\left(x_i, x_j\right)=\exp \left(-\frac{\left\|x_i-x_j\right\|}{2 \delta^2}\right) \]
- 表示能力强,但容易过拟合
- 高斯核没有多项核不稳定的问题
- 只有一个超参数
1.4 如何选择核函数?
其他核函数:拉普拉斯、sigmod、卡方、直方图交叉
可自定义和组合核函数
- 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。

1.5 核方法
核化LR [非线性] 正类: y = +1 负类 y= -1
\[ \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{x}_i+b\right)\right)\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2 \] 在本文由于通篇使用 \(\pm 1\) 表示正负类, 因此我们采用上述第二种记号方法。目前已经有对数几率回 归模型的实现, 比如 sklearn. linear_model.LogisticRegression。为了使得对数几率回归能解决非线性问题, 参考 SVM 的做法, 我们可以进行特征映射, 在特 征映射后的空间使用对数几率回归, 称为核化对数几率回归 (Kernel Logistic Regression), 其属 于正类的概率为: \[ \operatorname{Pr}(y=1 \mid \boldsymbol{x}):=\operatorname{sigm}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}(\boldsymbol{x})+b\right)=\frac{1}{1+\exp \left(-\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}(\boldsymbol{x})+b\right)\right)} \in[0,1] . \] 相应地优化目标改写为 \[ \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right)\right)\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2 \] 和原优化目标(公式 148)的区别在于 \(\boldsymbol{x} \in \mathbb{R}^d\) 变为了特征映射后的向量 \(\boldsymbol{\phi}(\boldsymbol{x}) \in \mathbb{R}^{\tilde{d}}\), 相应地核化对 数几率回归的参数 \(\boldsymbol{w} \in \mathbb{R}^{\tilde{d}}\) 的维度也提高至 \(\tilde{d}\) 。 注意到核化对数几率回归的目标函数满足表示定理, 因此参数的最优值 \(\boldsymbol{w}^{\star}\) 是特征映射后样本 的线性组合 \[ \boldsymbol{w}^{\star}=\sum_{i=1}^m \alpha_i \phi\left(\boldsymbol{x}_i\right) \] 其中线性组合系数 \(\left\{\alpha_i\right\}_{i=1}^m\) 待定, 将其代入公式 150 , \[ \begin{aligned} \min _{\boldsymbol{w}, b} & \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right)\right)\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2 \\ =\min _{\boldsymbol{\alpha}, b} & \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\left(\sum_{j=1}^m \alpha_j \boldsymbol{\phi}\left(\boldsymbol{x}_j\right)\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right)\right)\right) \\ & \left.+\frac{\lambda}{2}\left\|\sum_{i=1}^m \alpha_i \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)\right\|^2\right) \\ =\min _{\boldsymbol{\alpha}, b} & \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\sum_{j=1}^m \alpha_j \boldsymbol{\phi}\left(\boldsymbol{x}_j\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right)\right)\right) \\ & +\frac{\lambda}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_j\right) \\ = & \frac{1}{m} \sum_{\boldsymbol{\alpha}, b}^m \log \left(1+\exp \left(-y_i\left(\sum_{j=1}^m \alpha_j \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_j\right)+b\right)\right)\right) \\ & +\frac{\lambda}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_j\right) \\ & +\frac{1}{2} \sum_{i=1}^m \log \left(1+\exp \left(-y_i \sum_{j=1}^m \alpha_j \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)-y_i b\right)\right) \end{aligned} \] ##### 梯度下降求解:
核化LR的参数通常都非0,并且几乎用到所有训练的样本,预测效率比较低。