关联规则（3）FP-growth

发表于 分类于 ， ， 阅读次数： 本文字数： 3.5k 阅读时长 ≈ 6 分钟

一、FP-growth

前言——Apriori算法的缺陷

虽然Apriori算法能够有效计算频繁项集, 但是其缺点依旧存在：

  • 需要多次扫描数据集：Apriori算法中间有许多步骤都需要对某一个大集合（比如 \(D, L_k\) ） 进行遍历扫描，如果数据量庞大，那么遍历扫描仍然会占据大量的时间。
  • 可能会产生庞大的候选集：由于第 \(k\) 迭代的连接过程仍然需要进行 \(\left(\begin{array}{c}\left|L_k\right| /\ 2\end{array}\right)\) 次比较操作, 所以Apriori算法中途产生的候选集的数量依然巨大。

所以为什么一定要产生候选集？是否可以不通过产生候选集的方式来完成频繁模式挖掘呢？频繁模式增长(frequent pattern growth， 简称FP-growth)就是一种该方向的尝试。【原始事务数据转换为树状数据结构，减少扫描事务的成本】

1.1 算法流程

FP-growth主要采用一种分治的策略来解决该问题，我们可以用几个步骤来描述一下这种分治策略的大概步骤。

  1. 压缩数据集来表征每一个项，这个步骤一般是通过建立频繁模式树(frequent pattern tree，简称FP-tree)来实现的（其实就是字典树，很明显这是一种无损压缩方式）
  2. 统计每一个项在原数据集中出现的次数，并根据预先设定的support count去除低频项，然后根据出现次数对剩余项进行升序排序；从第一位项开始扫描频繁模式树的叶子节点，通过回溯得到每一个项对应的条件模式基(Condition Pattern Base，实则为叶子节点对应的路径集合)
  3. 根据条件模式基构建出条件频繁项集树(Conditional FP-tree，步骤和第一步完全一样，也就是根据条件模式基构建出一颗字典树)
  4. 根据条件FP-tree和support count得到最终的频繁项集

事务集如下：

TID itemset list
T100 I1, I2, I5
T200 I2, I4
T300 I2, I3
T400 I1, I2, I4
T500 I1, I3
T600 I2, I3
T700 I1, I3
T800 I1, I2, I3, I5
T900 I1, I2, I3
（1）建立模式频繁树

我们首先需要建立一颗模式频繁树，做法很简单，也就是直接建立一颗字典树。在建立之前，我们需要先对每一个项进行统计，并去除出现次数小于support count的项，然后排序。对于上表，这么做后的结果如下：

item count
I2 7
I1 6
I3 6
I4 2
I5 2

此处我们选择的support count为2，所以所有的项都被保留了下来。

然后我们需要对保留下来的项压缩成一个字典树，为了保证这颗字典树尽可能小，我们需要对事务集中的每一个项集进行排序，结果如下：

TID itemset list
T100 I2, I1, I5
T200 I2, I4
T300 I2, I3
T400 I2, I1, I4
T500 I1, I3
T600 I2, I3
T700 I1, I3
T800 I2, I1, I3, I5
T900 I2, I1, I3

字典树的根节点设为null，然后我们可以开始从第一条数据开始建立字典树，需要说明的是，这颗字典树的每个节点还需要维护一个count，这个count的含义是当前该节点被“经过”了多少次。下面的图中，每个结点被我标注为Ik : n的样子，代表当前节点名为Ik，count为n。

我们先加入T100：

然后加入T200：

img

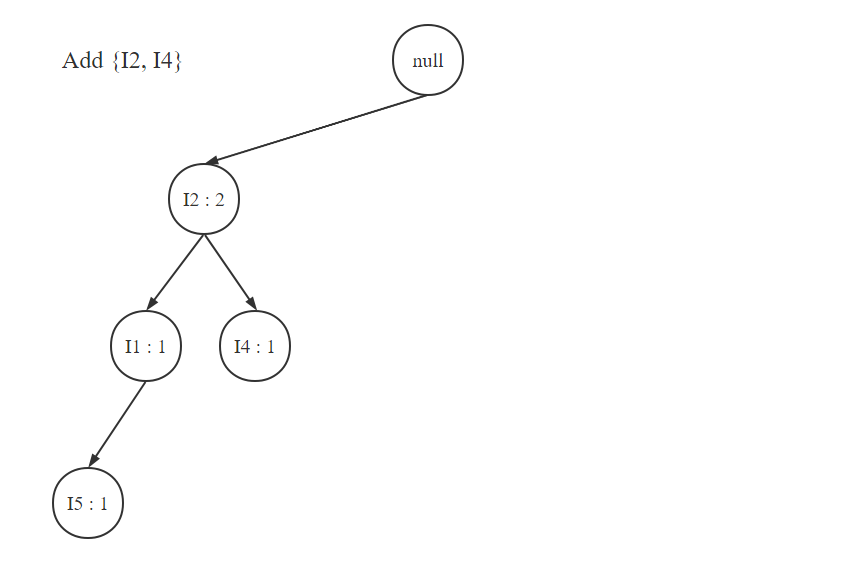
在频繁模式树建立完后，我们需要按照第一步中获取的表的顺序来遍历每一个项，由于我们之前获取的表中频数最小的项是I5，所以我们接下来先获取I5的条件模式基。

image-20230427164444928

item conditional pattern base
I5 {I2, I1 : 1}, {I2, I1, I3 : 1}
I4 {I2, I1 : 1}, {I2 : 1}
I3 {I2, I1 : 2}, {I2 : 2}, {I1 : 2}
I1 {I2 : 4}

由于I2不存在叶子节点上，所以I2不存在条件模式基

而fp-growth算法中的分治思想就体现在下面。可以看到，每个项对应的条件模式基本质就是一个项集，所以它们可以看成一个新的事务集。因此，原问题的总事务集就转换成了每个item对应的子事务集，而我们最终的频繁项集分别从每一个item对应的子事务集中产生，问题就被各个item分而治之了。

（3）从条件模式基中获取频繁项集

我们之前使用了字典树来压缩表征原事务集，那么对于我们的子事务集，我们也完全可以采用相同的步骤。不过需要注意，建立子事务集的频繁模式树之前，需要进行统计和基于support count的项的裁剪。比如对于I5的子事务集（也就是条件模式基），我们需要先统计，得到{I2 : 2, I1 : 2, I3 : 1}。由于我们的support count为2，所以我们需要去除count只为1的I3，然后排序得到I2, I1，剩下的事务集重构为{I2, I1 : 1}, {I2, I1 : 1}，很明显这两个前缀可以合并为{I2, I1 : 2}，然后我们画出这个裁剪后的子事务集的频繁模式树：

img

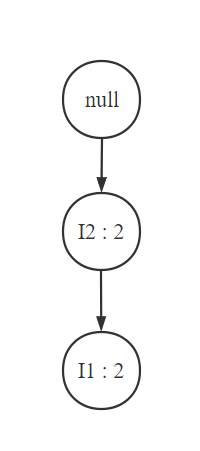
然后找出这棵频繁模式树的所有路径，可以看到上面的这棵频繁模式树只有一条路径，然后我们找出这条路径上节点所有可能的组合，也就是{I2, I1}, {I2}, {I1}，这也就是{I2, I1}的幂集。然后对于每一个组合类型，我们再加上I5，于是就得到了这条路径上得到的频繁项集：{I2, I1, I5}, {I2, I5}, {I1, I5}。所有路径上的频繁项集合并起来就是I5对应的频繁项集。

我们再举一个例子，就举I3吧。首先统计项得到 {I2 : 4, I1 : 4}都大于2，不需要裁剪，排序后得到的子事务集不变，还是{I2, I1 : 2}, {I2 : 2}, {I1 : 2}，构建该子数据集的频繁模式树：

img

然后找出FP-tree的所有路径：{I2, I1}和{I1}。对于路径{I2, I1}在，找出所有的组合{I2, I1}, {I2}和{I1}，加上I3得到{I2, I1, I3}, {I2, I3}, {I1, I3}；对于路径{I1}，找出所有的组合{I1}，加上I3得到{I1, I3}。

遍历完所有路径后，将得到的频繁项集集合取并集，得到{I2, I1, I3}, {I2, I3}, {I1, I3}。所以I3对应的频繁项集就是{I2, I1, I3}, {I2, I3}, {I1, I3}。

（4）整合每个项的频繁项集，就是答案啦

其余的两个项也是同样的操作过程，最终的每个项对应的频繁项集如下表所示：

item frequent itemsets
I5 {I2, I1, I5}, {I2, I5}, {I1, I5}
I4 {I2, I4}
I3 {I2, I3}, {I1, I3}, {I2, I1}
I1 {I2, I1}

至此FP-growth算法执行结束。可以看到，由于采用了分治的方法，所以FP-growth得到的结果是根据项进行分层的，也就是说结果对于特定的某一个项有很强的指向作用。比如我们只想要研究哪些值和I5最频繁出现，我们可以只看I5产生的频繁项集。

1.2 Pyspark demo实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import pandas as pd
from pyspark.sql import SparkSession
from pyspark.ml.fpm import FPGrowth
from pyspark.sql.functions import *
from collections import defaultdict

spark = SparkSession.builder.appName("reduceByKey").getOrCreate()
# 创建DataFrame
data = spark.createDataFrame([
    (1, [1, 2, 5]),
    (2, [1, 2, 3, 5]),
    (3, [1, 2])
], ["id", "items"])

# 初始化FPGrowth模型
fp = FPGrowth(itemsCol="items", minSupport=0.5, minConfidence=0.6)
# 训练FPGrowth模型
model = fp.fit(data)
# 展示频繁项集
model.freqItemsets.show()

参考文献

  • 数据挖掘随笔（二）FP-growth算法——一种用于频繁模式挖掘的模式增长方式(Python实现)：https://zhuanlan.zhihu.com/p/411594391
  • pyspark.ml.fpm.``FPGrowth:https://spark.apache.org/docs/latest/api/python/reference/api/pyspark.ml.fpm.FPGrowth.html