度量学习(1)KNN
一、什么是KNN【KD树 + SIFT+BBF算法】
1.1 KNN的通俗解释
何谓K近邻算法,即K-Nearest Neighbor algorithm,简称KNN算法,单从名字来猜想,可以简单粗暴的认为是:K个最近的邻居,当K=1时,算法便成了最近邻算法,即寻找最近的那个邻居。
用官方的话来说,所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例(也就是上面所说的K个邻居),这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
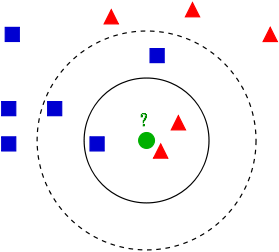
如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说,现在,我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形or红色小三角形),KNN就是解决这个问题的。
如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
于此我们看到,当无法判定当前待分类点是从属于已知分类中的哪一类时,我们可以依据统计学的理论看它所处的位置特征,衡量它周围邻居的权重,而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想。
1.2 近邻的距离度量
我们看到,K近邻算法的核心在于找到实例点的邻居,这个时候,问题就接踵而至了,如何找到邻居,邻居的判定标准是什么,用什么来度量。这一系列问题便是下面要讲的距离度量表示法。
有哪些距离度量的表示法(普及知识点,可以跳过):
1.2.1 欧式距离
欧氏距离, 最常见的两点之间或多点之间的距离表示法, 又称之为欧几里得度量, 它定义于欧几里得空间中, 如点 \(x=(x 1, \ldots, x n)\) 和 \(y=(y 1, \ldots, y n)\) 之间的距离为: \[ d(x, y)=\sqrt{\left(x_1-y_1\right)^2+\left(x_2-y_2\right)^2+\ldots+\left(x_n-y_n\right)^2}=\sqrt{\sum_{i=1}^n\left(x_i-y_i\right)^2} \] 二维平面上两点 \(a(x 1, y 1)\) 与 \(b(x 2, y 2)\) 间的欧氏距离: \[ d_{12}=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \] 三维空间两点 \(a(x 1, y 1, z 1)\) 与 \(b(x 2, y 2, z 2)\) 间的欧氏距离: \[ d_{12}=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2+\left(z_1-z_2\right)^2} \] 两个n维向量 \(a(x 11, \times 12, \ldots, x 1 n)\) 与 \(b(\times 21, \times 22, \ldots, \times 2 n)\) 间的欧氏距离: \[ d_{12}=\sqrt{\sum_{k=1}^n\left(x_{1 k}-x_{2 k}\right)^2} \] 也可以用表示成向量运算的形式:
1.2.2 曼哈顿距离
曼哈顿距离, 我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离, 也就是在欧几里得空间的固定 直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上, 坐标 \((x 1, y 1)\) 的点P1与坐标 \((\mathrm{x} 2, \mathrm{y} 2)\) 的点P2的曼哈顿距离为: \(\left|x_1-x_2\right|+\left|y_1-y_2\right|\), 要注意的是, 曼哈顿距离依赖座标系统的转度, 而非系统在座标轴上的平移或映射。
通俗来讲, 想象你在曼哈顿要从一个十字路口开车到另外一个十字路口, 驾驶距离是两点间的直线距离吗? 显 然不是, 除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”, 此即曼哈顿距离名称的来源, 同时, 曼 哈顿距离也称为城市街区距离(City Block distance)。
二维平面两点 \(a(x 1, y 1)\) 与 \(b(x 2, y 2)\) 间的曼哈顿距离 \[ d_{12}=\left|x_1-x_2\right|+\left|y_1-y_2\right| \] 两个 \(n\) 维向量 \(a(x 11, x 12, \ldots, x 1 n)\) 与 \(b(x 21, x 22, \ldots, x 2 n)\) 间的曼哈顿距离 \[ d_{12}=\sum_{k=1}^n\left|x_{1 k}-x_{2 k}\right| \]
1.2.3 切比雪夫距离
切比雪夫距离, 若二个向量或二个点 \(\mathrm{p} 、\) and \(\mathrm{q}\), 其座标分别为 \(\mathrm{P}\) 及 \(\mathrm{qi}\), 则两者之间的切比雪夫距离定义如 下: \(D_{C h e b y s h e v}(p, q)=\max _i\left(\left|p_i-q_i\right|\right)\)
这也等于以下Lp度量的极值: \(\lim _{x \rightarrow \infty}\left(\sum_{i=1}^n\left|p_i-q_i\right|^k\right)^{1 / k}\), 因此切比雪夫距离也称为 \(\infty\) 度量。
以数学的观点来看, 切比雪夫距离是由一致范数 (uniform norm) (或称为上确界范数)所衍生的度量, 也 是超凸度量(injective metric space)的一种。
在平面几何中, 若二点 \(\mathrm{p} \mathrm{q}\) 的直角坐标系坐标为 \((x 1, y 1)\) 及 \((x 2, y 2)\), 则切比雪夫距离为: \(D_{C h e s s}=\max \left(\left|x_2-x_1\right|,\left|y_2-y_1\right|\right)\)
玩过国际象棋的朋友或许知道,国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1) 走到格子(x2,y2)最少需要多少步? 。你会发现最少步数总是 \(\max (|x 2-x 1| ,|y 2-y 1|)\) 步 。有一种类似的 一种距离度量方法叫切比雪夫距离。
二维平面两点 \(a(x 1, y 1)\) 与 \(b(x 2, y 2)\) 间的切比雪夫距离 : \[ d_{12}=\max \left(\left|x_2-x_1\right|,\left|y_2-y_1\right|\right) \] 两个 \(n\) 维向量 \(a(x 11, x 12, \ldots, x 1 n)\) 与 \(b(x 21, x 22, \ldots, x 2 n)\) 间的切比雪夫距离 : \[ d_{12}=\max _i\left(\left|x_{1 i}-x_{2 i}\right|\right) \]
简单说来,各种“距离”的应用场景简单概括为:
- 空间:欧氏距离,
- 路径:曼哈顿距离,国际象棋国王:切比雪夫距离,
- 以上三种的统一形式:闵可夫斯基距离,
- 加权:标准化欧氏距离,
- 排除量纲和依存:马氏距离,
- 向量差距:夹角余弦,
- 编码差别:汉明距离,
- 集合近似度:杰卡德类似系数与距离,
- 相关:相关系数与相关距离。
1.3 K值选择
- 如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
- 如果选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
- K=N,则完全不足取,因为此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的累,模型过于简单,忽略了训练实例中大量有用信息。
在实际应用中,K值一般取一个比较小的数值,例如采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的K值。
1.4 KNN最近邻分类算法的过程
- 计算测试样本和训练样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
- 对上面所有的距离值进行排序;
- 选前 k 个最小距离的样本;
- 根据这 k 个样本的标签进行投票,得到最后的分类类别;
关于KNN的一些问题
在k-means或kNN,我们是用欧氏距离来计算最近的邻居之间的距离。为什么不用曼哈顿距离?
答:我们不用曼哈顿距离,因为它只计算水平或垂直距离,有维度的限制。另一方面,欧式距离可用于任何空间的距离计算问题。因为,数据点可以存在于任何空间,欧氏距离是更可行的选择。例如:想象一下国际象棋棋盘,象或车所做的移动是由曼哈顿距离计算的,因为它们是在各自的水平和垂直方向的运动。
KD-Tree相比KNN来进行快速图像特征比对的好处在哪里?
答:极大的节约了时间成本.点线距离如果 > 最小点,无需回溯上一层,如果<,则再上一层寻找。