理论基础（4）回归评价指标

发表于 2022-03-24 更新于 2023-04-26 分类于算法，机器学习，理论基础阅读次数：本文字数： 5.4k 阅读时长 ≈ 10 分钟

一、回归问题评价指标

均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss、分位数损失 Quantile Loss

机器学习中的监督学习本质上是给定一系列训练样本 \(\left(x_i, y_i\right)\), 尝试学习 \(x \rightarrow y\) 的映射关系, 使得给定一个 \(x\), 即便这个 \(x\) 不在训练样本中, 也能够得到尽量接近真实 \(y\) 的输出 \(\hat{y}\) 。而损失函数 (Loss Function) 则是这个过程中关键的一个组成部分, 用来衡量模型的输出 \(\hat{y}\) 与真实的 \(y\) 之间的差距, 给模型的优化指明方向。

1.1 均方差损失 MSE、L2 loss

1.1.1 基本形式与原理

均方差Mean Squared Error (MSE)损失是机器学习、深度学习回归任务中最常用的一种损失函数, 也称为 L2 Loss。其基本形式如下: \[ J_{M S E}=\frac{1}{N} \sum_{i=1}^N\left(y_i-\hat{y_i}\right)^2 \] 从直觉上理解均方差损失，这个损失函数的最小值为 0 （当预测等于真实值时），最大值为无穷大。下图是对于真实值 \(y=0\), 不同的预测值 \([-1.5,1.5]\) 的均方差损失的变化图。横轴是不同的预测值, 纵轴是均方差损失, 可以看到随着预测与真实值绝对误差 \(|y-\hat{y}|\) 的增加, 均方差损失呈二次方地增加。

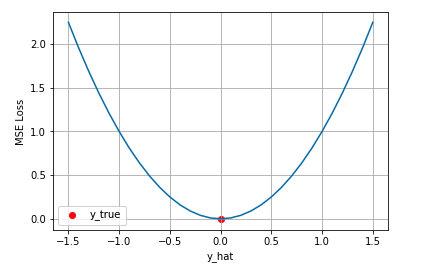
1.1.2 背后的假设

【独立同分布-中心极限定理】：如果 \(\left\{X_n\right\}\) 独立同分布, 且 \(\mathbb{E} X=\mu, \mathbb{D} X=\sigma^2>0\) ，则 \(\mathrm{n}\) 足够大时 \(\bar{X}_n\) 近似服从正态分布 \(N\left(\mu, \frac{\sigma^2}{n}\right)\) 即 \[ \lim _{n \rightarrow \infty} P\left(\frac{\bar{X}_n-\mu}{\sigma / \sqrt{n}}<a\right)=\Phi(a)=\int_{-\infty}^a \frac{1}{\sqrt{2 \pi}} e^{-t^2 / 2} d t \] 实际上在一定的假设下, 我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布 \((\mu=0, \sigma=1)\) ，则给定一个 \(x_i\) 模型输出真实值 \(y_i\) 的概率为 \[ p\left(y_i \mid x_i\right)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\left(y_i-\hat{y}_i\right)^2}{2}\right) \] 进一步我们假设数据集中 \(\mathrm{N}\) 个样本点之间相互独立, 则给定所有 \(x\) 输出所有真实值 \(y\) 的概率, 即似然 Likelihood, 为所有 \(p\left(y_i \mid x_i\right)\) 的累乘 \[ L(x, y)=\prod_{i=1}^N \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{\left(y_i-\hat{y}_i\right)^2}{2}\right) \] 通常为了计算方便，我们通常最大化对数似然Log-Likelihood \[ L L(x, y)=\log (L(x, y))=-\frac{N}{2} \log 2 \pi-\frac{1}{2} \sum_{i=1}^N\left(y_i-\hat{y_i}\right)^2 \] 去掉与 \(\hat{y_i}\) 无关的第一项, 然后转化为最小化负对数似然 Negative Log-Likelihood \[ N L L(x, y)=\frac{1}{2} \sum_{i=1}^N\left(y_i-\hat{y}_i\right)^2 \] 可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下, 最小化均方差损失函数与极大似然估计本质上是一致的, 因此在这个假设能被满足的场景中（比如回归）, 均方差损失是一个很好的损失函数选择；当这个假设没能被满足的场景中（比如分类），均方差损失不是一个好的选择。

hulu 百面机器学习 —— 平方根误差的”意外“

95%的时间区间效果很好，RMSE指标居高不下的原因？ \[ J_{M S E}=\frac{1}{N} \sum_{i=1}^N\left(y_i-\hat{y_i}\right)^2 \] 一般情况下RSME能反应预测值与真实值的偏离程度，但是易受离群点的影响；

解决方案：

数据预处理将噪音去掉
将离群点的产生机制建模进去
更鲁棒的模型评估指标：平均绝对百分比误差（MAPE），分位数损失

1.2 平均绝对误差 MAE

1.2.1 基本形式与原理

平均绝对误差 Mean Absolute Error (MAE) 是另一类常用的损失函数, 也称为 L1 Loss。其基本形式如下 \[ J_{M A E}=\frac{1}{N} \sum_{i=1}^N\left|y_i-\hat{y_i}\right| \] 同样的我们可以对这个损失函数进行可视化如下图, MAE 损失的最小值为 0 (当预测等于真实值时），最大值为无穷大。可以看到随着预测与真实值绝对误差 \(|y-\hat{y}|\) 的增加, MAE 损失呈线性增长。

1.2.2 背后的假设

同样的我们可以在一定的假设下通过最大化似然得到 MAE 损失的形式, 假设模型预测与真实值之间的误差服从拉普拉斯分布 Laplace distribution \((\mu=0, b=1)\), 则给定一个 \(x_i\) 模型输出真实值 \(y_i\) 的概率为 \[ p\left(y_i \mid x_i\right)=\frac{1}{2} \exp \left(-\left|y_i-\hat{y_i}\right|\right) \] 与上面推导 MSE 时类似, 我们可以得到的负对数似然实际上就是 MAE 损失的形式 \[ \begin{gathered} L(x, y)=\prod_{i=1}^N \frac{1}{2} \exp \left(-\left|y_i-\hat{y}_i\right|\right) \\ L L(x, y)=N \ln \frac{1}{2}-\sum_{i=1}^N\left|y_i-\hat{y}_i\right| \\ N L L(x, y)=\sum_{i=1}^N\left|y_i-\hat{y}_i\right| \end{gathered} \]

1.3 MAE 与 MSE 区别

MAE 和 MSE 作为损失函数的主要区别是：MSE 损失相比 MAE 通常可以更快地收敛，但 MAE 损失对于 outlier 更加健壮，即更加不易受到 outlier 影响。

MSE 通常比 MAE 可以更快地收敛。当使用梯度下降算法时, MSE 损失的梯度为 \(-\hat{y}_i\), 而 MAE 损失的梯度为 \(\pm 1\) , 即 MSE 的梯度的 scale 会随误差大小变化, 而 MAE 的梯度的 scale 则一直保持为 1 , 即便在绝对误差 \(\left|y_i-\hat{y}_i\right|\) 很小的时候 MAE 的梯度 scale 也同样为 1 , 这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题, 但是总的来说, 损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。
MAE 对于异常值（outlier）更加 robust。我们可以从两个角度来理解这一点：
- 第一个角度是直观地理解，下图是 MAE 和 MSE 损失画到同一张图里面，由于MAE 损失与绝对误差之间是线性关系，MSE 损失与误差是平方关系，当误差非常大的时候，MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时，MSE 会产生一个非常大的损失，对模型的训练会产生较大的影响。
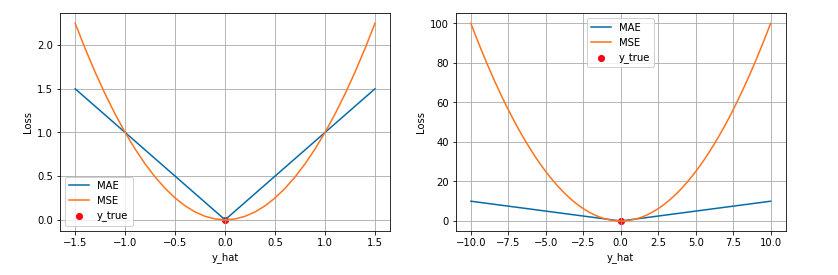
- 第二个角度是从两个损失函数的假设出发，MSE 假设了误差服从高斯分布，MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust。参考下图（来源：Machine Learning: A Probabilistic Perspective 2.4.3 The Laplace distribution Figure 2.8），当右图右侧出现了 outliers 时，拉普拉斯分布相比高斯分布受到的影响要小很多。因此以拉普拉斯分布为假设的 MAE 对 outlier 比高斯分布为假设的 MSE 更加 robust。

1.4 Huber Loss

在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定

在误差较大时使用 MAE 可以降低 outlier 的影响，使训练对 outlier 更加健壮。

上文我们分别介绍了 MSE 和 MAE 损失以及各自的优缺点, MSE 损失收玫快但容易受 outlier 影响, MAE 对 outlier 更加健壮但是收玫慢, Huber LosS 则是一种将 MSE 与 MAE 结合起来, 取两者优点的损失函数, 也被称作 Smooth Mean Absolute Error Loss 。其原理很简单, 就是在误差接近 0 时使用 MSE, 误差较大时使用 MAE, 公式为 \[ J_{\text {huber }}=\frac{1}{N} \sum_{i=1}^N \mathbb{I}_{\left|y_i-\hat{y_i}\right| \leq \delta} \frac{\left(y_i-\hat{y_i}\right)^2}{2}+\mathbb{I}_{\left|y_i-\hat{y}_i\right|>\delta}\left(\delta\left|y_i-\hat{y_i}\right|-\frac{1}{2} \delta^2\right) \] 上式中 \(\delta\) 是 Huber Loss 的一个超参数, \(\delta\) 的值是 MSE 和 MAE 两个损失连接的位置。上式等号右边第一项是 MSE 的部分, 第二项是 MAE 部分, 在 MAE 的部分公式为 \(\delta\left|y_i-\hat{y_i}\right|-\frac{1}{2} \delta^2\) 是为了保证误差 \(|y-\hat{y}|= \pm \delta\) 时 MAE 和 MSE 的取值一致，进而保证 Huber Loss 损失连续可导。

下图是 \(\delta=1.0\) 时的 Huber Loss, 可以看到在 \([-\delta, \delta]\) 的区间内实际上就是 MSE 损失, 在 \((-\infty, \delta)\) 和 \((\delta, \infty)\) 区间内为 MAE损失。

1.5 分位数损失 Quantile Loss

MAE 中分别用不同的系数控制高估和低估的损失，进而实现分位数回归

分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法，通常的回归算法是拟合目标值的期望或者中位数，而分位数回归可以通过给定不同的分位点，拟合目标值的不同分位数。

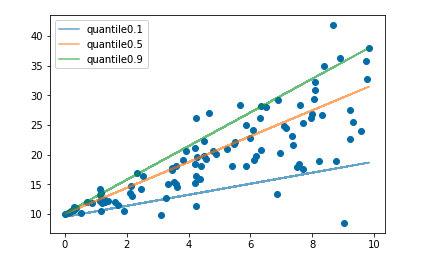
分位数回归是通过使用分位数损失 Quantile Loss 来实现这一点的, 分位数损失形式如下, 式中的 r 分位数系数。 \[ J_{\text {quant }}=\frac{1}{N} \sum_{i=1}^N \mathbb{I}_{\hat{y}_i \geq y_i}(1-r)\left|y_i-\hat{y_i}\right|+\mathbb{I}_{\hat{y}_i<y_i} r\left|y_i-\hat{y_i}\right| \] 我们如何理解这个损失函数呢? 这个损失函数是一个分段的函数, 将 \(\hat{y}_i \geq y_i \quad\) (高估) 和 \(\hat{y}_i<y_i \quad\) (低估) 两种情况分开来, 并分别给予不同的系数。当 \(r>0.5\) 时, 低估的损失要比高估的损失更大, 反过来当 \(r<0.5\) 时, 高估的损失比低估的损失大; 分位数损失实现了分别用不同的系数控制高估和低估的损失, 进而实现分位数回归。特别地, 当 \(r=0.5\) 时, 分位数损失退化为 MAE 损失, 从这里可以看出 MAE 损失实际上是分位数损失的一个特例一中位数回归。

下图是取不同的分位点 \(0.2 、 0.5 、 0.6\) 得到的三个不同的分位损失函数的可视化，可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的, 而 0.5 实际上就是 MAE。

1.6 平均绝对百分误差 MAPE

虽然平均绝对误差能够获得一个评价值, 但是你并不知道这个值代表模型拟合是优还是劣, 只有通过对比才能达到效果。当需要以相对的观点来衡量误差时, 则使用MAPE。平均绝对百分误差（Mean Absolute Percentage Error, MAPE）是对 MAE 的一种改进, 考虑了绝对误差相对真实值的比例。 - 优点：考虑了预测值与真实值的误差。考虑了误差与真实值之间的比例。 \[ M A P E=\frac{100}{m} \sum_{i=1}^m\left|\frac{y_i-f\left(x_i\right)}{y_i}\right| \] 在某些场景下, 如房价从 \(5 K\) 到 \(50 K\) 之间, \(5 K\) 预测成 \(10 K\) 与 \(50 K\) 预测成 \(45 K\) 的差别是非常大的, 而平均绝对百分误差考虑到了这点。