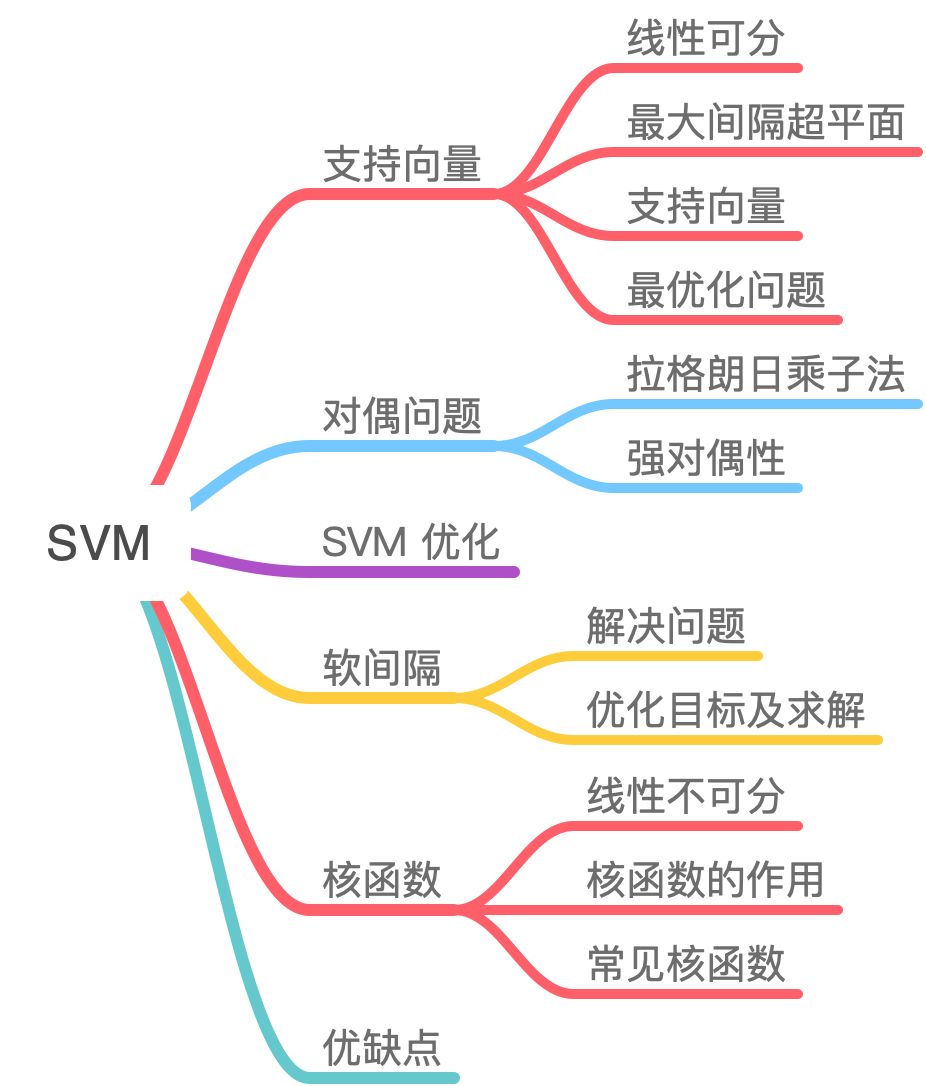
支持向量机(4)支持向量回归 & 多分类
SVM 是一个非常优雅的算法,具有完善的数学理论,虽然如今工业界用到的不多,但还是决定花点时间去写篇文章整理一下。
本质:SVM 想要的就是找到各类样本点到超平面的距离最远,也就是找到最大间隔超平面。为了对数据中的噪声有一定的容忍能力。以几何的角度,在丰富的数据理论的基础上,简化了通常的分类和回归问题。
几何意义:找到一个超平面将特征空间的正负样本分开,最大分隔(对噪音有一定的容忍能力);
间隔表示:划分超平面到属于不同标记的最近样本的距离之和;
一、支持向量回归 SVR
https://blog.csdn.net/ch18328071580/article/details/94168411
支持向量在隔代之外
1.1 SVR与一般线性回归的区别
| SVR | 线性回归 |
|---|---|
| 数据在间隔带内则不计算损失,当且仅当f(x)与y之间的差距的绝对值大于ϵ才计算损失 | 只要f(x)与y不相等时,就计算损失 |
| 通过最大化间隔带的宽度与最小化总损失来优化模型 | 通过梯度下降之后求均值来优化模型 |
岭回归: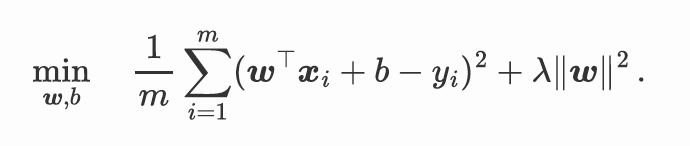
支持向量回归:我们假设f(x)与y之间最多有一定的偏差,大于偏差才计数损失
\[ \min _{w, b} \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} l_{\epsilon}\left(f\left(x_{i}\right), y_{i}\right) \] 其中C为正则化常数, \(l_{\epsilon}\) 是图中所示的 \(\epsilon\)-不敏感损失 ( \(\epsilon\)-insensitive loss)函数: \[ l_{\epsilon}(\mathrm{z})= \begin{cases}0, & \text { if }|z| \leq \epsilon \\ |z|-\epsilon, & \text { otherwise }\end{cases} \] 引入松弛变量 \(\xi_{i}\) 和 \(\left(\xi_{i}\right)\), 可将式重写为: \[ \begin{array}{ll} \min _{w, b, \xi_{i}, \xi_{i}} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m}\left(\xi_{i}, \widehat{\xi}_{i}\right) \\ \text { s.t. } & f\left(x_{i}\right)-y_{i} \leq \epsilon+\xi_{i} \\ & y_{i}-f\left(x_{i}\right) \leq \epsilon+\widehat{\xi}_{i} \\ & \xi_{i} \geq 0, \hat{\xi}_{i} \geq 0, i=1,2, \ldots m \end{array} \] 引入拉格朗日乘子 \(\mu_{i}\),
\(L(w, b, \alpha, \hat{\alpha}, \xi, \hat{\xi}, \mu, \hat{\mu})\) \(=\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m}\left(\xi_{i}+\widehat{\xi}_{i}\right)-\sum_{i=1}^{m} \xi_{i} \mu_{i}-\sum_{i=1}^{m} \widehat{\xi}_{i} \widehat{\mu_{i}}\) \(+\sum_{i=1}^{m} \alpha_{i}\left(f\left(x_{i}\right)-y_{i}-\epsilon-\xi_{i}\right)+\sum_{i=1}^{m} \widehat{\alpha_{i}}\left(y_{i}-f\left(x_{i}\right)-\epsilon-\widehat{\xi}_{i}\right)\)
再令 \(L(w, b, a, \hat{a}, \xi, \hat{\xi}, \mu, \mu)\) 对 \(w, b, \xi_{i}, \hat{\xi}_{i}\) 的偏导为零可得: \[ w=\sum_{i=1}^{m}\left(\widehat{\alpha_{i}}-\alpha_{i}\right) x_{i} \] 上述过程中需满足KKT条件, 即要求: \[ \left\{\begin{array}{c} \alpha_{i}\left(f\left(x_{i}\right)-y_{i}-\epsilon-\xi_{i}\right)=0 \\ \widehat{\alpha_{i}}\left(y_{i}-f\left(x_{i}\right)-\epsilon-\widehat{\xi}_{i}\right)=0 \\ \alpha_{i} \widehat{\alpha_{i}}=0, \xi_{i} \widehat{\xi}_{i}=0 \\ \left(C-\alpha_{i}\right) \xi_{i}=0,\left(C-\widehat{\alpha_{i}}\right) \widehat{\xi}_{i}=0 . \end{array}\right. \]
二、多分类 SVM
2.1 多分类问题
- 多分类问题拆解成若干个二分类问题,对于每个二分类训练一个分类器。
- one vs one 拆解:K(K-1)/2 个分类器。
- one vs Rest 拆解:K个分类器

2.2 多分类线性SVM
层次支持向量机
回顾二分类
\[ \begin{aligned} & \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \max \left(1-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{x}_i+b, 0\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2\right. \\ = & \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \max \left(1-y_i s\left(\boldsymbol{x}_i\right), 0\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2 . \end{aligned} \]
- 多分类线性SVM
\[ \min _{\boldsymbol{W}, \boldsymbol{b}} \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \mathbb{I}\left(k \neq y_i\right) \cdot \max \left(1-s\left(\boldsymbol{x}_i\right)_{y_i}+s\left(\boldsymbol{x}_i\right)_k, 0\right)+\frac{\lambda}{2} \sum_{k=1}^K\left\|\boldsymbol{w}_k\right\|^2, \]