关联规则(2)Apriori
一、Apriori算法
Apriori算法是常用的用于挖掘出数据关联规则的算法,它用来找出数据值中频繁出现的数据集合,找出这些集合的模式有助于我们做一些决策。
支持度:关联规则A->B的支持度support=P(AB),指的是事件A和事件B同时发生的概率;
置信度:指的是发生事件A的基础上发生事件B的概率;
频繁k项集:频繁项集表示的就是在数据集中频繁出现的项集(可以是一个,也可以是多个)。如果事件A中包含k个元素,那么称这个事件A为k项集,并且事件A满足最小支持度阈值的事件称为频繁k项集;
1.1 背景
对于Apriori算法,我们使用支持度来作为我们判断频繁项集的标准。Apriori算法的目标是找到最大的K项频繁集。
记 \(\mathcal{I}=\left\{I_1, I_2, \ldots, I_m\right\}\) 为一个项集, 其中的 \(I_k(k=0,1, \ldots, m)\) 代表所有可能出现的子项。
举例:
比如你作为一家大型连锁超市的数据分析师,你发现前台给你发的大量顾客的购物清单数据中,鸡蛋+面包+牛奶这样的组合是清单中的常客,且符合一些不可言喻的约束条件,那么鸡蛋、面包和牛奶这三样商品经常一起出现这样一个规律就算是购物清单数据中的频繁模式。其中,鸡蛋,面包,牛奶这样一个集合我们就称为一个频繁项集(frequent itemset)。
| TID | transaction |
|---|---|
| T1 | 鸡蛋,牙膏,牛排,牛奶,面包 |
| T2 | 鸡蛋,亚麻籽,橄榄油,牛奶,面包 |
| T3 | 鸡蛋,泡芙,奶油,牛奶,面包 |
| T4 | 鸡蛋,低筋面粉,糖粉,黄油,牛奶 |
TID是每一个顾客的账单的编号,上述表格中我们有4个顾客的交易记录。
- 给定事务集 \(D\), 找出一组关联规则(association rule) \(A \subseteq \mathcal{I} \wedge B \subseteq \mathcal{I} \wedge A \Rightarrow B\) 。它的意思 是 \(A\) 和 \(B\) 相关联, 由 \(A\) 可以推出 \(B\) 。比如 \(A=\{\) 鸡蛋, 牛奶 \(\}, B=\{\) 面包 \(\}\), 那么 \(A \Rightarrow B\) 可以认为是买了鸡蛋和牛奶的顾客有大概率也会去买面包。这个过程我们称为关联规则挖掘(association rule mining)
- 给定事务集 \(D\), 找出蕴含其中的频繁项集。比如通过example1中的表格, 我们挖掘出了用户喜欢鸡蛋+面包+牛奶这样的模式。这个过程我们称为频繁模式挖掘(frequent pattern mining)
1.2 关联规则挖掘
为了后续的度量, 需要引入两个相当相当简单的概念, support和confidence。记 \(A\) 和 \(B\) 是 \(\mathcal{I}\) 中的两个子集, 那么则 \(A\) 和 \(B\) 在 \(D\) 中同时发生的概率称为support: \[ \operatorname{support}(A \Rightarrow B)=P(A \cup B) \] \(A\) 发生的前提下, \(B\) 在 \(D\) 发生的概率称为confidence: \[ \text { confidence }(A \Rightarrow B)=\frac{P(A \cup B)}{P(A)}=\frac{\operatorname{support}(A \cup B)}{\operatorname{support}(A)} \] 事实上, 书上对support的定义有点模糊, 我的理解是support就是一个很简单的频度度量, 所以 \(\operatorname{support}(A)\) 就代表 \(A\) 在 \(D\) 出现的频率。
还有一点,定义在 \(D\) 上的频度的计算公式如下: \[ P(A)=\frac{1}{|D|} \sum_{i=1}^{|D|} \mathbb{I}\left(A \subseteq T_i\right) \] 其中 \(\mathbb{I}(c)\) 为指示函数, \(c\) 为真,则返回 \(1 ; c\) 为假,则返回0。
很明显, 对于计算出的值, 我们需要设置人为的阈值才能判定 \(A\) 和 \(B\) 是否为一个关联规则。假定我们设置了两个阈值 \(s\) 和 \(c\) 。那么如果 \(\operatorname{support}(A \Rightarrow B) \geq s \wedge \operatorname{confidence}(A \Rightarrow B) \geq c\) , 我们就说 \(A \Rightarrow B\) 是一条关联规则。它的实际意义可是买了{鸡蛋,牛奶} 很有可能还会去买 {面包}。
这就是关联规则挖掘的最简单的做法, 由此, 我们可以用两步来总结关联规则挖掘的步骤:
- 找出所有可能的频繁项集。频繁项集的定义为support在事务集中出现频率大于设定阈值min_sup的项集。
- 在找出的频繁项集中生成强关联规则。符合强相关联规则的频繁项集对需要满足其support和 confidence都分别大于预先设定好的阈值。
Ha , 所以我们需要先找出事务集中所有可能的频繁项集。我们发现, 在support度量意义下的频繁项集的定义很简单, 只需要出现频率大于设定阈值的项集就算是频繁项集。但是我们找频繁项集的搜索空间是什么, 是总项集\(\mathcal{I}\) 的幂集耶, 这玩意儿的大小为\(2^{|\mathcal{I}|-1}=2^{m-1}\) 。
那么我们的dummy算法时间复杂度直接升天, 光是最外层的搜索就已经是指数 级的复杂度了, 显然这不是一个有效的算法。
而当我们找到有限个频繁项集后, 只需要通过计算所有的频繁项集中两两是否满足confidence和 support分别大于预先设定的值就行了, 这一步的时间复杂度不会很大。所以重点还是在于如何设计出找到频繁项集的有效算法。
所以于此, 我们需要引入一些有意思的频繁项集的搜索算法。其中最简单的就是1994年提出的 Apriori算法了。
1.3 Apriori算法
由于频繁项集的搜索空间是指数级别的,所以我们需要想办法来缩减搜索空间大小。Apriori提供了一种以连接剪枝为一个迭代循环的算法来有效减小了搜索空间。之所以取名为Apriori,因为算法使用了项集本身的一些先验信息(prio [ˈpraɪə(r)] ),加上作者之一是Agrawal,故取名为Apriori。
Apriori到底在干什么,一般而言,我们在搜索空间找东西可以分成两种——自上而下搜索和自下而上搜索。自下而上搜索应该是大部分人熟悉的搜索方法,一般我们会从一个随机点出发,然后根据任务和空间本身的特点找到符合要求的值或者集合,比如你丢了一块橡皮,通过橡皮滚落的大致轨迹去寻找橡皮的下落,这是属于自下而上的搜索方式。而自上而下的搜索方式则是类似于排除法,它会根据任务和搜索空间本身的特点去排除搜索空间中肯定不是目标的子空间,不断排除,直到停止,那么剩余的空间就是搜索答案,有点类似于收网捕鱼。
Apriori的搜索方式就属于自上而下的搜索方式。虽然 \(\mathcal{I}\) 的幂集的大小大得离谱, 但是也是有章可循的, 我们可以按照项集元素的数量将总的搜索空间给它切成 \(m\) 份(只有一个元素的项集, 只有两个元素的项集,......, 有m个元素的项集),它们的大小分别为 \(\left(\begin{array}{c}m \\ 1\end{array}\right),\left(\begin{array}{c}m \\ 2\end{array}\right), \ldots,\left(\begin{array}{c}m \\ m\end{array}\right)\) 。然后从只有一个元素的项集出发, 不断削减搜索空间, 得到1-频繁项集, 并根据一定的准则根据1-频繁项集推出若干个有两个元素的项集集合, 从而进行迭代。
含有k个元素的项集被称为k-项集(k-itemset),同理,如果该项集恰好又是频繁项集,那么该项集又可称为k-频繁项集
(1) 算法流程
Apriori的做法是从大小为1的项集集合, 该集合被我们称为候选集 \(C_1\) 。我们从候选集 \(C_1\) 出发, 然后通过䇘选得到1-频繁项集 \(L_1\), 连接, 减枝的方法得到大小为 2 候选集 \(C_2\), 其中的䇘选和减枝 两步都能有效缩减搜索空间。
直接从事务集 \(D\) 中提取所有的transaction, 然后找出里面所有不相同的元素就行,记 \(\mathcal{I}=\left\{I_1, I_2, \ldots, I_m\right\}\) 。
然后, 我们需要初始化第一个候选集, 也就是 \(C_1 。 C_1\) 就是 \(\mathcal{I}\) 本身, 对 \(C_1\) 中的每个元素, 计算其在 \(D\) 中的频率, 如果频率小于min_sup,那就删除,最终留下的元素构成集合 \(L_1\) ,这就是我们的1-频繁项集。
接下来我们就需要迭代向前了,让我们的搜索空间从1-项集集合跳到2-项集集合, 这跳跃的过程通过连接完成。
为了方便后续描述, 假设我们已经得到了k-频繁项集的集合 \(L_k\) 了。首先我们需要保证 \(L_k\) 中每个频繁项集内部都已经按照字典序排序了, 然后所有的频繁项集之间两两比较, 如果这两个项集前 \(k-1\) 项全部相同 ( \(L_k\) 也是集合,所以 \(L_k\) 中的所有频繁项集都是两两不同的, 前 \(k-1\) 项全部相同意味着它们的最后一个元素一定不一样),那么将这两个项集取并集然后加入集 合 \(C_{k+1}\) 中。这样一来, 我们就获得了 \(\mathrm{k}+1\)-项集的待选集合了, 但是这个集合由于经过了 \(\left(\begin{array}{c}\left|L_k\right| \\ 2\end{array}\right)\) 次组合挑选, 所以大小可能会很大, 因此, 在连接完成后, 我们有必要进行裁剪来缩小下一轮迭代的搜索空间。
这个地方就需要用到Apriori算法中提出的一个假设了—一个频繁项集的任意子集都是步繁项集,由于我们下一轮迭代的目标就是得到 \(k+1\)-频繁项集,所以我们可以在这里直接把不是频繁项集的项集去除。根据这个假设, 那么那些存在子集为非频繁项集的项集就是非频繁项集,那 么我将其从 \(C_{k+1}\) 中去除。当我们全部去除后,那么裁剪步骤完成,我们得到了下一轮迭代需要用 到的搜索需要用到的候选集 \(C_{k+1}\) 。进入下一个循环。
最终说明一下终止条件:
- 如果当前轮次得到的频繁项集为空, break
- 如果当前轮次得到的频繁项集只有一个元素, 存入结果, break
- 如果候选集筛选后为空, break
- 如果连接后的候选集裁剪后, 为空, break
循环结束或者终止后 (假设迭代了 \(n\) 次),将集合 \(\left\{L_1, L_2, L_3, \ldots, L_n\right\}\) 返回。
(2) 样例
当前的事务集如下:
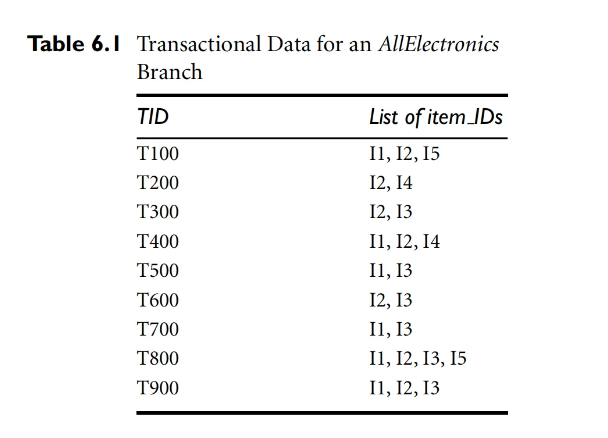
那么请算出各个level的频繁项集。其中,筛选步骤的min_sup为 29 ,也就是只要出现2次以下就筛去。

1.4 缺点
虽然Apriori算法能够有效计算频繁项集, 但是其缺点依旧存在:
- 需要多次扫描数据集:Apriori算法中间有许多步骤都需要对某一个大集合(比如 \(D, L_k\) ) 进行遍历扫描,如果数据量庞大,那么遍历扫描仍然会占据大量的时间。
- 可能会产生庞大的候选集:由于第 \(k\) 迭代的连接过程仍然需要进行 \(\left(\begin{array}{c}\left|L_k\right| /\ 2\end{array}\right)\) 次比较操作, 所以Apriori算法中途产生的候选集的数量依然巨大。
针对Apriori算法的性能瓶颈问题,2000年Jiawei Han等人提出了基于FP树生成频繁项集的FP-growth算法。