支持向量机（2）软间隔对偶性

SVM 是一个非常优雅的算法，具有完善的数学理论，虽然如今工业界用到的不多，但还是决定花点时间去写篇文章整理一下。

本质：SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。为了对数据中的噪声有一定的容忍能力。以几何的角度，在丰富的数据理论的基础上，简化了通常的分类和回归问题。

几何意义：找到一个超平面将特征空间的正负样本分开，最大分隔（对噪音有一定的容忍能力）；

间隔表示：划分超平面到属于不同标记的最近样本的距离之和；

一、软间隔线性SVM

在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，我们应该怎么办？比如下面这个：

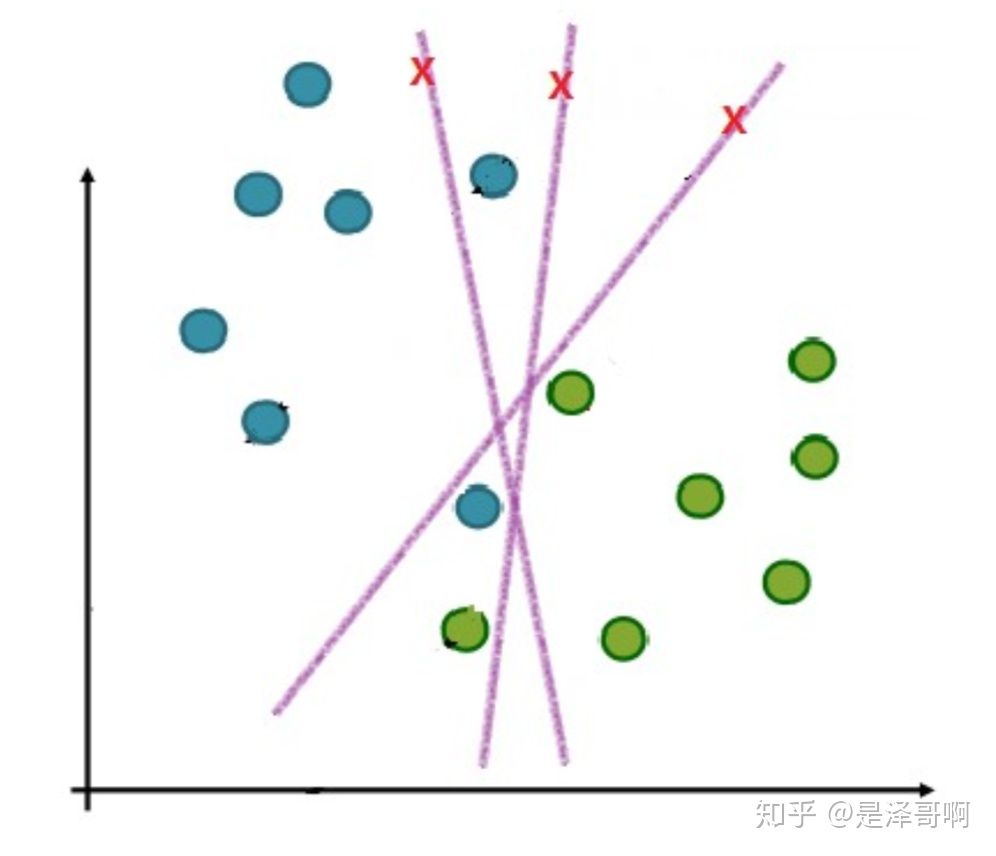
于是我们就有了软间隔，相比于硬间隔的苛刻条件，我们允许个别样本点出现在间隔带里面，比如：

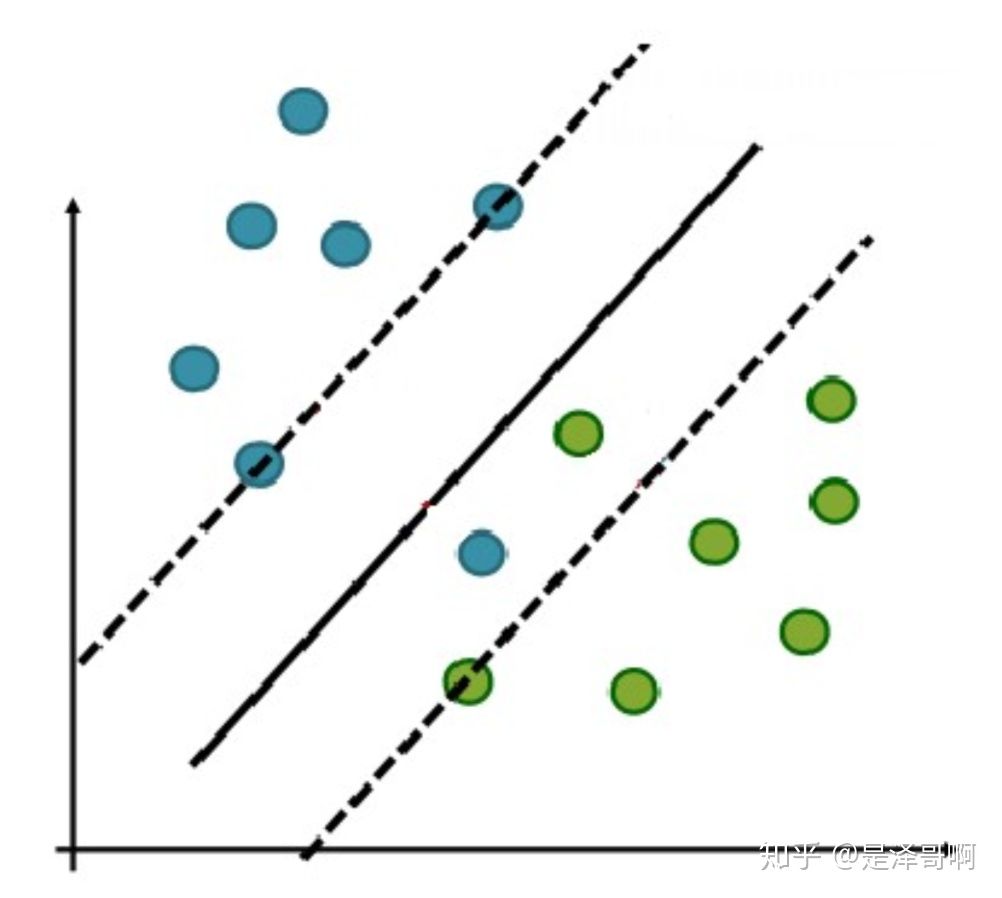
我们允许部分样本点不满足约束条件: \[ 1-y_i\left(w^T x_i+b\right) \leq 0 \] 为了度量这个间隔软到何种程度, 我们为每个样本引入一个松弛变量 \(\xi_i\), 令 \(\xi_i \geq 0\), 且 \(1-y_i\left(w^T x_i+b\right)-\xi_i \leq 0\) 。对应如下图所示:

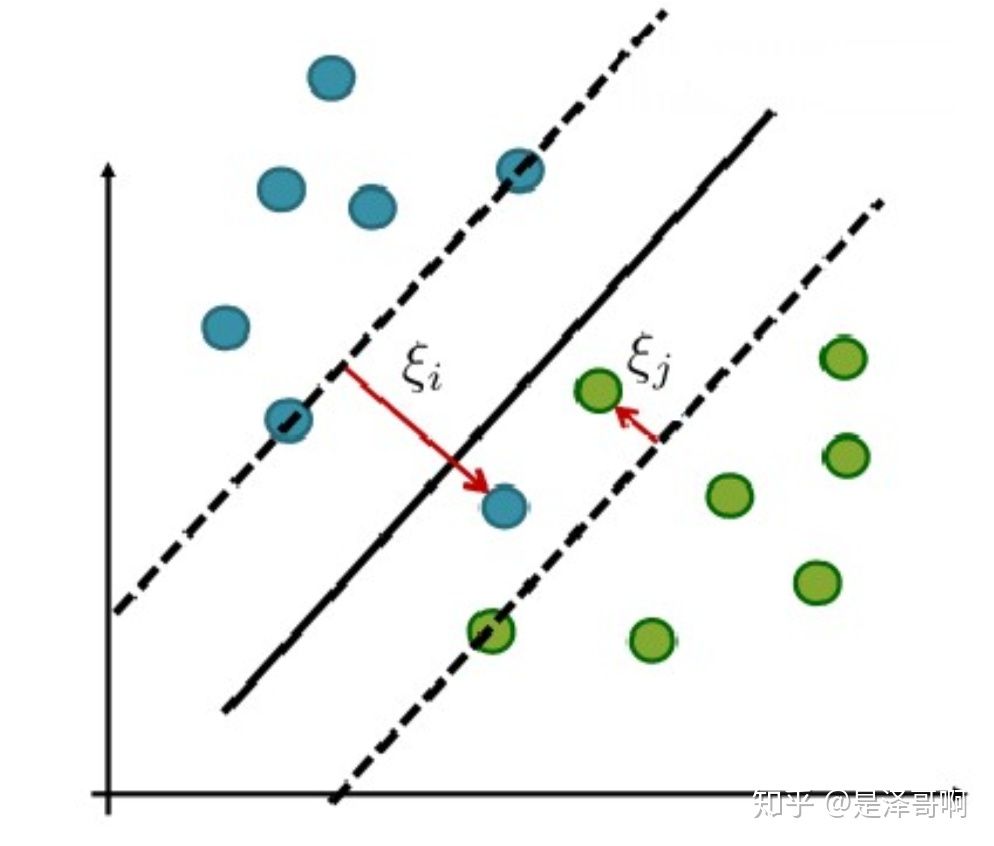
这边要注意一个问题，在间隔内的那部分样本点是不是支持向量？

我们可以由求参数 w 的那个式子可看出，只要\(\lambda > 0\)的点都能够影响我们的超平面，因此都是支持向量。

硬间隔线性SVM的基本型：【凸二次规划问题， 具有全局最小值】 \[ \begin{array}{ll} \min _{w, b} & \frac{1}{2} w^{\top} w \\ \text { s.t. } & y_{i}\left(w^{\top} x_{i}+b\right) \geq 1, \quad i=1,2, \ldots, m \end{array} \] 约束中要求所有的样本都满足 \(y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right) \geq 1\), 也就是让所有的样本都满足 \(y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right)>0\)。 现在我们想对该约束进行一点放松, 我们希望在优化间隔的同时, 允许分类错误的样本出现, 但这类样本应尽可能少: \[ \begin{array}{ll} \min _{w, b} & \frac{1}{2} w^{\top} w+C \sum_{i=1}^{m} \mathbb{I}\left(y_{i} \neq \operatorname{sign}\left(w^{\top} \phi\left(x_{i}\right)+b\right)\right) \\ \text { s.t. } & y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right) \geq 1, \quad \text { 若 } y_{i}=\operatorname{sign}\left(w^{\top} \phi\left(x_{i}\right)+b\right) . \end{array} \] 其中, 优化目标的第一项 \(\frac{1}{2} w^{\top} w\) 源自硬间隔核化 SVM 的基本型, 即优化间隔。优化目标的第二项 中的 \(\mathbb{I}(\cdot)\) 是指示函数, 函数的参数通常是一个条件, 如果条件为真（True）, 则指示函数值为 1 ; 如果条件为假 (False), 则指示函数值为 0 。 \(\sum_{i=1}^{m} \mathbb{I}\left(y_{i} \neq \operatorname{sign}\left(w^{\top} \phi\left(x_{i}\right)+b\right)\right)\) 的含义是统计训练集 \(D\) 中所有预测错误的样本总数。因此, 公式 162 的目标函数是同时优化间隔和最小化训练集预测错误的样本总数, \(C\) 是个可调节的超参数, 用于权衡优化间隔和出现少量分类错误的样本这两个目标。

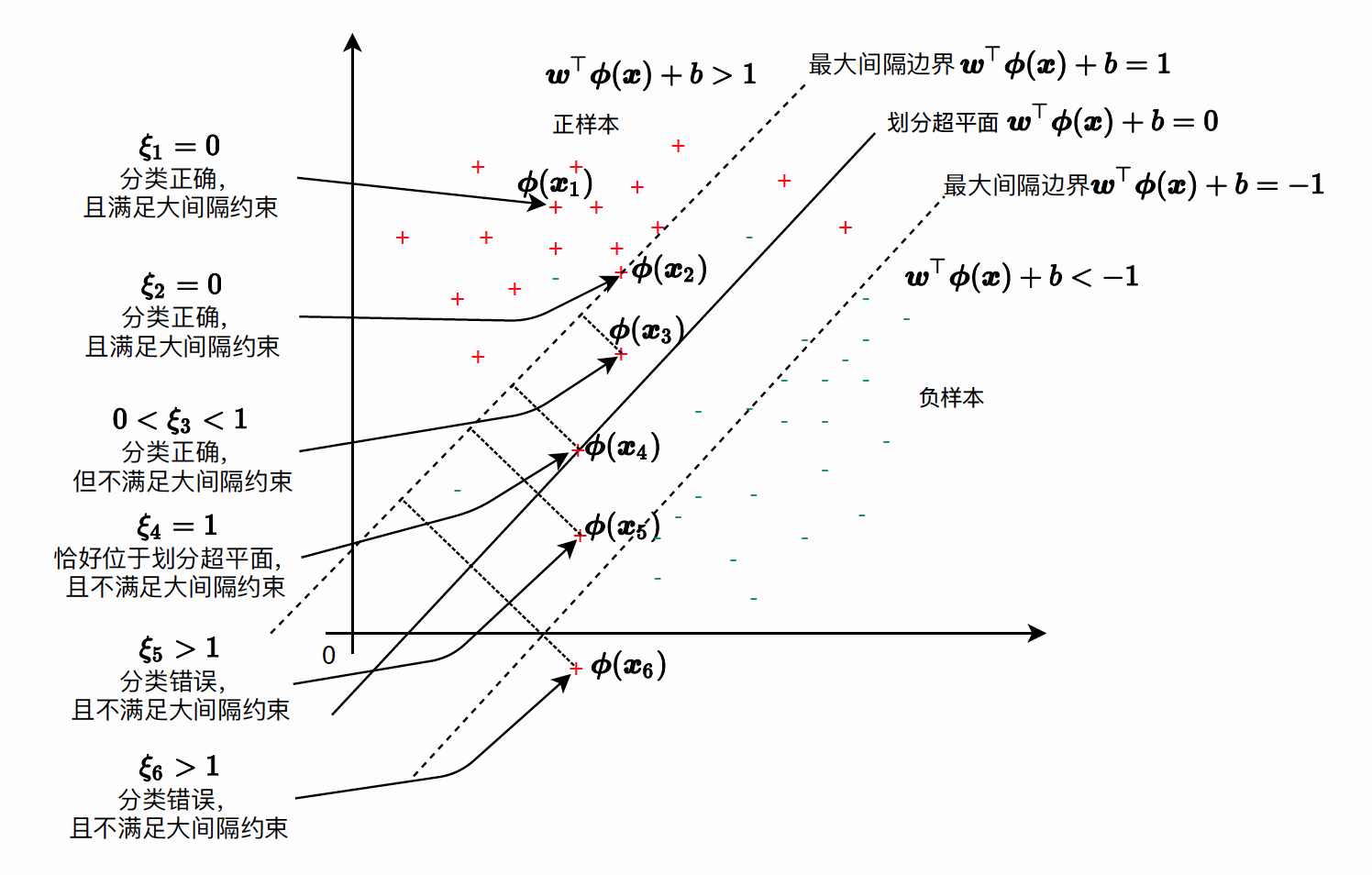
但是, 由于指示函数 \(I(\cdot)\) 不是连续函数, 更不是凸函数, 使得优化问题不再是二次规划问题, 求解起来十分困难, 所以我们需要对其进行简化。另外指示函数没有区分预测错误的不同程度,因此, 我们引入松他变量 (Slack Variable) \(\xi_{i} \in \mathbb{R}\), 用于度量训练集 \(D\) 中第 \(i\) 个样本违背约束的程度。当第 \(i\) 个样本违背约束的程度越大, 松弛变量 \(\xi_{i}\) 的值越大 \[ \xi_{i}:= \begin{cases}0 & \text { 若 } y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right) \geq 1 ; \\ 1-y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right) & \text { 否则. }\end{cases} \] 基于以上定义, 松弛变量 \(\xi_{i}\) 的取值有以下四种情况, 如图 27 所示, 注意图 27 只是示意图, 用于理 解概念, 不表示用图中数据训练得到的分类边界一定是这样: - 当 \(\xi_{i}=0\) 时, 训练集 \(D\) 中第 \(i\) 个样本分类正确 \(h\left(x_{i}\right)=y_{i}\), 且满足大间隔约束 \(y_{i}\left(w^{\top} \phi\left(x_{i}\right)+b\right) \geq 1\); - 当 \(0<\xi_{i}<1\) 时, 训练集 \(D\) 中第 \(i\) 个样本分类正确 \(h\left(x_{i}\right)=y_{i}\), 但是不满足大间隔约束; - 当 \(\xi_{i}=1\) 时, 训练集 \(D\) 中第 \(i\) 个样本恰好位于划分超平面 \(w^{\top} \phi\left(x_{i}\right)+b=0\) 上, 且不满足大间 隔约束; - 当 \(\xi>0\) 时, 训练集 \(D\) 中第 \(i\) 个样本分类错误 \(h\left(x_{i}\right) \neq y_{i}\), 且不满足大间隔约束。

软间隔核化SVM基本型：（合页损失函数）：

\[ \begin{array}{ll} \min _{\boldsymbol{w}, b, \boldsymbol{\xi}} & \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^m \xi_i \\ \text { s.t. } & y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right) \geq 1-\xi_i, \quad i=1,2, \ldots, m \\ & \xi_i \geq 0, \quad i=1,2, \ldots, m . \\ & \xi_i=\max \left(1-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right), 0\right) . \end{array} \] 变为: \[ \begin{aligned} & \min _{\boldsymbol{w}, b, \boldsymbol{\xi}} \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^m \xi_i \\ = & \min _{\boldsymbol{w}, b} \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^m \max \left(1-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right), 0\right) \\ = & \min _{\boldsymbol{w}, b} C \sum_{i=1}^m \max \left(1-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b\right), 0\right)+\frac{1}{2}\|\boldsymbol{w}\|^2 . \end{aligned} \] 令 \(\lambda:=\frac{1}{m C}:\) 合页损失 \[ \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \max \left(1-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_i\right)+b, 0\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2\right. \] 回顾：对数几率回归: \[ \min _{\boldsymbol{w}, b} \frac{1}{m} \sum_{i=1}^m \log \left(1+\exp \left(-y_i\left(\boldsymbol{w}^{\top} \boldsymbol{x}_i+b\right)\right)\right)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2 . \] 软间隔核化SVM对偶性： 软间隔的对偶性是在硬间隔的对偶性对拉格朗日参数添加一个上界。 \[ \begin{array}{ll} \min _{\boldsymbol{\alpha}} & \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)-\sum_{i=1}^m \alpha_i \\ \text { s. t. } & 0 \leq \alpha_i \leq C, \quad i=1,2, \ldots, m, \\ & \sum_{i=1}^m \alpha_i y_i=0 . \end{array} \]