理论基础(4)聚类评价指标
一、聚类算法评价指标
https://zhuanlan.zhihu.com/p/343667804
十分钟掌握聚类算法的评估指标:https://juejin.cn/post/6997913127572471821
前言 【外部评估】+ 【内部指标】
如同之前介绍的其它算法模型一样,对于聚类来讲我们同样会通过一些评价指标来衡量聚类算法的优与劣。在聚类任务中,常见的评价指标有:纯度(Purity)、兰德系数(Rand Index, RI)、F值(F-score)和调整兰德系数(Adjusted Rand Index,ARI)。同时,这四种评价指标也是聚类相关论文中出现得最多的评价方法。下面,我们就来对这些算法一一进行介绍。
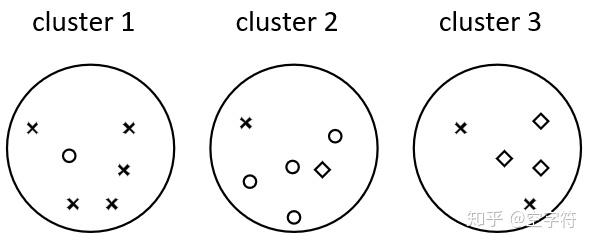
好的聚类算法,一般要求类簇具有:
- 簇内 (intra-cluster) 相似度高
- 簇间 (inter-cluster) 相似度底
一般来说,评估聚类质量有两个标准,内部评估评价指标和外部评估指标。内部评估指标主要基于数据集的集合结构信息从紧致性、分离性、连通性和重叠度等方面对聚类划分进行评价。即基于数据聚类自身进行评估的。
1.1聚类纯度 - 聚类的准确率
在聚类结果的评估标准中, 一种最简单最直观的方法就是计算它的聚类纯度 (purity),别看纯度听起来很陌生, 但实际上和分类问题中的准确率有着异曲同工之妙。因为聚类纯度的总体思想也用聚类正确的样本数除以总的样本 数, 因此它也经常被称为聚类的准确率。只是对于聚类后的结果我们并不知道每个簇所对应的真实类别, 因此需要 取每种情况下的最大值。具体的,纯度的计算公式定义如下: \[ P=(\Omega, \mathbb{C})=\frac{1}{N} \sum_k \max _j\left|\omega_k \cap c_j\right| \] 其中 \(N\) 表示总的样本数; \(\Omega=\left\{\omega_1, \omega_2, \ldots, \omega_K\right\}\) 表示一个个聚类后的簇, 而 \(\mathbb{C}=\left\{c_{1,2}, \ldots c_J\right\}\) 表示正确的类别; \(\omega_k\) 表示聚类后第 \(k\) 个簇中的所有样本, \(c_j\) 表示第 \(j\) 个类别中真实的样本。在这里 \(P\) 的取值范围为 \([0,1]\) ,越大表示 聚类效果越好。
1.2 兰德系数与F值 [同簇混淆矩阵]
在介绍完了纯度这一评价指标后,我们再来看看兰德系数(Rand Index)和F值。虽然兰德系数听起来是一个陌生 的名词, 但它的计算过程却也与准确率的计算过程类似。同时, 虽然这里也有一个叫做值的指标, 并且它的计算 过程也和分类指标中的F值类似, 但是两者却有着本质的差别。说了这么多, 那这两个指标到底该怎么算呢? 同分 类问题中的沘淆矩阵类似,这里我们也要先定义四种情况进行计数,然后再进行指标的计算。
为了说明兰德系数背后的思想,我们还是以图1中的聚类结果为例进行说明(为了方便观察,我们再放一张图在这 里):
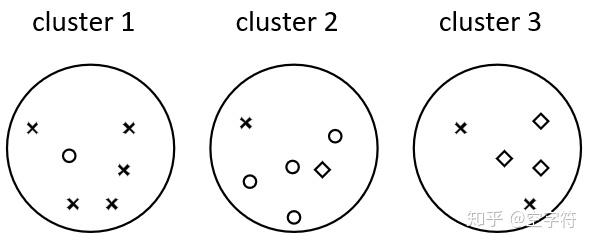
- \(T P\) : 表示两个同类样本点在同一个簇(布袋)中的情况数量;
- \(F P\) : 表示两个非同类样本点在同一个簇中的情况数量;
- \(T N\) : 表示两个非同类样本点分别在两个簇中的情况数量;
- \(F N\) : 表示两个同类样本点分别在两个簇中的情况数量;
由此,我们便能得到如下所示的对混淆矩阵(Pair Confusion Matrix):

有了上面各种情况的统计值,我们就可以定义出兰德系数和F值的计算公式: \[ Precision =\frac{T P}{T P+F P} \]
\[ Recall =\frac{T P}{T P+F N} \]
\[ R I =\frac{T P+T N}{T P+F P+F N+T N} \]
\[ F_\beta =\left(1+\beta^2\right) \frac{\text { Precision } \cdot \text { Recall }}{\beta^2 \cdot \text { Precision }+ \text { Recall }} \]
从上面的计算公式来看, (3)(4) 从形式上看都非常像分类问题中的准确率与F值, 但是有着本质的却别。同时, 在 这里 \(R I\) 和 \(F_\beta\) 的取值范围均为 \([0,1]\) ,越大表示聚类效果越好。
1.3 调整兰德系数(Adjusted Rand index)【归一化】
对于随机结果,RI并不能保证分数接近零。为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德系数(Adjusted rand index)被提出,它具有更高的区分度。
其公式为: \[ \mathrm{ARI}=\frac{\mathrm{RI}-E[\mathrm{RI}]}{\max (\mathrm{RI})-E[\mathrm{RI}]} \] \(A R\) 取值范围为 \([-1,1]\), 值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲, ARI衡量的是两个数据分布 的吻合程度。
优点:
- 对任意数量的聚类中心和样本数, 随机聚类的ARI都非常接近于 0 。
- 取值在 \([-1,1]\) 之间, 负数代表结果不好, 越接近于1越好。
- 对簇的结构不需作出任何假设:可以用于比较聚类算法。
缺点:
- ARI 需要 ground truth classes 的相关知识, ARI需要真实标签, 而在实践中几乎不可用, 或者需要人工 标注者 手动分配(如在监督学习环境中)。
1.4 标准化互信息(NMI, Normalized Mutual Information)
互信息是用来衡量两个数据分布的吻合程度。它也是一有用的信息度量,它是指两个事件集合之间的相关性。互信息越大,词条和类别的相关程度也越大。
1.5 轮廓系数(Silhouette Coefficient)
轮廓系数适用于实际类别信息末知的情况。对于单个样本, 设 \(a\) 是与它同类别中其他样本的平均距离, \(b\) 是与它距离最近不同类别中样本的平均距离, 其轮廓 系数为: \[ s=\frac{b-a}{\max (a, b)} \] 对于一个样本集合, 它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是 \([-1,1]\), 同类别样本距离 越相近, 不同类别样本距离越远, 值越大。当值为负数时, 说明聚类效果很差。
1.6 Calinski-Harabaz指数(Calinski-Harabaz Index)
在真实的分群label不知道的情况下,Calinski-Harabasz可以作为评估模型的一个指标。
Calinski-Harabasz指数通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。从而,CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
优点
- 当簇的密集且分离较好时,分数更高。
- 得分计算很快,与轮廓系数的对比,最大的优势:快!相差几百倍!毫秒级。
缺点
- 凸的簇的CH指数通常高于其他类型的簇。例如,通过 DBSCAN 获得基于密度的簇;所以,不适合基于密度的聚类算法(DBSCAN)。
1.7 戴维森堡丁指数(DBI, Davies-Bouldin Index)
DB指数是计算任意两类别的类内距离平均距离之和除以两聚类中心距离求最大值。DB越小,意味着类内距 离越小同时类间距离越大。零是可能的最低值, 接近零的值表示更好的分区。 \[ \begin{gathered} R_{i j}=\frac{s_{i}+s_{j}}{d_{i j}} \\ D B=\frac{1}{k} \sum_{i=1}^{k} \max _{i \neq j} R_{i j} \end{gathered} \] 其中, \(s_{i}\) 表示簇的每个点与该簇的质心之间的平均距离, 也称为簇直径。 \(d_{i j}\) 表示聚类和的质心之间的距 离。 算法生成的聚类结果越是朝着簇内距离最小(类内相似性最大)和笶间距离最大(类间相似性最小)变化, 那么Davies-Bouldin指数就会越小。 缺点:
- 因使用欧式距离, 所以对于环状分布聚类评测很差。