算法长征-代码随想录

发表于 2021-05-07 更新于 2022-05-19 分类于【draft】工程，数据结构阅读次数：本文字数： 12k 阅读时长 ≈ 22 分钟

一、树状数组

leecode 题目：数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4] 输出: 5

「树状数组」是一种可以动态维护序列前缀和的数据结构，它的功能是：

单点更新update(i, v):把序列 $i$ 位置的数加上一个值$v$，这题 v = 1
区间查询 query(i)： 查询序列[1⋯i] 区间的区间和，即 i 位置的前缀和

修改和查询的时间代价都是 $O(\log n)$，其中 n 为需要维护前缀和的序列的长度。

二、单调栈

通常是一维数组，要==寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置==，此时我们就要想到可以用单调栈了。

单调栈里存放的元素是什么？

单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。
单调栈里元素是递增呢？还是递减呢？

注意一下顺序为从栈头到栈底的顺序，因为单纯的说从左到右或者从前到后，不说栈头朝哪个方向的话，大家一定会越看越懵。
目标列表遍历顺序？ 倒序？正序？

2.1 下一个更大元素

def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
    # 下一个更大的元素：单调栈(不增的不要) + 哈希 
    res = {}
    stack = []
    for num in reversed(nums2): # 倒序？
        while stack and num >= stack[-1]:
            stack.pop()
        res[num] = stack[-1] if stack else -1
        stack.append(num)
    return [res[num] for num in nums1]

2.1 下一个更大元素2（循环数组）又TM是循环

    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 三次逆转
        s = list(nums[::-1])
        res = []
        for num in nums[::-1]:
            while s and s[-1] <= num:
                s.pop()
            if s:
                res.append(s[-1])
            else:
                res.append(-1)
            s.append(num)
        res.reverse()
        return res
"""
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 2n 遍历
        n = len(nums)
        ret = [-1] * n
        stk = list()
        for i in range(n * 2 - 1):
            while stk and nums[stk[-1]] < nums[i % n]:
                ret[stk.pop()] = nums[i % n]
            stk.append(i % n)
        return ret
"""
"""
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 栈留判断
        n = len(nums)
        ans = [-1 for _ in range(n)]
        stack = [0]
        stack2 = []
        for i in range(1, n):
            while stack and nums[i] > nums[stack[-1]]: # ？
                ans[stack[-1]] = nums[i]
                stack.pop() 
            stack.append(i)
        while len(stack) > 1: # 栈顶是最大的保留
            for num in nums: # 从头找？
                if num > nums[stack[-1]]:
                    ans[stack[-1]] = num
                    break
            stack.pop()
        return ans
"""

2.3 每日温度

def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
    # next Geater 
    n = len(temperatures)
    res = [0 for _ in range(n)] 
    stack = [0] # 存的初始索引
    for i in range(1, n): # 正序
        while stack and temperatures[i] > temperatures[stack[-1]]:
            res[stack[-1]] = i - stack[-1]  # stack[-1]
            stack.pop() 
        stack.append(i)
    return res

2.4 接雨水

接雨水是找每个柱子左右两边第一个大于该柱子高度的柱子。

def trap(self, height: List[int]) -> int:
    # 单调栈 左 弹出后 s.top() 中 s.pop()  右 height[i]
    n = len(height)
    stack = [0]
    res = 0
    for i in range(n):
        while stack and height[i] > height[stack[-1]]:
            mid = stack.pop() # 弹一个左面还有的话就是有坑
            if stack:
                high = min(height[stack[-1]], height[i]) - height[mid] 
                # 高 = 左右最小 - 低
                weith = i - stack[-1] - 1 # 宽
                res += weith * high 
        stack.append(i)
    return res

2.5 柱状图的最大矩形

找每个柱子左右两边第一个小于该柱子的柱子。：==栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度==

def largestRectangleArea(self, heights: List[int]) -> int:
    # 单调栈 左右两边都可以用
    heights.insert(0, 0)
    heights.append(0)
    stack = [0]
    ans = heights[0]
    for i in range(1, len(heights)):
        while stack and heights[i] < heights[stack[-1]]:
            mid = stack.pop()
            if stack: # 存在左右最小
                weith = i - stack[-1] - 1
                # high = max(heights[i], heights[stack[-1]])
                ans = max(ans, heights[mid] * weith)
        stack.append(i)
    return ans

三、单调队列

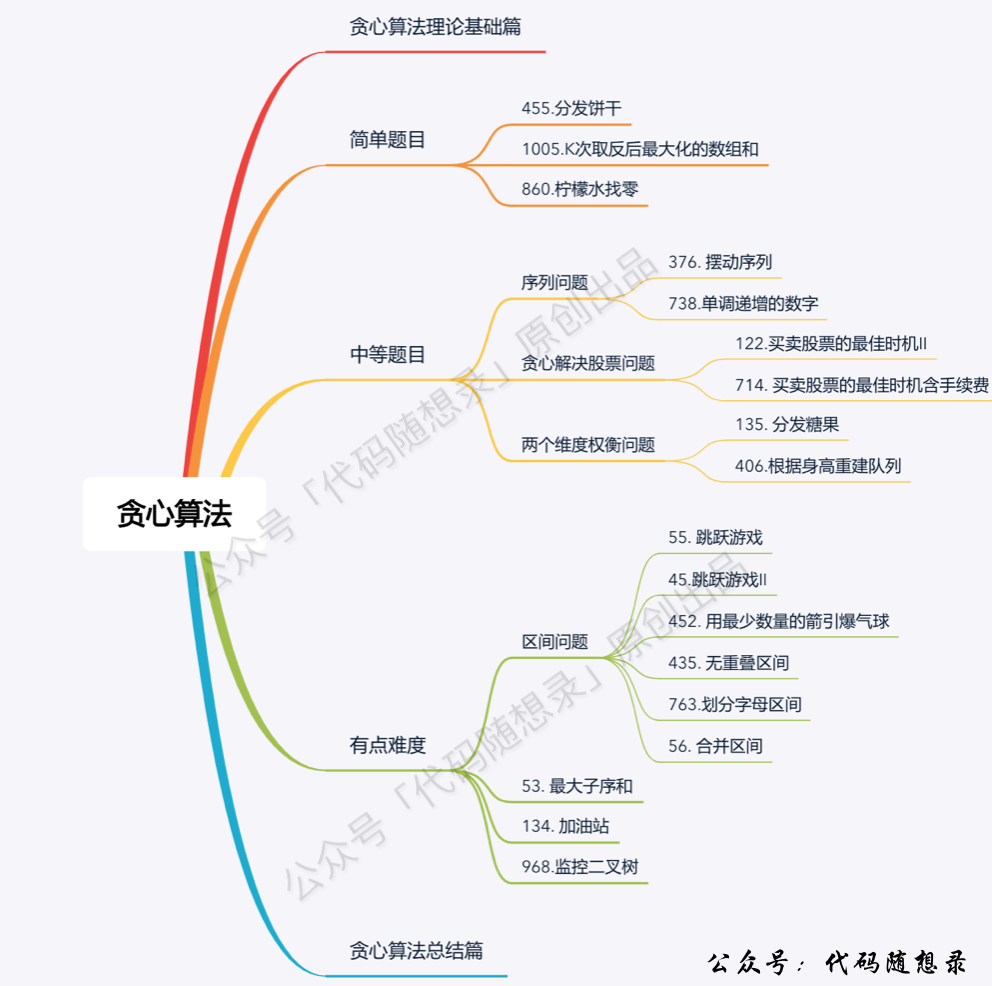
贪心算法大纲

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

贪心一般解题步骤

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

首先，动态规划问题的一般形式就是==求最值==。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。求解动态规划的核心问题是穷举。首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「==备忘录」或者「DP table」==来优化穷举过程，避免不必要的计算。而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的「状态转移方程」，才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我研究出来的一个思维框架，辅助你思考状态转移方程：

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

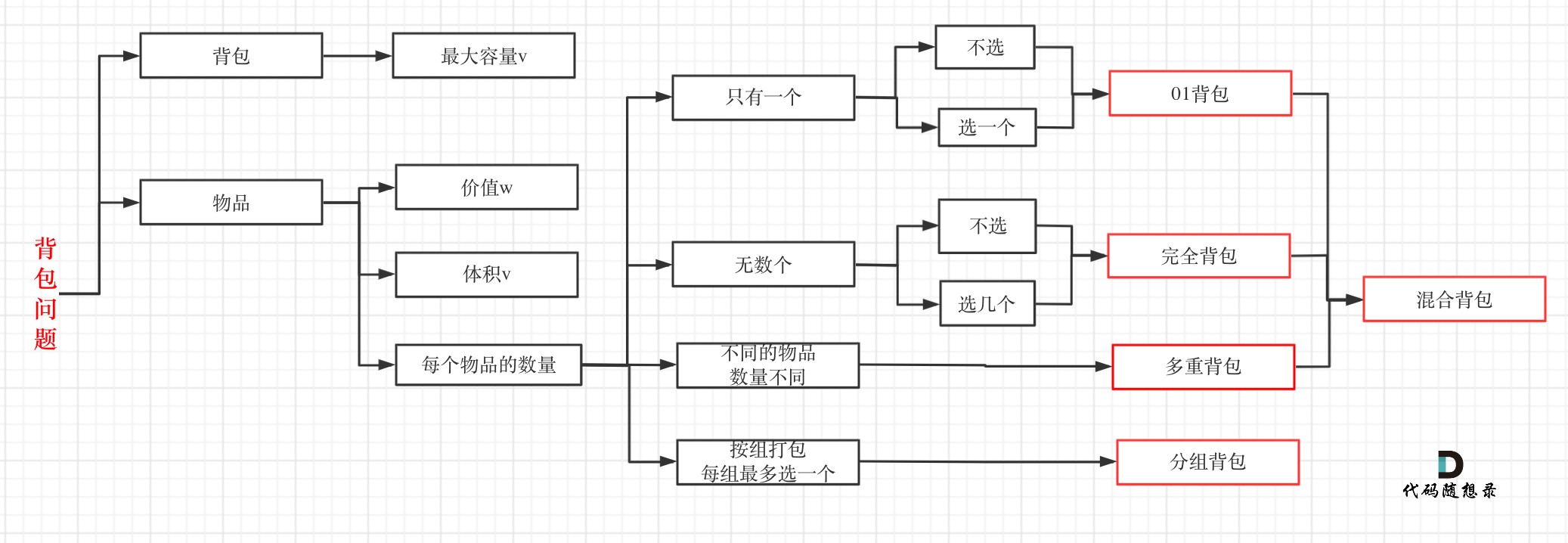
5.1 背包问题

https://leetcode-cn.com/problems/coin-change/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-wan-q-80r7/

1、确定dp数组以及下标的含义

2、确定递推公式

3、dp数组如何初始化

最大长度

递推等号左侧要初始化

4、确定遍历顺序

滚动数组

5、举例推导dp数组

5.1.1 背包递推公式

问==能否装满背包==（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

==问装满背包有几种方法==：dp[j] += dp[j - nums[i]] ，对应题目如下：

动态规划：494.目标和(opens new window)
动态规划：518. 零钱兑换 II(opens new window)
动态规划：377.组合总和Ⅳ(opens new window)

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。
动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满==最大价值==：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

动态规划：474.一和零

问装满背包所有物品的==最小个数==：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

5.1.2 遍历顺序

01背包

在动态规划：关于01背包问题，你该了解这些！ (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

和动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的，大家需要注意！

完全背包

说完01背包，再看看完全背包。

在动态规划：关于完全背包，你该了解这些！ (opens new window)中，讲解了纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求==组合数==就是外层for循环遍历物品，内层for遍历背包。

如果==求排列数==就是外层for遍历背包，内层for循环遍历物品。

5.2 子序列问题

动态规划：最长递增子序列

# 子序列 
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        dp = [1] * len(nums)
        result = 0
        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
            result = max(result, dp[i]) #取长的子序列
        return result

def lenLongestFibSubseq(self, A: List[int]) -> int:
    # 基本顺序是 k，i，j 或者 A[k] = A[j] - A[i]
    n = len(A)
    dic = {}
    # 创建索引字典，提速
    for ind,val in enumerate(A):
        dic[val] = ind
    # 初始化，行代表的是i，不需要取到n-1，为了给j留出位置
    # 初始为2，只要包含了 j i 位置，则意味着已经有了2个数字。
    dp = [[2]*n for _ in range(n-1)]
    ret = 0
    # 因此i只能取到n-2，给j留出空间
    for i in range(1,n-1):
        # j从i+1开始，毕竟j在i后面
        for j in range(i+1,n):
            diff = A[j] - A[i]
            if diff in dic and dic[diff] < i:
                k = dic[diff]
                dp[i][j] = dp[k][i] + 1 # 这个1，代表着k位置数字
                ret = max(ret,dp[i][j])
    return ret

动态规划：最长重复子数组

class Solution:
    def findLength(self, A: List[int], B: List[int]) -> int:
        dp = [0] * (len(B) + 1)
        result = 0
        for i in range(1, len(A)+1):
            for j in range(len(B), 0, -1):
                if A[i-1] == B[j-1]:
                    dp[j] = dp[j-1] + 1
                else:
                    dp[j] = 0 #注意这里不相等的时候要有赋0的操作
                result = max(result, dp[j])
        return result

动态规划：最长公共子序列、动态规划：不相交的线

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 最长子序列 
        m, n = len(text1), len(text2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                if text2[j-1] == text1[i-1]:
                    dp[i][j] = dp[i-1][j-1] +1 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

动态规划：最大子序和【贪心】【动态规划】

def maxSubArray(self, nums: List[int]) -> int:
    # 为什么dp[-1]不是最大？需要res
    # dp[i] 以i结尾的最大子数组和
    n = len(nums)
    if n == 0:
        return 0
    dp = [0] * (n)
    dp[0] = nums[0]
    for i in range(1, n):
        dp[i] = max(dp[i-1]+nums[i], nums[i])
    return max(dp)

动态规划：判断子序列【双指针】

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        n, m = len(s), len(t)
        i = j = 0
        while i < n and j < m:
            if s[i] == t[j]:
                i += 1
            j += 1
        return i == n

# dp[i][j] : word1[i-1], word1[j-1] 最少步数
# word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况 *  min(dp[i-1][j], dp[i][j-1])+1  
  def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(n+1):
            dp[0][i] = i
        for j in range(m+1):
            dp[j][0] = j
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1])+1 # , dp[i-1][j-1]+1
        return dp[-1][-1]

# 中心扩展法
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 枚举+中心扩展法
        def extendCenter(left, right):
            while 0 <= left and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            # 返回的为while不成立的值
            return left+1, right-1 
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = extendCenter(i,i)
            left2, right2 = extendCenter(i,i+1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start:end+1]

def longestPalindrome(self, s: str) -> str:
    # dp[i][j]: 是否是回文 dp[i+1][j-1] -> dp[i][j]
    # 返回的子串，不是数字 不能记录长度
    n = len(s)
    dp = [[False] * n for _ in range(n)] # 右上为1
    for i in range(n):
        dp[i][i] = True
    begin = 0
    maxlen = 0
    # 判断是否是回文子串中，如果是则记录begin and len
    for i in range(n-1, -1,-1):
        for j in range(i,n):
            if s[i] == s[j]:
                if j - i <=1:
                    dp[i][j] = True
                elif dp[i+1][j-1]:
                    dp[i][j] = True
            
            if dp[i][j] and j - i + 1 > maxlen:
                maxlen = j - i + 1
                begin = i

    return s[begin:begin+maxlen]

Manacher 算法

Manacher 算法是在线性时间内求解最长回文子串的算法。在本题中，我们要求解回文串的个数，为什么也能使用 Manacher 算法呢？这里我们就需要理解一下 Manacher 的基本原理。

奇偶长度处理： abaaabaa 会被处理成 #a#b#a#a##a#b#a#a#
==$f(i)$ 来表示以 s 的第 i 位为回文中心，可以拓展出的最大回文半径（包括 # ）==，那么$ f(i) - 1$就是以 i 为中心的最大回文串长度。
利用已经计算出来的状态来更新 f(i）：回文右端点rm ：i + f(i) - 1

动态规划：最长回文子序列

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 最大回文长度
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 and j - i >=2
        n = len(s)
        dp = [[0] * i +[1] * (n-i) for i in range(n)] # 从定义出发 右上三角 = 1 有意义
        for i in range(n-1,-1,-1):
            for j in range(i+1,n): # j - i >=2
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2 
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])                
        return dp[0][n-1]

class Solution:
    def minCut(self, s: str) -> int:
        # 动态规划1:判断回文
        n = len(s)
        g = [[True] * n for _ in range(n)]

        for i in range(n - 1, -1, -1):
            for j in range(i + 1, n):
                g[i][j] = (s[i] == s[j]) and g[i + 1][j - 1]
        # 
        f = [float("inf")] * n
        for i in range(n):

            if g[0][i]:
                f[i] = 0
            else:
                for j in range(i):
                    if g[j + 1][i]:
                        # （0, j) + (j+1, i)
                        f[i] = min(f[i], f[j] + 1)
        
        return f[n - 1]

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        # 动态规划
        dic, res = dict(), 0
        for num in nums:
            if num not in dic:
                left, right = dic.get(num - 1, 0), dic.get(num + 1,0)
                cur = 1 + left +right
                if res < cur:
                    res = cur
                dic[num] = cur
                dic[num - left] = cur
                dic[num + right] = cur
        return res

5.3 打家劫舍问题

5.4 股票问题

动态规划：121.买卖股票的最佳时机(opens new window) 股票只能买卖一次，问最大利润
动态规划：122.买卖股票的最佳时机II(opens new window) 可以多次买卖股票，问最大收益。
动态规划：123.买卖股票的最佳时机III(opens new window) 最多买卖两次，问最大收益。
动态规划：188.买卖股票的最佳时机IV(opens new window) 最多买卖k笔交易，问最大收益。
动态规划：309.最佳买卖股票时机含冷冻期(opens new window) 可以多次买卖但每次卖出有冷冻期1天。
动态规划：714.买卖股票的最佳时机含手续费(opens new window) 可以多次买卖，但每次有手续费。

5.5 编辑距离问题

判断子序列

动态规划：392.判断子序列 (opens new window)给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

这道题目其实是可以用双指针或者贪心的的，但是我在开篇的时候就说了这是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

状态转移方程：

1 2	if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; else dp[i][j] = dp[i][j - 1];

不同的子序列

动态规划：115.不同的子序列 (opens new window)给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

本题虽然也只有删除操作，不用考虑替换增加之类的，但相对于动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了。

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为 dp[i - 1] [j - 1]

一部分是不用s[i - 1]来匹配，个数为 dp[i - 1] [j]

if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

动态规划：583.两个字符串的删除操作 (opens new window)给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

本题和动态规划：115.不同的子序列 (opens new window)相比，其实就是两个字符串可以都可以删除了，情况虽说复杂一些，但整体思路是不变的。

当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1] [j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1] [j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

动态规划：72.编辑距离 (opens new window)给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

编辑距离终于来了，有了前面三道题目的铺垫，应该有思路了，本题是两个字符串可以增删改，比动态规划：判断子序列 (opens new window)，动态规划：不同的子序列 (opens new window)，动态规划：两个字符串的删除操作 (opens new window)都要复杂的多。

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
- 不操作
if (word1[i - 1] != word2[j - 1])
- 增
- 删
- 换

也就是如上四种情况。

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1] [j - 1]，即dp[i][j] = dp[i - 1] [j - 1];

在整个动规的过程中，最为关键就是正确理解dp[i] [j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i - 1] [j] + 1;

操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是添加元素，删除元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word2添加一个元素d，也就是相当于word1删除一个元素d，操作数是一样！

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1] [j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i] [j] = min({dp[i - 1] [j - 1], dp[i - 1] [j], dp[i][j - 1]}) + 1;

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

==让字符串成为最小回文==

https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/

六、回溯法

一个决策树的遍历过程（回溯法）：一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会通过在上一步进行一些变化抛弃该解，即回溯并且再次尝试。

回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等