支持向量机（1）硬间隔对偶性

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 6.6k 阅读时长 ≈ 12 分钟

SVM 是一个非常优雅的算法，具有完善的数学理论，虽然如今工业界用到的不多，但还是决定花点时间去写篇文章整理一下。

本质：SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。为了对数据中的噪声有一定的容忍能力。以几何的角度，在丰富的数据理论的基础上，简化了通常的分类和回归问题。

几何意义：找到一个超平面将特征空间的正负样本分开，最大分隔（对噪音有一定的容忍能力）；

间隔表示：划分超平面到属于不同标记的最近样本的距离之和；

【机器学习】支持向量机 SVM（非常详细）

一、支持向量

  • https://zhuanlan.zhihu.com/p/52168498

【机器学习】支持向量机 SVM（非常详细）:https://zhuanlan.zhihu.com/p/77750026

KKT条件：判断不等式约束问题是否为最优解的必要条件

1.1 线性可分

首先我们先来了解下什么是线性可分。

img

在二维空间上, 两类点被一条直线完全分开叫做线性可分。严格的数学定义是: \(D_0\) 和 \(D_1\) 是 \(\mathrm{n}\) 维欧氏空间中的两个点集。如果存在 \(\mathrm{n}\) 维向量 \(\mathrm{w}\) 和实数 \(\mathrm{b}\), 使得所有属于 \(D_0\) 的点 \(x_i\) 都有 \(w x_i+b>0\) ， 而对于所有属于 \(D_1\) 的点 \(x_j\) 则有 \(w x_j+b<0\) ， 则我们称 \(D_0\) 和 \(D_1\) 线性可分。

1.2 最大间隔超平面

从二维扩展到多维空间中时, 将 \(D_0\) 和 \(D_1\) 完全正确地划分开的 \(w x+b=0\) 就成了一个超平面。 为了使这个超平面更具鲁棒性, 我们会去找最佳超平面, 以最大间隔把两类样本分开的超平面, 也称之为最大 间隔超平面。

  • 两类样本分别分割在该超平面的两侧；
  • 两侧距离超平面最近的样本点到超平面的距离被最大化了。【附近点】

1.3 支持向量 【距离超平面最近的点】

img

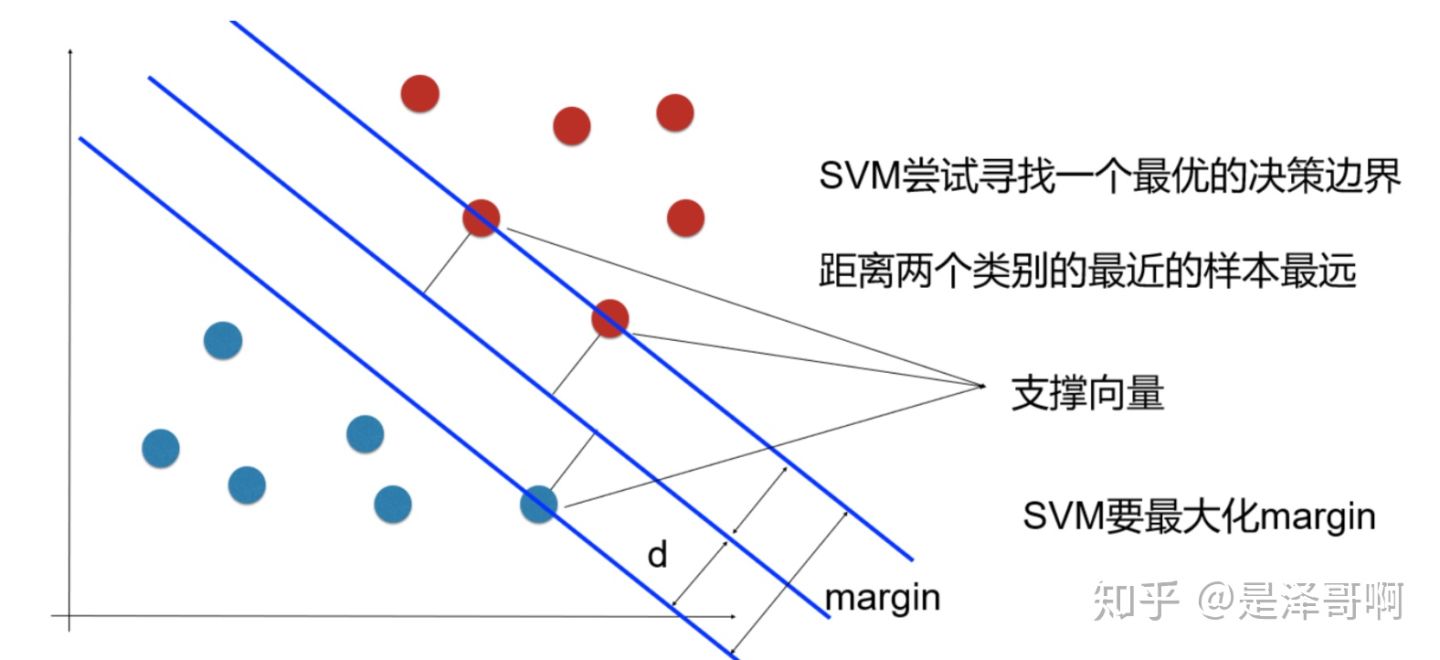
样本中距离超平面最近的一些点，这些点叫做支持向量。

1.4 SVM 最优化问题

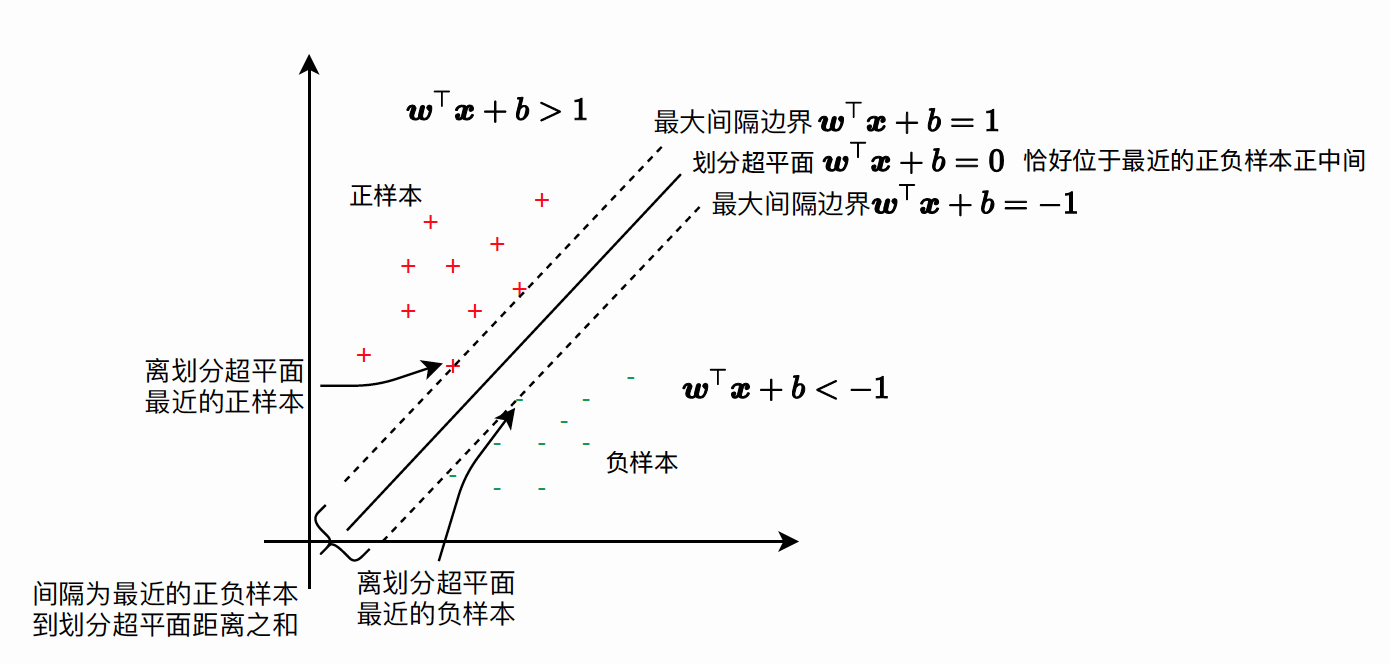
SVM 想要的就是找到各类样本点到超平面的距离最远, 也就是找到最大间隔超平面。任意超平面可以用下面这个 线性方程来描述： \[ w^T x+b=0 \] 二维空间点 \((x, y)\) 到直线 \(A x+B y+C=0\) 的距离公式是: \[ \frac{|A x+B y+C|}{\sqrt{A^2+B^2}} \] 扩展到 \(\mathbf{n}\) 维空间后, 点 \(x=\left(x_1, x_2 \ldots x_n\right)\) 到直线 \(w^T x+b=0\) 的距离为: \[ \frac{\left|w^T x+b\right|}{\|w\|} \] 其中 \(\|w\|=\sqrt{w_1^2+\ldots w_n^2}\) 。 如图所示，根据支持向量的定义我们知道, 支持向量到超平面的距离为 \(d\) ，其他点到超平面的距离大于 \(d\) 。

img

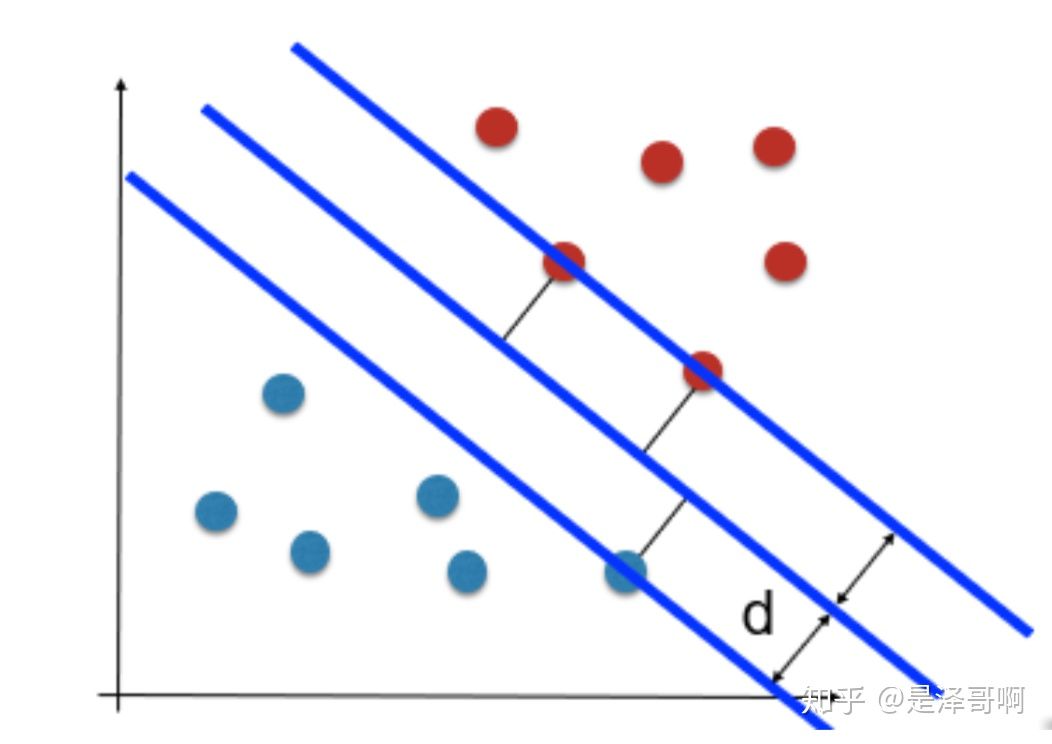
于是我们有这样的一个公式： \[ \left\{\begin{array}{l} \frac{w^T x+b}{\|w\|} \geq d \quad y=1 \\ \frac{w^T x+b}{\|w\|} \leq-d \quad y=-1 \end{array}\right. \] 将两个方程合并, 我们可以简写为: \[ y\left(w^T x+b\right) \geq 1 \] 至此我们就可以得到最大间隔超平面的上下两个超平面：

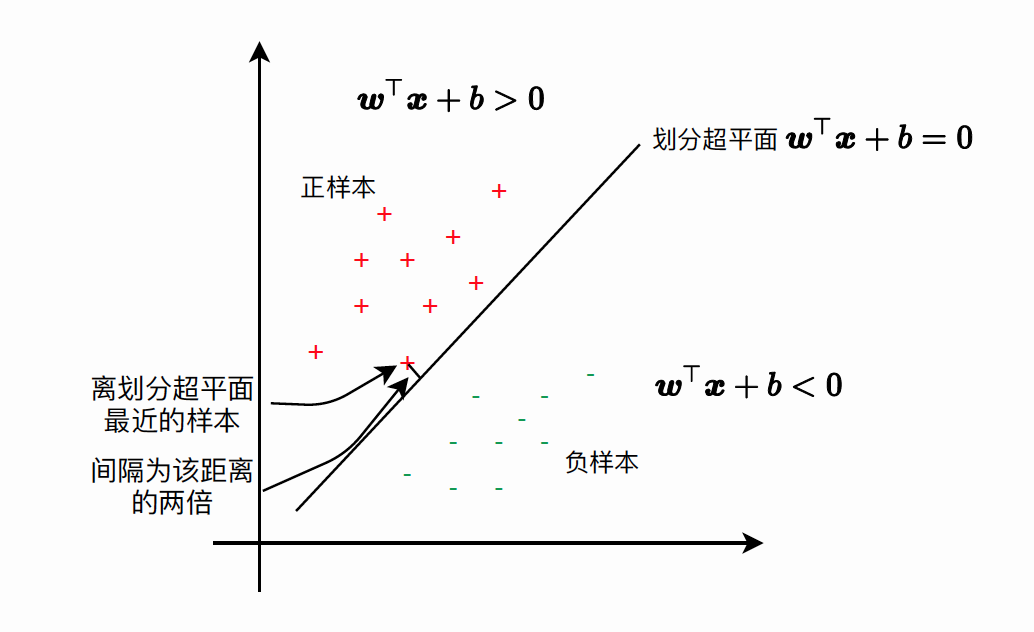
image-20220409203050568

间隔：训练集中离划分超平面最近的样本到划分超平面距离的两倍。有了间隔的定义，划分超平面“离正负样本都比较远”这一目标可以等价描述为正负样本里划分超平面的距离尽可能远。即让离划分超平面最近的样本到划分超平面距离尽可能远。优化目标： \[ \begin{aligned} \max _{w, b} \gamma &=\max _{w, b}\left(2 \min _{i} \frac{1}{\|w\|}\left|w^{\top} x_{i}+b\right|\right) \\ &=\max _{w, b} \min _{i} \frac{2}{\|w\|}\left|w^{\top} x_{i}+b\right| \end{aligned} \] 简化过程：

  • 缩放：为了简化优化问题, 我们可以通过调整 \((w, b)\) 使得： \[ \min _{i}\left|w^{\top} x_{i}+b\right|=1 . \]

  • 标签替换绝对值： \[ s.t. \min _{i} y_{i}\left(w^{\top} x_{i}+b\right)=1 \]

  • 简化约束条件【反正法】

硬间隔线性SVM的基本型：

\[ \begin{array}{ll} \min _{w, b} & \frac{1}{2} w^{\top} w \\ \text { s.t. } & y_{i}\left(w^{\top} x_{i}+b\right) \geq 1, \quad i=1,2, \ldots, m \end{array} \]

image-20220423163130805

二次规划是指目标函数是二次函数，约束是线性不等式约束的一类优化问题 + 凸函数

二、硬间隔线性SVM对偶型

2.1 数学原理

本科高等数学学的拉格朗日程数法是等式约束优化问题: \[ \begin{gathered} \min f\left(x_1, x_2, \ldots, x_n\right) \\ \text { s.t. } \quad h_k\left(x_1, x_2, \ldots, x_n\right)=0 \quad k=1,2, \ldots, l \end{gathered} \] 我们令 \(L(x, \lambda)=f(x)+\sum_{k=1}^l \lambda_k h_k(x)\), 函数 \(L(x, y)\) 称为 Lagrange 函数, 参数 \(\lambda\) 称为 Lagrange 乘子没有非负 要求。 利用必要条件找到可能的极值点: \[ \begin{cases}\frac{\partial L}{\partial x_i}=0 & i=1,2, \ldots, n \\ \frac{\partial L}{\partial \lambda_k}=0 & k=1,2, \ldots, l\end{cases} \] 具体是否为极值点需根据问题本身的具体情况检验。这个方程组称为等式约束的极值必要条件。等式约束下的 Lagrange 乘数法引入了 \(l\) 个 Lagrange 乘子, 我们将 \(x_i\) 与 \(\lambda_k\) 一视同仁, 把 \(\lambda_k\) 也看作优化变 量, 共有 \((n+l)\) 个优化变量。

（1）写成约束优化问题的基本型

\[ \begin{array}{ll} \min _{w, b} & \frac{1}{2} w^{\top} w \\ \text { s.t. } & 1-y_{i}\left(w^{\top} x_{i}+b\right) \leq 0, \quad i=1,2, \ldots, m \end{array} \]

（2） 构建基本型的拉格朗日函数

\[ \mathcal{L}(w, b, \alpha):=\frac{1}{2} w^{\top} w+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(w^{\top} x_{i}+b\right)\right) \]

（3）交换min, max顺序

解得最优解 \(u^{\star}\) 。这样两层优化问题将变为一层最大化（max）问题, 问题难度大大降低, 称为对偶问题 (Dual Problem) :【对偶问题是原问题的下界】

  • \[ \max _{\alpha}, \beta \min _{u} \mathcal{L}(u, \alpha, \beta) \leq \min _{u} \max _{\alpha}, \beta \mathcal{L}(u, \alpha, \beta) \]

  • 硬间隔线性SVM满足Slater条件， 因此原问题和对偶问题等价

\[ \begin{array}{cl} \max _{\alpha} \min _{w, b} & \frac{1}{2} w^{\top} w+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(w^{\top} x_{i}+b\right)\right) \\ \text { s.t. } & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m . \end{array} \]

首先计算 \(w\) 的最优值, 令 \(\frac{\partial \mathcal{L}}{\partial w}=\mathbf{0}\) \[ \begin{aligned} \frac{\partial \mathcal{L}}{\partial w} &=\frac{\partial}{\partial w}\left(\frac{1}{2} w^{\top} w+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(w^{\top} x_{i}+b\right)\right)\right) \\ &=w+\sum_{i=1}^{m} \alpha_{i}\left(-y_{i} x_{i}\right) \\ &=w-\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i} \\ &=\mathbf{0} \end{aligned} \]

可以解得最优值\(w\) \[ w^{\star}=\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i} \] 然后计算 \(b\) 的最优值, 令 \(\frac{\partial \mathcal{L}}{\partial b}=0\) \[ \begin{aligned} \frac{\partial \mathcal{L}}{\partial b} &=\frac{\partial}{\partial b}\left(\frac{1}{2} w^{\top} w+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(w^{\top} x_{i}+b\right)\right)\right) \\ &=\sum_{i=1}^{m} \alpha_{i}\left(-y_{i}\right) \\ &=-\sum_{i=1}^{m} \alpha_{i} y_{i} \\ &=0 \end{aligned} \] 可以得到一个等式 \(b^{\star}\) \[ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \] 注意到这里并没有给出最优值 \(b^{\star}\) 应该是多少, 而是一个等式, 该等式是一个约束项, 而最优值通过后面的 KKT 条件的互补松弛可以计算得到。

硬性间隔线性SVM的对偶型：

\[ \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{\top} x_{j}-\sum_{i=1}^{m} \alpha_{i} \\ \text { s.t. } & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \\ & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \end{array} \]

（4）利用KKT条件得到主问题的最优解

KKT 条件是指优化问题在最优处（包括基本型的最优值，对偶问题的最优值）必须满足的条件。

线性支持向量机的 KKT 条件: - 主问题可行: \(g_{i}\left(u^{\star}\right)=1-y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right) \leq 0\) ； - 对偶问题可行: \(\alpha_{i}^{\star} \geq 0\); - 主变量最优: \(w^{\star}=\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}, \sum_{i=1}^{m} \alpha_{i} y_{i}=0\); - 互补松弛: \(\alpha_{i}^{\star} g_{i}\left(u^{\star}\right)=\alpha_{i}^{\star}\left(1-y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right)\right)=0\) ；

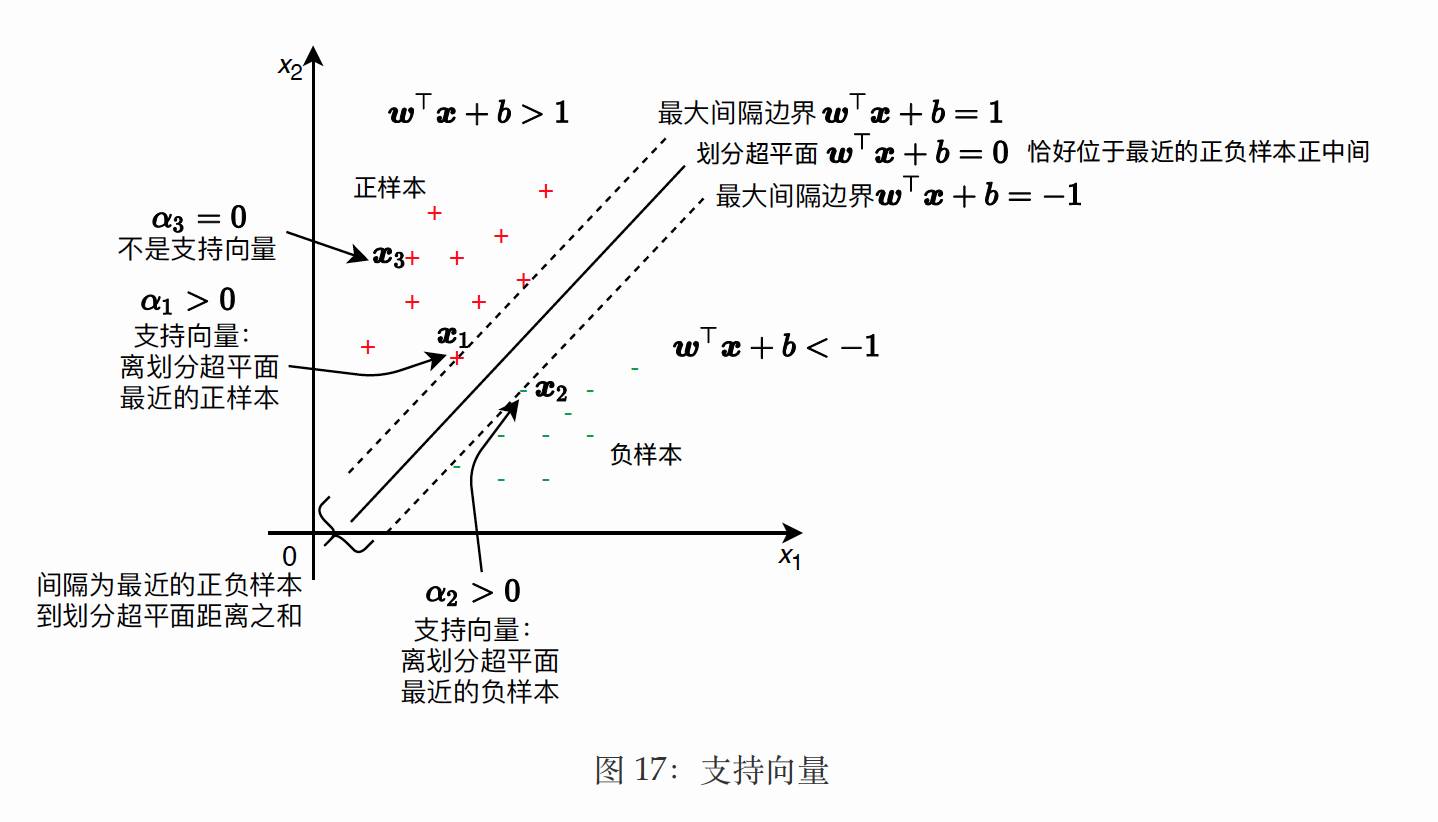
根据 KKT 条件中的 \(\alpha_{i}^{\star} \geq 0\), 我们可以根据 \(\alpha_{i}^{\star}\) 的取值将训练集 \(D\) 中所有的样本分成两类, 如 图 17 所示。

  • 如果 \(\alpha_{i}^{\star}>0\), 对应的样本称为支持向量 (Support Vector), 根据 \(\alpha_{i}^{\star}\left(1-y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right)\right)=0\) , 那么一定有 \(y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right)=1\), 该样本是距离划分超平面最近的样本, 位于最大间隔边界 （见第 \(2.3\) 节）;
  • 如果 \(\alpha_{i}^{\star}=0\), 对应的样本不是非支持向量, 那么有 \(y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right) \geq 1\), 该样本不一定是距离 划分超平面最近的样本, 位于最大间隔边界或之外。

image-20220409212350705

结论：

  • 参数 w， b 仅由支持向量决定，与训练集的其他样本无关；
  • 对偶性是非参数模型，预测阶段不仅需要\(\alpha_{i}\)参数，还支持向量；

\[ \begin{aligned} &h(x):=\operatorname{sign}\left(w^{\star \top} x+b^{\star}\right) \quad \text { （硬间隔线性 SVM 的基本型的假设函数） }\\ &=\operatorname{sign}\left(\sum_{i \in S V} \alpha_{i}^{\star} y_{i} x_{i}^{\top} x+b^{\star}\right) \text {.(硬间隔线性 SVM 的对偶型的假设函数） } \end{aligned} \]

2.2 SVM优化方法

SMO算法求解

我们可以看出来这是一个二次规划问题, 问题规模正比于训练样本数, 我们常用 SMO(Sequential Minimal Optimization) 算法求解。

SMO(Sequential Minimal Optimization), 序列最小优化算法【基于坐标下降算法】, 其核心思想非常简单: 每次只优化一个参数, 其他参数先固定住, 仅求当前这个优化参数的极值。我们来看一下 SMO 算法在 SVM 中的 应用。

我们刚说了 SMO 算法每次只优化一个参数, 但我们的优化目标有约束条件: \(\sum_{i=1}^n \lambda_i y_i=0\), 没法一次只变动一个 参数。所以我们选择了一次选择两个参数。具体步骤为：

  1. 选择两个需要更新的参数 \(\lambda_i\) 和 \(\lambda_j\), 固定其他参数。于是我们有以下约束: 这样约束就变成了:

\[ \lambda_i y_i+\lambda_j y_j=c \quad \lambda_i \geq 0, \lambda_j \geq 0 \]

其中 \(c=-\sum_{k \neq i, j} \lambda_k y_k\), 由此可以得出 \(\lambda_j=\frac{c-\lambda_i y_i}{y_j}\) ，也就是说我们可以用 \(\lambda_i\) 的表达式代替 \(\lambda_j\) 。这样就相当 于把目标问题转化成了仅有一个约束条件的最优化问题, 仅有的约束是 \(\lambda_i \geq 0\) 。

  1. 对于仅有一个约束条件的最优化问题, 我们完全可以在 \(\lambda_i\) 上对优化目标求偏导, 令导数为零, 从而求出变量 值 \(\lambda_{i_{\text {new }}}\) ，然后根据 \(\lambda_{\text {inew }}\) 求出 \(\lambda_{j_{\text {new }}}\) 。
  2. 多次迭代直至收敛。通过 SMO 求得最优解 \(\lambda^*\) 。