线性模型(3)正则化
一、正则化 L1和L2
- 本质其实是为了模型参数服从某一分布;
- 正则化之所以能够降低过拟合的原因在于,正则化是结构风险最小化的一种策略实现;
为什么希望参数具有稀疏性?
相当于对模型进行了一次特征选择,只留下比较重要的特征,提高模型的泛化能力;
正则化是一个通用的算法和思想,所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。在经验风险最小化的基础上(也就是训练误差最小化),尽可能采用简单的模型,可以有效提高泛化预测精度。如果模型过于复杂,变量值稍微有点变动,就会引起预测精度问题。正则化之所以有效,就是因为其降低了特征的权重,使得模型更为简单。
正则化一般会采用 L1 范式或者 L2 范式, 其形式分别为 \(\Phi(w)=\|x\|_1\) 和 \(\Phi(w)=\|x\|_2 。\)
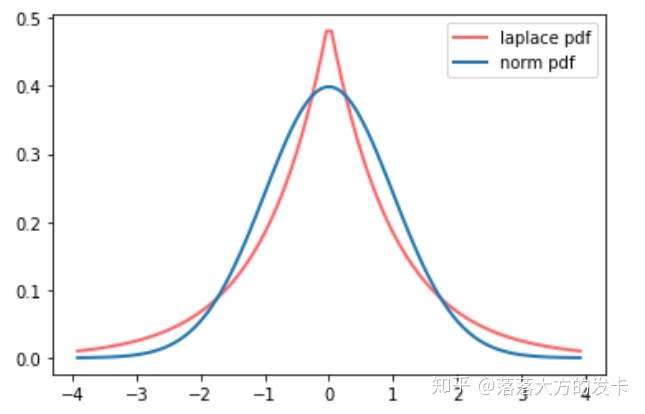
1.1 L1 正则化 【零均值拉普拉斯分布】
LASSO 回归, 相当于为模型添加了这样一个先验知识: \(\mathbf{w}\) 服从零均值拉普拉斯分布。首先看看拉普拉斯分布长什 么样子: \[ f(w \mid \mu, b)=\frac{1}{2 b} \exp \left(-\frac{|w-\mu|}{b}\right) \] 由于引入了先验知识, 所以似然函数这样写: \[ \begin{aligned} L(w) & =P(y \mid w, x) P(w) \\ & =\prod_{i=1}^N p\left(x_i\right)^{y_i}\left(1-p\left(x_i\right)\right)^{1-y_i} \prod_{j=1}^d \frac{1}{2 b} \exp \left(-\frac{\left|w_j\right|}{b}\right) \end{aligned} \] 取 \(\log\) 再取负,得到目标函数: \[ -\ln L(w)=-\sum_i\left[y_i \ln p\left(x_i\right)+\left(1-y_i\right) \ln \left(1-p\left(x_i\right)\right)\right]+\frac{1}{2 b^2} \sum_j\left|w_j\right| \] 等价于原始损失函数的后面加上了 L1 正则, 因此 L1 正则的本质其实是为模型增加了“模型参数服从零均值拉普拉 斯分布"这一先验知识。
1.2 L2 正则化【零均值正态分布】
Ridge 回归, 相当于为模型添加了这样一个先验知识: \(w\) 服从零均值正态分布。 首先看看正态分布长什么样子: \[ f(w \mid \mu, \sigma)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(w-\mu)^2}{2 \sigma^2}\right) \] 由于引入了先验知识, 所以似然函数这样写: \[ \begin{aligned} L(w) & =P(y \mid w, x) P(w) \\ & =\prod_{i=1}^N p\left(x_i\right)^{y_i}\left(1-p\left(x_i\right)\right)^{1-y_i} \prod_{j=1}^d \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{w_j^2}{2 \sigma^2}\right) \\ & =\prod_{i=1}^N p\left(x_i\right)^{y_i}\left(1-p\left(x_i\right)\right)^{1-y_i} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{w^T w}{2 \sigma^2}\right) \end{aligned} \] 取 In 再取负,得到目标函数: \[ -\ln L(w)=-\sum_i\left[y_i \ln p\left(x_i\right)+\left(1-y_i\right) \ln \left(1-p\left(x_i\right)\right)\right]+\frac{1}{2 \sigma^2} w^T w \] 等价于原始的损失函数后面加上了 \(L 2\) 正则, 因此 \(L 2\) 正则的本质其实是为模型增加了““模型参数服从零均值正态分 布"这一先验知识。
1.3 L1 和 L2 的区别
- 解空间约束条件 : KKT条件【互斥松弛条件 + 约束条件大于0】
- 函数叠加:(0点成为最值的可能)导数为0的可能性
- 贝叶斯先验:分布图像
L1 正则化增加了所有权重 w 参数的绝对值之和逼迫更多 w 为零,也就是变稀疏( L2 因为其导数也趋 0, 奔向零的速度不如 L1 给力了)。对稀疏规则趋之若鹜的一个关键原因在于它能实现特征的自动选择。L1 正则化的引入就是为了完成特征自动选择的光荣使命,它会学习地去掉这些无用的特征,也就是把这些特征对应的权重置为 0。
L2 正则化中增加所有权重 w 参数的平方之和,逼迫所有 w 尽可能趋向零但不为零(L2 的导数趋于零)。因为在未加入 L2 正则化发生过拟合时,拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大,在某些很小的区间里,函数值的变化很剧烈,也就是某些 w 值非常大。为此,L2 正则化的加入就惩罚了权重变大的趋势。
1.4 L1正则化使得模型参数具有稀疏性的原理?
(1) 解空间约束条件 : KKT条件【互斥松弛条件 + 约束条件大于0】
KKT 条件是指优化问题在最优处(包括基本型的最优值,对偶问题的最优值)必须满足的条件。
参考线性支持向量机的 KKT 条件:
- 主问题可行: \(g_{i}\left(u^{\star}\right)=1-y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right) \leq 0\) ;
- 对偶问题可行: \(\alpha_{i}^{\star} \geq 0\);
- 主变量最优: \(w^{\star}=\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}, \sum_{i=1}^{m} \alpha_{i} y_{i}=0\);
- 互补松弛: \(\alpha_{i}^{\star} g_{i}\left(u^{\star}\right)=\alpha_{i}^{\star}\left(1-y_{i}\left(w^{\star \top} x_{i}+b^{\star}\right)\right)=0\) ;
原函数曲线等高线(同颜色曲线上,每一组\(w_1,w_2\)带入后值都相同):
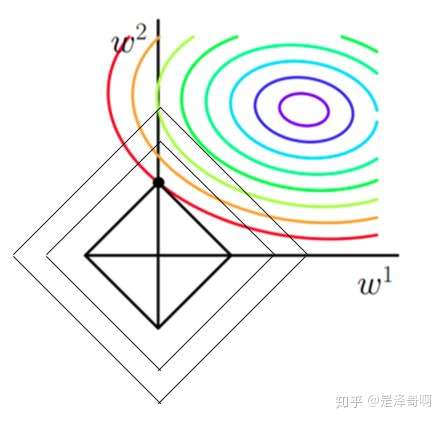
当加入 L1 正则化的时候, 我们先画出 \(\left|w_1\right|+\left|w_2\right|=F\) 的图像, 也就是一个菱形, 代表这些曲线上的点算出来的 要使得这个菱形越小越好 ( \(F\) 越小越好)。那么还和原来一样的话, 过中心紫色圈圈的那个菱形明显很大, 因此我 们要取到一个恰好的值。那么如何求值呢?
- 以同一条原曲线目标等高线来说, 现在以最外圈的红色等高线为例, 我们看到, 对于红色曲线上的每个点都可 做一个菱形, 根据上图可知, 当这个菱形与某条等高线相切(仅有一个交点)的时候, 这个菱形最小, 上图相 割对比较大的两个菱形对应的 L1 范数更大。用公式说这个时候能使得在相同的 \(\frac{1}{N} \sum_{i=1}^N\left(y_i-w^T x_i\right)^2\), 由于 相切的时候的 \(C|| w \|_1\) 小, 即 \(\left|w_1\right|+\left|w_2\right|\) 所以能够使得 \(\frac{1}{N} \sum i=1^N\left(y_i-w^T x_i\right)^2+C|| w \|_1\) 更小;
- 有了第一条的说明我们可以看出, 最终加入 \(L 1\) 范数得到的解一定是某个菱形和某条原函数等高线的切点。现 在有个比较重要的结论来了, 我们经过观察可以看到, 几乎对于很多原函数等高曲线, 和某个菱形相交的时 候及其容易相交在坐标轴 (比如上图) , 也就是说最终的结果, 解的某些维度及其容易是 0, 比如上图最终解 是 \(w=(0, x)\) ,这也就是我们所说的 L1 更容易得到稀疏解(解向量中 0 比较多)的原因;
- 当加入 \(L 2\) 正则化的时候, 分析和 \(L 1\) 正则化是类似的, 也就是说我们仅仅是从菱形变成了圆形而已, 同样还 是求原曲线和圆形的切点作为最终解。当然与 \(L 1\) 范数比, 我们这样求的 \(L 2\) 范数的从图上来看, 不容易交在 坐标轴上, 但是仍然比较靠近坐标轴。因此这也就是我们老说的, L2 范数能让解比较小 (靠近 0), 但是比 较平滑(不等于 0)。
(2) 函数叠加:(0点成为最值的可能)导数为0的可能性
我们接下来从更严谨的方式来证明, 简而言之就是假设现在我们是一维的情况下 \(h(w)=f(w)+C|w|\), 其中 \(h(w)\) 是目标函数, \(f(w)\) 是没加 \(\mathrm{L} 1\) 正则化项前的目标函数, \(C|w|\) 是 \(\mathrm{L}\) 正则项, 要使得 0 点成为最值可能的点, 虽然在 0 点不可导, 但是我们只需要让 0 点左右的导数异号, 即 \(h_l^{\prime}(0) h_r^{\prime}(0)=\left(f^{\prime}(0)+C\right)\left(f^{\prime}(0)-C\right)<0\) 即可也就 是 \(C>\left|f^{\prime}(0)\right|\) 的情况下, 0 点都是可能的最值点。相反, L2正则项在原点处的导数是0, 只要原目标函数在原点 处导数不为 0 , 那么最小值点就不会在原点, 所以 \(L 2\) 只有减小w最对值的作用, 对解空间的稀疏性没有贡献。
(3) 贝叶斯先验:分布图像

从贝叶斯加入先验分布的角度解释,L1正则化相当于对模型参数引入拉普拉斯先验,L2正则化相当于与引入了高斯先验。高斯分布在0点是平滑的,拉普拉斯在0点处是一个尖峰。
1.5 简单总结
| 正则化 | L1 正则化 | L2 正则化 |
|---|---|---|
| 服从分布 | 零均值拉普拉斯分布 | 零均值正态分布 |
| 损失函数变化 | \(\frac{1}{2 b^2} \sum_j\left |w_j\right|\) | \(\frac{1}{2 \sigma^2} w^T w\) |
| 模型参数w效果 | 逼迫更多 w 为零,【稀疏解】 (解空间约束条件、函数叠加、贝叶斯先验) | 趋向零但不为零【平滑】 |
| 作用 | 【特征选择】【降低模型复杂度】 | 【降低模型复杂度】 |