算法长征（13）结构设计

发表于 更新于 分类于 ， 阅读次数： 本文字数： 9k 阅读时长 ≈ 16 分钟

一、前缀树

一种好用的树结构：Trie树:https://zhuanlan.zhihu.com/p/508575094

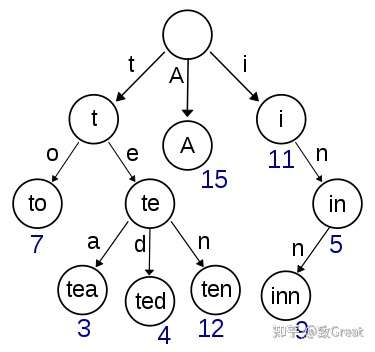
1.1 Trie树简介 [有限状态自动机] [文本词频统计]

在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

Trie这个术语来自于retrieval。根据词源学，trie的发明者Edward Fredkin把它读作/ˈtriː/ "tree"。但是，其他作者把它读作/ˈtraɪ/ "try"。

在图示中，键标注在节点中，值标注在节点之下。每一个完整的英文单词对应一个特定的整数。Trie可以看作是一个确定有限状态自动机，尽管边上的符号一般是隐含在分支的顺序中的。 Eg.一个保存了8个单词的字典树的结构如下图所示，8个单词分别是：“A”，“to”，“tea”，“ted”，“ten”，“i” ，“in”，“inn”。

img

另外，单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

1.2 Trie树性质

它有3个基本性质：

  • 根节点不包含字符，除根节点外每一个节点都只包含一个字符；
  • 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；
  • 每个节点的所有子节点包含的字符都不相同。

1.3 基本操作

其基本操作有：查找、插入和删除,当然删除操作比较少见。

1.4 实现方法

搜索字典项目的方法为：

  • 从根结点开始一次搜索；
  • 取得要查找关键词的第一个字母，并根据该字母选择对应的子树并转到该子树继续进行检索；
  • 在相应的子树上，取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
  • 迭代过程……
  • 在某个结点处，关键词的所有字母已被取出，则读取附在该结点上的信息，即完成查找。 其他操作类似处理

1.5 实现Trie (前缀树)

Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

  • Trie() :初始化前缀树对象。
    • self.children = [None] * 26 , 指向子节点的指针数组 children
    • self.isEnd = False , 表示该节点是否为字符串的结尾。
  • void insert(String word) :向前缀树中插入字符串 word 。
    • 我们从字典树的根开始，插入字符串。对于当前字符对应的子节点，有两种情况：
      • 子节点存在。沿着指针移动到子节点，继续处理下一个字符。
      • 子节点不存在。创建一个新的子节点，记录在children 数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符。
    • 重复以上步骤，直到处理字符串的最后一个字符，然后将当前节点标记为字符串的结尾。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
    • 我们从字典树的根开始，查找前缀。对于当前字符对应的子节点，有两种情况：
      • 子节点存在。沿着指针移动到子节点，继续搜索下一个字符。
      • 子节点不存在。说明字典树中不包含该前缀，返回空指针。
    • 重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Trie:
    def __init__(self):
        self.children = [None] * 26
        self.isEnd = False
    
    def searchPrefix(self, prefix: str) -> "Trie":
        node = self # 根节点
        for ch in prefix:
            ch = ord(ch) - ord("a")
            if not node.children[ch]:
                return None
            node = node.children[ch]
        return node

    def insert(self, word: str) -> None:
        node = self
        for ch in word:
            ch = ord(ch) - ord("a")
            if not node.children[ch]:
                node.children[ch] = Trie()
            node = node.children[ch]
        node.isEnd = True

    def search(self, word: str) -> bool:
        node = self.searchPrefix(word)
        return node is not None and node.isEnd

    def startsWith(self, prefix: str) -> bool:
        return self.searchPrefix(prefix) is not None

二、LRU

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class DLinkedNode:
    def __init__(self, key = 0, value = 0):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None
        
class LRUCache:
    def __init__(self, capacity: int):
      	# 使用伪头部和伪尾部节点    
        self.cache = dict()
        self.head = DLinkedNode()
        self.tail = DLinkedNode()
        self.head.next = self.tail
        self.tail.prev = self.head
        self.capacity = capacity
        self.size = 0

    def get(self, key: int) -> int:
        if key not in self.cache:
            return -1
        # 如果 key 存在，先通过哈希表定位，再移到头部
        node = self.cache[key]
        self.moveToHead(node)# "如果数据被访问过。那未来的访问几率更高"
        return node.value

    def put(self, key: int, value: int) -> None:
        if key not in self.cache:
          	# 如果 key 不存在，创建一个新的节点
            node = DLinkedNode(key, value)
            # 添加进哈希表
            self.cache[key] = node
            # 添加至双向链表的头部
            self.size += 1
            self.addToHead(node)
            if self.size > self.capacity:
              	# 如果超出容量，删除双向链表的尾部节点
                removed = self.removeTail()
                # 删除哈希表中对应的项
                self.cache.pop(removed.key)
                self.size -= 1
        else:
          	# 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node = self.cache[key]
            node.value = value
            self.moveToHead(node)

    def addToHead(self, node):
        node.prev = self.head
        node.next = self.head.next
        self.head.next.prev = node
        self.head.next = node
    
    def removeNode(self, node): 
        node.prev.next = node.next
        node.next.prev = node.prev

    def moveToHead(self, node):
        self.removeNode(node)
        self.addToHead(node)

    def removeTail(self):
        node = self.tail.prev
        self.removeNode(node)
        return node

LFU，最近不经常使用，把数据加入到链表中，按频次排序，一个数据被访问过，把它的频次+1，发生淘汰的时候，把频次低的淘汰掉。 比如有数据 1，1，1，2，2，3 缓存中有（1(3次)，2(2次)） 当3加入的时候，得把后面的2淘汰，变成（1(3次)，3(1次)） 区别：LRU 是得把 1 淘汰。

三、并查集

如果交换字符串 X 中的两个不同位置的字母，使得它和字符串 Y 相等，那么称 X 和 Y 两个字符串相似。如果这两个字符串本身是相等的，那它们也是相似的。例如，"tars" 和 "rats" 是相似的 (交换 0 与 2 的位置)； "rats" 和 "arts" 也是相似的，但是 "star" 不与 "tars"，"rats"，或 "arts" 相似。

总之，它们通过相似性形成了两个关联组：{"tars", "rats", "arts"} 和 {"star"}。注意，"tars" 和 "arts" 是在同一组中，即使它们并不相似。形式上，对每个组而言，要确定一个单词在组中，只需要这个词和该组中至少一个单词相似。

给定一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个 字母异位词 。请问 strs 中有多少个相似字符串组？

字母异位词（anagram），一种把某个字符串的字母的位置（顺序）加以改换所形成的新词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class UnionFind:
  	# 并查集
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.count = n
    def find(self, x):
        if self.parent[x] == x:
            return x
        self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    def union(self, x, y):
        x, y = self.find(x), self.find(y)
        if x != y:
            self.parent[x] = y
            self.count -= 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def numSimilarGroups(self, strs: List[str]) -> int:
      	# 相似的字符串
        m, n = len(strs), len(strs[0])
        un = UnionFind(m)
        for i in range(m):
            for j in range(i + 1, m):
                cnt = 0
                for k in range(n):
                    if strs[i][k] != strs[j][k]:
                        cnt += 1
                        if cnt > 2:
                            break
                else: # 上下文管理器
                    un.union(i, j)
        return un.count

四、序列化与反序列化

  • https://zhuanlan.zhihu.com/p/40462507

序列化：把对象转化为可传输的字节序列过程称为序列化。

反序列化：把字节序列还原为对象的过程称为反序列化。

4.1 序列化的定义

序列化：把对象转化为可传输的字节序列过程称为序列化。

反序列化：把字节序列还原为对象的过程称为反序列化。

4.2 为什么要序列化？

其实序列化最终的目的是为了对象可以跨平台存储，和进行网络传输。而我们进行跨平台存储和网络传输的方式就是IO，而我们的IO支持的数据格式就是字节数组。序列化只是一种拆装组装对象的规则，那么这种规则肯定也可能有多种多样，比如现在常见的序列化方式有：

JDK（不支持跨语言）、JSON、XML、Hessian、Kryo（不支持跨语言）、Thrift、Protostuff、FST（不支持跨语言）

请实现两个函数，分别用来序列化和反序列化二叉树。你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

  • 深度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Codec:
    def serialize(self, root):
        # 后续遍历 比 前序遍历快很多 pop(), pop(0)
        """ DFS : ncodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return 'None'
        return  str(self.serialize(root.left)) + ',' + str(self.serialize(root.right)) + ',' + str(root.val) 

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """
        def dfs(dfslist:list()):
            val = dfslist.pop()
            if val == 'None':
                return None
            root = TreeNode(int(val))
            root.right = dfs(dfslist)
            root.left = dfs(dfslist)
            return root
        dfslist = data.split(',')
        return dfs(dfslist)

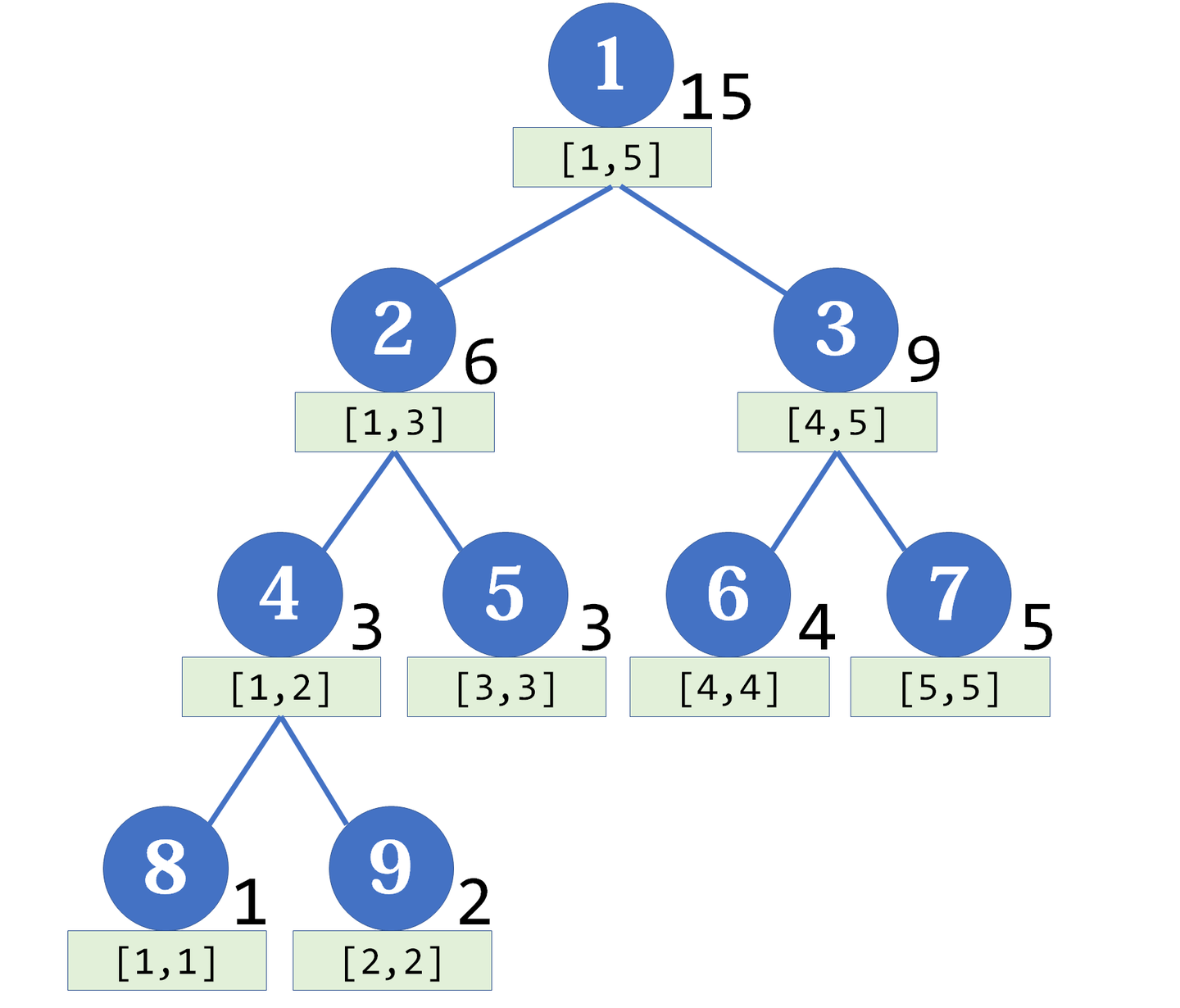
五、线段树

  • 算法学习笔记(14): 线段树：https://zhuanlan.zhihu.com/p/106118909

线段树（Segment Tree）几乎是算法竞赛最常用的数据结构了，它主要用于维护区间信息（要求满足结合律）。与树状数组相比，它可以实现 [公式] 的区间修改，还可以同时支持多种操作（加、乘)，更具通用性。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class BIT:
    # 线段树: 动态维护前缀和数据的结构
    def __init__(self, n):
        self.n = n
        self.tree = [0] * (n+1)
    @staticmethod
    def lowbit(x):
        # 二进制最小位1的位置
        return x&(-x)
    def query(self, x):
        ans = 0
        while x>0:
            ans += self.tree[x]
            x -= BIT.lowbit(x)
        return ans
    def update(self, x):
        while x<=self.n:
            self.tree[x] += 1
            x += BIT.lowbit(x)

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

  • 离散化树状数组

    • 单点更新 update(i, v)： 把序列 ii 位置的数加上一个值 v，这题 v=1
    • 区间查询 query(i)： 查询序列 [1⋯i] 区间的区间和，即 ii 位置的前缀和

修改和查询的时间代价都是 O(logn)，其中 n为需要维护前缀和的序列的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        # 离散化+线性数组 nums = [7,5,6,4]
        n = len(nums)
        # 求每个数比他小的有几个
        tmp = sorted(nums)
        for i in range(n):
            nums[i] = bisect.bisect_left(tmp, nums[i]) + 1
        # nums = [4,2,3,1]
        bit = BIT(n) # [0,0,0,0,0]
        ans = 0
        for i in range(n-1, -1, -1):
            ans += bit.query(nums[i] - 1)
            bit.update(nums[i])
        return ans

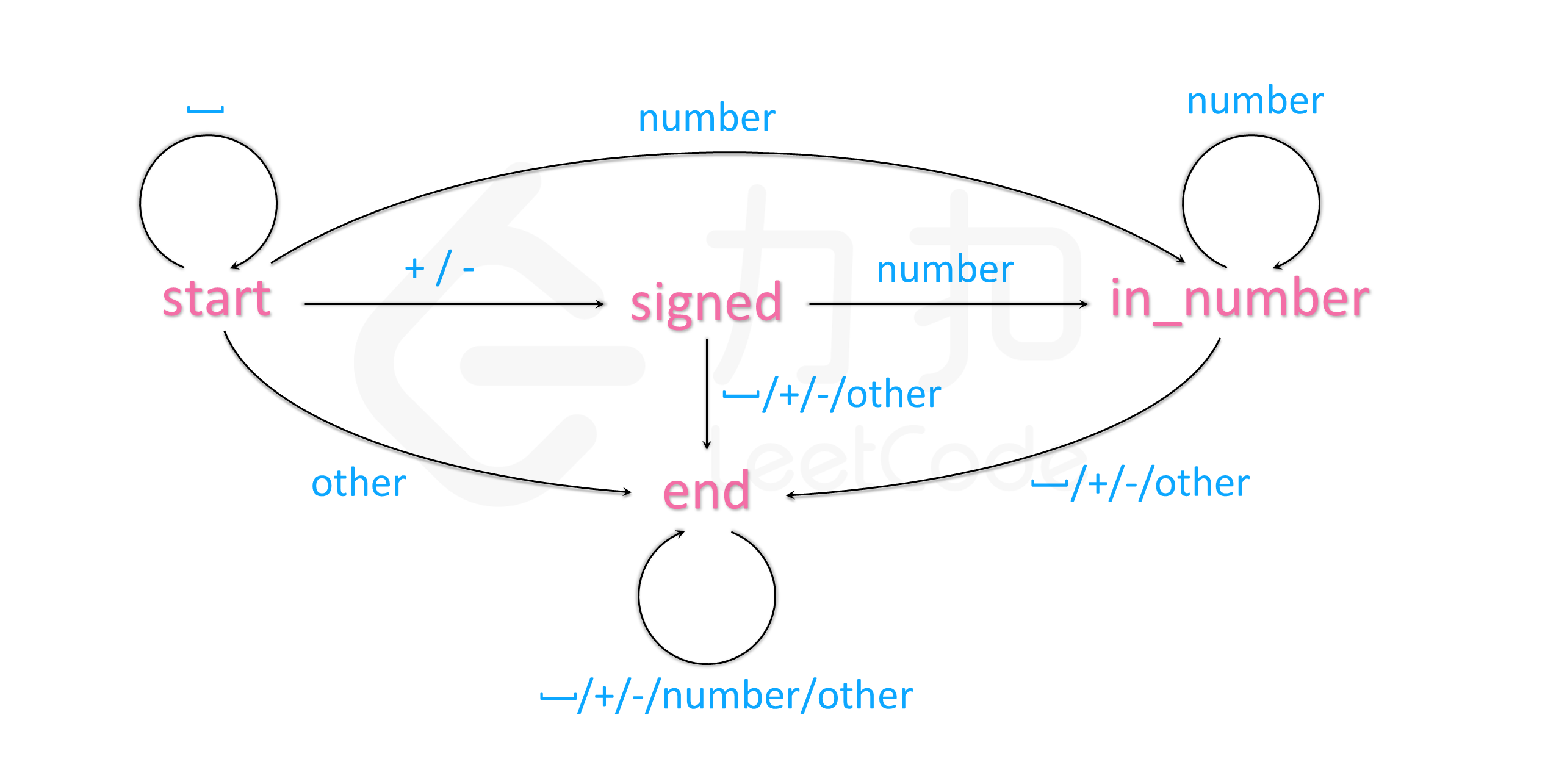
自动机

字符串处理的题目往往涉及复杂的流程以及条件情况，如果直接上手写程序，一不小心就会写出极其臃肿的代码。

因此，为了有条理地分析每个输入字符的处理方法，我们可以使用自动机这个概念：

我们的程序在每个时刻有一个状态 s，每次从序列中输入一个字符 c，并根据字符 c 转移到下一个状态 s'。这样，我们只需要建立一个覆盖所有情况的从 s 与 c 映射到 s' 的表格即可解决题目中的问题。

算法：

本题可以建立如下图所示的自动机：

fig1

我们也可以用下面的表格来表示这个自动机：

image-20220617125627816

接下来编程部分就非常简单了：我们只需要把上面这个状态转换表抄进代码即可。另外自动机也需要记录当前已经输入的数字，只要在 s' 为 in_number 时，更新我们输入的数字，即可最终得到输入的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
INT_MAX = 2 ** 31 - 1
INT_MIN = -2 ** 31

class Automaton:
    def __init__(self):
        self.state = 'start'
        self.sign = 1
        self.ans = 0
        self.table = {
            'start': ['start', 'signed', 'in_number', 'end'],
            'signed': ['end', 'end', 'in_number', 'end'],
            'in_number': ['end', 'end', 'in_number', 'end'],
            'end': ['end', 'end', 'end', 'end'],
        }
    def get_col(self, c):
        if c.isspace():
            return 0
        if c == '+' or c == '-':
            return 1
        if c.isdigit():
            return 2
        return 3

    def get(self, c):
        self.state = self.table[self.state][self.get_col(c)]
        if self.state == 'in_number':
            self.ans = self.ans * 10 + int(c)
            self.ans = min(self.ans, INT_MAX) if self.sign == 1 else min(self.ans, -INT_MIN)
        elif self.state == 'signed':
            self.sign = 1 if c == '+' else -1

class Solution:
    def myAtoi(self, str: str) -> int:
        automaton = Automaton()
        for c in str:
            automaton.get(c)
        return automaton.sign * automaton.ans