特征工程（3）特征选择

发表于 更新于 分类于 ， 阅读次数： 本文字数： 4.7k 阅读时长 ≈ 9 分钟

特征选择

【机器学习】特征选择(Feature Selection)方法汇总

特征选择方法全面总结

特征选择的基本方法总结

训练数据包含许多冗余或无用的特征，移除这些特征并不会导致丢失信息。其中冗余是指一个本身很有用的特征与另外一个有用的特征强相关，或它包含的信息能从其它特征推演出来; 特征很多但样本相对较少。

  • 产生过程：产生特征或特征子集候选集合；

  • 评价函数：衡量特征或特征子集的重要性或者好坏程度，即量化特征变量和目标变量之间的联系以及特征之间的相互联系。为了避免过拟合，可用交叉验证的方式来评估特征的好坏；

  • 停止准则：为了减少计算复杂度，需设定一个阈值，当评价函数值达到阈值后搜索停止

  • 验证过程：在验证数据集上验证选出来的特征子集的有效性

一、特征选择的目的

1.简化模型，使模型更易于理解：去除不相关的特征会降低学习任务的难度。并且可解释性能对模型效果的稳定性有更多的把握

2.改善性能：节省存储和计算开销

3.改善通用性、降低过拟合风险：减轻维数灾难，特征的增多会大大增加模型的搜索空间，大多数模型所需要的训练样本随着特征数量的增加而显著增加。特征的增加虽然能更好地拟合训练数据，但也可能增加方差

二、特征选择常见方法

  • Filter(过滤法)
    • 覆盖率
    • 方差选择
    • Pearson(皮尔森)相关系数
    • 卡方检验
    • 互信息法(KL散度、相对熵)和最大信息系数
    • Fisher得分
    • 相关特征选择
    • 最小冗余最大相关性
  • Wrapper(包装法)
    • 完全搜索
    • 启发搜索
    • 随机搜索
  • Embedded(嵌入法)
    • L1 正则项
    • 树模型选择
    • 不重要性特征选择

三、Filter(过滤法) 【特征集】

img
定义
  • 过滤法的思想就是不依赖模型，仅从特征的角度来做特征的筛选，具体又可以分为两种方法，一种是根据特征里面包含的信息量，如方差选择法，如果一列特征的方差很小，每个样本的取值都一样的话，说明这个特征的作用不大，可以直接剔除。另一种是对每一个特征，都计算关于目标特征的相关度，然后根据这个相关度来筛选特征，只保留高于某个阈值的特征，这里根据相关度的计算方式不同就可以衍生出一下很多种方法。
分类
  • 单变量过滤方法：不需要考虑特征之间的相互关系，按照特征变量和目标变量之间的相关性或互信息对特征进行排序，过滤掉最不相关的特征变量。优点是计算效率高、不易过拟合。
  • 多变量过滤方法：考虑特征之间的相互关系，常用方法有基于相关性和一致性的特征选择
覆盖率
  • 即特征在训练集中出现的比例。若覆盖率很小，如有10000个样本，但某个特征只出现了5次，则次覆盖率对模型的预测作用不大，可删除
（1）方差选择法
  • 先计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征
1
2
3
4
from sklearn.feature_selection import VarianceThreshold
# 方差选择法，返回值为特征选择后的数据
# 参数threshold为方差的阈值
VarianceThreshold(threshold=3).fit_transform(iris.data)
（2）Pearson皮尔森相关系数

用于度量两个变量X和Y之间的线性相关性

  • 用于度量两个变量X和Y之间的线性相关性，结果的取值区间为[-1, 1]， -1表示完全的负相关(这个变量下降，那个就会上升)，+1表示完全的正相关，0表示没有线性相关性
  • 计算方法为两个变量之间的协方差和标准差的商
1
2
3
4
5
6
7
8
9
from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr
  # 选择K个最好的特征，返回选择特征后的数据
  # 第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，
  # 输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。
  # 在此为计算相关系数
  # 其中参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, 
              k=2).fit_transform(iris.data, iris.target)
（3）卡方检验

自变量对因变量的相关性

检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量: \[ \chi^2=\sum \frac{(A-E)^2}{E} \]

1
2
3
4
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#选择K个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
（4）PSI互信息法(KL散度、相对熵)和最大信息系数 Mutual information and maximal information coefficient (MIC)

风控模型—群体稳定性指标(PSI)深入理解应用:https://zhuanlan.zhihu.com/p/79682292

评价定性自变量对定性因变量的相关性，评价类别型变量对类别型变量的相关性，互信息越大表明两个变量相关性越高，互信息为0时，两个变量相互独立。互信息的计算公式为 \[ I(X ; Y)=\sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)}=D_{K L}(p(x, y) \| p(x) p(y)) \]

（5）Fisher得分

对于分类问题, 好的特征应该是在同一个类别中的取值比较相似, 而在不同类别之间的取值差异比较大。因此特征 \(\mathrm{i}\) 的重要性可用Fiser得分 \(S_i\) 来表示 \[ S_i=\frac{\sum_{j=1}^K n_j\left(\mu_{i j}-\mu_i\right)^2}{\sum_{j=1}^K n_j \rho_{i j}^2} \] 其中, \(u_{i j}\) 和 \(\rho_{i j}\) 分别是特征i在类别 \(j\) 中均值和方差, \(\mu_i\) 为特征i的均值, \(n_j\) 为类别中中的样本数。Fisher得分越高, 特征在不同类别之间的差异性越大、在同一类别中的差异性越小，则特征越重要;

（6）相关特征选择

该方法基于的假设是，好的特征集合包含跟目标变量非常相关的特征，但这些特征之间彼此不相关

（7）最小冗余最大相关性( mRMR)

由于单变量过滤法只考虑了单特征变量和目标变量之间的相关性，因此选择的特征子集可能过于冗余。mRMR在进行特征时考虑到了特征之间的冗余性，具体做法是对跟已选择特征相关性较高的冗余特征进行惩罚;

四、Wrapper(包装法) 【特征集+模型】

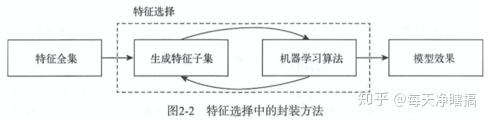
定义

  • 使用机器学习算法评估特征子集的效果，可以检测两个或多个特征之间的交互关系，而且选择的特征子集让模型的效果达到最优。

  • 这是特征子集搜索和评估指标相结合的方法。前者提供候选的新特征子集，后者基于新特征子集训练一个模型，并用验证集进行评估，为每一组特征子集进行打分。

  • 最简单的方法是在每一个特征子集上训练并评估模型，从而找出最优的特征子集

缺点：

  • 需要对每一组特征子集训练一个模型，计算量很大
  • 样本不够充分的情况下容易过拟合
  • 特征变量较多时计算复杂度太高
（1）完全搜索

即穷举法, 遍历所有可能的组合达到全局最优, 时间复杂度 \(2^n\)

（2）启发式搜索

序列向前选择: 特征子集从空集开始, 每次只加入一个特征, 时间复杂度为 \(O(n+(n-1)+(n-2)+\ldots+1)=O\left(n^2\right)\)

序列向后选择: 特征子集从全集开始, 每次删除一个特征, 时间复杂度为 \(O\left(n^2\right)\)

（3）随机搜索

执行序列向前或向后选择时，随机选择特征子集

（4）递归特征消除法

使用一个基模型进行多轮训练，每轮训练后通过学习器返回的coef_或者feature_importances_消除若干权重较低的特征，再基于新的特征集进行下一轮训练。

1
2
3
4
5
6
7
8
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), 
    n_features_to_select=2).fit_transform(iris.data, 
                                          iris.target)

五、Embedded（嵌入法）

将特征选择嵌入到模型的构建过程中，具有包装法与机器学习算法相结合的优点，也具有过滤法计算效率高的优点

（1）LASSO方法 L1正则项

通过对回归系数添加惩罚项来防止过拟合，可以让特定的回归系数变为0，从而可以选择一个不包含那些系数的更简单的模型；实际上，L1惩罚项降维的原理是，在多个对实际上，L1惩罚项降维的原理是，在多个对目标值具有同等相关性的特征中，只保留一个，所以没保留的特征并不代表不重要具有同等相关性的特征中，只保留一个，所以没保留的特征并不代表不重要。

1
2
3
4
5
6
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(LogisticRegression(
          penalty="l1", C=0.1)).fit_transform(
               iris.data,iris.target)
（2）基于树模型的特征选择方法
  • 在决策树中，深度较浅的节点一般对应的特征分类能力更强(可以将更多的样本区分开)
  • 对于基于决策树的算法，如随机森林，重要的特征更有可能出现在深度较浅的节点，而且出现的次数可能越多
  • 即可基于树模型中特征出现次数等指标对特征进行重要性排序
1
2
3
4
5
6
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
#GBDT作为基模型的特征选择
SelectFromModel(
    GradientBoostingClassifier()).fit_transform(
      iris.data,iris.target)
（3）使用特征重要性来筛选特征的缺陷？
  • 特征重要性只能说明哪些特征在训练时起到作用了，并不能说明特征和目标变量之间一定存在依赖关系。举例来说，随机生成一大堆没用的特征，然后用这些特征来训练模型，一样可以得到特征重要性，但是这个特征重要性并不会全是0，这是完全没有意义的。
  • 特征重要性容易高估数值特征和基数高的类别特征的重要性。这个道理很简单，特征重要度是根据决策树分裂前后节点的不纯度的减少量（基尼系数或者MSE）来算的，那么对于数值特征或者基础高的类别特征，不纯度较少相对来说会比较多。
  • 特征重要度在选择特征时需要决定阈值，要保留多少特征、删去多少特征，这些需要人为决定，并且删掉这些特征后模型的效果也不一定会提升。
（4）Non importance 选择