Pytorch（13）正则化

发表于 2022-05-02 更新于 2022-06-11 分类于【draft】工程，开源工具， Pytorch框架阅读次数：本文字数： 5.4k 阅读时长 ≈ 10 分钟

[PyTorch 学习笔记] weight decay、 dropout和Normalization

这篇文章主要介绍了正则化与偏差-方差分解，以及 PyTorch 中的 L2 正则项--weight decay

一、Regularization -weight decay

Regularization 中文是正则化，可以理解为一种减少方差的策略。

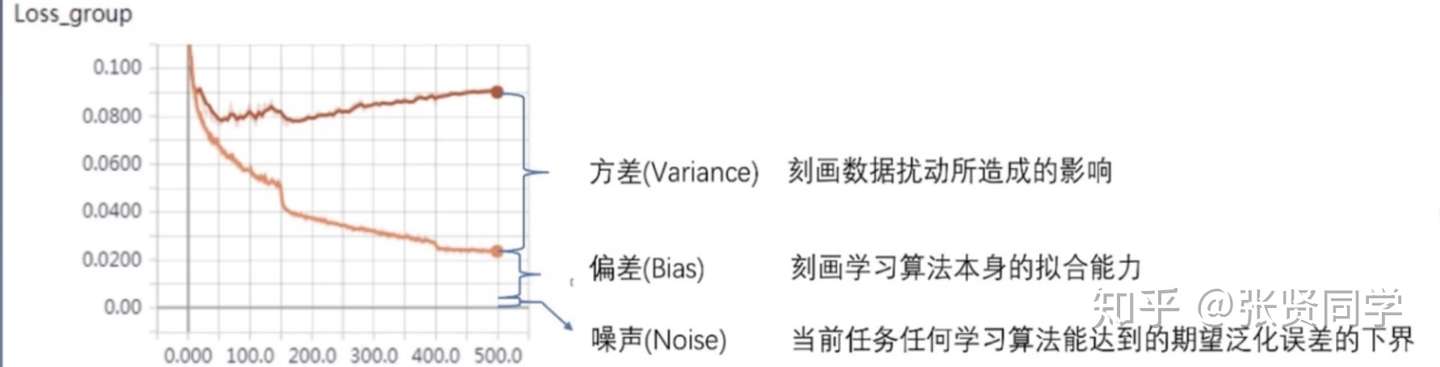
在机器学习中，误差可以分解为：偏差，方差与噪声之和。即误差=偏差+方差+噪声

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
噪声：表达了在当前任务上学习任何算法所能达到的期望泛化误差的下界。

正则化方式有 L1 和 L2 正则项两种。其中 L2 正则项又被称为权值衰减(weight decay)。

当没有正则项时： $\boldsymbol{O} \boldsymbol{b} \boldsymbol{j}=\boldsymbol{L} \boldsymbol{o} \boldsymbol{s} \boldsymbol{s}$ ， $w_{i+1}=w_{i}-\frac{\partial o b j}{\partial w_{i}}=w_{i}-\frac{\partial L o s s}{\partial w_{i}}$

当使用 L2 正则项时， $\boldsymbol{O} \boldsymbol{b} \boldsymbol{j}=\boldsymbol{L} \boldsymbol{o} \boldsymbol{s} \boldsymbol{s}+\frac{\lambda}{2} * \sum_{i}^{N} \boldsymbol{w}_{i}^{2}$ ， $\begin{aligned} w_{i+1}=w_{i}-\frac{\partial o b j}{\partial w_{i}} &=w_{i}-\left(\frac{\partial L o s s}{\partial w_{i}}+\lambda * w_{i}\right) =w_{i}(1-\lambda)-\frac{\partial L o s s}{\partial w_{i}} \end{aligned}$ ，其中 $0 < \lambda < 1$ ，所以具有权值衰减的作用。

二、Dropout

深度学习中Dropout原理解析 - Microstrong的文章 - 知乎 https://zhuanlan.zhihu.com/p/38200980

Dropout 是另一种抑制过拟合的方法。在使用 dropout 时，数据尺度会发生变化，如果设置 dropout_prob =0.3，那么在训练时，数据尺度会变为原来的 70%；==而在测试时，执行了 model.eval() 后，dropout 是关闭的，因此所有权重需要乘以 (1-dropout_prob)，把数据尺度也缩放到 70%==。加了 dropout 之后，权值更加集中在 0 附近，使得神经元之间的依赖性不至于过大。

PyTorch 中 Dropout 层如下，通常放在每个网路层的最前面：

1	torch.nn.Dropout(p=0.5, inplace=False)

参数：

p：主力需要注意的是，p 是被舍弃的概率，也叫失活概率；代码层面实现让某个神经元以概率p停止工作，其实就是让它的激活函数值以概率p变为0

2.1 Dropout具体工作流程

首先随机（临时）删掉网络中一部分的隐藏神经元，输入输出神经元保持不变（图3中虚线为部分临时被删除的神经元）
然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）。
恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
重复上述过程

2.2 ==为什么dropout 可以解决过拟合？== 【共享隐藏单元的bagging集成模型】

取平均的作用： 整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
Dropout纯粹作为一种高效近似Bagging的方法。然而,有比这更进一步的Dropout观点。==Dropout不仅仅是训练一个Bagging的集成模型,并且是共享隐藏单元的集成模型==。这意味着无论其他隐藏单元是否在模型中,每个隐藏单元必须都能够表现良好。

model.eval() 和 model.trian()

有些网络层在训练状态和测试状态是不一样的，如 dropout 层，在训练时 dropout 层是有效的，但是数据尺度会缩放，为了保持数据尺度不变，所有的权重需要除以 1-p。而在测试时 dropout 层是关闭的。因此在测试时需要先调用model.eval()设置各个网络层的的training属性为 False，在训练时需要先调用model.train()设置各个网络层的的training属性为 True。

三、Normalization

深度学习基础之 ---- BN、LN、IN、GN、SN - 琪小钧的文章 - 知乎 https://zhuanlan.zhihu.com/p/524829507

这篇文章主要介绍了 Batch Normalization 的概念，以及 PyTorch 中的 1d/2d/3d Batch Normalization 实现。

3.1 Batch Normalization

BN层的作用是把一个batch内的所有数据，从不规范的分布拉到正态分布。这样做的好处是使得数据能够分布在激活函数的敏感区域，敏感区域即为梯度较大的区域，因此在反向传播的时候能够较快反馈误差传播。

称为批标准化。批是指一批数据，通常为 mini-batch；经过处理后的数据符合均值为0，标准差为1的分布，如果原始的分布是正态分布，那么z-score标准化就将原始的正态分布转换为标准正态分布，机器学习中的很多问题都是基于正态分布的假设，这是更加常用的归一化方法。Batch Normalization 层一般在激活函数前一层。

批标准化的优点有如下：

可以使用更大的学习率，==加速模型收敛==
可以不用精心设计权值初始化
可以不用 dropout 或者较小的 dropout
可以不用 L2 或者较小的 weight decay
可以不用 LRN (local response normalization)

假设输入的 mini-batch 数据是 $\mathcal{B}=\left\{x_{1 \dots m}\right\}$ ，Batch Normalization 的可学习参数是 $\gamma, \beta$ ，步骤如下：

求 mini-batch 的均值： $\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i}$

求 mini-batch 的方差： $\sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}$

标准化： $\widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{B}^{2}+\epsilon}}$ ，其中 $\epsilon$ 是放置分母为 0 的一个数

affine transform(缩放和平移)： $y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{B} \mathrm{N}_{\gamma, \beta}\left(x_{i}\right)$ ，这个操作可以增强模型的 capacity，也就是让模型自己判断是否要对数据进行标准化，进行多大程度的标准化。如果 $\gamma= \sqrt{\sigma_{B}^{2}}$ ， $\beta=\mu_{\mathcal{B}}$ ，那么就实现了恒等映射。

Batch Normalization 的提出主要是为了解决 Internal Covariate Shift (ICS)。在训练过程中，数据需要经过多层的网络，如果数据在前向传播的过程中，尺度发生了变化，可能会导致梯度爆炸或者梯度消失，从而导致模型难以收敛。

带有 bn 层的 LeNet 定义如下：

class LeNet_bn(nn.Module):
    def __init__(self, classes):
        super(LeNet_bn, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.bn1 = nn.BatchNorm2d(num_features=6)

        self.conv2 = nn.Conv2d(6, 16, 5)
        self.bn2 = nn.BatchNorm2d(num_features=16)

        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.bn3 = nn.BatchNorm1d(num_features=120)

        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, classes)

    def forward(self, x):
        out = self.conv1(x)
        out = self.bn1(out)
        out = F.relu(out)

        out = F.max_pool2d(out, 2)

        out = self.conv2(out)
        out = self.bn2(out)
        out = F.relu(out)

        out = F.max_pool2d(out, 2)

        out = out.view(out.size(0), -1)

        out = self.fc1(out)
        out = self.bn3(out)
        out = F.relu(out)

        out = F.relu(self.fc2(out))
        out = self.fc3(out)
        return out

带 bn 层的网络，并且不使用 kaiming 初始化权值，训练过程如下：

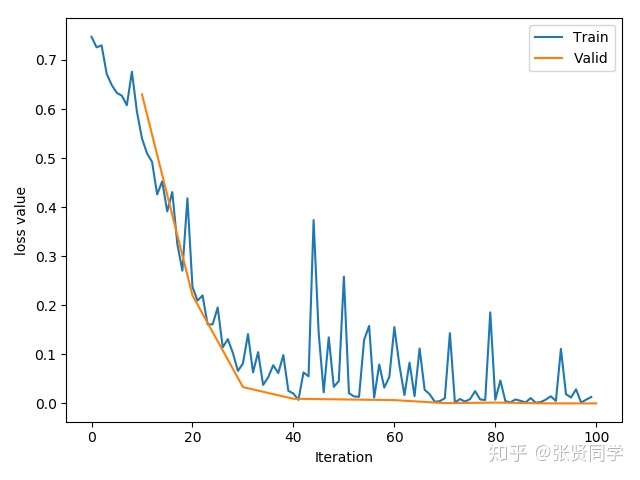
虽然训练过程中，训练集的 loss 也有激增，但只是增加到 0.4，非常稳定。

3.2 Batch Normalization in PyTorch

在 PyTorch 中，有 3 个 Batch Normalization 类

nn.BatchNorm1d()，输入数据的形状是 $B \times C \times 1D\_feature$
nn.BatchNorm2d()，输入数据的形状是 $B \times C \times 2D\_feature$
nn.BatchNorm3d()，输入数据的形状是 $B \times C \times 3D\_feature$

以nn.BatchNorm1d()为例，如下：

1	torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

参数：

num_features：一个样本的特征数量，这个参数最重要
eps：在进行标准化操作时的分布修正项
momentum：指数加权平均估计当前的均值和方差,在训练时，均值和方差采用指数加权平均计算，也就是不仅考虑当前 mini-batch 的值均值和方差还考虑前面的 mini-batch 的均值和方差。
affine：是否需要 affine transform，默认为 True
track_running_stats：True 为训练状态，此时均值和方差会根据每个 mini-batch 改变。False 为测试状态，此时均值和方差会固定

主要属性：

runninng_mean：均值
running_var：方差
weight：affine transform 中的 $\gamma$
bias：affine transform 中的 $\beta$

3.3 Layer Normalization

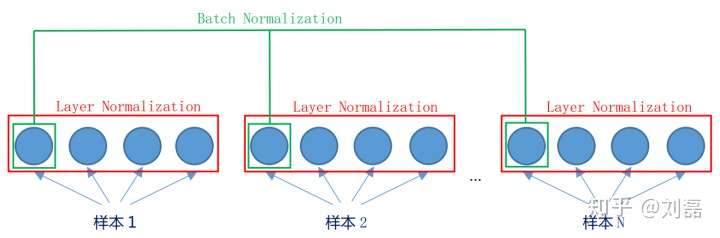
batch是“竖”着来的，各个维度做归一化，所以与batch size有关系。 layer是“横”着来的，对一个样本，不同的神经元neuron间做归一化。

提出的原因：Batch Normalization 不适用于变长的网络，如 RNN。如下显示了同一层的神经元的情况。假设这个mini-batch一共有N个样本，则Batch Normalization是对每一个维度进行归一。而Layer Normalization对于单个的样本就可以处理。bn和ln都可以比较好的抑制梯度消失和梯度爆炸的情况。思路：每个网络层计算均值和方差。

注意事项：

不再有 running_mean 和 running_var
$\gamma$ 和 $\beta$ 为逐样本的

1	torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

3.4 Instance Normalization

提出的原因：Batch Normalization 不适用于图像生成。因为在一个 mini-batch 中的图像有不同的风格，不能把这个 batch 里的数据都看作是同一类取标准化。

思路：逐个 instance 的 channel 计算均值和方差。也就是每个 feature map 计算一个均值和方差。

包括 InstanceNorm1d、InstanceNorm2d、InstanceNorm3d。

以InstanceNorm1d为例，定义如下：

1	torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)

参数：

num_features：一个样本的特征数，这个参数最重要
eps：分母修正项
momentum：指数加权平均估计当前的的均值和方差
affine：是否需要 affine transform
track_running_stats：True 为训练状态，此时均值和方差会根据每个 mini-batch 改变。False 为测试状态，此时均值和方差会固定

3.5 Group Normalization

提出的原因：在小 batch 的样本中，Batch Normalization 估计的值不准。一般用在很大的模型中，这时 batch size 就很小。

思路：数据不够，通道来凑。每个样本的特征分为几组，每组特征分别计算均值和方差。可以看作是 Layer Normalization 的基础上添加了特征分组。

4、相关问题

为啥用LN而不用BN在Transformer里？

BN是对一批数据进行归一化，一批里有不同的样本，bn对不同样本的同一个通道的特征（channel）进行均值方差操作；而LN对同一个样本内部的不同特征进行均值方差操作。

BN在batch size（N)和WH上进行缩放,保留C,而LN是在C和HW上进行缩放，保留bitch size,在NLP中就对应句子长度，通常来说文本词句的长度是不一样的，如果使用BN则会导致靠前的bitch size里的数据可以做相同的均值方差操作，而靠后的多余的数据的方差和均值难以估计，如下图

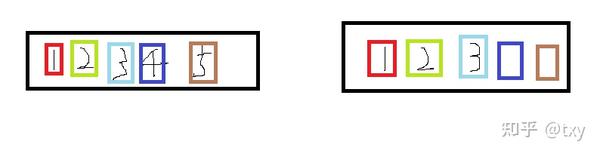
第一个样本里有5个数据通道（可看作特征），第二个样本空间里有3个数据通道（特征），则在提取特征时前三个的均值方差满足同一个norm操作公式，而后面两个由于第二个样本没有数据，所以均值方差不满足其公式，导致误差产生。