理论基础（5）模型评估

发表于 2022-03-24 更新于 2023-04-26 分类于算法，机器学习，理论基础阅读次数：本文字数： 3.7k 阅读时长 ≈ 7 分钟

一、A/B 测试

【AB测试最全干货】史上最全知识点及常见面试题（上篇） - 数据分析狗一枚的文章 - 知乎 https://zhuanlan.zhihu.com/p/375902281

引言

科学家门捷列夫说「没有测量，就没有科学」，在AI场景下我们同样需要定量的数值化指标来指导我们更好地应用模型对数据进行学习和建模。

事实上，在机器学习领域，对模型的测量和评估至关重要。选择与问题相匹配的评估方法，能帮助我们快速准确地发现在模型选择和训练过程中出现的问题，进而对模型进行优化和迭代。本文我们系统地讲解一下机器学习模型评估相关知识。

1.1 模型评估的目标

模型评估的目标是选出泛化能力强的模型完成机器学习任务。实际的机器学习任务往往需要进行大量的实验，经过反复调参、使用多种模型算法（甚至多模型融合策略）来完成自己的机器学习问题，并观察哪种模型算法在什么样的参数下能够最好地完成任务。

但是我们无法提前获取「未知的样本」，因此我们会基于已有的数据进行切分来完成模型训练和评估，借助于切分出的数据进行评估，可以很好地判定模型状态（过拟合 or 欠拟合），进而迭代优化。

在建模过程中，为了获得泛化能力强的模型，我们需要一整套方法及评价指标。

评估方法：为保证客观地评估模型，对数据集进行的有效划分实验方法。
性能指标：量化地度量模型效果的指标。

1.2 离线与在线实验方法

进行评估的实验方法可以分为「离线」和「在线」两种。

离线实验方法：

在离线评估中，经常使用准确率（Accuracy）、查准率（Precision）、召回率（Recall）、ROC、AUC、PRC等指标来评估模型。

模型评估通常指离线试验。原型设计（Prototyping）阶段及离线试验方法，包含以下几个过程：

使用历史数据训练一个适合解决目标任务的一个或多个机器学习模型。
对模型进行验证（Validation）与离线评估（Offline Evaluation）。
通过评估指标选择一个较好的模型。

在线实验方法：

在线评估与离线评估所用的评价指标不同，一般使用一些商业评价指标，如用户生命周期值（Customer Lifetime value）、广告点击率（Click Through Rate）、用户流失率（Customer Churn Rate）等标。

除了离线评估之外，其实还有一种在线评估的实验方法。由于模型是在老的模型产生的数据上学习和验证的，而线上的数据与之前是不同的，因此离线评估并不完全代表线上的模型结果。因此我们需要在线评估，来验证模型的有效性。

\(A/B Test\) 是目前在线测试中最主要的方法。 \(A/B Test\) 是为同一个目标制定两个方案让一部分用户使用 \(A\) 方案, 另一部分用户使用 \(B\) 方案, 记录下用户的使用情况, 看哪个方案更符合设计目标。如果不做AB实验直接上线新方案，新方案甚至可能会毁掉你的产品。

1.3 模型离线评估后，为什么要进行ab测试？

离线评估无法消除过拟合的影响，因此离线评估结果无法代替线上的评估效果
离线评估过程中无法模拟线上的真实环境，例如数据丢失、样本反馈延迟
线上的某些商业指标例如收益、留存等无法通过离线计算

1.4 如何进行线上ab测试？

进行ab测试的主要手段时对用户进行分桶，即将用户分成实验组和对照组。实验组使用新模型，对照组使用base模型。分桶过程中需要保证样本的独立性和采样的无偏性，确保每个用户只划分到一个桶中，分桶过程中需要保证user id是一个随机数，才能保证数据无偏的。

二、模型评估

2.1 holdout

留出法是机器学习中最常见的评估方法之一，它会从训练数据中保留出验证样本集，这部分数据不用于训练，而用于模型评估。

2.2 交叉验证

留出法的数据划分，可能会带来偏差。在机器学习中，另外一种比较常见的评估方法是交叉验证法—— \(K\) 折交叉验证对\(K\) 个不同分组训练的结果进行平均来减少方差。

2.3 自助法

Bootstrap 是一种用小样本估计总体值的一种非参数方法，在进化和生态学研究中应用十分广泛。Bootstrap通过有放回抽样生成大量的伪样本，通过对伪样本进行计算，获得统计量的分布，从而估计数据的整体分布。

三、超参数调优

神经网咯是有许多超参数决定的，例如网络深度，学习率，正则等等。如何寻找最好的超参数组合，是一个老人靠经验，新人靠运气的任务。

3.1 网格搜索

3.2 随机搜索

3.3 贝叶斯优化

贝叶斯优化什么?【黑盒优化】

求助 gradient-free 的优化算法了，这类算法也很多了，贝叶斯优化就属于无梯度优化算法中的一种，它希望在尽可能少的试验情况下去尽可能获得优化命题的全局最优解。

目标函数 \(f(x)\) 及其导数末知, 否则就可以用梯度下降等方法求解。
计算目标函数时间成本大, 意味着像蚁群算法、遗传算法这种方法也失效了, 因为计算一次要花费很多时间。

概述

贝叶斯优化, 是一种使用贝叶斯定理来指导搜索以找到目标函数的最小值或最大值的方法, 就是在每次迭代的时候, 利用之前观测到的历史信息 (先验知识) 来进行下一次优化, 通俗点讲, 就是在进行一次迭代的时候, 先回顾下之前的迭代结果, 结果太差的 \(x\) 附近就不去找了, 尽量往结果好一点的 \(x\) 附近去找最优解, 这样一来搜索的效率就大大提高了, 这其实和人的思维方式也有点像, 每次在学习中试错, 并且在下次的时候根据这些经验来找到最优的策略。

贝叶斯优化过程

首先，假设有一个这样的函数\(c(x)\)，我们需要找到他的最小值，如下图所示，这也是我们所需要优化的目标函数，但是我们并不能够知道他的具体形状以及表达形式是怎么样的。

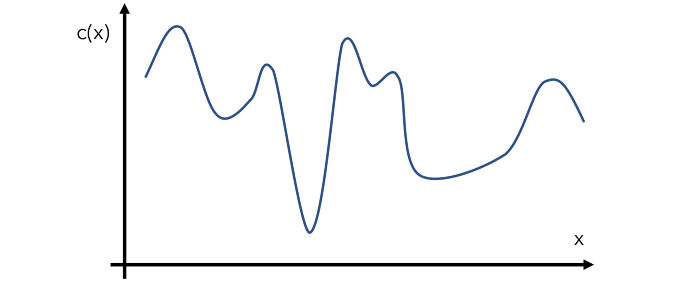
贝叶斯优化是通过一种叫做代理优化的方式来进行的，就是不知道真实的目标函数长什么样，我们就用一个代理函数（surrogate function）来代替目标函数，而这个代理函数就可以通过先采样几个点，再通过这几个点来给他拟合出来，如下图虚线所示：

基于构造的代理函数, 我们就可以在可能是最小值的点附近采集更多的点, 或者在还没有采样过的区域来采集更多的点，有了更多点，就可以更新代理函数，使之更逼近真实的目标函数的形状，这样的话也更容易找到目标函数的最小值, 这个采样的过程同样可以通过构建一个采集函数来表示, 也就是知道了当前代理函数的形状, 如何选择下一个 \(x\) 使得收益最大。

然后重复以上过程，最终就可以找到函数的最小值点了，这大致就是贝叶斯优化的一个过程:

初始化一个代理函数的先验分布
选择数据点 \(x\), 使得采集函数 \(a(x)\) 取最大值
在目标函数 \(c(x)\) 中评估数据点 \(x\) 并获取其结果 \(y\)
使用新数据 \((x, y)\) 更新代理函数，得到一个后验分布 (作为下一步的先验分布)
重复2-4步，直到达到最大迭代次数

举个例子, 如图所示, 一开始只有两个点 \((\mathrm{t}=2)\), 代理函数的分布是紫色的区域那块, 然后根据代理函数算出一个采集函数（绿色线), 取采集函数的最大值所在的 \(x\) (红色三角处), 算出 \(y\), 然后根据新的点 \((x, y)\) 更新代理函数和采集函数 \((\mathrm{t}=3)\) ，继续重复上面步骤，选择新的采集函数最大值所在的 \(x\), 算出 \(y\), 再更新代理函数和采集函数, 然后继续迭代。