降维（3）t-SNE

发表于 2022-03-16 更新于 2023-04-22 分类于算法，机器学习，降维与度量学习阅读次数：本文字数： 3.8k 阅读时长 ≈ 7 分钟

一、t-SNE 高维数据可视化

高维数据可视化之t-SNE算法🌈:https://zhuanlan.zhihu.com/p/57937096

T-SNE算法是用于可视化的算法中效果最好的算法之一，相信大家也对T-SNE算法略有耳闻，本文参考T-SNE作者Laurens van der Maaten给出的源代码自己实现T-SNE算法代码，以此来加深对T-SNE的理解。先简单介绍一下T-SNE算法，T-SNE将数据点变换映射到概率分布上。

1.1 t-SNE数据算法的目的

主要是将数据从高维数据转到低维数据，并在低维空间里也保持其在高维空间里所携带的信息（比如高维空间里有的清晰的分布特征，转到低维度时也依然存在）。

t-SNE将欧氏距离距离转换为条件概率，来表达点与点之间的相似度，再优化两个分布之间的距离-KL散度，从而保证点与点之间的分布概率不变。

1.2 SNE原理

\(S N E\) 是通过仿射变换将数据点映射到相应概率分布上, 主要包括下面两个步骤: 1. 通过在高维空间中构建数据点之间的概率分布 \(P\), 使得相似的数据点有更高的概率被选择, 而不相似的数据点有较低的概率被选择; 2. 然后在低维空间里重构这些点的概率分布 \(Q\), 使得这两个概率分布尽可能相似。

令输入空间是 \(X \in \mathbb{R}^{n}\), 输出空间为 \(Y \in \mathbb{R}^{t}(t \ll n)\) 。不妨假设含有 \(m\) 个样本数据 \(\left\{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right\}\), 其中 \(x^{(i)} \in X\), 降维后的数据为 \(\left\{y^{(1)}, y^{(2)}, \cdots, y^{(m)}\right\}, y^{(i)} \in Y\) 。 \(S N E\) 是先将欧几里得距离转化为条件概率来表达点与点之间的相似度, 即首先是计算条件概率 \(p_{j \mid i}\), 其正比于 \(x^{(i)}\) 和 \(x^{(j)}\) 之间的相似度, \(p_{j \mid i}\) 的计算公式为: \[ p_{j \mid i}=\frac{\exp \left(-\frac{\left\|x^{(i)}-x^{(j)}\right\|^{2}}{2 \sigma_{i}^{2}}\right)}{\sum_{k \neq i} \exp \left(-\frac{\left\|x^{(i)}-x^{(k)}\right\|^{2}}{2 \sigma_{i}^{2}}\right)} \] 在这里引入了一个参数 \(\sigma_{i}\), 对于不同的数据点 \(x^{(i)}\) 取值亦不相同, 因为我们关注的是不同数据点两两之间的相似度, 故可设置 \(p_{i \mid i}=0\) 。对于低维度下的数据点 \(y^{(i)}\), 通过条件概率 \(q_{j \mid i}\) 来刻画 \(y^{(i)}\) 与 \(y^{(j)}\) 之间的相似度, \(q_{j \mid i}\) 的计算公式为: \[ q_{j \mid i}=\frac{\exp \left(-\left\|y^{(i)}-y^{(j)}\right\|^{2}\right)}{\sum_{k \neq i} \exp \left(-\left\|y^{(i)}-y^{(k)}\right\|^{2}\right)} \] 同理, 设置 \(q_{i \mid i}=0\) 。如果降维的效果比较好, 局部特征保留完整, 那么有 \(p_{i \mid j}=q_{i \mid j}\) 成立, 因此通过优化两个分布之间的 \(K L\) 散度构造出的损失函数为: \[ C\left(y^{(i)}\right)=\sum_{i} K L\left(P_{i} \| Q_{i}\right)=\sum_{i} \sum_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}} \] 这里的 \(P_{i}\) 表示在给定高维数据点 \(x^{(i)}\) 时, 其他所有数据点的条件概率分布; \(Q_{i}\) 则表示在给定低维数据点 \(y^{(i)}\) 时, 其他所有数据点的条件概率分布。从损失函数可以看出, 当 \(p_{j \mid i}\) 较大 \(q_{j \mid i}\) 较小时, 惩罚较高; 而 \(p_{j \mid i}\) 较小 \(q_{j \mid i}\) 较大时, 惩罚较低。换句话说就是高维空间中两个数据点距离较近时, 若映射到低维空间后距离较远, 那么将得到一个很高的惩罚; 反之, 高维空间中两个数据点距离较远时, 若映射到低维空间距离较近, 将得到一个很低的惩罚值。也就是说, \(S N E\) 的损失函数更关注于局部特征, 而忽视了全局结构。

1.3 目标函数求解

1.4 对称性-SNE

优化 \(K L(P \| Q)\) 的一种替换思路是使用联合概率分布来替换条件概率分布, 即 \(P\) 是高维空间里数据点的联合概率分布, \(Q\) 是低维空间里数据点的联合概率分布，此时的损失函数为: \[ C\left(y^{(i)}\right)=K L(P \| Q)=\sum_i \sum_j p_{i j} \log \frac{p_{i j}}{q_{i j}} \] 同样的 \(p_{i i}=q_{i i}=0\) ，这种改进下的 \(S N E\) 称为对称 \(S N E\) ，因为它的先验假设为对 \(\forall i\) 有 \(p_{i j}=p_{j i}, q_{i j}=q_{j i}\) 成立，故概率分布可以改写成: \[ p_{i j}=\frac{\exp \left(-\frac{\left\|x^{(i)}-x^{(j)}\right\|^2}{2 \sigma^2}\right)}{\sum_{k \neq l} \exp \left(-\frac{\left\|x^{(k)}-x^{(l)}\right\|^2}{2 \sigma^2}\right)} \quad q_{i j}=\frac{\exp \left(-\left\|y^{(i)}-y^{(j)}\right\|^2\right)}{\sum_{k \neq l} \exp \left(-\left\|y^{(k)}-y^{(l)}\right\|^2\right)} \] 这种改进方法使得表达式简洁很多, 但是容易受到异常点数据的影响, 为了解决这个问题通过对联合概率分布定义修正为： \(p_{i j}=\frac{p_{j \mid i}+p_{i \mid j}}{2}\), 这保证了 \(\sum_j p_{i j}>\frac{1}{2 m}\) ，使得每个点对于损失函数都会有贡献。对称 \(S N E\) 最大的优点是简化了梯度计算, 梯度公式改写为: \[ \frac{\partial C\left(y^{(i)}\right)}{\partial y^{(i)}}=4 \sum_j\left(p_{i j}-q_{i j}\right)\left(y^{(i)}-y^{(j)}\right) \] 研究表明, 对称 \(S N E\) 和 \(S N E\) 的效果差不多, 有时甚至更好一点。

1.5 t-SNE

\(t-S N E\) 在对称 \(S N E\) 的改进是, 首先通过在高维空间中使用高斯分布将距离转换为概率分布，然后在低维空间中，使用更加偏重长尾分布的方式来将距离转换为概率分布，使得高维度空间中的中低等距离在映射后能够有一个较大的距离。

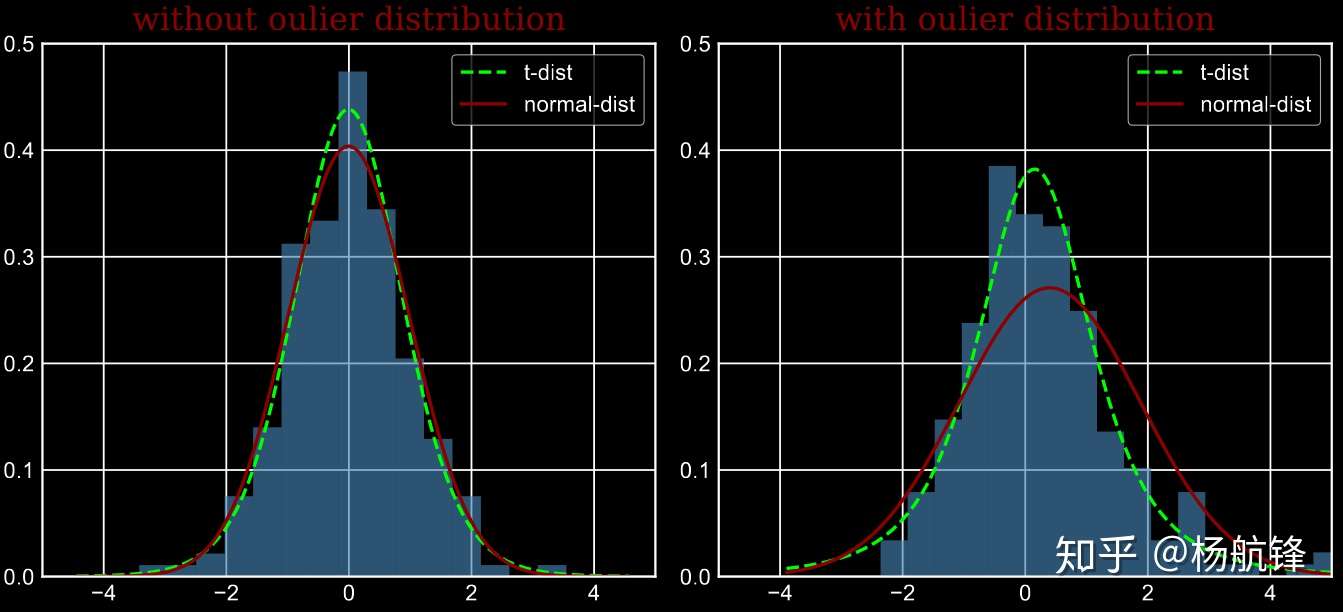
从图中可以看到，在没有异常点时, \(t\) 分布与高斯分布的拟合结果基本一致。而在第二张图中, 出现了部分异常点, 由于高斯分布的尾部较低, 对异常点比较敏感, 为了照顾这些异常点, 高斯分布的拟合结果偏离了大多数样本所在位置, 方差也较大。相比之下, \(t\) 分布的尾部较高, 对异常点不敏感, 保证了其鲁棒性, 因此拟合结果更为合理, 较好的捕获了数据的全局特征。

使用 \(t\) 分布替换高斯分布之后 \(q_{i j}\) 的变化如下: \[ q_{i j}=\frac{\left(1+\left\|y^{(i)}-y^{(j)}\right\|^2\right)^{-1}}{\sum_{k \neq l}\left(1+\left\|y^{(i)}-y^{(j)}\right\|^2\right)^{-1}} \] 此外，随着自由度的逐渐增大, \(t\) 分布的密度函数逐渐接近标准正态分布，因此在计算梯度方面会简单很多, 优化后的梯度公式如下: \[ \frac{\partial C\left(y^{(i)}\right)}{\partial y^{(i)}}=4 \sum_j\left(p_{i j}-q_{i j}\right)\left(y^{(i)}-y^{(j)}\right)\left(1+\left\|y^{(i)}-y^{(j)}\right\|^2\right)^{-1} \] 总的来说, \(t-S N E\) 的梯度更新具有以下两个优势： - 对于低维空间中不相似的数据点，用一个较小的距离会产生较大的梯度让这些数据点排斥开来; - 这种排斥又不会无限大，因此避免了不相似的数据点距离太远。

\(t-S N E\) 算法其实就是在 \(S N E\) 算法的基础上增加了两个改进:

把 \(S N E\) 修正为对称 \(S N E\) ，提高了计算效率, 效果稍有提升;
在低维空间中采用了 \(t\) 分布替换原来的高斯分布，解决了高维空间映射到低维空间所产生的拥挤问题, 优化了 \(S N E\) 过于关注局部特征而忽略全局特征的问题。