Pytorch（10）模型训练-损失函数

发表于 2022-05-02 更新于 2022-06-30 分类于【draft】工程，开源工具， Pytorch框架阅读次数：本文字数： 6.6k 阅读时长 ≈ 12 分钟

[PyTorch 学习笔记] 损失函数

一、损失函数

损失函数是衡量模型输出与真实标签之间的差异。我们还经常听到代价函数和目标函数，它们之间差异如下：

损失函数(Loss Function)是计算一个样本的模型输出与真实标签的差异 Loss $=f\left(y^{\wedge}, y\right)$
代价函数(Cost Function)是计算整个样本集的模型输出与真实标签的差异，是所有样本损失函数的平均值 $\cos t=\frac{1}{N} \sum_{i}^{N} f\left(y_{i}^{\wedge}, y_{i}\right)$
目标函数(Objective Function)就是代价函数加上正则项

在 PyTorch 中的损失函数也是继承于nn.Module，所以损失函数也可以看作网络层。

在逻辑回归的实验中，我使用了交叉熵损失函数loss_fn = nn.BCELoss()， $BCELoss$ 的继承关系：nn.BCELoss() -> _WeightedLoss -> _Loss -> Module。在计算具体的损失时loss = loss_fn(y_pred.squeeze(), train_y)，这里实际上在 Loss 中进行一次前向传播，最终调用BCELoss()的forward()函数F.binary_cross_entropy(input, target, weight=self.weight, reduction=self.reduction)。

1.1 nn.CrossEntropyLoss = softmax(x)+log(x)+nn.NLLLoss

1	nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

功能：把nn.LogSoftmax()和nn.NLLLoss()结合，计算交叉熵。nn.LogSoftmax()的作用是把输出值归一化到了 [0,1] 之间。

weight：各类别的 loss 设置权值
ignore_index：忽略某个类别的 loss 计算
reduction：计算模式，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

==下面介绍熵的一些基本概念==

自信息： $\mathrm{I}(x)=-\log [p(x)]$

信息熵就是求自信息的期望： $\mathrm{H}(\mathrm{P})=E_{x \sim p}[I(x)]=-\sum_{i}^{N} P\left(x_{i}\right) \log P\left(x_{i}\right)$

相对熵，也被称为 KL 散度，用于衡量两个分布的相似性(距离)： $\boldsymbol{D}_{K L}(\boldsymbol{P}, \boldsymbol{Q})=\boldsymbol{E}_{\boldsymbol{x} \sim p}\left[\log \frac{\boldsymbol{P}(\boldsymbol{x})}{Q(\boldsymbol{x})}\right]$ 。其中 $P(X)$ 是真实分布， $Q(X)$ 是拟合的分布

交叉熵： $\mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right)$

相对熵展开可得：

$\begin{aligned} \boldsymbol{D}_{K L}(\boldsymbol{P}, \boldsymbol{Q}) &=\boldsymbol{E}_{\boldsymbol{x} \sim p}\left[\log \frac{P(x)}{Q(\boldsymbol{x})}\right] \\ &=\boldsymbol{E}_{\boldsymbol{x} \sim p}[\log P(\boldsymbol{x})-\log Q(\boldsymbol{x})] \\ &=\sum_{i=1}^{N} P\left(x_{i}\right)\left[\log P\left(\boldsymbol{x}_{i}\right)-\log Q\left(\boldsymbol{x}_{i}\right)\right] \\ &=\sum_{i=1}^{N} P\left(\boldsymbol{x}_{i}\right) \log P\left(\boldsymbol{x}_{i}\right)-\sum_{i=1}^{N} P\left(\boldsymbol{x}_{i}\right) \log \boldsymbol{Q}\left(\boldsymbol{x}_{i}\right) \\ &= H(P,Q) -H(P) \end{aligned}$

所以交叉熵 = 信息熵 + 相对熵，即 $\mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=\boldsymbol{D}_{K \boldsymbol{L}}(\boldsymbol{P}, \boldsymbol{Q})+\mathrm{H}(\boldsymbol{P})$ ，又由于信息熵 $H(P)$ 是固定的，因此==优化交叉熵 $H(P,Q)$ 等价于优化相对熵== $D_{KL}(P,Q)$ 。

所以对于每一个样本的 Loss 计算公式为：

$\mathrm{H}(\boldsymbol{P}, \boldsymbol{Q})=-\sum_{i=1}^{N} \boldsymbol{P}\left(\boldsymbol{x}_{\boldsymbol{i}}\right) \log Q\left(\boldsymbol{x}_{\boldsymbol{i}}\right) = logQ(x_{i})$ ，因为 $N=1$ ， $P(x_{i})=1$ 。

所以 $\operatorname{loss}(x, \text { class })=-\log \left(\frac{\exp (x[\text { class }])}{\sum_{j} \exp (x[j])}\right)=-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right)$ 。

如果了类别的权重，则 $\operatorname{loss}(x, \text { class })=\operatorname{weight}[\text { class }]\left(-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right)\right)$ 。

下面设有 3 个样本做 2 分类。inputs 的形状为 $3 \times 2$ ，表示每个样本有两个神经元输出两个分类。target 的形状为 $3 \times 1$ ，注意类别从 0 开始，类型为torch.long。

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np

# fake data
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
target = torch.tensor([0, 1, 1], dtype=torch.long)

# def loss function
loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')

# forward
loss_none = loss_f_none(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print("Cross Entropy Loss:", loss_none, loss_sum, loss_mean)

输出为：

1	Cross Entropy Loss: tensor([1.3133, 0.1269, 0.1269]) tensor(1.5671) tensor(0.5224)

1.2 nn.NLLLoss

1	nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

功能：实现负对数似然函数中的符号功能

主要参数：

weight：各类别的 loss 权值设置
ignore_index：忽略某个类别
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

每个样本的 loss 公式为： $l_{n}=-w_{y_{n}} x_{n, y_{n}}$ 。还是使用上面的例子，第一个样本的输出为 [1,2]，类别为 0，则第一个样本的 loss 为 -1；第一个样本的输出为 [1,3]，类别为 1，则第一个样本的 loss 为 -3。

1.3 nn.BCELoss

1	nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

功能：计算二分类的交叉熵。需要注意的是：输出值区间为 [0,1]。

主要参数：

weight：各类别的 loss 权值设置
ignore_index：忽略某个类别
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

计算公式为： $l_{n}=-w_{n}\left[y_{n} \cdot \log x_{n}+\left(1-y_{n}\right) \cdot \log \left(1-x_{n}\right)\right]$

使用这个函数有两个不同的地方：

预测的标签需要经过 sigmoid 变换到 [0,1] 之间。
真实的标签需要转换为 one hot 向量，类型为torch.float。

1.4 nn.BCEWithLogitsLoss

1	nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)

功能：结合 sigmoid 与二分类交叉熵。需要注意的是，网络最后的输出不用经过 sigmoid 函数。这个 loss 出现的原因是有时网络模型最后一层输出不希望是归一化到 [0,1] 之间，但是在计算 loss 时又需要归一化到 [0,1] 之间。

主要参数：

weight：各输出类别的 loss 权值设置
pos_weight：==设置输入样本类别对应的神经元的输出的 loss 权值==
ignore_index：忽略某个类别
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

1.5 nn.L1Loss

1	nn.L1Loss(size_average=None, reduce=None, reduction='mean')

功能：计算 inputs 与 target 之差的绝对值

主要参数：

reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

公式： $l_{n}=\left|x_{n}-y_{n}\right|$

1.6 nn.MSELoss

功能：计算 inputs 与 target 之差的平方

公式： $l_{n}=\left(x_{n}-y_{n}\right)^{2}$

主要参数：

reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

1.7 nn.SmoothL1Loss

1	nn.SmoothL1Loss(size_average=None, reduce=None, reduction='mean')

功能：平滑的 L1Loss

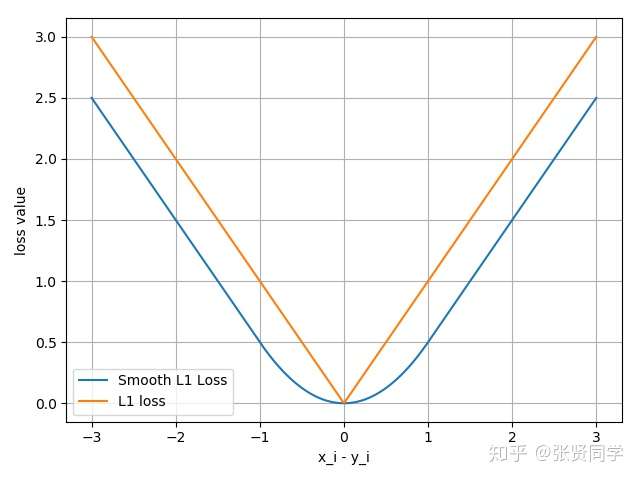
公式： $z_{i}=\left\{\begin{array}{ll}0.5\left(x_{i}-y_{i}\right)^{2}, & \text { if }\left|x_{i}-y_{i}\right|<1 \\ \left|x_{i}-y_{i}\right|-0.5, & \text { otherwise }\end{array}\right.$

下图中橙色曲线是 L1Loss，蓝色曲线是 Smooth L1Loss

主要参数：

reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

1.8 nn.PoissonNLLLoss

1	nn.PoissonNLLLoss(log_input=True, full=False, size_average=None, eps=1e-08, reduce=None, reduction='mean')

功能：泊松分布的负对数似然损失函数

主要参数：

log_input：输入是否为对数形式，决定计算公式
- 当 log_input = True，表示输入数据已经是经过对数运算之后的，loss(input, target) = exp(input) - target * input
- 当 log_input = False，，表示输入数据还没有取对数，loss(input, target) = input - target * log(input+eps)
full：计算所有 loss，默认为 loss
eps：修正项，避免 log(input) 为 nan

1.9 nn.KLDivLoss

1	nn.KLDivLoss(size_average=None, reduce=None, reduction='mean')

功能：计算 KLD(divergence)，KL 散度，相对熵

注意事项：需要提前将输入计算 log-probabilities，如通过nn.logsoftmax()

主要参数：

reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)，batchmean(batchsize 维度求平均值)

公式： $\begin{aligned} D_{K L}(P \| Q)=E_{x-p}\left[\log \frac{P(x)}{Q(x)}\right] &=E_{x-p}[\log P(x)-\log Q(x)] =\sum_{i=1}^{N} P\left(x_{i}\right)\left(\log P\left(x_{i}\right)-\log Q\left(x_{i}\right)\right) \end{aligned}$

对于每个样本来说，计算公式如下，其中 $y_{n}$ 是真实值 $P(x)$ ， $x_{n}$ 是经过对数运算之后的预测值 $logQ(x)$ 。

1.10 nn.MarginRankingLoss

1	nn.MarginRankingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能：计算两个向量之间的相似度，用于排序任务

特别说明：该方法计算两组数据之间的差异，返回一个 $n \times n$ 的 loss 矩阵

主要参数：

margin：边界值， $x_{1}$ 与 $x_{2}$ 之间的差异值
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

计算公式： $\operatorname{loss}(x, y)=\max (0,-y *(x 1-x 2)+\operatorname{margin})$ ， $y$ 的取值有 +1 和 -1。

当 $y=1$ 时，希望 $x_{1} > x_{2}$ ，当 $x_{1} > x_{2}$ ，不产生 loss
当 $y=-1$ 时，希望 $x_{1} < x_{2}$ ，当 $x_{1} < x_{2}$ ，不产生 loss

1.11 nn.SoftMarginLoss

1	nn.SoftMarginLoss(size_average=None, reduce=None, reduction='mean')

功能：计算二分类的 logistic 损失

主要参数：

reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

计算公式： $\operatorname{loss}(x, y)=\sum_{i} \frac{\log (1+\exp (-y[i] * x[i]))}{\text { x.nelement } 0}$

1.12 nn.MultiMarginLoss

1	nn.MultiMarginLoss(p=1, margin=1.0, weight=None, size_average=None, reduce=None, reduction='mean')

功能：计算多分类的折页损失

主要参数：

p：可以选择 1 或 2
weight：各类别的 loss 权值设置
margin：边界值
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

计算公式： $\operatorname{loss}(x, y)=\frac{\left.\sum_{i} \max (0, \operatorname{margin}-x[y]+x[i])\right)^{p}}{\quad \text { x.size }(0)}$ ，其中 y 表示真实标签对应的神经元输出，x 表示其他神经元的输出。

1.13 nn.CosineEmbeddingLoss

1	torch.nn.CosineEmbeddingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

功能：采用余弦相似度计算两个输入的相似性

主要参数：

margin：边界值，可取值 [-1, 1]，推荐为 [0, 0.5]
reduction：计算模式，，可以为 none(逐个元素计算)，sum(所有元素求和，返回标量)，mean(加权平均，返回标量)

计算公式： $\operatorname{loss}(x, y)=\left\{\begin{array}{ll}1-\cos \left(x_{1}, x_{2}\right), & \text { if } y=1 \\ \max \left(0, \cos \left(x_{1}, x_{2}\right)-\operatorname{margin}\right), & \text { if } y=-1\end{array}\right.$

其中 $\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}$

二、损失函数Q&A

2.1 nn.CrossEntropyLoss = softmax(x)+log(x)+nn.NLLLoss?

在各种深度学习框架中，我们最常用的损失函数就是交叉熵（torch.nn.CrossEntropyLoss），熵是用来描述一个系统的混乱程度,通过交叉熵我们就能够确定预测数据与真是数据之间的相近程度。交叉熵越小，表示数据越接近真实样本。

交叉熵计算公式：

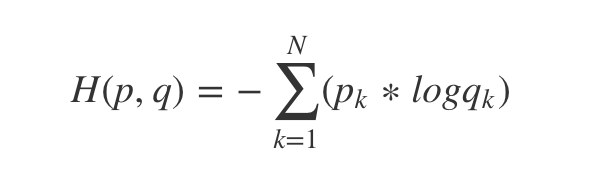
softmax函数又称为归一化指数函数，它可以把一个多维向量压缩在（0，1）之间，并且它们的和为1.

计算公式：

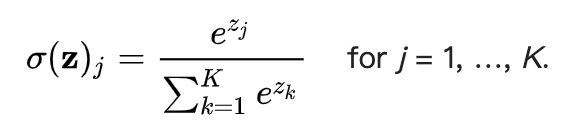
import math
z = [1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0]
z_exp = [math.exp(i) for i in z]  
print(z_exp)  # Result: [2.72, 7.39, 20.09, 54.6, 2.72, 7.39, 20.09] 
sum_z_exp = sum(z_exp)  
print(sum_z_exp)  # Result: 114.98 
softmax = [round(i / sum_z_exp, 3) for i in z_exp]
print(softmax)  # Result: [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]

log_softmax是指在softmax函数的基础上，再进行一次log运算，此时结果有正有负，log函数的值域是负无穷到正无穷，当x在0—1之间的时候，log(x)值在负无穷到0之间。

nn.NLLLoss的结果就是把上面的输出与Label对应的那个值拿出来，再去掉负号，再求均值。

import torch
input=torch.randn(3,3)
soft_input = torch.nn.Softmax(dim=0)
soft_input(input)
Out[20]: 
tensor([[0.7284, 0.7364, 0.3343],
        [0.1565, 0.0365, 0.0408],
        [0.1150, 0.2270, 0.6250]])

#对softmax结果取log
torch.log(soft_input(input))
Out[21]: 
tensor([[-0.3168, -0.3059, -1.0958],
        [-1.8546, -3.3093, -3.1995],
        [-2.1625, -1.4827, -0.4701]])

假设标签是[0,1,2]，第一行取第0个元素，第二行取第1个，第三行取第2个，去掉负号，即[0.3168,3.3093,0.4701],求平均值，就可以得到损失值。

(0.3168+3.3093+0.4701)/3
Out[22]: 1.3654000000000002
#验证一下
loss=torch.nn.NLLLoss()
target=torch.tensor([0,1,2])
loss(input,target)
Out[26]: tensor(0.1365)

nn.CrossEntropyLoss

loss=torch.nn.NLLLoss()
target=torch.tensor([0,1,2])
loss(input,target)
Out[26]: tensor(-0.1399)
loss =torch.nn.CrossEntropyLoss()
input = torch.tensor([[ 1.1879,  1.0780,  0.5312],
        [-0.3499, -1.9253, -1.5725],
        [-0.6578, -0.0987,  1.1570]])
target = torch.tensor([0,1,2])
loss(input,target)
Out[30]: tensor(0.1365)