算法长征（11）动态规划

发表于 更新于 分类于 ， 阅读次数： 本文字数： 14k 阅读时长 ≈ 25 分钟

img

首先，动态规划问题的一般形式就是==求最值==。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。求解动态规划的核心问题是穷举。首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「==备忘录」或者「DP table」==来优化穷举过程，避免不必要的计算。而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的「状态转移方程」，才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我研究出来的一个思维框架，辅助你思考状态转移方程：

1
2
3
4
5
6
7
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

5.1 背包问题

https://leetcode-cn.com/problems/coin-change/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-wan-q-80r7/

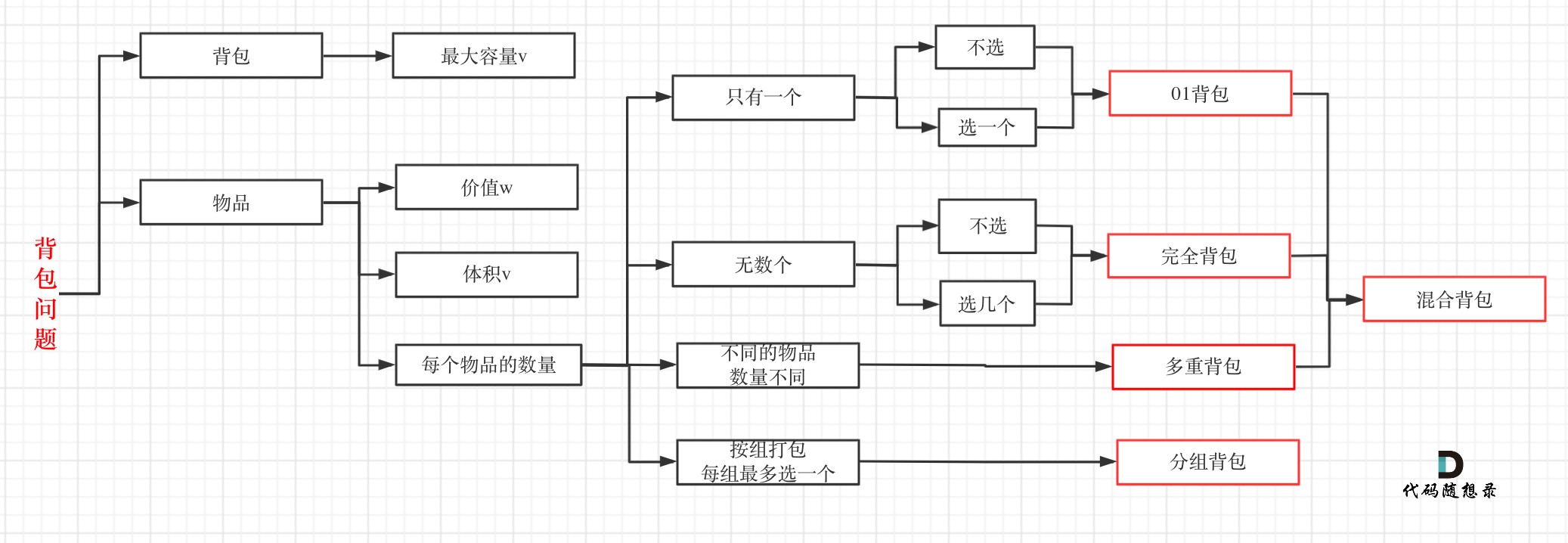
416.分割等和子集1

1、确定dp数组以及下标的含义

2、确定递推公式

3、dp数组如何初始化

  • 最大长度
  • 递推等号左侧要初始化

4、确定遍历顺序

  • 滚动数组

5、举例推导dp数组

5.1.1 背包递推公式

问==能否装满背包==（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

==问装满背包有几种方法==：dp[j] += dp[j - nums[i]] ，对应题目如下：

问背包装满==最大价值==：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

问装满背包所有物品的==最小个数==：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

5.1.2 遍历顺序

01背包

在动态规划：关于01背包问题，你该了解这些！ (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

和动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的，大家需要注意！

完全背包

说完01背包，再看看完全背包。

在动态规划：关于完全背包，你该了解这些！ (opens new window)中，讲解了纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求==组合数==就是外层for循环遍历物品，内层for遍历背包。

如果==求排列数==就是外层for遍历背包，内层for循环遍历物品。

相关题目如下：

如果求最小数，那么两层for循环的先后顺序就无所谓了，相关题目如下：

对于背包问题，其实递推公式算是容易的，难是难在遍历顺序上，如果把遍历顺序搞透，才算是真正理解了。

5.2 子序列（数组）问题

img

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

1
2
3
4
5
6
7
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp = [0 for _ in range(len(nums))]
        dp[0] = nums[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1] + nums[i], nums[i])
        return max(dp)

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

  • 动态规划 位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
  • 贪心 + 二分查找 tail[i] : 记录i长度的末尾是什么
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        dp = [1] * len(nums)
        result = 0
        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[j] < numa[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
            result = max(result, dp[i]) #取长的子序列
        return result
     def lengthOfLIS(self, nums: List[int]) -> int:
        # 贪心 + 二分查找 tail[i] : 记录i长度的末尾是什么
        tails, res = [0] * len(nums), 0
        for num in nums:
            i = bisect.bisect_left(tails[:res], num)
            """左边界
            while i < j:
                mid = (i + j)//2
                if tails[m] < num:
                    i = m + 1 
                else:
                    j = m
            """
            tails[i] = num
            if i == res:
                res += 1
        return res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def lenLongestFibSubseq(self, A: List[int]) -> int:
    # 基本顺序是 k，i，j 或者 A[k] = A[j] - A[i]
    n = len(A)
    dic = {}
    # 创建索引字典，提速
    for ind,val in enumerate(A):
        dic[val] = ind
    # 初始化，行代表的是i，不需要取到n-1，为了给j留出位置
    # 初始为2，只要包含了 j i 位置，则意味着已经有了2个数字。
    dp = [[2]*n for _ in range(n-1)]
    ret = 0
    # 因此i只能取到n-2，给j留出空间
    for i in range(1,n-1):
        # j从i+1开始，毕竟j在i后面
        for j in range(i+1,n):
            diff = A[j] - A[i]
            if diff in dic and dic[diff] < i:
                k = dic[diff]
                dp[i][j] = dp[k][i] + 1 # 这个1，代表着k位置数字
                ret = max(ret,dp[i][j])
    return ret

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def findLength(self, A: List[int], B: List[int]) -> int:
        dp = [0] * (len(B) + 1)
        result = 0
        for i in range(1, len(A)+1):
            for j in range(len(B), 0, -1):
                if A[i-1] == B[j-1]:
                    dp[j] = dp[j-1] + 1
                else:
                    dp[j] = 0 #注意这里不相等的时候要有赋0的操作
                result = max(result, dp[j])
        return result

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[m][n]

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 最长子序列 
        m, n = len(text1), len(text2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                if text2[j-1] == text1[i-1]:
                    dp[i][j] = dp[i-1][j-1] +1 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

动态规划：最大子序和 【贪心】【动态规划】

1
2
3
4
5
6
7
8
9
10
11
def maxSubArray(self, nums: List[int]) -> int:
    # 为什么dp[-1]不是最大？需要res
    # dp[i] 以i结尾的最大子数组和
    n = len(nums)
    if n == 0:
        return 0
    dp = [0] * (n)
    dp[0] = nums[0]
    for i in range(1, n):
        dp[i] = max(dp[i-1]+nums[i], nums[i])
    return max(dp)

动态规划：判断子序列 【双指针】

1
2
3
4
5
6
7
8
9
class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        n, m = len(s), len(t)
        i = j = 0
        while i < n and j < m:
            if s[i] == t[j]:
                i += 1
            j += 1
        return i == n

动态规划：不同的子序列

动态规划：两个字符串的删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# dp[i][j] : word1[i-1], word1[j-1] 最少步数
# word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况 *  min(dp[i-1][j], dp[i][j-1])+1  
  def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(n+1):
            dp[0][i] = i
        for j in range(m+1):
            dp[j][0] = j
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1])+1 # , dp[i-1][j-1]+1
        return dp[-1][-1]

动态规划：编辑距离

为了绝杀编辑距离，我做了三步铺垫，你都知道么？

给定一个字符串 s ，请计算这个字符串中有多少个回文子字符串。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

  • 动态规划、双指针+中心扩展、==Manacher算法==
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def countSubstrings(self, s: str) -> int:
        # 双指针+中心扩散
        result = 0
        def _extend(s, i, j, n):
            res = 0
            while i >= 0 and j < n and s[i] == s[j]: # 确定中心点
                i -= 1
                j += 1
                res += 1 # 扩散过程也是答案
            return res
        for i in range(len(s)):
            result += _extend(s, i, i, len(s)) #以i为中心
            result += _extend(s, i, i+1, len(s)) #以i和i+1为中心
        return result

    def countSubstrings(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 是否为回文子串
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 
        n = len(s)
        dp = [[False] * (n) for _ in range(n)]
        ans = 0
        for i in range(n-1,-1,-1):
            for j in range(i,n):
                if s[i] == s[j]:
                    if j - i <= 1:
                        ans += 1
                        dp[i][j] = True
                    elif dp[i+1][j-1]:
                        ans += 1
                        dp[i][j] = True
        return ans

最长回文子串 ==[Manacher 算法]==

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 中心扩展法
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 枚举+中心扩展法
        def extendCenter(left, right):
            while 0 <= left and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            # 返回的为while不成立的值
            return left+1, right-1 
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = extendCenter(i,i)
            left2, right2 = extendCenter(i,i+1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start:end+1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def longestPalindrome(self, s: str) -> str:
    # dp[i][j]: 是否是回文 dp[i+1][j-1] -> dp[i][j]
    # 返回的子串，不是数字 不能记录长度
    n = len(s)
    dp = [[False] * n for _ in range(n)] # 右上为1
    for i in range(n):
        dp[i][i] = True
    begin = 0
    maxlen = 0
    # 判断是否是回文子串中，如果是则记录begin and len
    for i in range(n-1, -1,-1):
        for j in range(i,n):
            if s[i] == s[j]:
                if j - i <=1:
                    dp[i][j] = True
                elif dp[i+1][j-1]:
                    dp[i][j] = True
            
            if dp[i][j] and j - i + 1 > maxlen:
                maxlen = j - i + 1
                begin = i

    return s[begin:begin+maxlen]

  • Manacher 算法：Manacher 算法是在线性时间内求解最长回文子串的算法。在本题中，我们要求解回文串的个数，为什么也能使用 Manacher 算法呢？这里我们就需要理解一下 Manacher 的基本原理。

    • 奇偶长度处理： abaaabaa 会被处理成 #a#b#a#a##a#b#a#a#

    • ==\(f(i)\) 来表示以 s 的第 i 位为回文中心，可以拓展出的最大回文半径 （包括 # ）==，那么$ f(i) - 1$就是以 i 为中心的最大回文串长度 。

    • 利用已经计算出来的状态来更新 f(i）：回文右端点rm ：i + f(i) - 1

动态规划：最长回文子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 最大回文长度
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 and j - i >=2
        n = len(s)
        dp = [[0] * i +[1] * (n-i) for i in range(n)] # 从定义出发 右上三角 = 1 有意义
        for i in range(n-1,-1,-1):
            for j in range(i+1,n): # j - i >=2
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2 
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])                
        return dp[0][n-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def minCut(self, s: str) -> int:
        # 动态规划1:判断回文
        n = len(s)
        g = [[True] * n for _ in range(n)]

        for i in range(n - 1, -1, -1):
            for j in range(i + 1, n):
                g[i][j] = (s[i] == s[j]) and g[i + 1][j - 1]
        # 
        f = [float("inf")] * n
        for i in range(n):

            if g[0][i]:
                f[i] = 0
            else:
                for j in range(i):
                    if g[j + 1][i]:
                        # （0, j) + (j+1, i)
                        f[i] = min(f[i], f[j] + 1)
        
        return f[n - 1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        # 动态规划
        dic, res = dict(), 0
        for num in nums:
            if num not in dic:
                left, right = dic.get(num - 1, 0), dic.get(num + 1,0)
                cur = 1 + left +right
                if res < cur:
                    res = cur
                dic[num] = cur
                dic[num - left] = cur
                dic[num + right] = cur
        return res

5.3 打家劫舍问题

5.4 股票问题

股票问题总结

动态规划：121.买卖股票的最佳时机(opens new window)

股票只能买卖一次，问最大利润

  • 动态规划、贪心算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
      	# 动态规划
        if not prices:
            return 0
        dp = [[0] * 2 for _ in range(len(prices))] 
        dp[0][0] = -prices[0]# 已持有的状态
        dp[0][1] = 0 # 未持有的状态
        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i-1][0], -prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]
    def maxProfit(self, prices: List[int]) -> int:
        # 贪心算法
        if not prices:
            return 0
        buy, profit = prices[0], 0
        for i in range(1, len(prices)):
            profit = max(profit, prices[i] - buy)
            if prices[i] < buy:
                buy = prices[i]
        return profit

动态规划：122.买卖股票的最佳时机II(opens new window) 可以多次买卖股票，问最大收益。

动态规划：123.买卖股票的最佳时机III(opens new window) 最多买卖两次，问最大收益。

动态规划：188.买卖股票的最佳时机IV(opens new window) 最多买卖k笔交易，问最大收益。

动态规划：309.最佳买卖股票时机含冷冻期(opens new window) 可以多次买卖但每次卖出有冷冻期1天。

动态规划：714.买卖股票的最佳时机含手续费(opens new window) 可以多次买卖，但每次有手续费。

5.5 编辑距离问题

判断子序列

动态规划：392.判断子序列 (opens new window)给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

这道题目 其实是可以用双指针或者贪心的的，但是我在开篇的时候就说了这是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

  • if (s[i - 1] == t[j - 1])
    • t中找到了一个字符在s中也出现了
  • if (s[i - 1] != t[j - 1])
    • 相当于t要删除元素，继续匹配

状态转移方程：

1
2
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];

不同的子序列

动态规划：115.不同的子序列 (opens new window)给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

本题虽然也只有删除操作，不用考虑替换增加之类的，但相对于动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了。

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为 dp[i - 1] [j - 1]

一部分是不用s[i - 1]来匹配，个数为 dp[i - 1] [j]

1
2
3
4
5
if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

动态规划：583.两个字符串的删除操作 (opens new window)给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

本题和动态规划：115.不同的子序列 (opens new window)相比，其实就是两个字符串可以都可以删除了，情况虽说复杂一些，但整体思路是不变的。

  • 当word1[i - 1] 与 word2[j - 1]相同的时候
  • 当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1] [j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1] [j] + 1

情况二：删word2[j - 1]，最少操作次数为dp [i] [j - 1] + 1

1
2
3
4
5
if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

动态规划：72.编辑距离 (opens new window)给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

编辑距离终于来了，有了前面三道题目的铺垫，应该有思路了，本题是两个字符串可以增删改，比 动态规划：判断子序列 (opens new window)，动态规划：不同的子序列 (opens new window)，动态规划：两个字符串的删除操作 (opens new window)都要复杂的多。

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

  • if (word1[i - 1] == word2[j - 1])
    • 不操作
  • if (word1[i - 1] != word2[j - 1])
    • 增
    • 删
    • 换

也就是如上四种情况。

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1] [j - 1]，即dp[i][j] = dp[i - 1] [j - 1];

在整个动规的过程中，最为关键就是正确理解dp[i] [j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离 加上一个增加元素的操作。

即 dp[i][j] = dp[i - 1] [j] + 1;

操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个增加元素的操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是添加元素，删除元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word2添加一个元素d，也就是相当于word1删除一个元素d，操作数是一样！

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1] [j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i] [j] = min({dp[i - 1] [j - 1], dp[i - 1] [j], dp[i][j - 1]}) + 1;

1
2
3
4
5
6
if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

==让字符串成为最小回文==

https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/

请实现一个函数用来匹配包含'. '和''的正则表达式。模式中的字符'.'表示任意一个字符，而' '表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但与"aa.a"和"ab*a"均不匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        # 【dp含义】dp[i][j] : s[:i - 1] 可以正则匹配 p[:j - 1]
        m, n = len(s), len(p)
        # 【初始化】
        dp = [[False] * (n + 1) for _ in range(m + 1)]
        dp[0][0] = True
        for j in range(2, n + 1, 2):
            dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
        # 【遍历顺序】
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                # 【状态转移推导】
                if p[j - 1] == '*': 
                    if dp[i][j - 2]:
                        dp[i][j] = True
                    elif dp[i - 1][j] and (p[j - 2] == '.' or s[i - 1] == p[j - 2]):
                        dp[i][j] = True
                else:
                    if dp[i-1][j-1] and (p[j - 1] == '.' or s[i - 1] == p[j - 1]):
                        dp[i][j] = True
                
        return dp[-1][-1]

六、其他

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。【求三角矩阵非对角线】

  • 动态规划双向遍历
1
2
3
4
5
6
7
8
9
class Solution:
    def constructArr(self, a: List[int]) -> List[int]:
        b, tmp = [1] * len(a), 1
        for i in range(1, len(a)):
            b[i] = b[i - 1] * a[i - 1] # 下三角
        for i in range(len(a) - 2, -1, -1):
            tmp *= a[i + 1]            # 上三角
            b[i] *= tmp                # 下三角 * 上三角
        return b

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

  • 三指针、优先队列（质数的线性筛算法）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def nthUglyNumber(self, n: int) -> int:
        # 维护3个 2，3，5的动态个数
        dp = [0] * (n + 1)
        dp[1] = 1
        p2 = p3 = p5 = 1
        for i in range(2, n + 1):
          	# 
            u2, u3, u5 = 2 * dp[p2], 3 * dp[p3], 5 * dp[p5]
            dp[i] = min(u2, u3, u5)
            if dp[i] == u5:
                p5 += 1
            if dp[i] == u3:
                p3 += 1
            if dp[i] == u2:
                p2 += 1
        return dp[-1]
    def nthUglyNumber(self, n: int) -> int:
        if n == 1:
            return 1
        H = [(2, 2), (3, 3), (5, 5)]
        heapify(H)
        for i in range(n - 1):
            num, p = heappop(H)
            heappush(H, (num * 2, 2))
            if p >= 3:
                heappush(H, (num * 3, 3))
                if p >= 5:
                    heappush(H, (num * 5, 5))
        #print(len(H)) #n = 1670时, H长度为162
        return num

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

  • 已知n - 1个骰子的解为f(n - 1), 添加一个骰子，求n个骰子的点数和为x的概率f（n， x）

image-20220608212653374

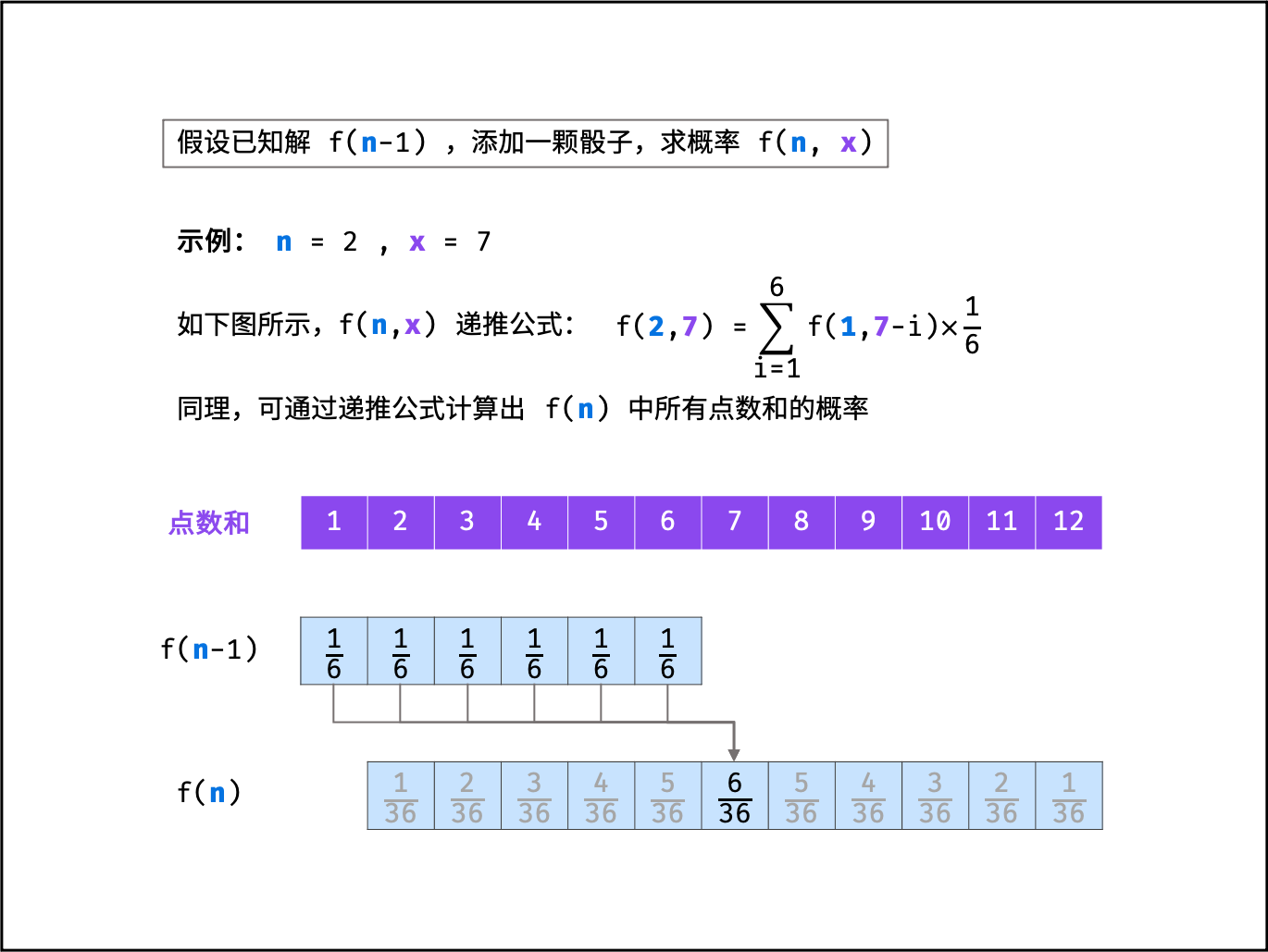
Picture2.png

1
2
3
4
5
6
7
8
9
10
class Solution:
    def dicesProbability(self, n: int) -> List[float]:
        dp = [1 / 6] * 6
        for i in range(2, n + 1):
            tmp = [0] * (5 * i + 1)
            for j in range(len(dp)):
                for k in range(6): # 防止越界
                    tmp[j + k] += dp[j] / 6
            dp = tmp
        return dp