深度学习（6）LSTM*

发表于 2022-03-16 更新于 2022-07-13 分类于算法，【draft】深度学习， RNN 阅读次数：本文字数： 9.6k 阅读时长 ≈ 17 分钟

LSTM和GRU算法简单梳理🍭

前言 - 从反向传播推导到梯度消失and爆炸的原因及解决方案？

从反向传播推导到梯度消失and爆炸的原因及解决方案（从DNN到RNN，内附详细反向传播公式推导） - 韦伟的文章 - 知乎 https://zhuanlan.zhihu.com/p/76772734

本质上是因为神经网络的更新方法，梯度消失是因为反向传播过程中对梯度的求解会产生sigmoid导数和参数的连乘，sigmoid导数的最大值为0.25，权重一般初始都在0，1之间，乘积小于1，多层的话就会有多个小于1的值连乘，导致靠近输入层的梯度几乎为0，得不到更新。梯度爆炸是也是同样的原因，只是如果初始权重大于1，或者更大一些，多个大于1的值连乘，将会很大或溢出，导致梯度更新过大，模型无法收敛。其实梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。

一、反向传播推导到梯度消失and爆炸的原因及解决方案

1.1 ==反向传播推导：==

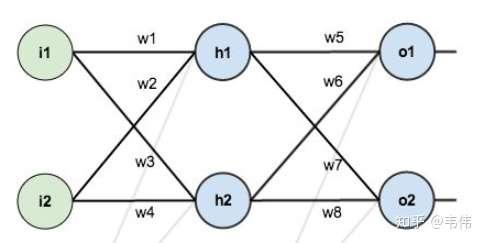
以上图为例开始推起来，先说明几点，i1，i2是输入节点，h1，h2为隐藏层节点，o1，o2为输出层节点，除了输入层，其他两层的节点结构为下图所示：

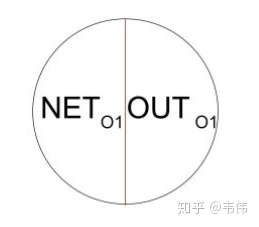
举例说明， $NET_{o1}$ 为输出层的输入，也就是隐藏层的输出经过线性变换后的值， $OUT_{o1}$ 为经过激活函数sigmoid后的值；同理 $NET_{h1}$ 为隐藏层的输入，也就是输入层经过线性变换后的值， $OUT_{h1}$ 为经过激活函数sigmoid 的值。只有这两层有激活函数，输入层没有。

定义一下sigmoid的函数： $\sigma(z) =\frac{1}{1+e^{-z}}$ 说一下sigmoid的求导：

定义一下损失函数，这里的损失函数是均方误差函数，即：

具体到上图，就是：

到这里，所有前提就交代清楚了，前向传播就不推了，默认大家都会，下面推反向传播。

第一个反向传播（热身）

先来一个简单的热热身，求一下损失函数对W5的偏导，即： $\frac{\partial Loss_{t o t a l}}{\partial w_5}$

首先根据链式求导法则写出对W5求偏导的总公式，再把图拿下来对照（如上），可以看出，需要计算三部分的求导【损失函数、激活函数、线性函数】，下面就一步一步来：

综上三个步骤，得到总公式：

第二个反向传播：

接下来，要求损失函数对w1的偏导，即： $\frac{\partial Loss_{t o t a l}}{\partial w_1}$

还是把图摆在这，方便看，先写出总公式，对w1求导有个地方要注意，w1的影响不仅来自o1还来自o2，从图上可以一目了然，所以总公式为：

所以总共分为左右两个式子，分别又对应5个步骤，详细写一下左边，右边同理：

$第一步： \frac{\partial Loss_{t o t a l}}{\partial out_{o1}} = out_{o1} - target_1\\$ $第二步： \frac{\partial out_{o1}}{\partial net_{o1}} = \sigma(net_{o1})(1-\sigma(net_{o1})) \\$

右边也是同理，就不详细写了，写一下总的公式：

这个公式只是对如此简单的一个网络结构的一个节点的偏导，就这么复杂。。亲自推完才深深的意识到。。。

为了后面描述方便，把上面的公式化简一下， $out_{o1} - target_1$ 记为 $C_{o1}$ ， $\sigma(net_{o1})(1-\sigma(net_{o1}))$ 记为 $\sigma(net_{o1})^{\prime}$ ，则：

1.2 ==梯度消失，爆炸产生原因：==

从上式其实已经能看出来，求和操作其实不影响，主要是是看乘法操作就可以说明问题，可以看出，损失函数对w1的偏导，与 $C_{o1}$ ，权重w，sigmoid的导数有关，明明还有输入i为什么不提？因为如果是多层神经网络的中间某层的某个节点，那么就没有输入什么事了。所以产生影响的就是刚刚提的三个因素。

再详细点描述，如图，多层神经网络：

参考：PENG：神经网络训练中的梯度消失与梯度爆炸282 赞同 · 26 评论文章

假设（假设每一层只有一个神经元且对于每一层 $y_i=\sigma\left(z_i\right)=\sigma\left(w_ix_i+b_i\right)$ ，其中 $\sigma$ 为sigmoid函数），如图：

则：

看一下sigmoid函数的求导之后的样子：

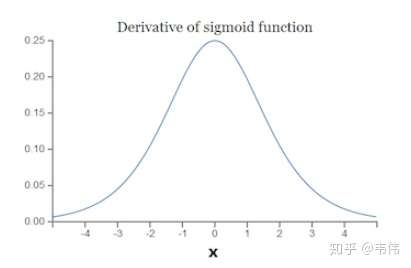
发现sigmoid函数求导后最大最大也只能是0.25。

再来看W，一般我们初始化权重参数W时，通常都小于1，用的最多的应该是0，1正态分布吧。

所以 $|\sigma'\left(z\right)w|\leq0.25$ ，多个小于1的数连乘之后，那将会越来越小，导致靠近输入层的层的权重的偏导几乎为0，也就是说几乎不更新，这就是梯度消失的根本原因。

再来看看梯度爆炸的原因，也就是说如果 $|\sigma'\left(z\right)w|\geq1$ 时，连乘下来就会导致梯度过大，导致梯度更新幅度特别大，可能会溢出，导致模型无法收敛。sigmoid的函数是不可能大于1了，上图看的很清楚，那只能是w了，这也就是经常看到别人博客里的一句话，初始权重过大，一直不理解为啥。。现在明白了。

但梯度爆炸的情况一般不会发生，对于sigmoid函数来说， $\sigma(z)^{\prime}$ 的大小也与w有关，因为 $z=wx+b$ ，除非该层的输入值 $x$ 在一直一个比较小的范围内。

其实梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。

==所以，总结一下，为什么会发生梯度爆炸和消失：==

本质上是因为神经网络的更新方法，梯度消失是因为反向传播过程中对梯度的求解会产生sigmoid导数和参数的连乘，sigmoid导数的最大值为0.25，权重一般初始都在0，1之间，乘积小于1，多层的话就会有多个小于1的值连乘，导致靠近输入层的梯度几乎为0，得不到更新。梯度爆炸是也是同样的原因，只是如果初始权重大于1，或者更大一些，多个大于1的值连乘，将会很大或溢出，导致梯度更新过大，模型无法收敛。

1.3 梯度消失、爆炸解决方案？

参考：DoubleV：详解深度学习中的梯度消失、爆炸原因及其解决方法

预训练加微调

梯度剪切、正则

解决方案一（预训练加微调）：

提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。

Hinton在训练深度信念网络（Deep Belief Networks中，使用了这个方法，在各层预训练完成后，再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一定的好处，但是目前应用的不是很多了。

解决方案二（梯度剪切、正则）：

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。

正则化是通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式：

其中， $\alpha$ 是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。

注：事实上，在深度神经网络中，往往是梯度消失出现的更多一些

解决方案三（改变激活函数）：

首先说明一点，tanh激活函数不能有效的改善这个问题，先来看tanh的形式：

再来看tanh的导数图像：

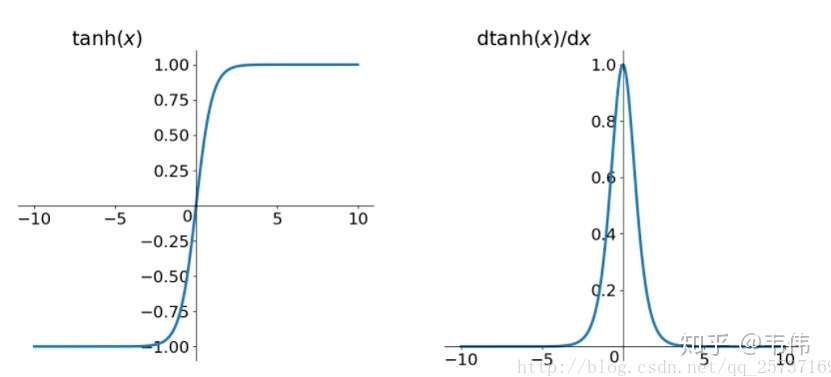
发现虽然比sigmoid的好一点，sigmoid的最大值小于0.25，tanh的最大值小于1，但仍是小于1的，所以并不能解决这个问题。

Relu:思想也很简单，如果激活函数的导数为1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度，relu就这样应运而生。先看一下relu的数学表达式：

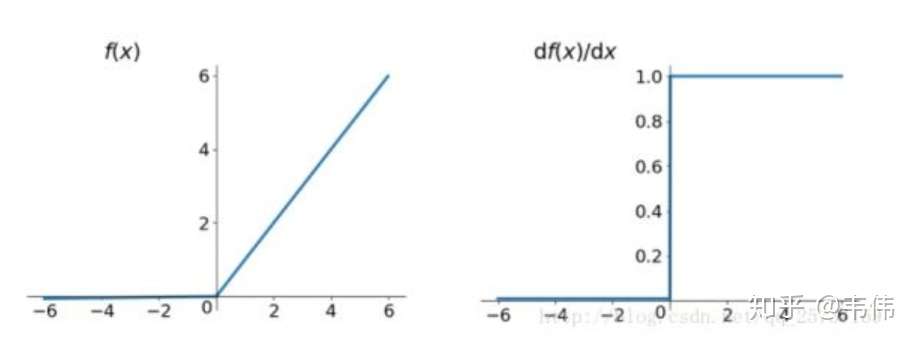
从上图中，我们可以很容易看出，relu函数的导数在正数部分是恒等于1的，因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。

relu的主要贡献在于：

解决了梯度消失、爆炸的问题
计算方便，计算速度快
加速了网络的训练

同时也存在一些缺点：

由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）
输出不是以0为中心的

leakrelu

leakrelu就是为了解决relu的0区间带来的影响，其数学表达为： $leakrelu=\begin{equation} f(x)= \begin{cases} x, & {x\gt 0} \\\\ x*k, & {x\leq 0} \end{cases} \end{equation}$ 其中k是leak系数，一般选择0.1或者0.2，或者通过学习而来解决死神经元的问题。

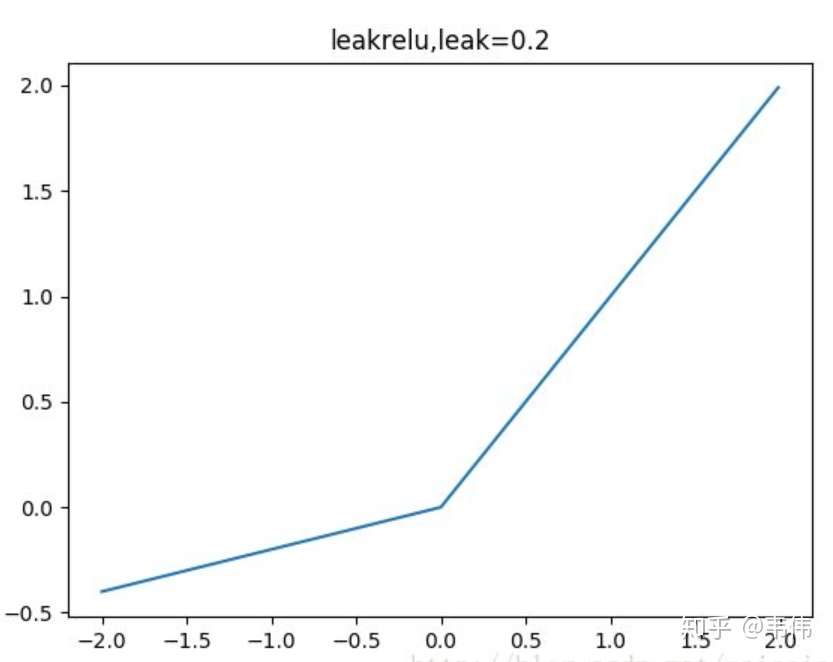
leakrelu解决了0区间带来的影响，而且包含了relu的所有优点

elu

elu激活函数也是为了解决relu的0区间带来的影响，其数学表达为：

其函数及其导数数学形式为：

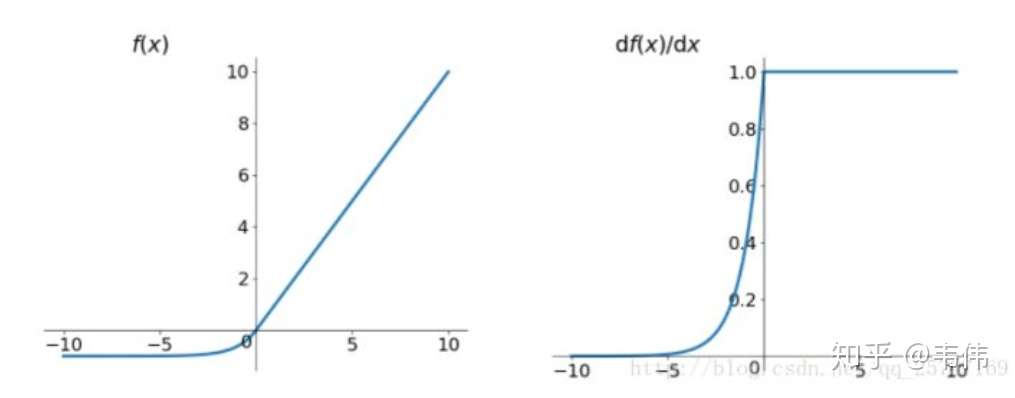
但是elu相对于leakrelu来说，计算要更耗时间一些，因为有e。

解决方案四（batchnorm）：【梯度消失】

Batchnorm是深度学习发展以来提出的最重要的成果之一了，目前已经被广泛的应用到了各大网络中，具有加速网络收敛速度，提升训练稳定性的效果，Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization，简称BN，即批规范化，通过规范化操作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。

具体的batchnorm原理非常复杂，在这里不做详细展开，此部分大概讲一下batchnorm解决梯度的问题上。具体来说就是反向传播中，经过每一层的梯度会乘以该层的权重，举个简单例子：正向传播中 $f_3=f_2(w^T*x+b)$ ，那么反向传播中， $\frac {\partial f_2}{\partial x}=\frac{\partial f_2}{\partial f_1}w$ ，反向传播式子中有w的存在，所以 $w$ 的大小影响了梯度的消失和爆炸，batchnorm就是通过对每一层的输出做scale和shift的方法，通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布【假设原始是正态分布】强行拉回到接近均值为0方差为1的标准正太分布，即严重偏离的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，使得让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

解决方案五（残差结构）：

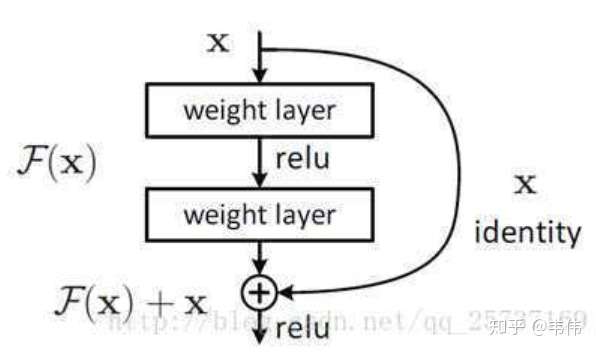
如图，把输入加入到某层中，这样求导时，总会有个1在，这样就不会梯度消失了。

式子的第一个因子 $\frac{\partial loss}{\partial {{x}_{L}}}$ 表示的损失函数到达 L 的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易。

注：上面的推导并不是严格的证，只为帮助理解

==解决方案六（LSTM）：==

在介绍这个方案之前，有必要来推导一下RNN的反向传播，因为关于梯度消失的含义它跟DNN不一样！不一样！不一样！

先推导再来说，从这copy的：沉默中的思索：RNN梯度消失和爆炸的原因565 赞同

RNN结构如图：

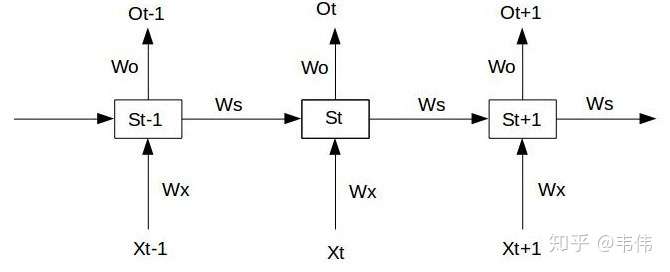
假设我们的时间序列只有三段， $S_{0}$ 为给定值，神经元没有激活函数，则RNN最简单的前向传播过程如下： $S_{1}=W_{x}X_{1}+W_{s}S_{0}+b_{1}$ $O_{1}=W_{o}S_{1}+b_{2}$

$S_{2}=W_{x}X_{2}+W_{s}S_{1}+b_{1}$ $O_{2}=W_{o}S_{2}+b_{2}$

$S_{3}=W_{x}X_{3}+W_{s}S_{2}+b_{1}$ $O_{3}=W_{o}S_{3}+b_{2}$

假设在t=3时刻，损失函数为 $L_{3}=\frac{1}{2}(Y_{3}-O_{3})^{2}$ 。

则对于一次训练任务的损失函数为 $L=\sum_{t=0}^{T}{L_{t}}$ ，即每一时刻损失值的累加。

使用随机梯度下降法训练RNN其实就是对 $W_{x}$ 、 $W_{s}$ 、 $W_{o}$ 以及 $b_{1}$ $b_{2}$ 求偏导，并不断调整它们以使L尽可能达到最小的过程。

现在假设我们我们的时间序列只有三段，t1，t2，t3。

我们只对t3时刻的 $W_{x}、W_{s}、W_{0}$ 求偏导（其他时刻类似）：

可以看出对于 $W_{0}$ 求偏导并没有长期依赖，但是对于 $W_{x}、W_{s}$ 求偏导，会随着时间序列产生长期依赖。因为 $S_{t}$ 随着时间序列向前传播，而 $S_{t}$ 又是 $W_{x}、W_{s}$ 的函数。

根据上述求偏导的过程，我们可以得出任意时刻对 $W_{x}、W_{s}$ 求偏导的公式：

任意时刻对 $W_{s}$ 求偏导的公式同上。

如果加上激活函数， $S_{j}=tanh(W_{x}X_{j}+W_{s}S_{j-1}+b_{1})$ ，则 $\prod_{j=k+1}^{t}{\frac{\partial{S_{j}}}{\partial{S_{j-1}}}}$ = $\prod_{j=k+1}^{t}{tanh^{'}}W_{s}$ 激活函数tanh和它的导数图像在上面已经说过了，所以原因在这就不赘述了，还是一样的，激活函数导数小于1。

==现在来解释一下，为什么说RNN和DNN的梯度消失问题含义不一样？==

先来说DNN中的反向传播：在上文的DNN反向传播中，我推导了两个权重的梯度，第一个梯度是直接连接着输出层的梯度，求解起来并没有梯度消失或爆炸的问题，因为它没有连乘，只需要计算一步。第二个梯度出现了连乘，也就是说越靠近输入层的权重，梯度消失或爆炸的问题越严重，可能就会消失会爆炸。一句话总结一下，DNN中各个权重的梯度是独立的，该消失的就会消失，不会消失的就不会消失。

再来说RNN：RNN的特殊性在于，它的权重是共享的。抛开W_o不谈，因为它在某时刻的梯度不会出现问题（某时刻并不依赖于前面的时刻），但是W_s和W_x就不一样了，每一时刻都由前面所有时刻共同决定，是一个相加的过程，这样的话就有个问题，当距离长了，计算最前面的导数时，最前面的导数就会消失或爆炸，但当前时刻整体的梯度并不会消失，因为它是求和的过程，当下的梯度总会在，只是前面的梯度没了，但是更新时，由于权值共享，所以整体的梯度还是会更新，通常人们所说的梯度消失就是指的这个，指的是当下梯度更新时，用不到前面的信息了，因为距离长了，前面的梯度就会消失，也就是没有前面的信息了，但要知道，整体的梯度并不会消失，因为当下的梯度还在，并没有消失。

一句话概括：RNN的梯度不会消失，RNN的梯度消失指的是当下梯度用不到前面的梯度了，但DNN靠近输入的权重的梯度是真的会消失。

说完了RNN的反向传播及梯度消失的含义，终于该说为什么LSTM可以解决这个问题了，这里默认大家都懂LSTM的结构，对结构不做过多的描述。见第三节。【LSTM通过它的“门控装置”有效的缓解了这个问题，这也就是为什么我们现在都在使用LSTM而非普通RNN。】

二、LSTM 框架结构

前言：

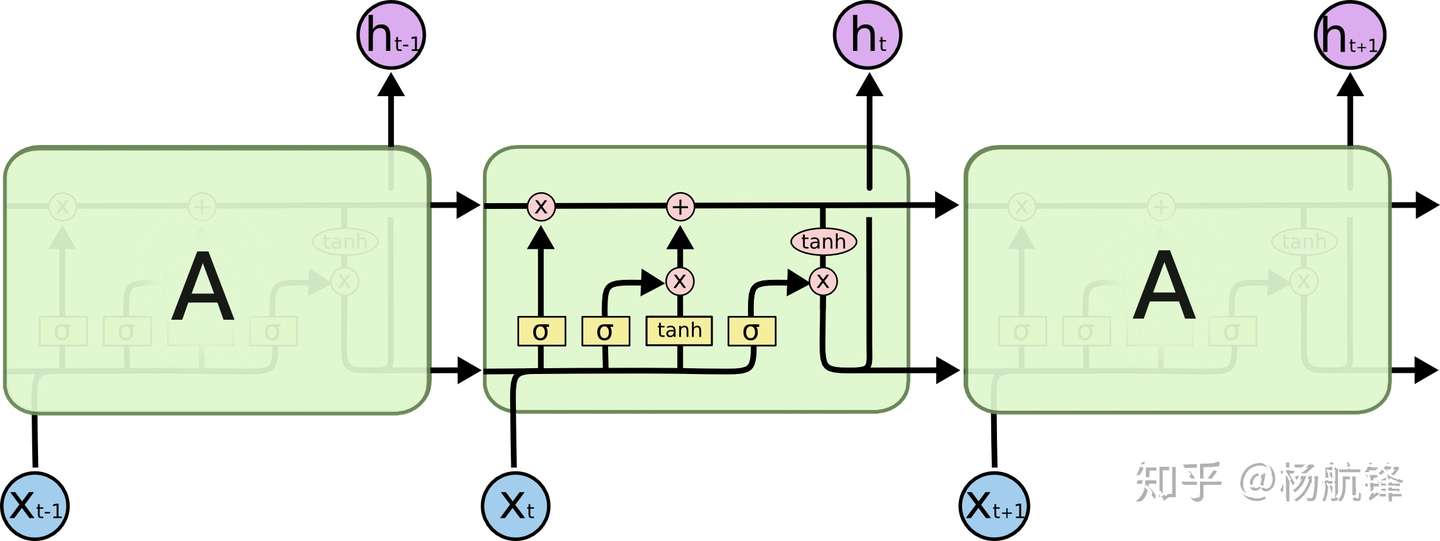
LSTM是RNN的一种变体，更高级的RNN，那么它的本质还是一样的，还记得RNN的特点吗，可以有效的处理序列数据，当然LSTM也可以，还记得RNN是如何处理有效数据的吗，是不是每个时刻都会把隐藏层的值存下来，到下一时刻的时候再拿出来用，这样就保证了，每一时刻含有上一时刻的信息，如图，我们把存每一时刻信息的地方叫做Memory Cell，中文就是记忆细胞，可以这么理解。

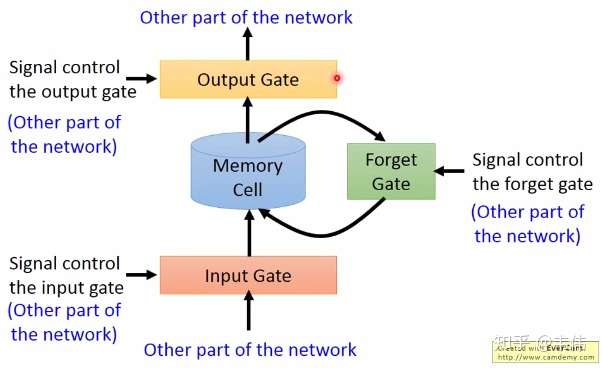
RNN什么信息它都存下来，因为它没有挑选的能力，而LSTM不一样，它会选择性的存储信息，因为它能力强，它有门控装置，它可以尽情的选择。如下图，普通RNN只有中间的Memory Cell用来存所有的信息，而从下图我们可以看到，LSTM多了三个Gate。

Input Gate：输入门，在每一时刻从输入层输入的信息会首先经过输入门，输入门的开关会决定这一时刻是否会有信息输入到Memory Cell。

Output Gate：输出门，每一时刻是否有信息从Memory Cell输出取决于这一道门。

Forget Gate：遗忘门，每一时刻Memory Cell里的值都会经历一个是否被遗忘的过程，就是由该门控制的，如果打卡，那么将会把Memory Cell里的值清除，也就是遗忘掉。

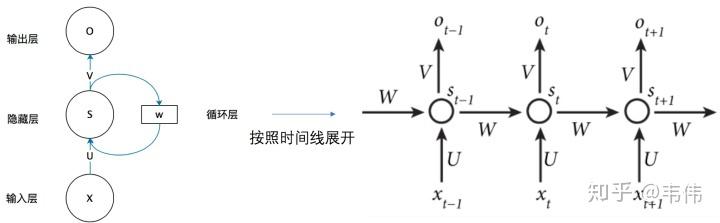
在了解LSTM的内部结构之前，我们需要先回顾一下普通RNN的结构，以免在这里很多读者被搞懵，如下：

我们可以看到，左边是为了简便描述RNN的工作原理而画的缩略图，右边是展开之后，每个时间点之间的流程图，注意，我们接下来看到的LSTM的结构图，是一个时间点上的内部结构，就是整个工作流程中的其中一个时间点，也就是如下图：

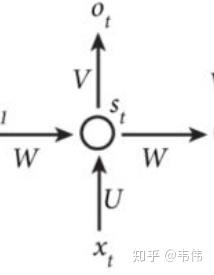
注意，上图是普通RNN的一个时间点的内部结构，上面已经讲过了公式和原理，LSTM的内部结构更为复杂，不过如果这么类比来学习，我认为也没有那么难。

Cell：memory cell，也就是一个记忆存储的地方，这里就类似于普通RNN的 $S_t$ ，都是用来存储信息的，这里面的信息都会保存到下一时刻，其实标准的叫法应该是 $h_t$ ，因为这里对应神经网络里的隐藏层，所以是hidden的缩写，无论普通RNN还是LSTM其实t时刻的记忆细胞里存的信息，都应该被称为 $h_t$

$a$ 是这一时刻的输出，也就是类似于普通RNN里的 $O_t$

四个 $Z，Z_i，Z_f，Z_o$ ，这四个相辅相成，才造就了中间的Memory Cell里的值，你肯恩要问普通RNN里有个 $X_t$ 作为输入，那LSTM的输入在哪？别着急，其实这四个 $Z，Z_i，Z_f，Z_o$ 都有输入向量 $X_t$ 的参与。对了，在解释这四个分别是什么之前，我要先解释一下上图的所有这个符号：都代表一个激活函数，LSTM里常用的激活函数有两个，一个是tanh，一个是sigmoid。

$Z=tanh(W[x_t,h_{t-1}])\\Z_i=\sigma(W_i[x_t,h_{t-1}])\\Z_f=\sigma(W_f[x_t,h_{t-1}])\\Z_o=\sigma(W_o[x_t,h_{t-1}])\\$

$Z$ 是最为普通的输入，可以从上图中看到， $Z$ 是通过该时刻的输入 $X_t$ 和上一时刻存在memory cell里的隐藏层信息 $h_{t-1}$ 向量拼接，再与权重参数向量 $W$ 点积，得到的值经过激活函数tanh最终会得到一个数值。

$Z_i$ input gate的缩写i，所以也就是输入门的门控装置， $Z_i$ 同样也是通过该时刻的输入 $X_t$ 和上一时刻隐藏状态，也就是上一时刻存下来的信息 $h_{t-1}$ 向量拼接，在与权重参数向量 $W_i$ 点积（注意每个门的权重向量都不一样，这里的下标i代表input的意思，也就是输入门)。得到的值经过激活函数sigmoid的最终会得到一个0-1之间的一个数值，用来作为输入门的控制信号。

以此类推，就不详细讲解 $Z_f，Z_o$ 了，分别是缩写forget和output的门控装置，原理与上述输入门的门控装置类似。上面说了，只有 $Z$ 是输入，其他的三个都是门控装置，负责把控每一阶段的信息记录与遗忘，具体是怎样的呢？我们先来看公式：首先解释一下，经过这个sigmod激活函数后，得到的 $Z_i，Z_f，Z_o$ 都是在0到1之间的数值，1表示该门完全打开，0表示该门完全关闭，

==LSTM迭代过程==

LSTM和GRU算法简单梳理🍭: https://zhuanlan.zhihu.com/p/72500407

$h_{t}$ ：当前序列的隐藏状态、 $x_{t}$ ：当前序列的输入数据、 $C_{t}$ ：当前序列的细胞状态、 $\sigma$ ： $sigmoid$ 激活函数、 $\tanh$ ： $\tanh$ 激活函数。

遗忘门：

输入门：

细胞状态更新：

输出门：

2.1 LSTM之遗忘门

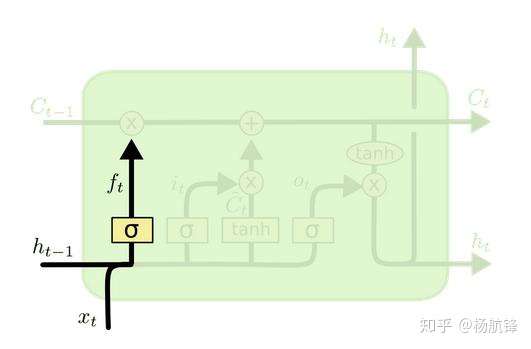
遗忘门是控制是否遗忘的，在 $LSTM$ 中即以一定的概率控制是否遗忘上一层的细胞状态。图中输入的有前一序列的隐藏状态 $h_{t-1}$ 和当前序列的输入数据 $x_t$ ，通过一个 $sigmoid$ 激活函数得到遗忘门的输出 $f_t$ 。因为 $sigmoid$ 函数的取值在 $[0, 1]$ 之间，所以 $f_t$ 表示的是遗忘前一序列细胞状态的概率，数学表达式为

2.2 LSTM之输入门

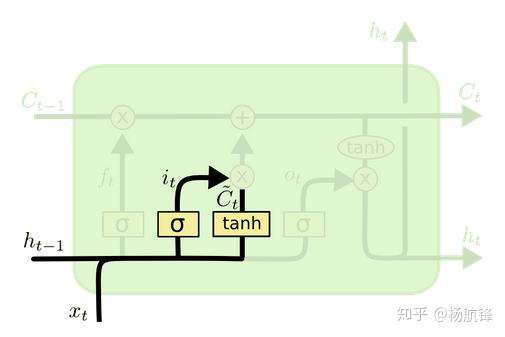
输入门是用来决定哪些数据是需要更新的，由 $sigmoid$ 层决定；然后，一个 $\tanh$ 层为新的候选值创建一个向量 $\tilde{C_t}$ ，这些值能够加入到当前细胞状态中，数学表达式为

2.3 LSTM之细胞状态更新

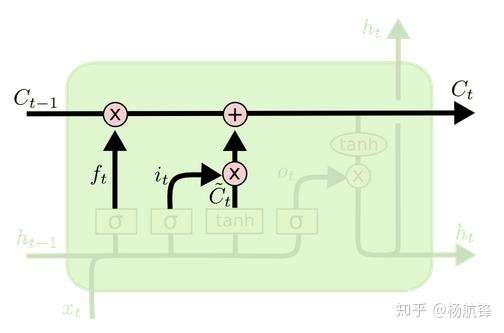
前面的遗忘门和输入门的结果都会作用于细胞状态 $C_t$ ，在决定需要遗忘和需要加入的记忆之后，就可以更新前一序列的细胞状态 $C_{t-1}$ 到当前细胞状态 $C_t$ 了，前一序列的细胞状态 $C_{t-1}$ 乘以遗忘门的输出 $f_t$ 表示决定遗忘的信息， $i_t\odot \tilde{C_t}$ 表示新的记忆信息，数学表达式为：

2.4 LSTM之输出门

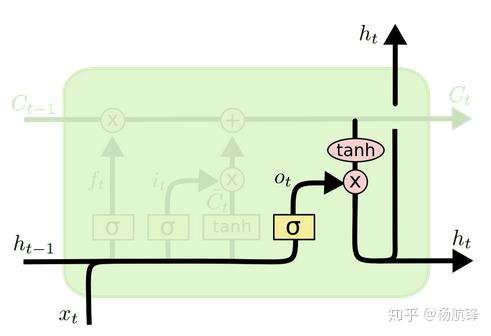
在得到当前序列的细胞状态 $C_t$ 后，就可以计算当前序列的输出隐藏状态 $h_t$ 了，隐藏状态 $h_t$ 的更新由两部分组成，第一部分是 $o_t$ ，它由前一序列的隐藏状态 $h_{t-1}$ 和当前序列的输入数据 $x_t$ 通过激活函数 $sigmoid$ 得到，第二部分由当前序列的细胞状态 $C_t$ 经过 $\tanh$ 激活函数后的结果组成，数学表达式为

三、GRU 框架结构

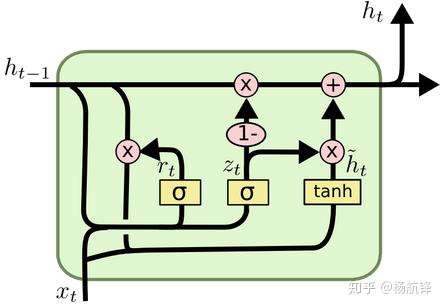
循环门单元( $Gated\ Recurrent\ Unit,\ GRU$ )，它组合了遗忘门和输入门到一个单独的更新门当中，也合并了细胞状态 $C$ 和隐藏状态 $h$ ，并且还做了一些其他的改变使得其模型比标准 $LSTM$ 模型更简单，其数学表达式式为： $\begin{equation} \begin{aligned} z_{t} &=\sigma\left(W_{z} \cdot\left[h_{t-1}, x_{t}\right]\right) \\ r_{t} &=\sigma\left(W_{r} \cdot\left[h_{t-1}, x_{t}\right]\right) \\ \tilde{h}_{t} &=\tanh \left(W \cdot\left[r_{t} \odot h_{t-1}, x_{t}\right]\right) \\ h_{t} &=\left(1-z_{t}\right) \odot h_{t-1}+z_{t} \odot \tilde{h}_{t} \end{aligned} \end{equation}\\$

首先介绍 $GRU$ 的两个门，它们分别是重置门 $r_t$ 和更新门 $z_t$ ，计算方法与 $LSTM$ 中门的计算方法是一致的；然后是计算候选隐藏层 $\tilde{h}_t$ ，该候选隐藏层和 $LSTM$ 中的 $\tilde{C}_t$ 类似，都可以看成是当前时刻的新信息，其中 $r_t$ 用来控制需要保留多少之前的记忆，如果 $r_t$ 为 $0$ 则表示 $\tilde{h}_t$ 只保留当前序列的输入信息；最后 $z_t$ 控制需要从前一序列的隐藏层 $h_{t-1}$ 中遗忘多少信息和需要加入多少当前序列的隐藏层信息 $\tilde{h}_t$ ，从而得到当前序列的输出隐藏层信息 $h_t$ ，而 $GRU$ 是没有输出门的。

GRU和LSTM的性能差不多，但GRU参数更少，更简单，所以训练效率更高。但是，如果数据的依赖特别长且数据量很大的话，LSTM的效果可能会稍微好一点，毕竟参数量更多。所以默认推荐使用LSTM。

参考资料⬇️

Understanding LSTM Networks

LSTM Q&A

1、为什么LSTM可以解决梯度消失和梯度爆炸？

参考（这个老哥说的是最好的）：LSTM如何来避免梯度弥散和梯度爆炸？

==LSTM 中梯度的传播有很多条路径， $c_{t-1} \rightarrow c_t = f_t\odot c_{t-1} + i_t \odot \hat{c_t}$ 这条路径上只有逐元素相乘和相加的操作，梯度流最稳定==；但是其他路径（例如 $c_{t-1} \rightarrow h_{t-1} \rightarrow i_t \rightarrow c_t$ )上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。
LSTM 刚提出时没有遗忘门，或者说相当于 $f_t=1$ ，这时候在 $c_{t-1} \rightarrow c_t$ 直接相连的短路路径上， $dl/dc_t$ 可以无损地传递给 $dl/dc_{t-1}$ ，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。
但是在其他路径上，LSTM 的梯度流和普通 RNN 没有太大区别，依然会爆炸或者消失。由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。
同样，因为总的远距离梯度 = 各条路径的远距离梯度之和，高速公路上梯度流比较稳定，但其他路径上梯度有可能爆炸，此时总的远距离梯度 = 正常梯度 + 爆炸梯度 = 爆炸梯度，因此 LSTM 仍然有可能发生梯度爆炸。不过，==由于 LSTM 的其他路径非常崎岖，和普通 RNN 相比多经过了很多次激活函数（导数都小于 1），因此 LSTM 发生梯度爆炸的频率要低得多==。实践中梯度爆炸一般通过梯度裁剪来解决。
对于现在常用的带遗忘门的 LSTM 来说，4 中的分析依然成立，而 3 分为两种情况：其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。

2、为什么LSTM模型中既存在sigmoid又存在tanh两种激活函数？

关于激活函数的选取，在LSTM中，遗忘门、输入门和输出门使用 Sigmoid函数作为激活函数;在生成候选记忆时，使用双曲正切函数tanh作为激活函数。值得注意的是，这两个激活函数都是饱和的也就是说在输入达到一定值的情况下，输出就不会发生明显变化了。如果是用非饱和的激活图数，例如ReLU，那么将难以实现门控的效果。

Sigmoid的输出在0-1之同，符合门控的物理定义，且当输入较大或较小时，其输出会非常接近1或0，从而保证该门开或关，在生成候选记亿时，
tanh函数，是因为其输出在-1-1之间，这与大多数场景下特征分布是0中心的吻合。此外，tanh函数在输入为0近相比 Sigmoid函数有更大的梯度，通常使模型收敛更快。

激活函数的选择也不是一成不变的。例如在原始的LSTM中，使用的激活函数是 Sigmoid函数的变种，h(x)=2sigmoid(x)-1,g(x)＝4 sigmoid(x)-2，这两个函数的范国分别是[-1，1]和[-2，2]。并且在原始的LSTM中，只有输入门和输出门，没有遗忘门，其中输入经过输入门后是直接与记忆相加的，所以输入门控g(x)的值是0中心的。

后来经过大量的研究和实验，人们发现增加遗忘门对LSTM的性能有很大的提升且h(x)使用tanh比2 sigmoid(x)-1要好，所以现代的LSTM采用 Sigmoid和tanh作为激活函数。事实上在门控中，使用 Sigmoid函数是几乎所有现代神经网络模块的共同选择。例如在门控循环单元和注意力机制中，也广泛使用 Sigmoid i函数作为门控的激活函数。

为什么？

门是控制开闭的，全开时值为1，全闭值为０。用于遗忘和保留信息。
对于求值的激活函数无特殊要求。

能更换吗？

门是控制开闭的，全开时值为1，全闭值为０。用于遗忘和保留信息。门的激活函数只能是值域为０到１的，最常见的就是sigmoid。
对于求值的激活函数无特殊要求。

3、能不能把tanh换成relu？

不行？对于梯度爆炸的问题用梯度裁剪解决就行了。

会造成输出值爆炸。RNN共享参数矩阵，长程的话相当于多个相乘，最后输出类似于 $f\left[W \ldots\left[W f\left[W f\left[W f_{i}\right]\right]\right]\right]$ ，其中是 $f$ 激活函数，如果 $W$ 有一个大于1的特征值，且使用relu激活函数，那最后的输出值会爆炸。但是使用tanh激活函数，能够把输出值限制在-1和1之间。
这里relu并不能解决梯度消失或梯度爆炸的问题。假设有t=3，最后一项输出反向传播对W求导， $\frac{\partial f_{3}}{\partial W_{1}}=\frac{\partial f_{3}}{\partial a_{3}} f_{2}+\frac{\partial f_{3}}{\partial a_{3}} W \frac{\partial f_{2}}{\partial a_{2}} f_{1}+\frac{\partial f_{3}}{\partial a_{3}} W \frac{\partial f_{2}}{\partial a_{2}} W \frac{\partial f_{1}}{\partial a_{1}} \frac{\partial a_{1}}{\partial W_{1}}$ 。我们用最后一项做分析，即使使用了relu， $\frac{\partial f_{3}}{\partial a_{3}}=\frac{\partial f_{2}}{\partial a_{2}}=\frac{\partial f_{3}}{\partial a_{1}}=1$ ，还是会有两个 $W$ 相乘，并不能解决梯度消失或梯度爆炸的问题。