理论基础(6)特征归一化
一、机器学习的特征归一化方法
在迈入深度神经网络之前,本文主要介绍下传统机器学习中有哪些特征归一化方法。
1.1 常见的特征归一化
上文我们讲了特征归一化,就是要让各个特征有相似的尺度。相似的尺度一般是讲要有相似的取值范围。因此我们可以通过一些方法把特征的取值范围约束到一个相同的区间。另一方面,这个尺度也可以理解为这些特征都是从一个相似的分布中采样得来。因此我们还可以通过一些方法使得不同特征的取值均符合相似的分布。这里我们介绍一些常见的特征归一化方法的细节,原理和实现。
(1) rescaling (min-max normalization, range scaling) \[ x^{\prime}=a+\frac{(x-\min (\mathrm{x}))(\mathrm{b}-\mathrm{a})}{\max (\mathrm{x})-\min (\mathrm{x})} \] 这里是把每一维的值都映射到目标区间 \([a, b]\) 。一般常用的目标区间是 \([0,1],[-1,1]\) 。特别的, 映射到0和1区 间的的计算方式为: \(x^{\prime}=\frac{x-\min (\mathrm{x})}{\max (\mathrm{x})-\min (\mathrm{x})}\) 。
(2) mean normalization
\(x^{\prime}=\frac{x-\mu}{\max (\mathrm{x})-\min (\mathrm{x})}\) 。这里 \(\mu\) 指的向量的均值。与上面不同的是, 这里减去的是均值。这样能够保证向量中所有元素的均值为 0 。
(3) 标准化 standard normalization (z-score normalization)
\(x^{\prime}=\frac{x-\mu}{\sigma}\) 。这里 \(\sigma\) 指的是向量的标准差。更常见的是这种, 使得所有元素的均值为 0 , 方差为 1 。
(4) scaling to unit length
\(x^{\prime}=\frac{x}{\|x\|}\) 。这里是把向量除以其长度, 即对向量的长度进行归一化。长度度量一般采用 \(\mathrm{L}\) 范数或者 \(L 2\) 范数。
范数(英语:Norm),是具有“长度"概念的函数。在线性代数、泛函分析及相关的数学领域, 是一个函数, 其为向量空间内的所有向量赋予非零的正长度或大小。 \(L p(p=1 . . n)\) 范数: \(\|x\|_p:=\left(\sum_{i=1}^n x_i^p\right)^{1 / p}\) 。
1.2 原理
总结来看,前三种特征归一化方法的计算方式是减一个统计量再除以一个统计量,最后一种为除以向量自身的长度。
- 减去一个统计量可以看做选哪个值作为原点(是最小值或者均值),然后将整个数据集都平移到这个新的原点位置。如果特征之间的偏置不同会对后续过程产生负面影响,则该操作是有益的,可以看做某种偏置无关操作。如果原始特征值是有特殊意义的,则该操作可能会有害。如何理解:对于一堆二维数据,计算均值得到(a,b),减去这个均值点,就相当于把整个平面直角坐标系平移到这个点上,为什么呢?因为(a,b)-(a,b) = (0,0)就是原点,其他的点在x轴和y轴上做相应移动。
- 除以一个统计量可以看做在坐标轴方向上对特征进行缩放,用于降低特征尺度的影响,可以看做某种特征无关操作。缩放可以采用最大值和最小值之间的跨度,也可以用标准差(到中心点的平均距离)。如何理解:(a,b)/ 3 = (a/3, b/3),就相当于这些点在x轴上的值缩小三倍,在y轴上缩小三倍。
- 除以长度相当于把长度归一化,把所有特征都映射到单位球上,可以看作某种长度无关操作。比如词频特征要移除文章长度的影响,图像处理中某些特征要移除光照强度的影响,以及方便计算向量余弦相似度等。如何理解:除以向量的模,实际就是让向量的长度为1,这样子,若干个n维向量就分布在一个单位球上,只是方向不同。
更直观地,可以从下图(来自于CS231n课程)观察上述方法的作用。下图是一堆二维数据点的可视化,可以看到,减去了每个维度的均值 以后,数据点的中心移动到了原点位置,进一步的,每个维度用标准差缩放以后,在每个维度上,数据点的取值范围均保持相同。
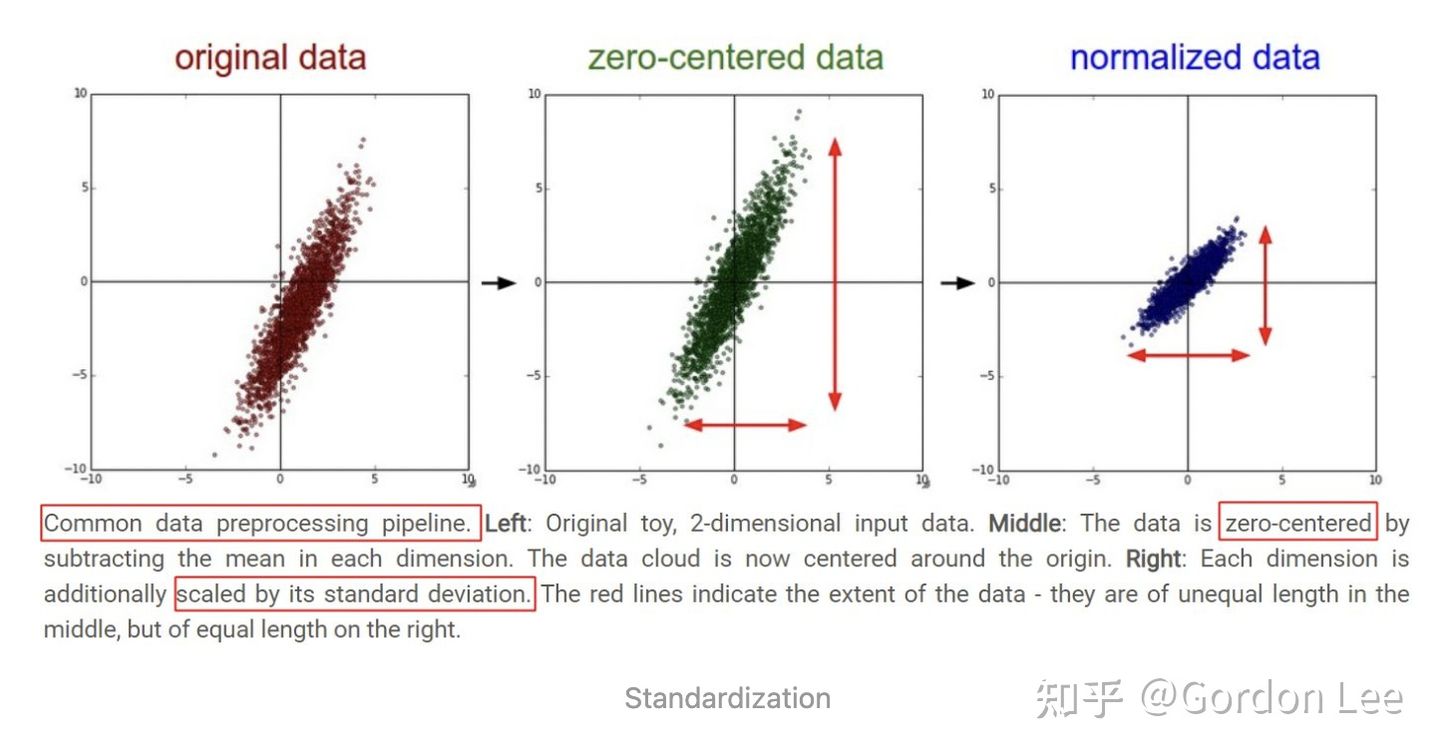
1.3 标准化和归一化
PCA、k-means、回归模型、神经网络
定义
归一化和标准化都是对数据做变换的方式,将原始的一列数据转换到某个范围,或者某种形态,具体的:
- 归一化(Normalization):将一列数据变化到某个固定区间(范围)中,通常,这个区间是[0, 1],广义的讲,可以是各种区间,比如映射到[0,1]一样可以继续映射到其他范围,图像中可能会映射到[0,255],其他情况可能映射到[-1,1];
- 标准化(Standardization):将数据变换为均值为0,标准差为1的分布切记,并非一定是正态的;
- 中心化:另外,还有一种处理叫做中心化,也叫零均值处理,就是将每个原始数据减去这些数据的均值。
差异
归一化:对处理后的数据范围有严格要求;
标准化: 数据不为稳定,存在极端的最大最小值; 涉及距离度量、协方差计算的时候;
- 归一化会严格的限定变换后数据的范围,比如按之前最大最小值处理的,它的范围严格在[ 0 , 1 ]之间;而标准化就没有严格的区间,变换后的数据没有范围,只是其均值是0,标准差为1。
- 归一化的缩放比例仅仅与极值有关,容易受到异常值的影响。
用处
- 可解释性:回归模型中自变量X的量纲不一致导致了回归系数无法直接解读或者错误解读;需要将X都处理到统一量纲下,这样才可比【可解释性】;取决于我们的逻辑回归是不是用了正则化。如果你不用正则,标准化并不是必须的,如果用正则,那么标准化是必须的。
- 距离计算:机器学习任务和统计学任务中有很多地方要用到“距离”的计算,比如PCA,比如KNN,比如kmeans等等,假使算欧式距离,不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果;
- 加速收敛:参数估计时使用梯度下降,在使用梯度下降的方法求解最优化问题时, 归一化/标准化后可以加快梯度下降的求解速度,即提升模型的收敛速度。
L1、L2正则化减少过拟合
其他:log、sigmod、softmax 变换
二、深度学习的特征归一化方法
今天我们开始介绍这些特征归一化方法在复杂的深度神经网络的作用
2.1 前置内容:Domain Adaption中的Covariate Shift
在讲传统机器学习的特征归一化在深度网络中的应用之前,先要讲下迁移学习中的领域自适应(DA)。在迁移学习中,源域有很多标注数据,目标域没有或者只有少量的标注数据,但是有大量无标注数据。比如常见的问题就是机器学习模型的泛化性问题,希望在A领域上训练的模型,能够在B领域也有比较好的性能。
在DA中, 一般假设源领域和目标领域有相同的样本空间, 比如猫狗分类问题, 样本空间就是两个类:猫和狗, 但是数据分布不同 \(p_s(x, y) \neq p_t(x, y)\) 。由贝叶斯公式可以把这个联合分布分解为 \[ p(x, y)=p(x \mid y) p(y)=p(y \mid x) p(x) \text { 。 } \] 所以数据分布不一致有3种情况:(具体可以看我的回答:在迁移学习中,边缘概率分布和条件概率分布有什么含义?)。这里主要介绍Covariate Shift现象。
variate指的是一个随机变量,co-variate指的是随这个随机变量变化的另一个随机变量。Covariate Shift指的就是:源领域和目标领域的输入边缘分布不同,但是条件分布相同 \(p_s(x) \neq p_t(x) ; p_s(y \mid x)=p_t(y \mid x)\)。以猫狗识别问题为例:
- 源领域中的狗都是哈士奇,而目标领域中的狗都是拉布拉多,所以输入的边缘分布不同。
- 不管是什么狗,最后输出为狗的概率都为1,也就是输出的label都要是狗,也就是条件分布相同,也就是学习任务是相同的。
- 解决这种情况的做法一般是学习一个domain invariant的representation,也就是不管是什么领域的狗,最后输出都要是狗这个标签。
2.2 深度神经网络中的归一化
把传统机器学习中的特征归一化方法用在具有多个隐藏层的深度神经网络中,对隐藏层的输入进行归一化,也能够提升训练效率。其”可能“的原因有几派的观点:
(1)更好的尺度不变性(即不同层输入的取值范围或者分布都比较一致)
一般上认为,深度神经网络中存在一种叫做internal covariate shift (ICS)的现象:在深度神经网络中,一个神经层的输入是之前神经层的输出。给定一个神经层,它之前的所有神经层的参数变化会导致其输入的分布发生较大的改变。当使用随机梯度下降来训练网络时,每次参数更新都会导致该神经层的输入分布发生改变。越高的层,其输入分布会改变得越明显.就像一栋高楼,低楼层发生一个较小的偏移,可能会导致高楼层较大的偏移。
该现象会导致下面几个问题:
- 在训练的过程中,网络需要不断适应新的输入数据分布(其实就是之前讲的梯度更新迭代步数增多),所以会大大降低学习速度。
- 由于参数的分布不同,所以可能导致很多数据落入梯度饱和区,使得学习过早停止。
- 某些参数分布偏离太大,对其他层或者输出产生了巨大影响。
对比上面的概念就是:在神经网络的各层输出,由于它们经过了层内操作作用,其分布显然与各层对应的输入分布不同,而且差异会随着网络深度增大而增大。各层的输入和输出分布可以看作源领域和目标领域的输入边缘分布(因为这一层的输出分布也是下一层的输入分布),显然这两个分布已经变的不同了,但是其要预测的条件分布是相同的,因为两个输入预测出来的最后的label肯定要是一样的。
为了缓解ICS问题,需要对隐藏层的输入进行归一化,比如都归一化成标准正态分布,可以使得每个神经层对其输入具有更好的尺度不变性.不论低层的参数如何变化,高层的输入保持相对稳定。
(2)更平滑的”优化地形“(optimization landscape)
在NIPS2018的How Does Batch Normalization Help Optimization?一文中,作者详细阐述了batch normalization (一种用在DNN上的归一化方法)真正起作用的原因。该文中对ICS有了更精要的阐述,即该层的输入分布会因为之前层的更新而发生改变。同时,论文提出了两个问题,即BN的作用是否与ICS相关,以及BN是否会消除或减少ICS。
为了探究第一个问题,作者在BN层后面人为引入了一个随时间随机改变(该分布不容易被DNN学到)的噪声分布(即人为引入漂移现象,使得下一层的分布不再稳定)。结果发现,加了噪声以后,层的分布的稳定性(通过可视化每层采样一定神经元的激活值来度量分布的方差和均值)并不好,但是最后的效果依然很好,这说明BN层和ICS似乎没有啥关系。(因为加了BN层,虽然分布不稳定,但是效果依然好)。
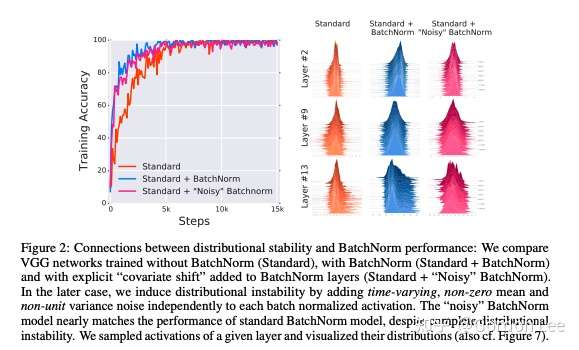
为了探究第二个问题,作者又设计了指标来量化ICS现象:通过测量更新到前一层和当前层的梯度差异(L2距离)来量化一个层中的参数在多大程度上必须“调整”以应对前一层中的参数更新。理想来说,ICS现象越小,上一层参数更新对当前层的分布影响越小,梯度变化程度越小。最后实验发现BN并不能减少ICS,甚至可能还会有一定程度上的增加。
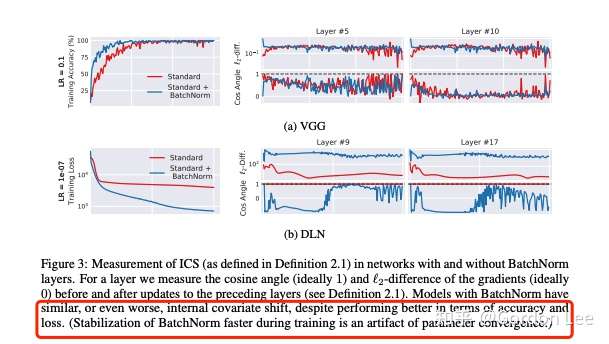
由此,作者认为BN层的作用可能和ICS没啥关系,也不能减少ICS。而作者认为,BN的作用在于使得optimization landscape更加光滑。
神经网络的高维损失函数构成了一个损失曲面,也被称为优化地形(optimization landscape)。这里用L-Lipschitz函数即\(\left|f\left(x_1\right)-f\left(x_2\right)\right| \leq L\left\|x_1-x_2\right\|\)来定量描述这种光滑度。作者发现确实加了BN层以后,optimization landscape更加光滑了。

进一步地,作者还以平滑优化地形为目标设计了另一种方法,结果发现和BN的效果差不多。这也说明了BN层的作用在于使得优化地形更加平滑。
2.3 总结
今天我们主要介绍了归一化方法(Batch Normalization)在深度神经网络中的作用:有人认为是更好的尺度不变性来缓解ICS现象。有人认为是更平滑的优化地形。当然,BN层究竟怎么起作用的,现在还是没太探究清楚。实际上,咱们还没开始介绍BN是什么!!!哈哈哈,下一篇文章俺们就从缓解ICS现象的角度来讲解BN的原理和实现,并和之前讲过的机器学习中的归一化方法进行关联。
参考文献
Transformer中的归一化(二):机器学习中的特征归一化方法 - Gordon Lee的文章 - 知乎 https://zhuanlan.zhihu.com/p/477116352
Transformer中的归一化(三):特征归一化在深度神经网络的作用 - Gordon Lee的文章 - 知乎 https://zhuanlan.zhihu.com/p/481179310