算法长征（3）二叉树

发表于 更新于 分类于 ， 阅读次数： 本文字数： 13k 阅读时长 ≈ 24 分钟

二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

  • 数组切片、字典递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        # 切片
        if len(preorder) == 0:
            return None
        rootVal = preorder[0]
        rootindex = inorder.index(rootVal)
        leftsize = rootindex
        root = TreeNode(rootVal)
        root.left = self.buildTree(preorder[1:leftsize+1], inorder[:rootindex])
        root.right = self.buildTree(preorder[leftsize+1:], inorder[rootindex+1:])
        return root

    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def recur(root, left, right):
            if left > right: return                               # 递归终止
            node = TreeNode(preorder[root])                       # 建立根节点
            i = dic[preorder[root]]                               # 划分根节点、左子树、右子树
            node.left = recur(root + 1, left, i - 1)              # 开启左子树递归
            node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归
            return node                                           # 回溯返回根节点

        dic = {val: i for i, val in enumerate(inorder)}
        return recur(0, 0, len(inorder) - 1)

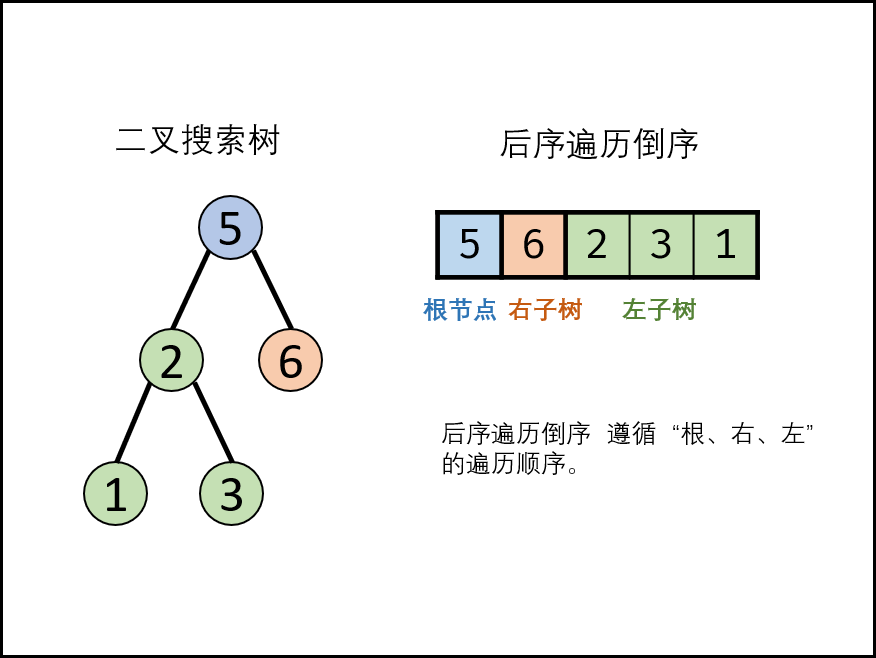
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

  • 分治、辅助单调栈

辅助单调栈：

Picture10.png

  • 借助一个单调栈 stack 存储值递增的节点；
  • 每当遇到值递减的节点 \(r_i\) ，则通过出栈来更新节点 \(r_i\)的父节点 \(root\) ；
  • 每轮判断 \(r_i和 root\)的值关系：
    • 若 \(r_i > root\)则说明不满足二叉搜索树定义，直接返回 false。
    • 若 \(r_i < root\) 则说明满足二叉搜索树定义，则继续遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
        if len(postorder) == 0:
            return True
        inorder = sorted(postorder)
        rootval = postorder[-1]
        rootindex = inorder.index(rootval)
        rightsize = len(inorder) - rootindex - 1
        if set(inorder[rootindex+1:]) != set(postorder[-1-rightsize:-1]):
            return False
        if set(inorder[:rootindex]) != set(postorder[:-1-rightsize]):
            return False
        return self.verifyPostorder(postorder[-1-rightsize:-1]) and self.verifyPostorder(postorder[:-1-rightsize])

    def verifyPostorder(self, postorder: [int]) -> bool:
        # 分治递归
        def recur(i, j):
            if i >= j: 
                return True
            p = i
            while postorder[p] < postorder[j]: 
                p += 1
            m = p
            while postorder[p] > postorder[j]: 
                p += 1
            return p == j and recur(i, m - 1) and recur(m, j - 1)

        return recur(0, len(postorder) - 1)
    
    def verifyPostorder(self, postorder: [int]) -> bool:
        # 单调队列
        stack, root = [], float("+inf")
        for i in range(len(postorder) - 1, -1, -1):
            if postorder[i] > root: return False
            while(stack and postorder[i] < stack[-1]):
                root = stack.pop()
            stack.append(postorder[i])
        return True

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def largestValues(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        q = deque([root])
        ans = []
        while q:
            k = len(q)
            tmp = float('-inf')
            for _ in range(k):
                node = q.popleft()
                if (t:= node.val) > tmp:
                    tmp = t
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            ans.append(tmp)
        return ans

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

  • 深度优先遍历、广度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        curVal = curHeight = 0
        def dfs(node: Optional[TreeNode], height: int) -> None:
            if node is None:
                return
            height += 1
            dfs(node.left, height)
            dfs(node.right, height)
            nonlocal curVal, curHeight
            if height > curHeight:
                curHeight = height
                curVal = node.val
        dfs(root, 0)
        return curVal
		def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        q = deque([root])
        while q:
            node = q.popleft()
            if node.right:
                q.append(node.right)
            if node.left:
                q.append(node.left)
            ans = node.val
        return ans

搜索

【层序遍历】

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
        if not root: return []
        res, queue = [], collections.deque()
        queue.append(root)
        while queue:
            node = queue.popleft()
            res.append(node.val)
            if node.left: queue.append(node.left)
            if node.right: queue.append(node.right)
        return res

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        ans, q = [], collections.deque()
        q.append(root)
        while q:
            tmp = []
            for i in range(len(q)):
                node = q.popleft()
                tmp.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            ans.append(tmp)
        return ans

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        ans, q = [], collections.deque()
        q.append(root)
        while q:
            tmp = []
            k = len(q)
            for _ in range(k):
                node = q.popleft()
                tmp.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            ans.append(tmp[::-1] if len(ans) % 2 else tmp)
        return ans

给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        left_high = self.maxDepth(root.left)
        right_high = self.maxDepth(root.right)
        return max(left_high, right_high)+1
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # 空树，高度为 0
        if root == None:
            return 0
        # 初始化队列和层次
        queue = [root]
        depth = 0
        # 当队列不为空
        while queue:
            # 当前层的节点数
            n = len(queue)
            # 弹出当前层的所有节点，并将所有子节点入队列
            for _ in range(n):
                node = queue.pop(0)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            depth += 1
        # 二叉树最大层次即为二叉树最深深度
        return depth

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return root
        stack = [root]
        while stack:
            node = stack.pop()
            node.left, node.right = node.right, node.left
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        return root
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        # 反转左右子树
        if not root:
            return root
        root.left, root.right = root.right, root.left
        root.left = self.mirrorTree(root.left)
        root.right = self.mirrorTree(root.right)
   
        return root

[辅助函数]

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)，B是A的子结构， 即 A中有出现和B相同的结构和节点值。

  • ==对称性递归==：https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof/solution/yi-pian-wen-zhang-dai-ni-chi-tou-dui-che-uhgs/
1
2
3
4
5
6
7
8
9
10
class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        def recur(A, B):
            if not B: 
              	return True
            if not A or A.val != B.val: 
              	return False
            return recur(A.left, B.left) and recur(A.right, B.right)

        return bool(A and B) and (recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B))

[辅助函数]

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        def recur(left, right):
            if not left and not right:
                return True
            if not left or not right or left.val != right.val:
                return False
            return recur(left.left, right.right) and recur(left.right, right.left)
        return recur(root.left, root.right)

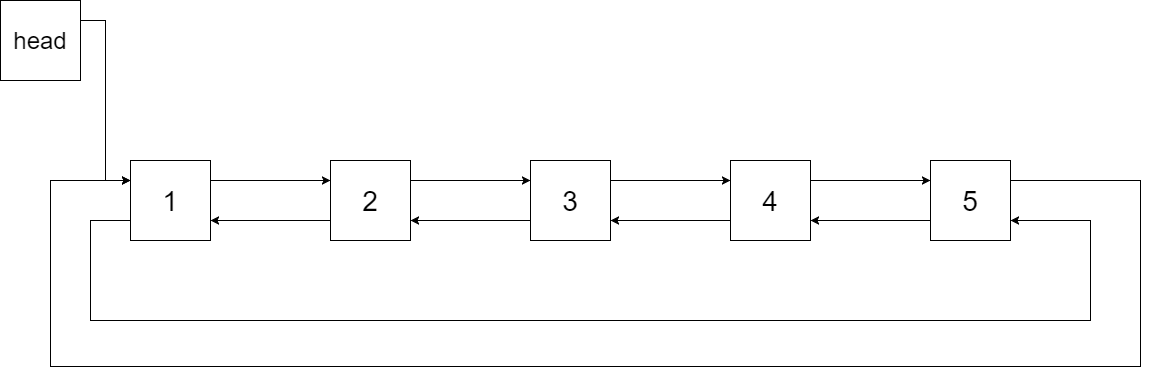
==输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表==。要求不能创建任何新的节点，只能调整树中节点指针的指向。为了让您更好地理解问题，以下面的二叉搜索树为例：

img

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

img

算法流程：

dfs(cur): 递归法中序遍历；

  • 终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
  • 递归左子树，即 dfs(cur.left) ；
  • 构建链表：
    • 当 pre 为空时： 代表正在访问链表头节点，记为 head ；
    • 当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ， cur.left = pre ；
    • 保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre ；
  • 递归右子树，即 dfs(cur.right) ；

treeToDoublyList(root)：

  • 特例处理： 若节点 root 为空，则直接返回；
  • 初始化： 空节点 pre ；
  • 转化为双向链表： 调用 dfs(root) ；
  • 构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可；
  • 返回值： 返回链表的头节点 head 即可；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        def dfs(cur):
            if not cur: 
              	return
            dfs(cur.left) # 递归左子树
            if self.pre: # 修改节点引用
                self.pre.right, cur.left = cur, self.pre
            else: # 记录头节点
                self.head = cur
            self.pre = cur # 保存 cur
            dfs(cur.right) # 递归右子树
        
        if not root: return
        self.pre = None
        dfs(root)
        self.head.left, self.pre.right = self.pre, self.head
        return self.head

给定一棵二叉搜索树，请找出其中第 k 大的节点的值。

  • 从大到小：倒序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        # 中序遍历是单调的
        def dfs(root):
            nonlocal k, res
            if not root: 
                return
            dfs(root.right)
            k -= 1
            if k == 0: 
                res = root.val
                return
            dfs(root.left)
        res = 0
        dfs(root)
        return res

    def kthLargest(self, root: TreeNode, k: int) -> int:
        if not root: return
        def TreeSize(root: TreeNode):# 求子树节点个数
          	# 子树的深度
            if not root: 
              	return 0
            if not root.left and not root.right: 
             		return 1
            return TreeSize(root.left) + TreeSize(root.right) + 1
        nright = TreeSize(root.right)
        if nright >= k: #在右子树
            return self.kthLargest(root.right, k)
        elif nright == k - 1: return root.val
        else: 
            return self.kthLargest(root.left, k - nright - 1)

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        queue, res = deque([root]), 0
        while queue:
            k = len(queue)
            for i in range(k):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right: 
                    queue.append(node.right)
            res += 1
        return res
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

[辅助函数]

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def height(root: TreeNode) -> int:
            if not root:
                return 0
            leftH = height(root.left)
            rightH = height(root.right)
            if leftH == -1 or rightH == -1 or abs(leftH - rightH) > 1:
                return -1
            else:
                return max(leftH, rightH) + 1
        return height(root) >= 0

求 1+2+...+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

1
2
3
4
5
class Solution:
    def sumNums(self, n: int) -> int:
        def sumStop(n):
            return n >= 1 and n + sumStop(n-1)
        return sumStop(n)

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

  • 若 root.val < p.val，则 pp 在 root 右子树 中；
  • 若 root.val > p.val ，则 pp 在 root 左子树 中；

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
      	# 迭代优化
        if p.val > q.val: p, q = q, p # 保证 p.val < q.val
        while root:
            if root.val < p.val: # p,q 都在 root 的右子树中
                root = root.right # 遍历至右子节点
            elif root.val > q.val: # p,q 都在 root 的左子树中
                root = root.left # 遍历至左子节点
            else: 
              	break
        return root
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
      	# 递归
        if root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        return root

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。深度优先遍历是从下往上返回，所以第一个满足的就是最近公共祖先节点 。

递归解析：
  • 终止条件：
    • 当越过叶节点，则直接返回 null；
    • 当 root等于 p, q ，则直接返回 root；
  • 递推工作：
    • 开启递归左子节点，返回值记为 left；
    • 开启递归右子节点，返回值记为 right ；
  • 返回值：根据 left 和 right ，可展开为四种情况；
    • 当 left 和 right 同时为空 ：说明 root的左 / 右子树中都不包含 p,q ，返回 null；
    • 当 left 和 right 同时不为空 ：说明 p, q分列在 root的 异侧 （分别在 左 / 右子树），因此 root为最近公共祖先，返回 root；
    • 当 left为空 ，right不为空 ：p,q都不在 root的左子树中，直接返回 right。具体可分为两种情况：
      • p,q 其中一个在 root的 右子树 中，此时 right 指向 p（假设为 p ）；
      • p,q 两节点都在 root的 右子树 中，此时的 right指向 最近公共祖先节点 ；
    • 当 left不为空 ， right为空 ：与情况 3. 同理；
1
2
3
4
5
6
7
8
9
class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root or root == q or root == p:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        return left if left else right

给定一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。计算从根节点到叶节点生成的 所有数字之和 。

  • 深度优先遍历、回溯【没有return】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def sumNumbers(self, root: TreeNode) -> int:
        # dfs , 回溯
        ans = []
        def dfs(root, prevTotal):
            if not root:
                return 0
            total = prevTotal * 10 + root.val
            if not root.left and not root.right:
                return total
            else:
                return dfs(root.left, total) + dfs(root.right, total)

        def backtrace(root, tmp):
            if not root:
                return root
            tmp.append(str(root.val))
            if not root.left and not root.right:
                ans.append(tmp[:])
                # 【没有return, 就会执行一次 pop() 】
            backtrace(root.left, tmp)
            backtrace(root.right, tmp)
            tmp.pop()
        backtrace(root, [])

        return sum([int("".join(nums)) for nums in ans])

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。节点 node 的子树为 node 本身，以及所有 node 的后代。

  • 建树【dfs 有返回值】
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def pruneTree(self, root: TreeNode) -> TreeNode:
        def dfs(root):
            if not root:
                return root
            root.left = dfs(root.left)
            root.right = dfs(root.right)
            if not root.left and not root.right and root.val == 0:
                return None
            return root    
        return dfs(root)

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

img

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3 解释：和等于 8 的路径有 3 条，如图所示。

  • 前缀和+回溯 o(n)、深度优先遍历【双重递归 0（n^2) 】

DFS中存在许多重复计算，我们定义节点的前缀和为：

  • curr 由根结点到当前结点的路径上所有节点的和；
  • 利用先序遍历二叉树，记录下根节点 root 到当前节点 p 的路径上除当前节点以外所有节点的前缀和；
  • 在已保存的路径前缀和中查找是否存在前缀和刚好等于当前节点到根节点的前缀和 curr 减去 targetSum。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        # 深度优先遍历
        def dfs(root, total):
            if not root:
                return 0
            ans = 0
            total += root.val
            if total == targetSum:
                ans += 1
            return ans + dfs(root.left, total) + dfs(root.right, total)
        if not root:
            return 0
        return dfs(root, 0) + self.pathSum(root.left, targetSum) + self.pathSum(root.right, targetSum)
    
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        # 前缀和 + 回溯
        pre = collections.defaultdict(int) # 根节点到当前节点和
        pre[0] = 1
        def backstace(root, curr):
            if not root:
                return 0
            curr += root.val # 根节点到当前节点和
            ans = 0
            ans += pre[curr - targetSum]
            # 回溯
            pre[curr] += 1
            ans += backstace(root.left, curr)
            ans += backstace(root.right, curr)
            pre[curr] -= 1
            return ans
        return backstace(root, 0)

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

给定一个二叉树的根节点 root ，返回其 最大路径和，即所有路径上节点值之和的最大值。

示例 2：

img

输入：root = [-10,9,20,null,null,15,7] 输出：42 解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

  • 节点贡献值 root + max(left, right) / 最大路径和：当前节点 + 左子树max + 右子树max
  • 动态过程保存：ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        ans = -inf
        def pathSum(root):
            nonlocal ans
            if not root:
                return 0
            left = max(pathSum(root.left), 0)
            right = max(pathSum(root.right), 0)
            if (t := root.val + left + right) > ans:
                ans = t
            return root.val + max(left, right)
        pathSum(root)
        return ans

给你一棵二叉搜索树，请 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。