贝叶斯分类器(4)EM算法
EM——期望最大 [概率模型]
EM 算法通过引入隐含变量,使用 MLE(极大似然估计)进行迭代求解参数。通常引入隐含变量后会有两个参数,EM 算法首先会固定其中的第一个参数,然后使用 MLE 计算第二个变量值;接着通过固定第二个变量,再使用 MLE 估测第一个变量值,依次迭代,直至收敛到局部最优解。
EM 算法,全称 Expectation Maximization Algorithm。期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最大似然估计或极大后验概率估计。
本文思路大致如下:先简要介绍其思想,然后举两个例子帮助大家理解,有了感性的认识后再进行严格的数学公式推导。
1. 思想
EM 算法的核心思想非常简单,分为两步:Expection-Step 和 Maximization-Step。E-Step 主要通过观察数据和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望值;而 M-Step 是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加,所以函数最终会收敛。
\(E M\) 算法一句话总结就是: \(E\) 步固定 \(\theta\) 优化 \(Q, M\) 步固定 \(Q\) 优化 \(\theta\) 。
2 例子
2.1 例子 A
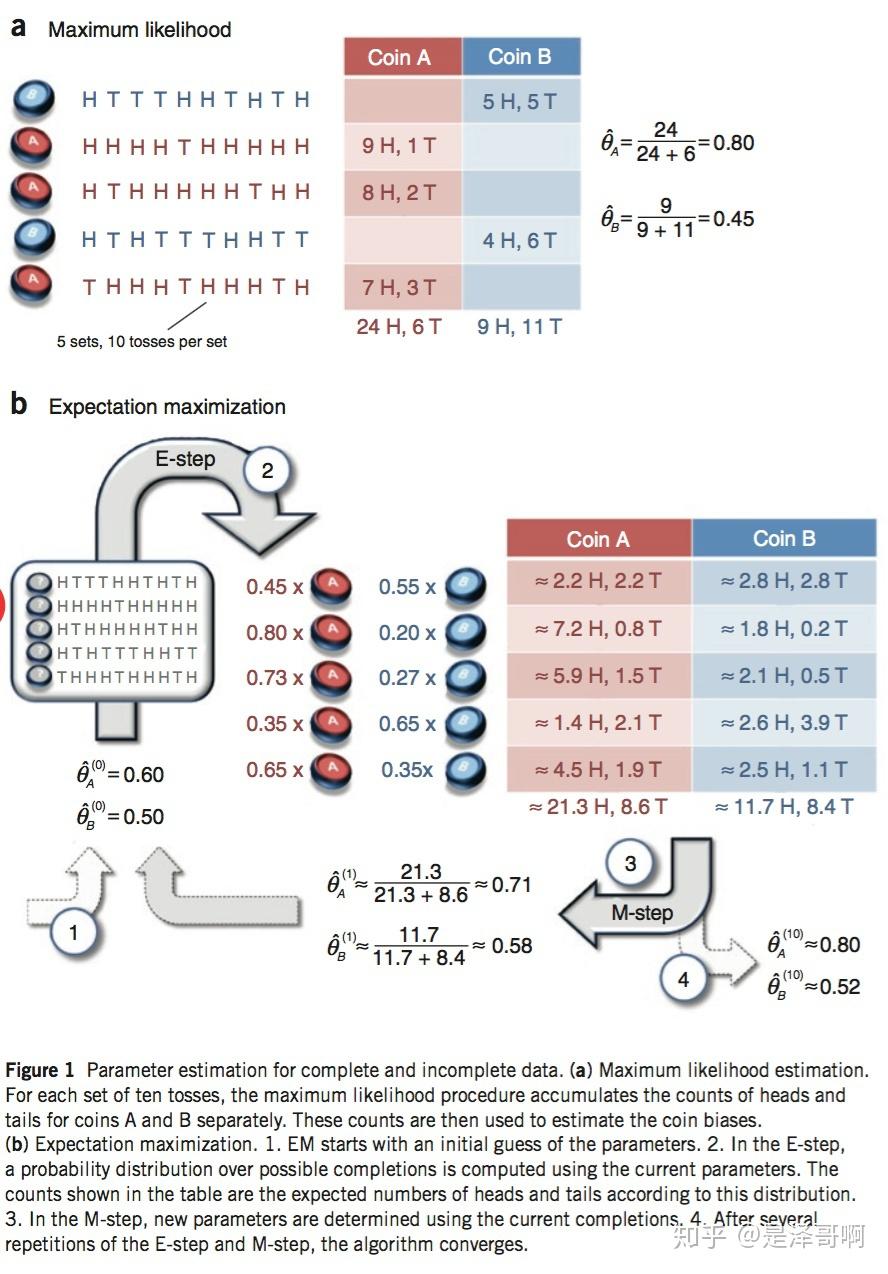
假设有两枚硬币 \(\mathrm{A}\) 和 \(B\), 他们的随机抛郑的结果如下图所示:
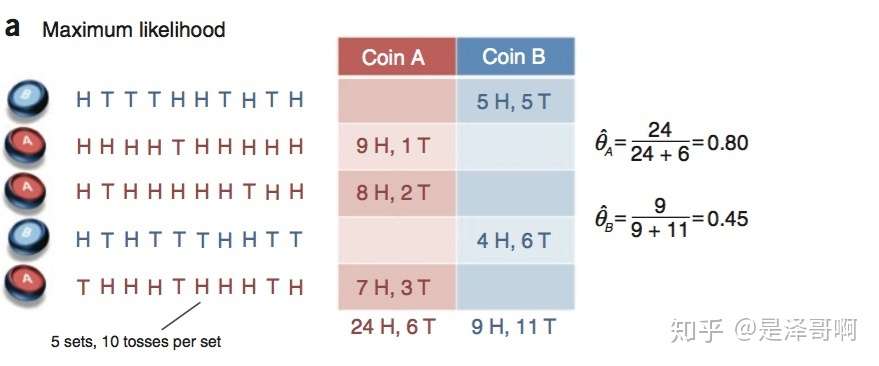
我们很容易估计出两枚硬币抛出正面的概率: \[ \begin{aligned} & \theta_A=24 / 30=0.8 \\ & \theta_B=9 / 20=0.45 \end{aligned} \] 现在我们加入隐变量, 抺去每轮投郑的硬币标记:
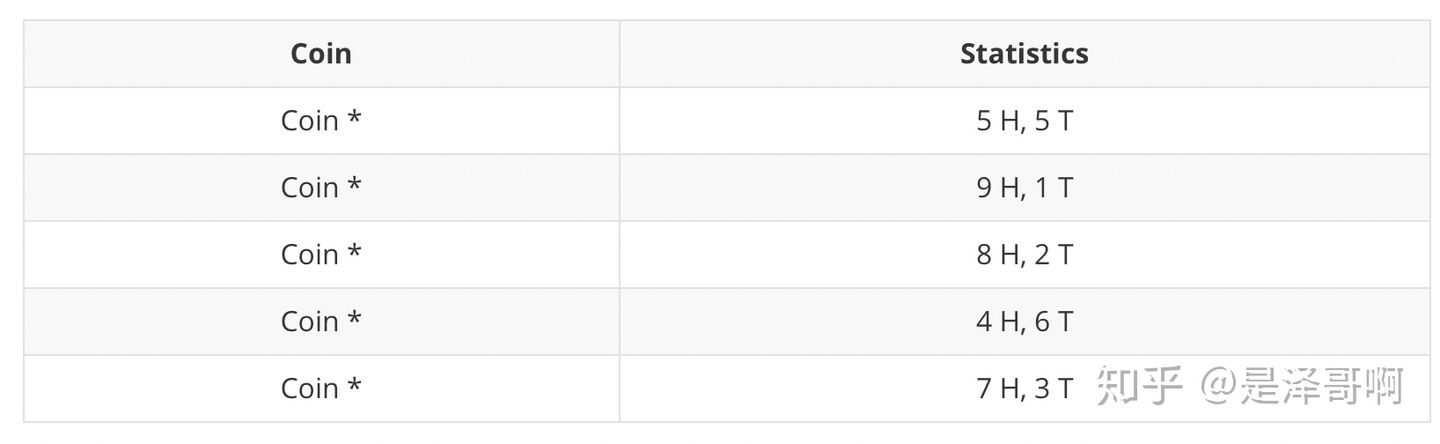
碰到这种情况, 我们该如何估计 \(\theta_A\) 和 \(\theta_B\) 的值?
我们多了一个隐变量 \(Z=\left(z_1, z_2, z_3, z_4, z_5\right)\), 代表每一轮所使用的硬币, 我们需要知道每一轮抛郑所使用的硬币这样才能估计 \(\theta_A\) 和 \(\theta_B\) 的值, 但是估计隐变量 \(\mathrm{Z}\) 我们又需要知道 \(\theta_A\) 和 \(\theta_B\) 的值, 才能用极大似然估计法去估计出 Z。这就陷入了一个鸡生蛋和蛋生鸡的问题。
其解决方法就是先随机初始化 \(\theta_A\) 和 \(\theta_B\), 然后用去估计 \(Z\), 然后基于 \(Z\) 按照最大似然概率去估计新的 \(\theta_A\) 和 \(\theta_B\) , 循环至收敛。
2.1.2 计算
随机初始化 \(\theta_A=0.6\) 和 \(\theta_B=0.5\)
对于第一轮来说, 如果是硬币 \(A\),
得出的 5 正 5 反的概率为: \(0.6^5 *
0.4^5\); 如果是硬币 \(B\),
得出的 5 正 5 反的概率为: \(0.5^5 *
0.5^5\) 。我们可以算出使用是硬币 \(A\) 和硬币 \(B\) 的概率 分别为: \[
\begin{aligned}
& P_A=\frac{0.6^5 * 0.4^5}{\left(0.6^5 * 0.4^5\right)+\left(0.5^5 *
0.5^5\right)}=0.45 \\
& P_B=\frac{0.5^5 * 0.5^5}{\left(0.6^5 * 0.4^5\right)+\left(0.5^5 *
0.5^5\right)}=0.55
\end{aligned}
\] 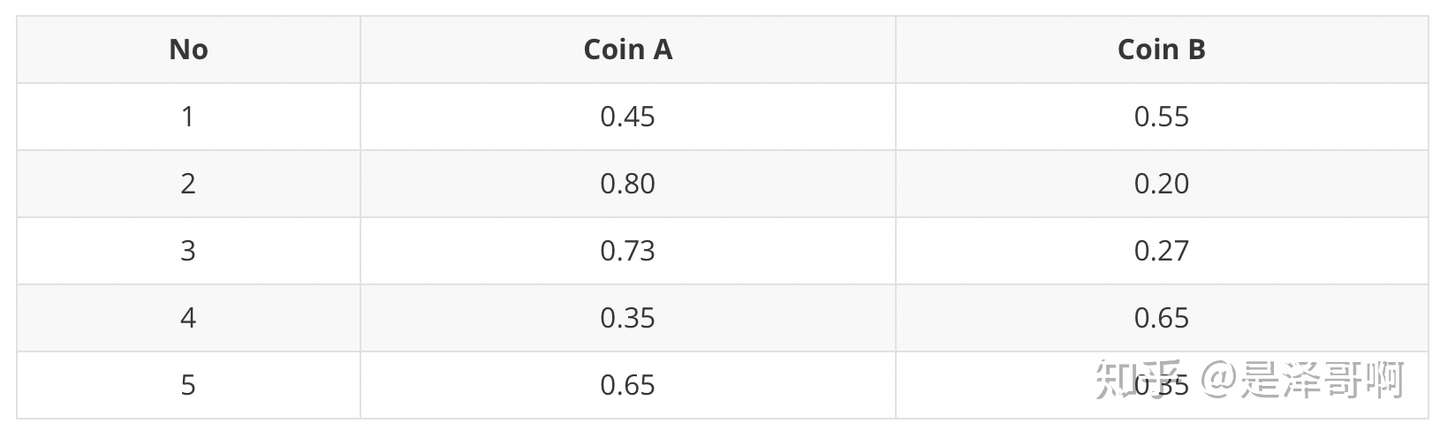
从期望的角度来看, 对于第一轮抛郑, 使用硬币 \(A\) 的概率是 0.45 , 使用硬币 \(B\) 的概率是 0.55。同理其他轮。这一 步我们实际上是估计出了 Z 的概率分布,这部就是 E-Step。
结合硬币 \(A\) 的概率和上一张结果, 我们利用期望可以求出硬币 \(A\) 和硬币 \(B\) 的贡献。以第二轮硬币 \(A\) 为例子, 计算方式为: \[ \begin{aligned} & H: 0.80 * 9=7.2 \\ & T: 0.80 * 1=0.8 \end{aligned} \] 于是我们可以得到:
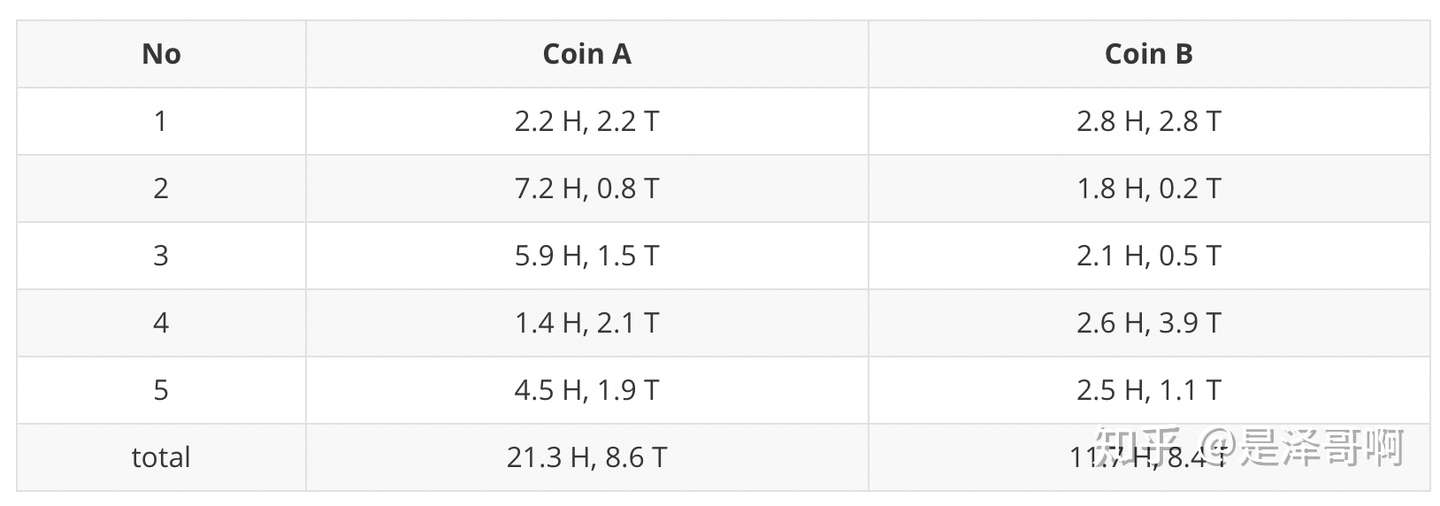
然后用极大似然估计来估计新的 \(\theta_A\) 和 \(\theta_B\) 。 \[ \begin{aligned} \theta_A & =\frac{21.3}{21.3+8.6}=0.71 \\ \theta_B & =\frac{11.7}{11.7+8.4}=0.58 \end{aligned} \]
这步就对应了 M-Step,重新估计出了参数值。如此反复迭代,我们就可以算出最终的参数值。
上述讲解对应下图:
2.2 例子 B
如果说例子 A 需要计算你可能没那么直观, 那就举更一个简单的例子:
现在一个班里有 50 个男生和 50 个女生,且男女生分开。我们假定男生的身高服从正态分布: \(N\left(\mu_1, \sigma_1^2\right)\) , 女生的身高则服从另一个正态分布: \(N\left(\mu_2, \sigma_2^2\right)\) 。这时候我们可以用 极大似然法 (MLE) , 分别通过这 50 个男生和 50 个女生的样本来估计这两个正态分布的参数。
但现在我们让情况复杂一点, 就是这 50 个男生和 50 个女生混在一起了。我们拥有 100 个人的身高数据, 却不知 道这 100 个人每一个是男生还是女生。
这时候情况就有点箩尬, 因为通常来说, 我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更 有可能是男生还是女生。但从另一方面去考量, 我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女 各自身高的正态分布的参数。
这个时候有人就想到我们必须从某一点开始, 并用迭代的办法去解决这个问题:我们先设定男生身高和女生身高分 布的几个参数(初始值), 然后根据这些参数去判断每一个样本 (人)是男生还是女生, 之后根据标注后的样本再 反过来重新估计参数。之后再多次重复这个过程,直至稳定。这个算法也就是 EM 算法。
3. 推导
给定数据集, 假设样本间相互独立, 我们想要拟合模型 \(p(x ; \theta)\) 到数据的参数。根据分布我们可以 得到如下似然函数: \[ \begin{aligned} L(\theta) & =\sum_{i=1}^n \log p\left(x_i ; \theta\right) \\ & =\sum_{i=1}^n \log \sum_z p\left(x_i, z ; \theta\right) \end{aligned} \]
第一步是对极大似然函数取对数,第二步是对每个样本的每个可能的类别 z 求联合概率分布之和。如果这个 z 是已知的数,那么使用极大似然法会很容易。但如果 z 是隐变量,我们就需要用 EM 算法来求。事实上,隐变量估计问题也可以通过梯度下降等优化算法,但事实由于求和项将随着隐变量的数目以指数级上升,会给梯度计算带来麻烦;而 EM 算法则可看作一种非梯度优化方法。
3.1 求解含有隐变量的概率模型
为了求解含有隐变量 \(z\) 的概率模型 \(\hat{\theta}=\underset{\theta}{\arg \max } \sum_{i=1}^m \log \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)\) 需要一些特殊的技巧, 通过引入隐变量\(z^{(i)}\) 的概率分布为 \(Q_i\left(z^{(i)}\right)\), 因为 \(\log (x)\) 是凹函数故结合凹函数形式下的詹森不等式进行放缩处理 \[ \begin{aligned} \sum_{i=1}^m \log \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right) & =\sum_{i=1}^m \log \sum_{z^{(i)}} Q_i\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)} \\ & =\sum_{i=1}^m \log \mathbb{E}\left(\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)}\right) \\ & \left.\geq \sum_{i=1}^m \mathbb{E}\left[\log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)}\right)\right] \\ & =\sum_{i=1}^m \sum_{z^{(i)}} Q_i\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)} \end{aligned} \] 其中由概率分布的充要条件 \(\sum_{z^{(i)}} Q_i\left(z^{(i)}\right)=1 、 Q_i\left(z^{(i)}\right) \geq 0\) 可看成下述关于 \(z\) 函数分布列的形式:

这个过程可以看作是对 \(\mathcal{L}(\theta)\) 求了下界, 假设 \(\theta\) 已经给定那么 \(\mathcal{L}(\theta)\) 的值就取决于 \(Q_i\left(z^{(i)}\right)\) 和 \(p\left(x^{(i)}, z^{(i)}\right)\) 了, 因 此可以通过调整这两个概率使下界不断上升, 以逼近 \(\mathcal{L}(\theta)\) 的真实值, 当不等式变成等式时说明调整后的概率能够 等价于 \(\mathcal{L}(\theta)\) ,所以必须找到使得等式成立的条件, 即寻找 \[ \left.\mathbb{E}\left[\log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)}\right)\right]=\log \mathbb{E}\left[\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)}\right] \] 由期望得性质可知当 \[ \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)}=C, \quad C \in \mathbb{R} \quad(*) \] 等式成立,对上述等式进行变形处理可得 \[ \begin{aligned} & p\left(x^{(i)}, z^{(i)} ; \theta\right)=C Q_i\left(z^{(i)}\right) \\ & \Leftrightarrow \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)=C \sum_{z^{(i)}} Q_i\left(z^{(i)}\right)=C \\ & \Leftrightarrow \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)=C \end{aligned} \] 把 \((* *)\) 式带入 \((*)\) 化简可知 \[ \begin{aligned} Q_i\left(z^{(i)}\right) & =\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{\sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)} \\ & =\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{p\left(x^{(i)} ; \theta\right)} \\ & =p\left(z^{(i)} \mid x^{(i)} ; \theta\right) \end{aligned} \] 至此, 可以推出在固定参数 \(\theta\) 后, \(Q_i\left(z^{(i)}\right)\) 的计算公式就是后验概率, 解决了 \(Q_i\left(z^{(i)}\right)\) 如何选择得问题。这一步 称为 \(E\) 步, 建立 \(\mathcal{L}(\theta)\) 得下界; 接下来得 \(M\) 步, 就是在给定 \(Q_i\left(z^{(i)}\right)\) 后, 调整 \(\theta\) 去极大化 \(\mathcal{L}(\theta)\) 的下界即 \[ \begin{aligned} & \underset{\theta}{\arg \max } \sum_{i=1}^m \log p\left(x^{(i)} ; \theta\right) \\ & \Leftrightarrow \underset{\theta}{\arg \max } \sum_{i=1}^m \sum_{z^{(i)}} Q_i\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_i\left(z^{(i)}\right)} \\ & \Leftrightarrow \underset{\theta}{\arg \max } \sum_{i=1}^m \sum_{z^{(i)}} Q_i\left(z^{(i)}\right)\left[\log p\left(x^{(i)}, z^{(i)} ; \theta\right)-\log Q_i\left(z^{(i)}\right)\right] \\ & \Leftrightarrow \underset{\theta}{\arg \max } \sum_{i=1}^m \sum_{z^{(i)}} Q_i\left(z^{(i)}\right) \log p\left(x^{(i)}, z^{(i)} ; \theta\right) \end{aligned} \] 因此EM算法的迭代形式为:

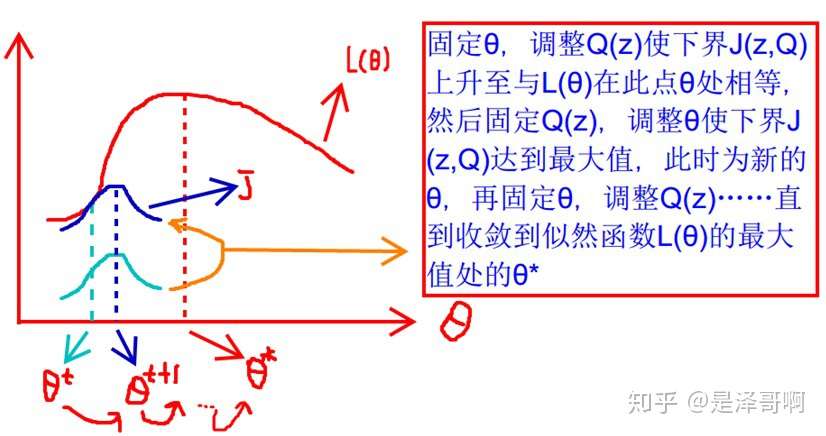
这张图的意思就是: 首先我们固定 \(\theta\), 调整 \(Q(z)\) 使下界 \(J(z, Q)\) 上升至与 \(L(\theta)\) 在此点 \(\theta\) 处相等 (绿色曲线到 蓝色曲线) , 然后固定 \(Q(z)\), 调整 \(\theta\) 使下界 \(J(z, Q)\) 达到最大值 \(\left(\theta_t\right.\) 到 \(\left.\theta_{t+1}\right)\) ,然后再固定 \(\theta\), 调整 \(Q(z)\) , 一直到收敛到似然函数 \(L(\theta)\) 的最大值处的 \(\theta\) 。
EM 算法通过引入隐含变量,使用 MLE(极大似然估计)进行迭代求解参数。通常引入隐含变量后会有两个参数,EM 算法首先会固定其中的第一个参数,然后使用 MLE 计算第二个变量值;接着通过固定第二个变量,再使用 MLE 估测第一个变量值,依次迭代,直至收敛到局部最优解。
3.2 EM算法的收敛性
不妨假设 \(\theta^{(k)}\) 和 \(\theta^{(k+1)}\) 是EM算法第 \(k\) 次迭代和第 \(k+1\) 次迭代的结果, 要确保 \(E M\) 算法收敛那么等价于证明 \(\mathcal{L}\left(\theta^{(k)}\right) \leq \mathcal{L}\left(\theta^{(k+1)}\right)\) 也就是说极大似然估计单调增加, 那么算法最终会迭代到极大似然估计的最大值。在选定 \(\theta^{(k)}\) 后可以得到 \(E\) 步 \(Q_i^{(k)}\left(z^{(i)}\right)=p\left(z^{(i)} \mid x^{(i)} ; \theta^{(k)}\right)\), 这一步保证了在给定 \(\theta^{(k)}\) 时, 詹森不等式中的等式成立即 \(\mathcal{L}\left(\theta^{(k)}\right)=\sum_{i=1}^m \sum_{z^{(i)}} Q_i^{(k)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(k)}\right)}{Q_i\left(z^{(i)}\right)}\)
然后再进行 \(M\) 步, 固定 \(Q_i^{(k)}\left(z^{(i)}\right)\) 并将 \(\theta^{(k)}\) 视作变量, 对上式 \(\mathcal{L}\left(\theta^{(k)}\right)\) 求导后得到 \(\theta^{(k+1)}\) 因此有如下式子成立 \[ \begin{aligned} \mathcal{L}\left(\theta^{(k)}\right) & =\sum_{i=1}^m \sum_{z^{(i)}} Q_i^{(k)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(k)}\right)}{Q_i\left(z^{(i)}\right)} \\ & \leq \sum_{i=1}^m \sum_{z^{(i)}} Q_i^{(k)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(k)}\right)}{Q_i\left(z^{(i)}\right)} \\ & \leq \mathcal{L}\left(\theta^{(k+1)}\right) \end{aligned} \] 首先 (a) 式是前面 \(E\) 步所保证詹森不等式中的等式成立的条件, (a) 到 (b) 是 \(M\) 步的定义, (b) 到 (c) 对任意 参数都成立, 而其等式的条件是固定 \(\theta\) 并调整好 \(Q\) 时成立, \((b)\) 到 \((c)\) 只是固定 \(Q\) 调整 \(\theta\), 在得到 \(\theta^{(k+1)}\) 时, 只是最大化 \(\mathcal{L}\left(\theta^{(k)}\right)\), 也就是 \(\mathcal{L}\left(\theta^{(k+1)}\right)\) 的一个下界而没有使等式成立。
4. 另一种理解
坐标上升法(Coordinate ascent):

途中直线为迭代优化路径,因为每次只优化一个变量,所以可以看到它没走一步都是平行与坐标轴的。
EM 算法类似于坐标上升法,E 步:固定参数,优化 Q;M 步:固定 Q,优化参数。交替将极值推向最大。
5. 应用
EM 的应用有很多,比如、混合高斯模型、聚类、HMM 等等。其中 EM 在 K-means 中的用处,我将在介绍 K-means 中的给出。