风控算法（3）技术算法-评分卡基础

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 3k 阅读时长 ≈ 5 分钟

评分卡基础—逻辑回归算法理解

风控业务背景

逻辑回归（Logistic Regression，LR）是建立信贷金融评分卡的重要模型，其具有形式简单、易于解释、鲁棒性强等优点。然而，很多建模同学并不是很清楚其原理。本文尝试对逻辑回归基础加以分析理解。

目录 Part 1. 从线性回归到逻辑回归 Part 2. 为什么采用sigmoid函数 Part 3. 利用极大似然估计法估计参数 Part 4. 最优化问题求解之梯度下降法 Part 5. 正则项的作用和种类 Part 6. 总结 致谢 版权声明 参考资料

一、从线性回归到逻辑回归

线性模型是指对各种属性进行线性加权组合的函数：

[公式]

这一过程将信息进行整合；不同的权重(weight)反映了自变量对因变量不同的贡献程度 。线性回归（Liner Regression）具有广泛应用，例如：预测房价、天气等等。

但在实际应用中，很多人会忽略线性回归的几大假设：

  • 零均值假设：随机误差项均值为0。
  • 同方差假设：随机误差项方差相同。若满足这一特性，称模型具有同方差性
  • 残差 [公式] 服从正态分布 [公式]
  • 无自相关假设：若不满足这一特性，称模型具有自相关性（Autocorrelation）。
  • ...

显然，线性回归的输出结果 [公式] 。那如果要做分类呢？我们就考虑将线性回归的输出与分类任务的真实标签 [公式]联系起来，即再找一个映射函数。

我们采用一个 [公式] 函数（也叫对数几率）：

[公式]

其函数图像如图2所示，直观感受其优美的姿态，对称、平滑，且输出 [公式] .

img

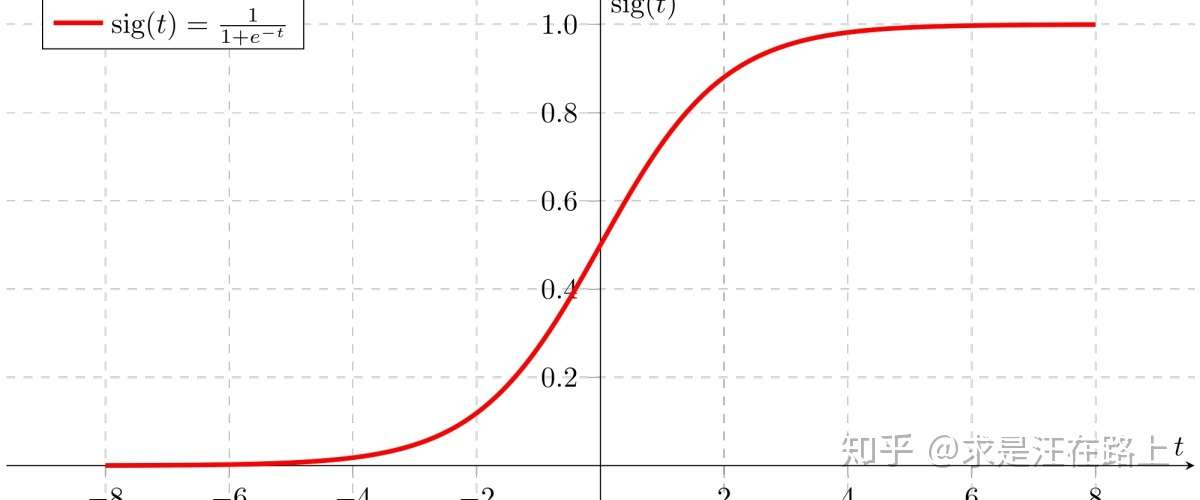
我们尝试把 [公式] 函数模块拼接到线性回归的输出后面，如图3所示。

img

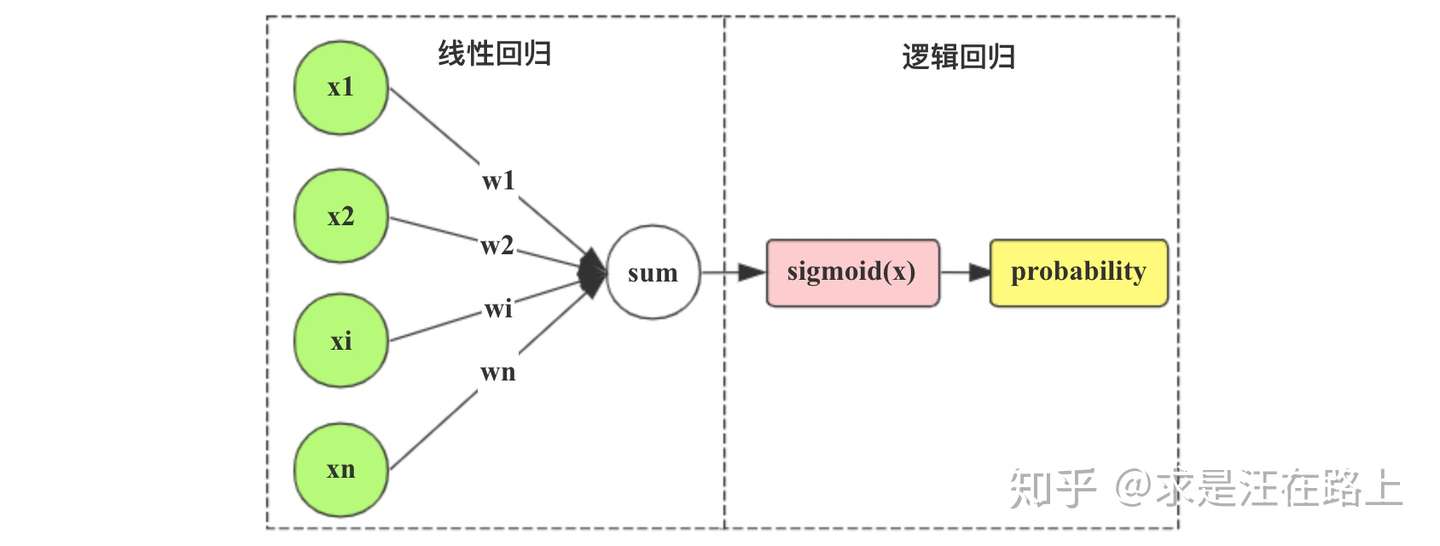
把图3用公式表达，也就是在 [公式] 函数内嵌套一个线性回归：

[公式]

我们再将其变换得到逻辑回归的另一种常见形式：

[公式]

为什么要这样做呢？这是因为右边就是线性回归，而左边则引入了 [公式] (几率) 的概念，即事件发生概率相对于不发生概率的比值。

显然可以得到正负样例的概率表达式：

[公式]

二、为什么采用sigmoid函数

根本原因：

函数优点：

至此，你可能会有疑问：为什么这里就直接选择了[公式] 函数？如果只是为了将输出结果从 [公式] 映射到 [公式] ，完全可以选择其他函数，比如单位阶跃函数：

[公式]

若预测值 [公式] 则判为正例， [公式] 则判为负例， [公式] 则可任意判别。你可能会说，这个阶跃函数不可微，也无法像[公式] 函数那样输出概率。这就冒出两个问题：

  1. 为什么这个映射函数一定要求可微？
  2. 为什么 [公式] 函数输出值可以代表概率？

首先，我们先分析 [公式] 函数的基本性质：

  1. 定义域：[公式]
  2. 值域：[公式]
  3. 函数在定义域内为连续和光滑函数
  4. 处处可导，导数为 [公式] ，以下是推导过程：
[公式]

可以看到，[公式] 函数确实具有很多优点，但这仍不是我们选择它的根本原因。这是因为，我们仍可以找到一些与之类似性质的函数。

根本原因：

由于逻辑回归本质上属于线性模型，我们尝试从广义线性模型（Generalized Linear Model，GLM）角度入手解释。前文提到，线性回归存在诸多假设，实际应用中往往无法满足。这就会有以下问题：

  • [公式] 的取值范围 [公式] 与某些场景矛盾。例如，要求 [公式] 。假设一个线性回归模型预测当温度下降10摄氏度，沙滩上的游客将减少1000人。那么，如果当前20摄氏度时，沙滩上只有50人，按此模型预测，当温度为10摄氏度时，沙滩上便有-950人。这显然不符合常理，因为人数不能为负数。
  • 残差 [公式] 服从正态分布 [公式] ，且要求方差 [公式] 是常数。但有时，均值 [公式] 越大，我们越预测不准确（方差 [公式] 越大）。

为了解决这些局限性，后人发展了GLM，用以提高线性模型的普适性。

GLM允许因变量 \(y\) 的分布并不一定要服从正态分布，而可以服从其它分布。

广义线性模型GLM由三要素组成, 即：

  • 概率分布 (Probability distribution) : 指因变量 \(y\) 的分布假设, 来自指数分布族。

  • 线性预测 (Linear predictor) : 自变量的线性组合, 即 \(\eta=\boldsymbol{X} \boldsymbol{\beta}\)

  • 链接函数 (Link function) : 通过均值 \(\mu\) 来链接前两者, 即 \(E(Y)=\mu=g^{-1}(\eta)\) image-20220708133222814

    首先分析概率分布。对于只有单个参数 \(\theta\) 的指数分布族的通用形式为: \[ f(x \mid \theta)=h(x) \exp (\eta(\theta) \cdot T(x)-A(\theta)) \] 其中, \(h(x)\) 和 \(T(x)\) 只是关于自变量 \(x\) 的函数； \(\eta(\theta)\) 和 \(A(\theta)\) 只是关于末知参数 \(\theta\) 的函数。 不同的线性模型具有不同的分布假设。比如：

  • 线性回归假设 \(y\) 的残差 \(\varepsilon\) 服从正态分布 \(N\left(\mu, \sigma^{2}\right)\)

  • 逻辑回归假设 \(y\) 服从伯努利分布 (Bernoulli)

接下来，我们尝试：

  1. 将逻辑回归因变量 \(y\) 变换到式 [公式] 的形式，确定以上几个函数，验证其属于指数分布族。
  2. 求解出逻辑回归对应的链接函数。注意，此时我们还没有认可sigmoid函数。⚠️

由于逻辑回归假设 \(y\) 服从伯努利分布（Bernoulli），即：

[公式]

对比式 [公式] 指数函数族的通用形式，我们发现：

  • [公式]
  • [公式]

这说明伯努利分布也是指数分布族（exponential family）的成员。按GLM的第二要素定义：

[公式]

我们再计算 [公式] 的反函数，就得到了[公式] 函数：

[公式]

按类似方法，我们可以推导出各分布函数及其链接函数，如图5所示。

img

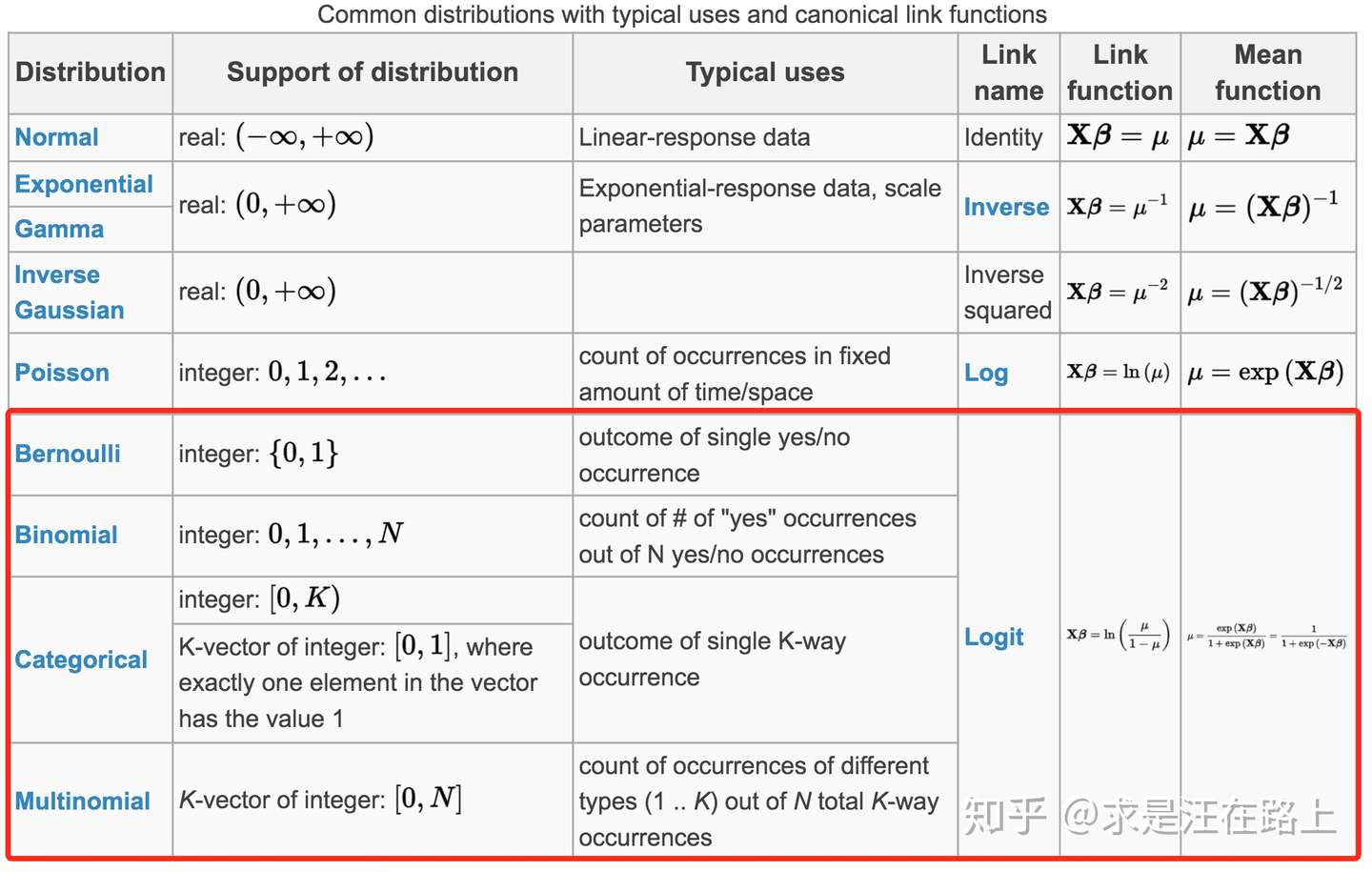
从广义线性模型角度，我们确实推导出 [公式]函数与逻辑回归之间密不可分的联系。但是，sigmoid函数输出值为什么可以代表概率？

上文提到，逻辑回归中因变量 \(y\) 服从伯努利分布，而伯努利分布的参数 [公式] 的含义就是样例属于 [公式] 的概率。

三、利用极大似然估计法估计参数

在模型参数估计问题上，两大主流学派持有不同观点：

  • 频率主义学派（Frequentist）： 认为参数虽然未知，但却是客观存在的固定值。因此，可通过优化似然函数等准则估计参数值。
  • 贝叶斯学派（Bayesian）： 认为参数是未观察到的随机变量，其本身也可有分布。因此，可假定参数服从一个先验分布，再基于观察到的数据来计算参数的后验分布。

极大似然估计法（Maximum Likelihood Estimation，MLE）属于频率主义学派方法，其蕴含的朴素思想在于：

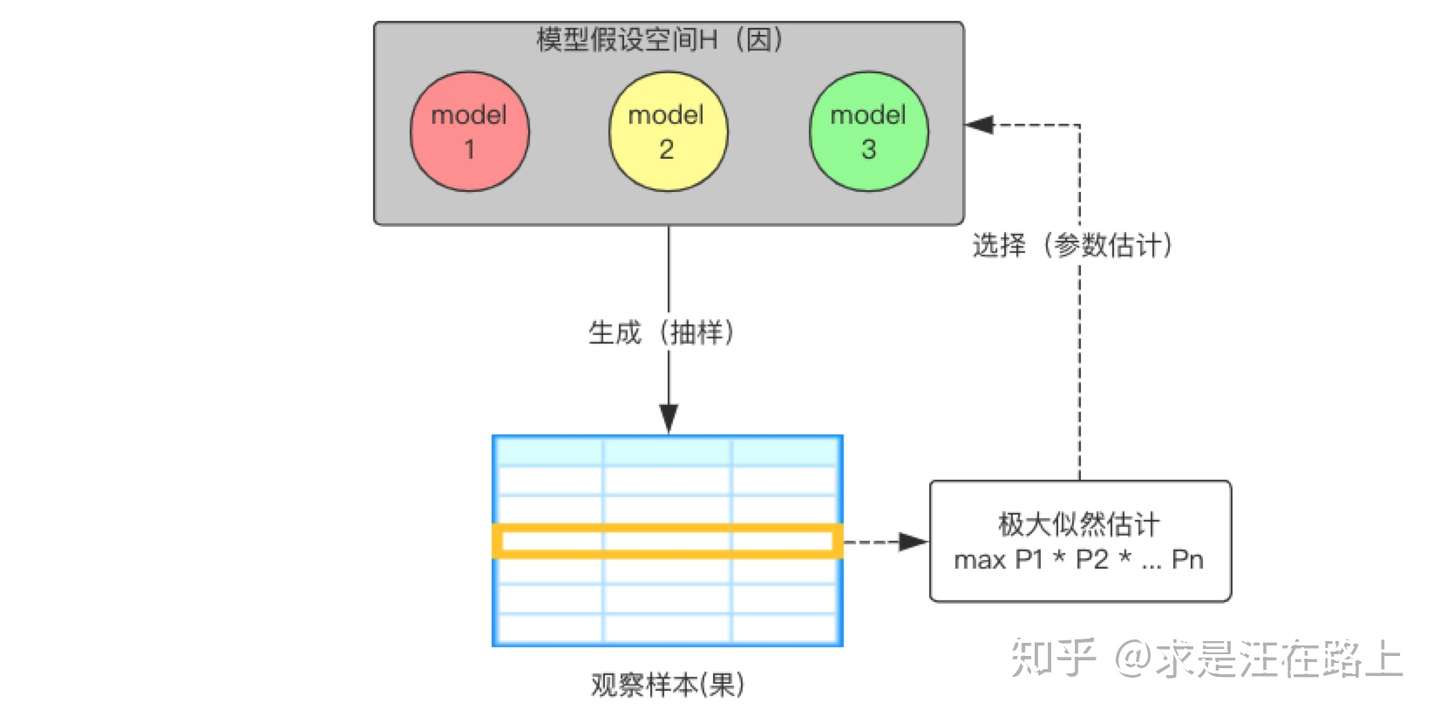
我们已经确定了一个模型种类 [公式] ，但还不清楚其真实参数 [公式] 。既然目前观察样本已经出现，那么就由果溯因，估计出一组参数 [公式] ，使得出现目前结果的可能性最大（优化目标)，如图6所示。

由于一组样本中的所有样例是一个整体，因此我们将各样例的概率相乘（排列组合中的乘法原理）来得到我们的目标函数。

img

我们把第 [公式] 个样例的类别属于 [公式] 的概率记为： [公式] .

现在，我们有观测样本 [公式] ，那么似然函数为：

[公式]

其中，样例 [公式] 具有标签 [公式] 。右边为什么要写成这种形式呢？主要原因在于这是伯努利分布的常见形式。按正负样例分析，可以帮助你理解这个形式：

  • [公式] 时，[公式]
  • [公式] 时，[公式]

为便于求解，将连乘 [公式] 转为 [公式] ，我们对等式 [公式] 两边同取对数 [公式] ，写成对数似然函数：

[公式]

我们的优化目标是：

[公式]

认真考虑后，我们发现并没有其他约束项。(事实上，这里将蕴含正则项的思想)

四、最优化问题求解之梯度下降法

回到式 [公式] 这个问题中：

[公式]

我们不断重复这一过程：达到某个点 [公式] 后，继续计算下一个点 [公式] ：

[公式]

那么，这个迭代过程何时才能停止呢？一般满足以下任意条件即可：

  • 达到迭代次数上限： [公式]
  • 学习曲线变化很小：[公式] 小于阈值。