理论基础（3）参数估计

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 2.6k 阅读时长 ≈ 5 分钟

机器学习优化方法 (Optimization)

机器学习与优化基础（Machine Learning and Optimization）:https://zhuanlan.zhihu.com/p/169835477

最优化方法复习笔记：https://github.com/LSTM-Kirigaya/OptimizeNote

FreeWill：机器学习算法系列（25）：最速下降法、牛顿法、拟牛顿法

一、什么是凸优化

凸函数的严格定义为, 函数 \(L(\cdot)\) 是凸函数当且仅当对定义域中的任意两点 \(x, y\) 和任意实数 \(\lambda \in[0,1]\) 总有: \[ L(\lambda x+(1-\lambda) y) \leq \lambda L(x)+(1-\lambda) L(y) \] 该不等式的一个直观解释是, 凸函数曲面上任意两点连接而成的线段, 其上的任 意一点都不会处于该函数曲面的 下方，如下图所示所示。

该不等式的一个直观解释是，凸函数曲面上任意两点连接而成的线段，其上的任 意一点都不会处于该函数曲面的下方，如下图所示所示。

img

凸优化问题的例子包括支持向量机、线性回归等 线性模型，非凸优化问题的例子包括低秩模型（如矩阵分解）、深度神经网络模型等。

二、正则化项

使用正则化项，也就是给loss function加上一个参数项，正则化项有L1正则化、L2正则化、ElasticNet。加入这个正则化项好处：

  • 控制参数幅度，不让模型“无法无天”。
  • 限制参数搜索空间
  • 解决欠拟合与过拟合的问题。

三、常见的几种最优化方法

下面以线性模型损失函数为例：

3.1 梯度下降法

梯度下降法是最早最简单，也是最为常用的最优化方法。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。 \[ \begin{gathered}\frac{\partial}{\partial \theta_j} J(\theta)=\frac{\partial}{\partial \theta_j} \frac{1}{2}\left(h_\theta(x)-y\right)^2 \\ =2 \cdot \frac{1}{2}\left(h_\theta(x)-y\right) \frac{\partial}{\partial \theta_j}\left(h_\theta(x)-y\right) \\ =\left(h_\theta(x)-y\right) x_j\end{gathered} \] 梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。梯度下降法的搜索迭代示意图如下图所示：

img

  • 批量梯度下降法（BGD）

参数θ的值每更新一次都要遍历样本集中的所有的样本，得到新的θj，看是否满足阈值要求，若满足，则迭代结束，根据此值就可以得到；否则继续迭代。【易受极小值影响】

  • 随机梯度下降算法（SGD）【单样本增量梯度下降】

每次更新只用到一个训练样本，若根据当前严格不能进行迭代得到一个，此时会得到一个，有新样本进来之后，在此基础上继续迭代，又得到一组新的和，以此类推。

缺点：靠近极小值时收敛速度减慢；直线搜索时可能会产生一些问题；可能会“之字形”地下降。

3.2 牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数 \(\mathrm{f}(\mathrm{x})\) 的泰勒级数的前面几项来寻找方程 \((x)=0\) 的根。牛顿法最大的特点就在于它的收敛速度很快。具体步骤：

  • 首先, 选择一个接近函数 \(f(x)\) 零点的 \(x 0\), 计算相应的 \(f(x 0)\) 和切线斜率 \(f^{\prime}(x 0)\) (这里 \(f^{\prime}\) 表示函数 \(f\) 的导 数)
  • 然后我们计算穿过点 \((x 0, f(x 0))\) 并且斜率为 \(f^{\prime}(x 0)\) 的直线和 \(x\) 轴的交点的 \(x\) 坐标, 也就是求如下方程的解: \(x * f^{\prime}\left(x_0\right)+f\left(x_0\right)-x_0 * f^{\prime}\left(x_0\right)=0\)
  • 我们将新求得的点的 \(x\) 坐标命名为 \(x 1\), 通常 \(x 1\) 会比 \(x 0\) 更接近方程 \(f(x)=0\) 的解。因此我们现在可以利用 \(x 1\) 开始下一轮迭代。

由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是"切线法"。牛顿法搜索动态示例图：

img

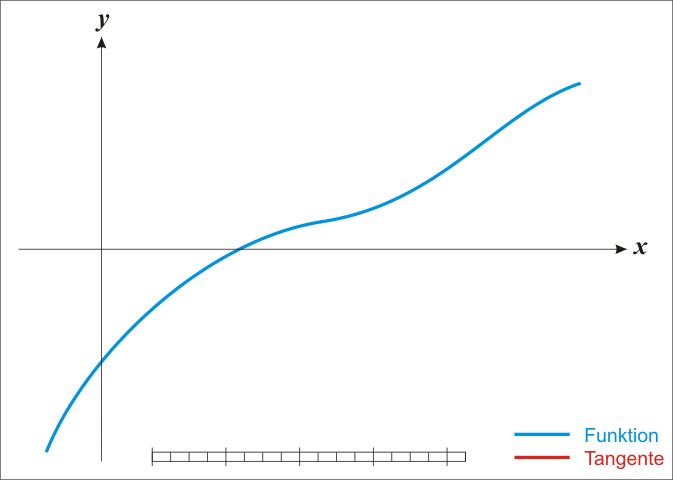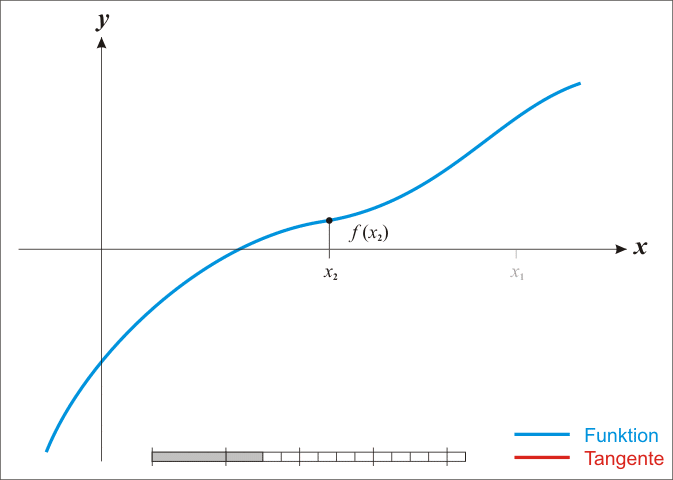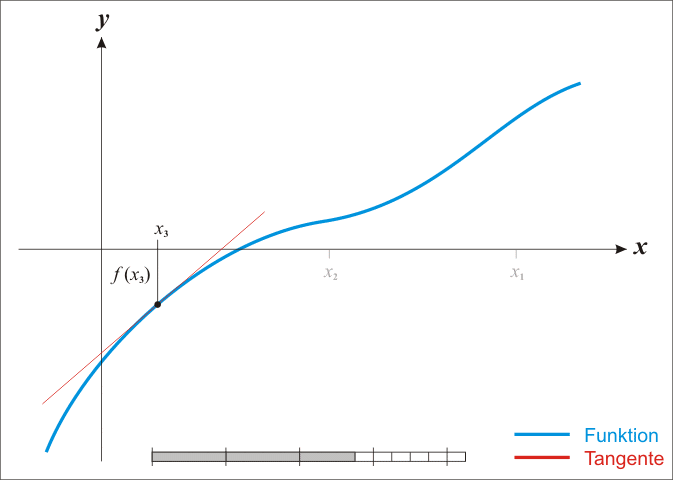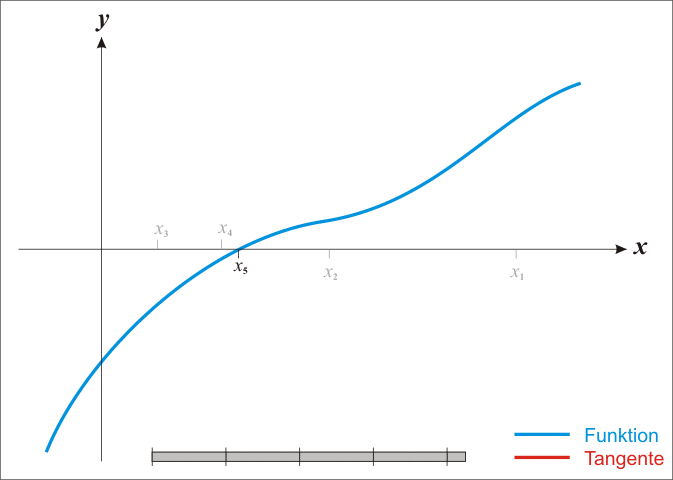
从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。缺点：

  • 牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。
    • 在高维情况下这个矩阵非常大，计算和存储都是问题。
  • 在小批量的情况下，牛顿法对于二阶导数的估计噪声太大。
    • 目标函数非凸的时候，牛顿法容易受到鞍点或者最大值点的吸引。

3.3 拟牛顿法

拟牛顿法是求解非线性优化问题最有效的方法之一，本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。拟牛顿法和梯度下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于梯度下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

DFP、BFGS、L-BFGS:

image-20220509171547743

3.4 共轭梯度法

共轭梯度法是介于梯度下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了梯度下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。 在各种优化算法中，共轭梯度法是非常重要的一种。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

具体的实现步骤请参加wiki百科共轭梯度法。下图为共轭梯度法和梯度下降法搜索最优解的路径对比示意图：

img