Pytorch（7）模型构建-nn

发表于 2022-05-02 更新于 2022-06-07 分类于【draft】工程，开源工具， Pytorch框架阅读次数：本文字数： 5.8k 阅读时长 ≈ 10 分钟

[PyTorch 学习笔记] 卷积层与nn.Conv

一、1D/2D/3D 卷积

卷积有一维卷积、二维卷积、三维卷积。一般情况下，卷积核在几个维度上滑动，就是几维卷积。比如在图片上的卷积就是二维卷积。

一维卷积：

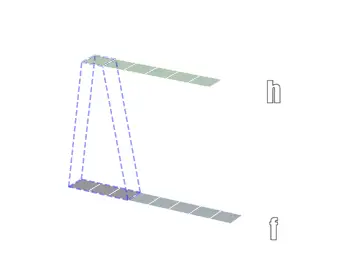
二维卷积：

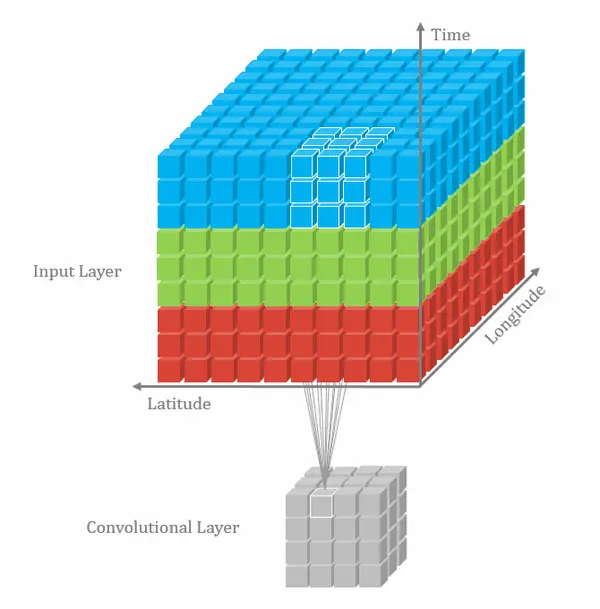
三维卷积：

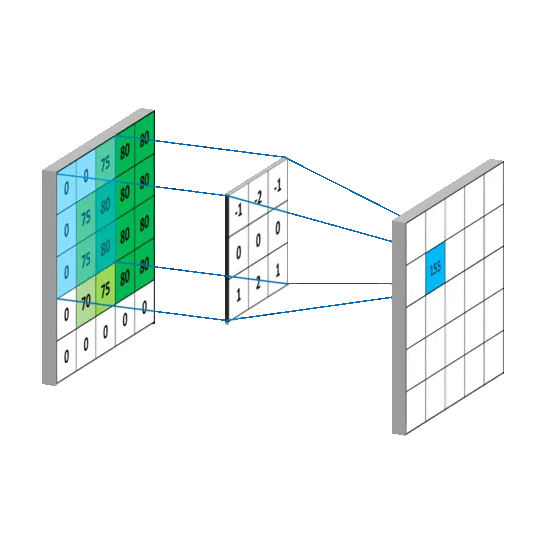
二、nn.Conv2d() 二维卷积

1
2
3

nn.Conv2d(self, in_channels, out_channels, kernel_size, stride=1,
                 padding=0, dilation=1, groups=1,
                 bias=True, padding_mode='zeros')

这个函数的功能是对多个二维信号进行二维卷积，主要参数如下：

in_channels：输入通道数
out_channels：输出通道数，等价于卷积核个数
kernel_size：卷积核尺寸
stride：步长
padding：填充宽度，主要是为了调整输出的特征图大小，一般把 padding 设置合适的值后，保持输入和输出的图像尺寸不变。
dilation：空洞卷积大小，默认为 1，这时是标准卷积，常用于图像分割任务中，主要是为了提升感受野
groups：分组卷积设置，主要是为了模型的轻量化，如在 ShuffleNet、MobileNet、SqueezeNet 中用到
bias：偏置

2.1 卷积尺寸计算（简化版）

这里不考虑空洞卷积，假设输入图片大小为 $I \times I$ ，卷积核大小为 $k \times k$ ，stride 为 $s$ ，padding 的像素数为 $p$ ，图片经过卷积之后的尺寸 $O$ 如下：

下面例子的输入图片大小为 $5 \times 5$ ，卷积大小为 $3 \times 3$ ，stride 为 1，padding 为 0，所以输出图片大小为 $\displaystyle\frac{5 -3 + 2 \times 0}{1} +1 = 3$ 。

2.2 卷积网络示例

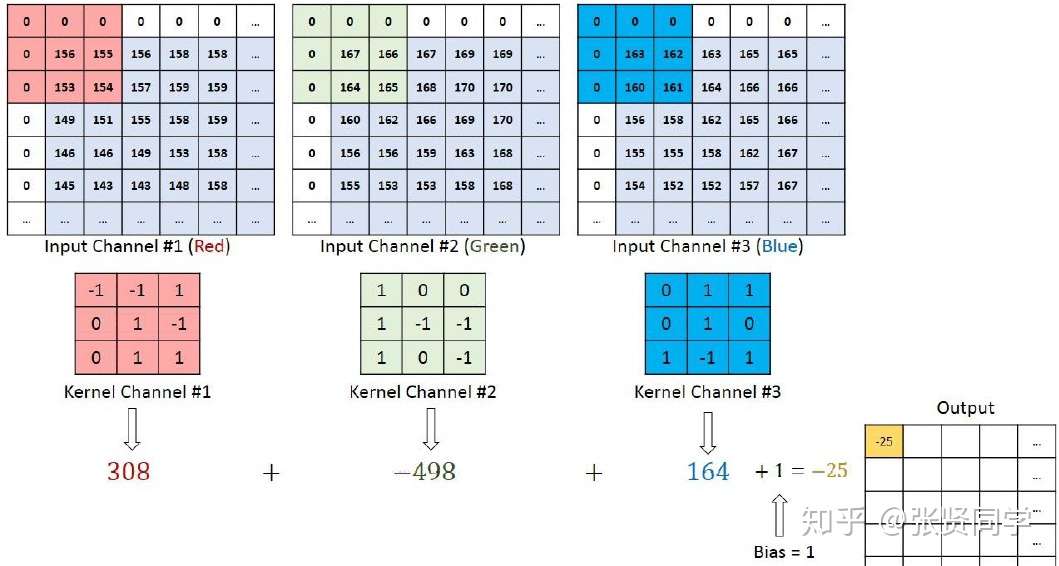
这里使用 input * channel 为 3，output_channel 为 1 ，卷积核大小为 $3 \times 3$ 的卷积核 nn.Conv2d(3, 1, 3)，使用 nn.init.xavier_normal_() 方法初始化网络的权值。代码如下：

conv_layer = nn.Conv2d(3, 1, 3)   
# 初始化卷积层权值
nn.init.xavier_normal_(conv_layer.weight.data)
img_conv = conv_layer(img_tensor)

我们通过conv_layer.weight.shape查看卷积核的 shape 是(1, 3, 3, 3)，对应是(output_channel, input_channel, kernel_size, kernel_size)。所以第一个维度对应的是卷积核的个数，每个卷积核都是(3,3,3)。虽然每个卷积核都是 3 维的，执行的却是 2 维卷积。下面这个图展示了这个过程。

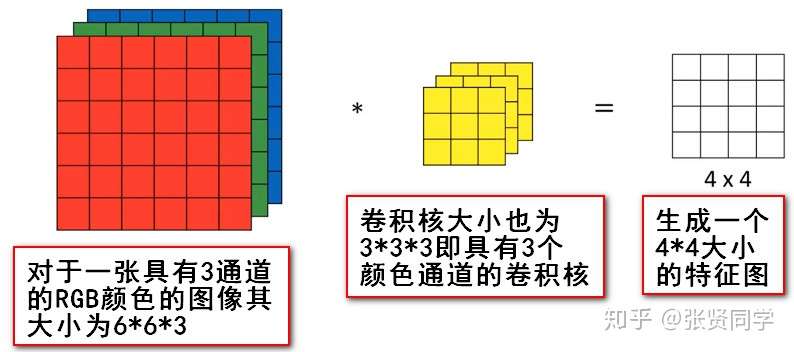
也就是每个卷积核在 input_channel 维度再划分，这里 input_channel 为 3，那么这时每个卷积核的 shape 是(3, 3)。3 个卷积核在输入图像的每个 channel 上卷积后得到 3 个数，把这 3 个数相加，再加上 bias，得到最后的一个输出。

三、nn.ConvTranspose() 转置卷积

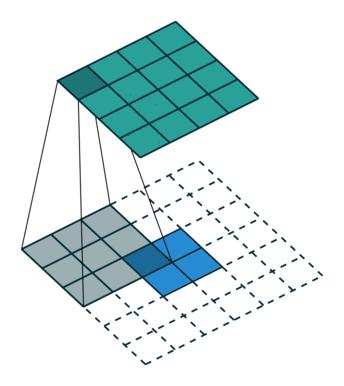
3.1 转置卷积原理

转置卷积又称为反卷积 (Deconvolution) 和部分跨越卷积 (Fractionally strided Convolution)，用于对图像进行上采样。

正常卷积如下：

原始的图片尺寸为 $4 \times 4$ ，卷积核大小为 $3 \times 3$ ， $padding =0$ ， $stride = 1$ 。由于卷积操作可以通过矩阵运算来解决，因此原始图片可以看作 $16 \times 1$ 的矩阵 $I_{16 \times 1}$ ，卷积核可以看作 $4 \times 16$ 的矩阵 $K_{4 \times 16}$ ，那么输出是 $K_{4 \times 16} \times I_{16 \times 1} = O_{4 \times 1}$ 。

转置卷积如下：

原始的图片尺寸为 $2 \times 2$ ，卷积核大小为 $3 \times 3$ ， $padding =0$ ， $stride = 1$ 。由于卷积操作可以通过矩阵运算来解决，因此原始图片可以看作 $4 \times 1$ 的矩阵 $I_{4 \times 1}$ ，卷积核可以看作 $4 \times 16$ 的矩阵 $K_{16 \times 4}$ ，那么输出是 $K_{16 \times 4} \times I_{4 \times 1} = O_{16 \times 1}$ 。

正常卷积核转置卷积矩阵的形状刚好是转置关系，因此称为转置卷积，但里面的权值不是一样的，卷积操作也是不可逆的。

PyTorch 中的转置卷积函数如下：

1
2
3

nn.ConvTranspose2d(self, in_channels, out_channels, kernel_size, stride=1,
                 padding=0, output_padding=0, groups=1, bias=True,
                 dilation=1, padding_mode='zeros')

和普通卷积的参数基本相同，不再赘述。

3.2 转置卷积尺寸计算

简化版转置卷积尺寸计算

这里不考虑空洞卷积，假设输入图片大小为 $I \times I$ ，卷积核大小为 $k \times k$ ，stride 为 $s$ ，padding 的像素数为 $p$ ，图片经过卷积之后的尺寸 $O$ 如下，刚好和普通卷积的计算是相反的：

转置卷积代码示例如下：

import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from common_tools import transform_invert, set_seed

set_seed(3)  # 设置随机种子

# load img 
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "imgs", "lena.png")
print(path_img)
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# 添加 batch 维度
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

# create convolution layer 
# flag = 1
flag = 0
if flag:
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    # 初始化卷积层权值
    nn.init.xavier_normal_(conv_layer.weight.data)
    # nn.init.xavier_uniform_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

#  transposed
flag = 1
# flag = 0
if flag:
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(input_channel, output_channel, size)
    # 初始化网络层的权值
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()

转置卷积前后图片显示如下，左边原图片的尺寸是 (512, 512)，右边转置卷积后的图片尺寸是 (1025, 1025)。

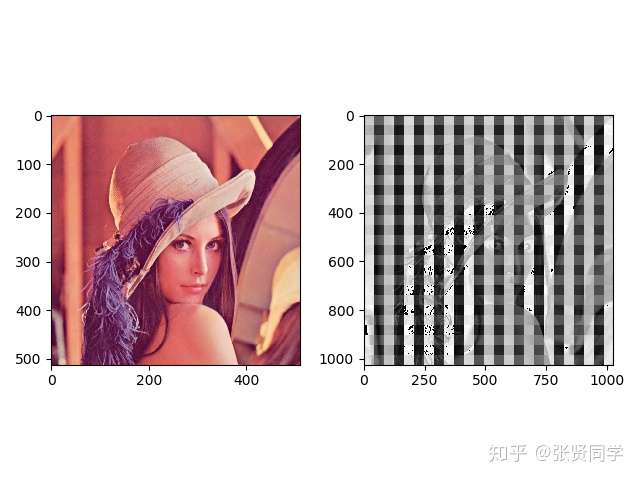
转置卷积后的图片一般都会有棋盘效应，像一格一格的棋盘，这是转置卷积的通病。

关于棋盘效应的解释以及解决方法，推荐阅读Deconvolution And Checkerboard Artifacts[1]。

3.3 DCGAN

生成器
- nz = 100 : 潜在向量 z 的大小
- ngf = 64 : 生成器中特征图的大小
- ndf = 64 : 判别器中的特征映射的大小

# 生成器代码
class Generator(nn.Module):
    def __init__(self, ngpu):
        super(Generator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # 输入是Z，进入卷积
            nn.ConvTranspose2d(nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # state size. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # state size. (ngf*4) x 8 x 8
            nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # state size. (ngf*2) x 16 x 16
            nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # state size. (ngf) x 32 x 32
            nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        return self.main(input)

判别器代码

class Discriminator(nn.Module):
    def __init__(self, ngpu):
        super(Discriminator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # input is (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        return self.main(input)

三、卷积参数更新

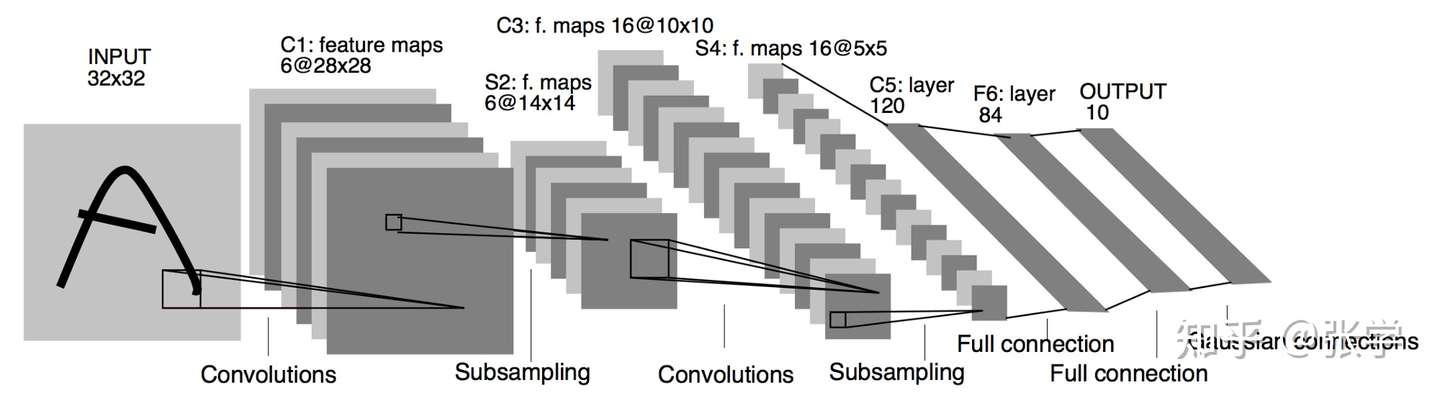
与全连接神经网络不同，卷积神经网络每一层中的节点并不是与前一层的所有神经元节点相连，而是只与前一层的部分节点相连。并且和每一个节点相连的那些通路的权重都是相同的。举例来说，对于二维卷积神经网络，其权重就是卷积核里面的那些值，这些值从上而下，从左到右要将图像中每个对应区域卷积一遍然后将积求和输入到下一层节点中激活，得到下一层的特征图。因此其权重和偏置更新公式与全连接神经网络不通。

降低的计算量
权重得到共享，降低了参数量

根据《Deep learning》这本书的描述，卷积神经网络有3个核心思想：

稀疏交互（sparse interactions），即每个节点通过固定个（一般等于卷积核元素的数目，远小于前一层节点数）连接与下一层的神经元节点相连; 尽管是稀疏连接，但是在更深层的神经单元中，其可以间接地连接到全部或大部分输入图像。如果采用了步幅卷积或者池化操作，那么这种间接连接全部图像的可能性将会增加。
参数共享（parameter sharing），以2D卷积为例，每一层都通过固定的卷积核产生下一层的特征图，而这个卷积核将从上到下、从左到右遍历图像每一个对应区域；
等变表示（equivariant representations），卷积和参数共享的形式使得神经网络具有平移等变形，即f(g(x))=g(f(x))。另外，pooling操作也可以使网络具有局部平移不变形。局部平移不变形是一个很有用的性质，尤其是当我们只关心某个特征是否出现而不关心它出现的具体位置时。池化可以看作增加了一个无线强的先验，这一层学的函数必须具有对少量平移的不变形。

3.1 正向传播

如何对卷积核数量和卷积步长进行选择?

卷积核的数量越多，意味着提取的特征种类越多，通常会取2^n个;
步长通常不会超过卷积核宽度或长度，步长大于1的时候有下采样的效果，比如步长为2时，可以让feature map的尺寸缩小一半。