理论基础(6)模型融合
模型融合
没有哪个机器学习模型可以常胜,如何找到当前问题的最优解是一个永恒的问题。
幸运的是,结合/融合/整合 (integration/ combination/ fusion)多个机器学习模型往往可以提高整体的预测能力。这是一种非常有效的提升手段,在多分类器系统(multi-classifier system)和集成学习(ensemble learning)中,融合都是最重要的一个步骤。
一般来说,模型融合或多或少都能提高的最终的预测能力,且一般不会比最优子模型差。举个实用的例子,Kaggle比赛中常用的stacking方法就是模型融合,通过结合多个各有所长的子学习器,我们实现了更好的预测结果。基本的理论假设是:不同的子模型在不同的数据上有不同的表达能力,我们可以结合他们擅长的部分,得到一个在各个方面都很“准确”的模型。当然,最基本的假设是子模型的误差是互相独立的,这个一般是不现实的。但即使子模型间的误差有相关性,适当的结合方法依然可以各取其长,从而达到提升效果。
我们今天介绍几种简单、有效的模型结合方法。
一、案例分析
让我们给出一个简单的分析。假设我们有天气数据X和对应的标签 \(\mathrm{y}\), 现在希望实现一个可以预测明天天气的模型 \(\psi\) 。但我们并不知道用什么算法效果最好, 于是尝试了十种算法, 包括
- 算法1: 逻辑回归- \(C_1\)
- 算法2: 支持向量机 (SVM) - \(C_2\)
- ...
- 算法10: 随机森林 - \(C_{10}\)
结果发现他们表现都一般,在验证集上的误分率比较高。我们现在期待找到一种方法,可以有效提高最终预测结果。
二、 平均法/投票法
一种比较直白的方法就是对让 10 个算法模型同时对需要预测的数据进行预测, 并对结果取平均数/众数。假设 10 个 分类器对于测试数据 \(X_t\) 的预测结果是 \(\left[C_1\left(X_t\right), C_2\left(X_t\right), \ldots, C_{10}\left(X_t\right)\right]=[0,1,1,1,1,1,0,1,1,0]\) ,那很显然少数服 从多数, 我们应该选择1作为 \(X_t\) 的预测结果。如果取平均值的话也可以那么会得到 0.7 , 高于阈值 0.5 , 因此是等 价的。
但这个时候需要有几个注意的地方:
首先,不同分类器的输出结果取值范围不同,不一定是[0,1],而可以是无限定范围的值。举例,逻辑回归的输出范围是0-1(概率),而k-近邻的输出结果可以是大于0的任意实数,其他算法的输出范围可能是负数。因此整合多个分类器时,需要注意不同分类器的输出范围,并统一这个取值范围。
- 比如可以先转化为如二分类结果,把输出的范围统一后再进行整合。但这种方法的问题在于我们丢失了很多信息,0.5和0.99都会被转化为1,但明显其可靠程度差别很大。
- 也可以转化为排序(ranking),再对不同的ranking进行求平均。
- 更加稳妥的方法是对每个分类器的输出结果做标准化,也就是调整到正态分布上去。之后就可以对多个调整后的结果进行整合。同理,用归一化也可以有类似的效果。
其次,就是整合稳定性的问题。采用平均法的另一个风险在于可能被极值所影响。正态分布的取值是 \([-\infty,+\infty]\) ,在少数情况下平均值会受到少数极值的影响。一个常见的解决方法是,用中位数(median)来代替平均数进行整合。
同时,模型整合面临的另一个问题是子模型良莠不齐。如果10个模型中有1个表现非常差,那么会拖累最终的效果,适得其反。因此,简单、粗暴的把所有子模型通过平均法整合起来效果往往一般。
三、寻找优秀的子模型准而不同
不难看出,一个较差的子模型会拖累整体的集成表现,那么这就涉及到另一个问题?什么样的子模型是优秀的。
一般来说,我们希望子模型:准而不同 -> accurate but diversified。好的子模型应该首先是准确的,这样才会有所帮助。其次不同子模型间应该有差别,比如独立的误差,这样作为一个整体才能起到互补作用。
因此,如果想实现良好的结合效果,就必须对子模型进行筛选,去粗取精。在这里我们需要做出一点解释,我们今天说的融合方法和bagging还有boosting中的思路不大相同。bagging和boosting中的子模型都是很简单的且基数庞大,而我们今天的模型融合是结合少量但较为复杂的模型。
四、筛选方法:赋予不同子模型不同的权重
因此我们不能再简单的取平均了, 而应该给优秀的子模型更大的权重。在这种前提下, 一个比较直白的方法就是根 据子模型的准确率给出一个参考权重 \(w\) ,子模型越准确那么它的权重就更大, 对于最终预测的影响就更强: \(w_i=\frac{A c c\left(C_i\right)}{\sum_1^{10} A c c\left(C_j\right)}\) 。简单取平均是这个方法的一个特例, 即假设子模型准确率一致。
五、更进一步:学习分类器权重
在4中提到的方法在一定程度上可以缓解问题,但效果有限。那么另一个思路是,我们是否可以学习每个分类器的权重呢?
答案是肯定,这也就是Stacking的核心思路。通过增加一层来学习子模型的权重。
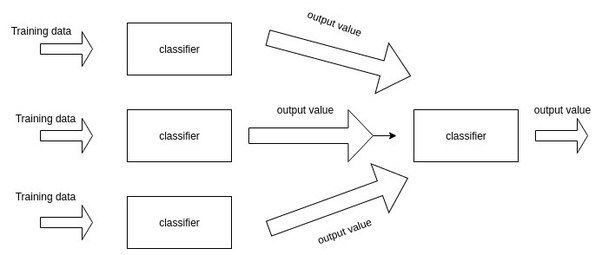
图片来源:https://www.quora.com/What-is-stacking-in-machine-learning
更多有关于stacking的讨论可以参考我最近的文章:集成学习总结-Stacking和神经网络。简单来说,就是加一层逻辑回归或者SVM,把子模型的输出结果当做训练数据,来自动赋予不同子模型不同的权重。
一般来看,这种方法只要使用得当,效果应该比简单取平均值、或者根据准确度计算权重的效果会更好。