风控模型
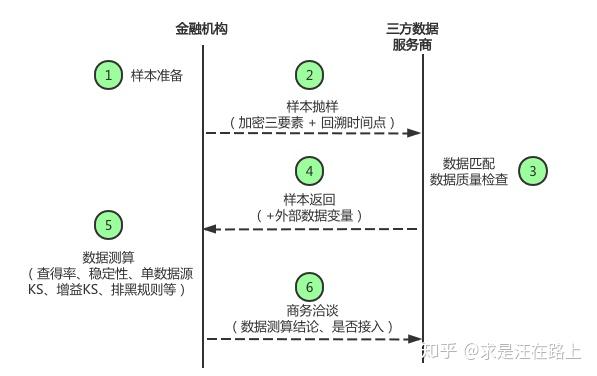
求是汪在路上:多头借贷风险分析与建模
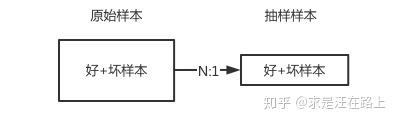
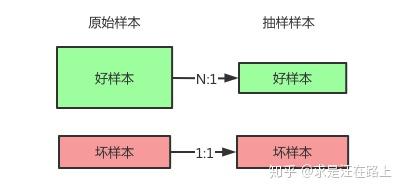
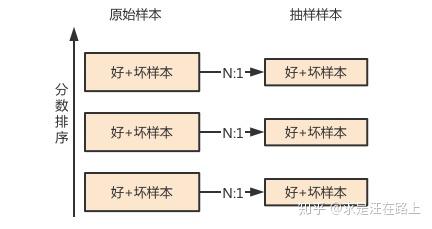
求是汪在路上:抽样对Lift和KS指标的影响
求是汪在路上:客户级通用信用评分模型架构设计
求是汪在路上:大数据信贷风控模型架构
求是汪在路上:
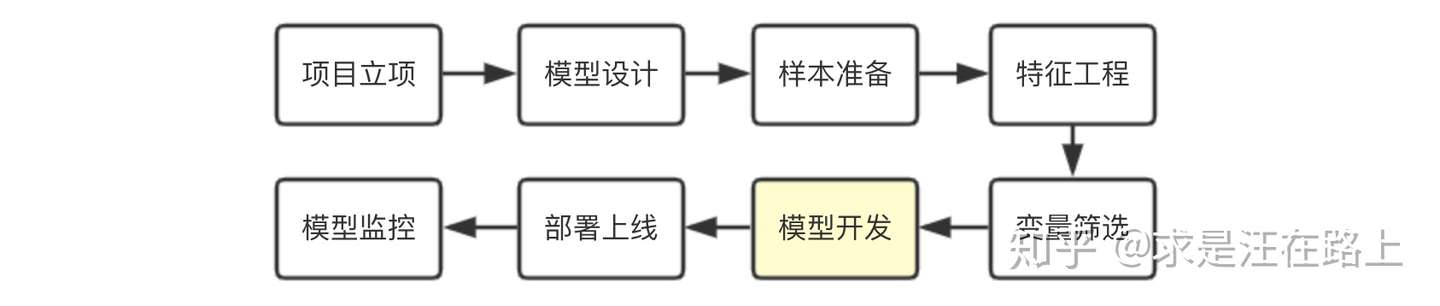
风控模型开发流程标准化
求是汪在路上:风控模型上线部署流程
求是汪在路上:如何量化样本偏差对信贷风控模型的影响
求是汪在路上:
样本权重对逻辑回归评分卡的影响探讨
求是汪在路上:利用样本分群提升风控模型性能
一、风控模型开发流程标准化 风控业务背景 在大型风控建模项目中,模型开发阶段实际上只占其中很小的一部分,我们常把大量精力投入在数据准备、特征工程、模型设计等阶段。同时,开发阶段所用方法重复性相对较高。如果将其模块化封装,可大大提高建模效率。Don‘t
repeat yourself!
img
本文主要内容在于:
理论角度,系统阐述了风控模型开发流程,以及相应的理论依据。
实践角度,整理了目前一些开源工具包,可供大家自行选择使用。
1.1
风控模型开发流程标准化的意义 在《大数据信贷风控模型架构 》一文中,我们系统探讨了大数据风控模型架构的优缺点。从该架构出发,基于历次大型模型开发项目实践,我们往往会发现存在以下问题:
各建模同学的工程能力存在差异,无法保证所有人都有代码优化及debug的能力。
整个流程不规范统一,某些同学不清楚基础指标函数的底层逻辑,出现问题难以定位。
浪费大量时间用于协调沟通,尤其是过程文档记录参差不齐,无法复现。
建模脚本可能存在多个版本,模型版本管理困难 。
风控模型开发流程标准化的意义在于:
提高建模效率:可批量快速生产模型,保证项目按期完成,同时让建模同学更有精力关注模型优化分析等复杂工作。
理解计算逻辑:帮助团队更为深刻理解各类评估指标背后的业务含义,便于调试优化。
统一建模流程 :约定命名方式。保证在分工协作的情况下,模型开发文档更容易整合汇总,便于Review。流程规范约束:减少建模同学(尤其是新手)出错的概率,降低返工可能,并记录必要的中间过程,便于问题回溯。
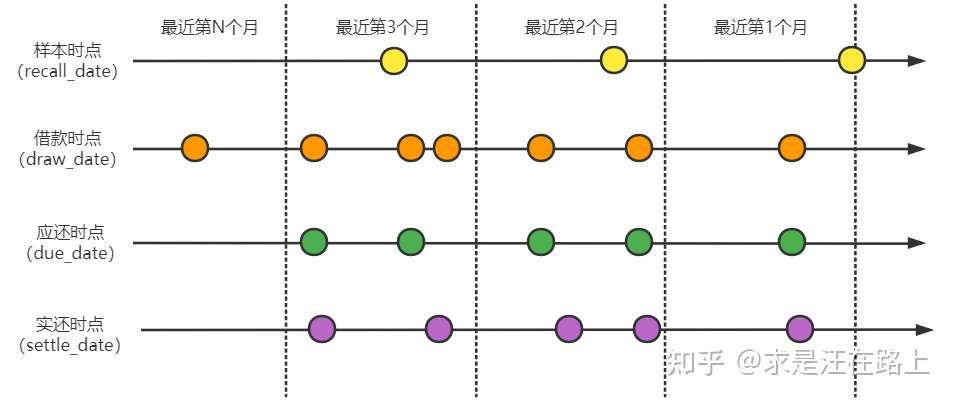
由于经常需要跨时间窗来分析变量,我们约定以下名词:
样本集 :训练集(In the Sample,INS)、验证集(Out
of Sample,OOS)、测试集(Out of Time,OOT)自然月 :由于风控领域中样本相对较少,一般按月粒度来观察。对于某段时间内的样本,我们也称为cohort或vintage。通俗而言,就是一个批次(batch)。
1.2 功能模块 -
探索性数据分析 探索性数据分析(Exploratory Data
Analysis,EDA)用于初步检验数据质量,因此需要计算各类数据特征指标。
探索数据分布(Exploratory Data Distribution,EDD)
缺失率(Missing Rate)
重复值(Duplicate Value)
单一值(Unique Value)
其他数据质量检查(Quality Check)
1.2.1
探索数据分布(Exploratory Data Distribution,EDD) 功能 :按自然月/样本集维度,统计变量的数据分布。
指标 :
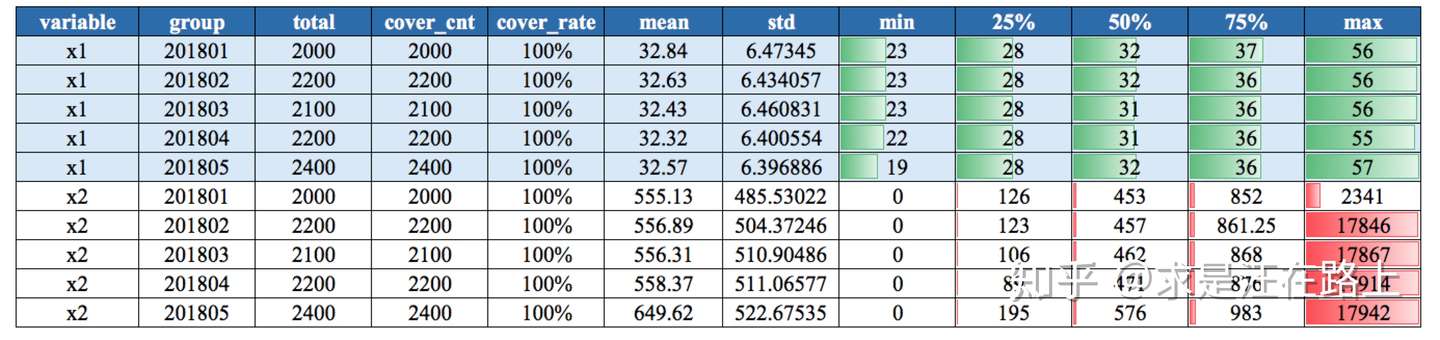
连续型变量,包括:数量(count)、均值(mean)、标准差(std)、最小值(min)、分位数P25、P50、P75、最大值(max)。其中,最大值和最小值可用来观察异常值(outlier)。
离散型变量,包括:取值及出现次数(cnt)、占比(ratio)。
示例 :连续变量数据分布(月维度)、离散变量数据分布
img
img
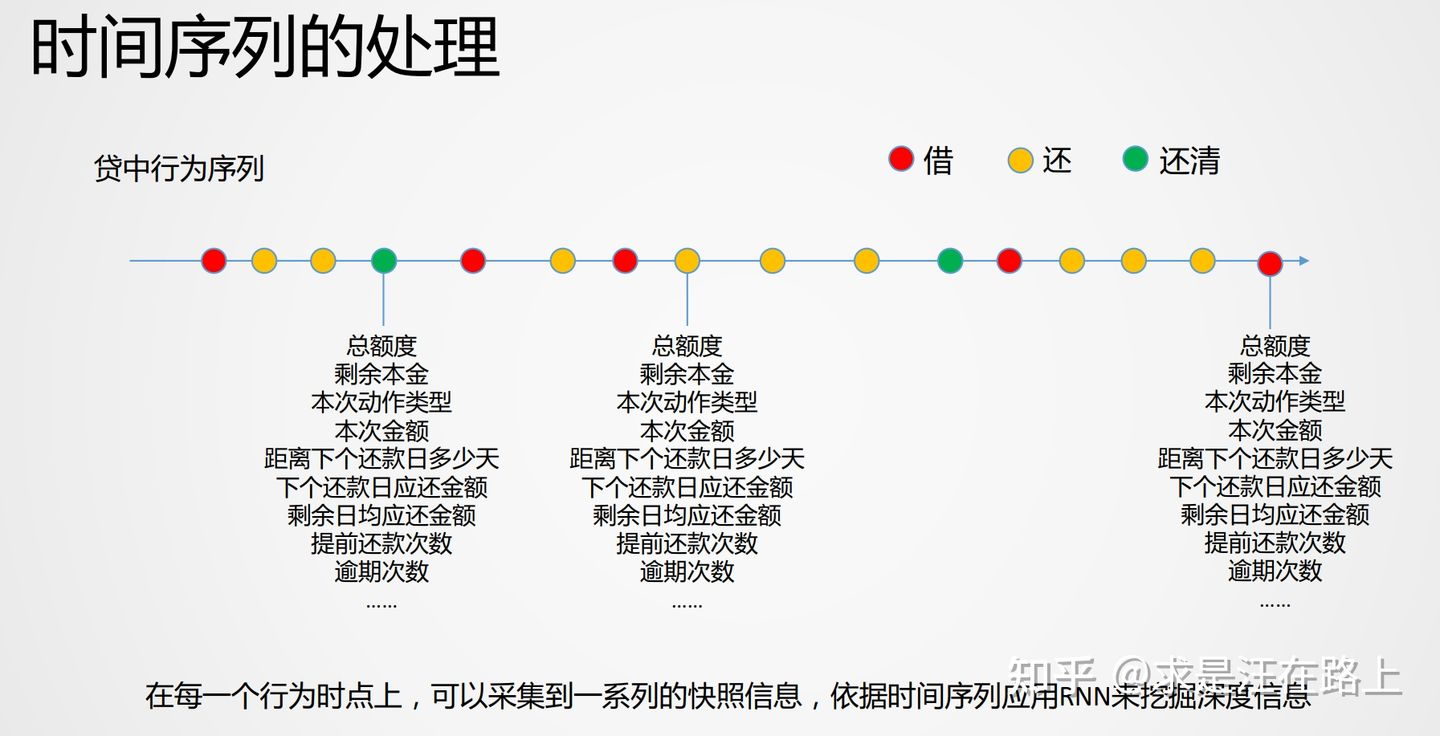
业务含义 :基于“历史与未来样本分布相同 ”的建模假设,我们才能基于历史数据拟合X和Y之间的关系来预测未来。因此,在变量分布上,首先需要保证这一点。
从图1中,我们可以观察分位数的变化差异。例如,变量
1.2.2 缺失率(Missing
Rate) 功能:按自然月/样本集维度,统计变量的缺失率。
指标:缺失率 = 未覆盖样本数 / 总样本数 × 100%
img
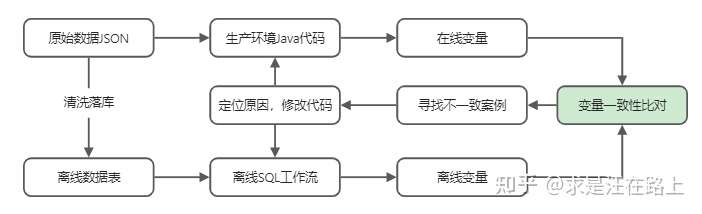
业务:
用于分析数据源的缺失率,以及未来的采集率趋势。如果缺失率持续升高,我们就认为这块数据不可用。
造成缺失的原因多种多样,可分为随机缺失和非随机缺失。例如,如果是用户自填信息,用户主观不愿意填写而导致数据缺失,属于非随机缺失。
1.2.3 重复值(Duplicate
Value) 功能:检验建模样本中是否有重复数据。
指标:按样本ID分组后,统计行数
img
业务:观察相同订单的特征变量取值是否一致。取值相同,只需简单去重;否则,说明生成逻辑有误,需检查SQL逻辑。
1.2.4 单一值(Unique
Value) 功能:统计变量中某一固定值的占比。
指标:变量每个取值的出现次数。
示例:变量中0的取值占到70%.
业务:如果变量取值中某一固定值占比很高,那么该变量区别度往往很低。通常,单一值比例超过90%以上,建议删除该变量。
1.2.5
其他数据质量检查(QC) 变量取值本身具有某些业务含义,我们需要结合业务来检验,并记录归档。例如:
特殊值归档说明:例如-9999999是代表缺失,还是其他含义,需给出描述说明。
0的业务逻辑确认:真实值为0?数据缺失?默认填充值?
1.3 功能模块 -
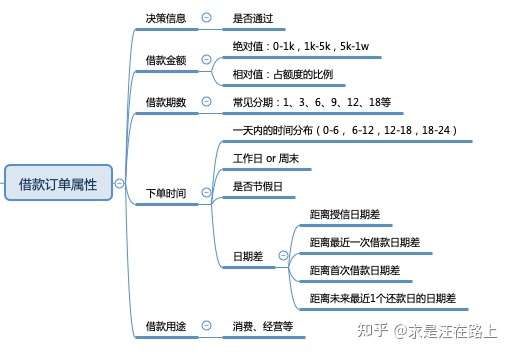
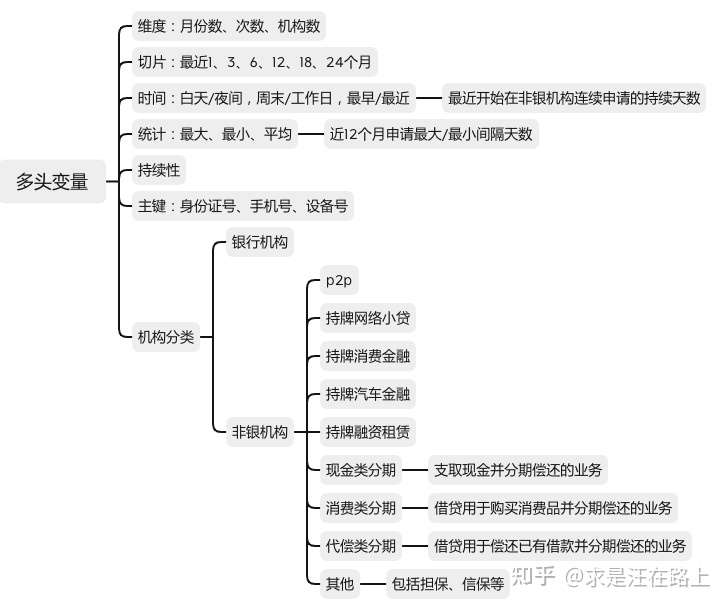
特征选择 根据RFM特征体系,我们可以构造成千上万个特征变量(参考《风控特征—时间滑窗统计特征体系 》)。但是,这些变量并不都满足我们的要求,
我们需要剔除不符合要求的变量,从输入上保证风控系统的鲁棒性。
变量筛选(selection)是一个比较复杂的精细活,需要考虑很多因素,比如:预测能力、相关性、稳定性、合规性、业务可解释性 等等。考虑不同维度,我们会依据一系列指标进行变量筛选。
从广义上,可分为业务指标和技术指标两大类。
1.3.1 业务指标 包括:
合规性(compliant) :用以加工变量的数据源是否符合国家法律法规?是否涉及用户隐私数据?例如,如果某块爬虫数据被监管,那么相关变量的区分度再好,我们也只能弃用。而在国外,种族、性别、宗教等变量被禁止用于信贷风控中,这会存在歧视性。可得性(available) :数据未来是否能继续采集?这就涉及产品流程设计、用户授权协议、合规需求、模型应用环节等诸多方面。例如,如果产品业务流程改动而导致某个埋点下线,那么相关埋点行为变量只能弃用。又比如,如果需要做额度授信模型,那么只能利用在额度阶段能采集到的实时数据,这就需要提前确认数据采集逻辑。稳定性(stable) :一方面,数据源采集稳定是变量稳定性的基本前提。例如,外部数据常会因为政策性、技术性等原因导致接入不稳定,这就需要做好数据缓存,或者模型降级机制。另一方面,变量取值分布变化是导致不稳定的直接原因。我们将会采取一些技术指标展开分析,下文将会介绍。可解释性(interpretable) :需要符合业务可解释性。如果变量的业务逻辑不清晰,那么我们宁可弃之。同时,这也是保证模型可解释性(参数
+ 变量)的前提。逻辑性(logical) :也就是因果逻辑,特征变量是因,风控决策是果。如果某个变量是风控系统决策给出的,那么我们就不能入模。例如,用户历史申贷订单的利率是基于上一次风控系统决策的结果,如果将“用户历史申贷订单的利率”作为变量,那么在实际使用时就会有问题。可实时上线 :模型最终目的是为了上线使用。如果实时变量不支持加工,那么对应的离线变量就只能弃之。例如,某个离线变量在统计时限定观察期为180天,但线上只支持观察期为90天,那么就不可用。对于不熟悉线上变量加工逻辑的新手,往往容易踩坑而导致返工。
1.3.2 技术指标 包括:
基于缺失率(Missing Rate) 基于变异系数(Coefficient of
Variation,CV) 基于稳定性(Population Stability Index,PSI)
基于信息量(Information Value,IV) 基于RF/XGBoost特征重要性(Feature
Importance) 变量聚类(Variable Cluster,VarClus)
基于线性相关性(Linear Correlation) 基于多重共线性(Multicollinearity)
基于逐步回归(stepwise) 基于P-Vaule显著性检验
业务: 变量缺失率越高,可利用价值越低。缺失率变化不稳定的变量,尤其是缺失率趋势在升高,代表未来数据源采集率下降,不建议采用。数据源是特征变量的基础,数据源不稳定,直接导致模型稳定性变差。
功能:
step 1.
按自然月/样本集维度,统计变量缺失率,并计算缺失率的均值、标准差。 step
2. 根据实际场景,设置阈值(如50%、70%、90%)进行筛选。
img
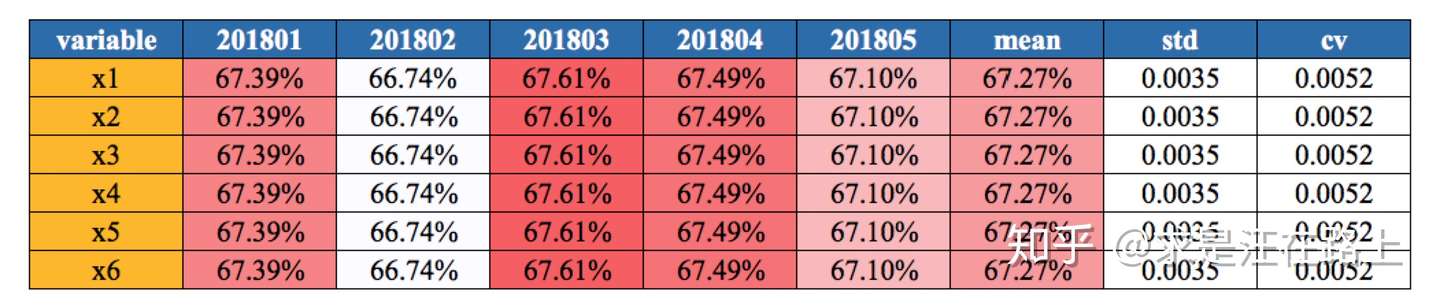
基于变异系数(Coefficient of Variation,CV)
业务 :变异系数越小,代表波动越小,稳定性越好。缺点在于CV没有统一的经验标准。
功能 :
step 1.
基于数据分布EDD,选择某个指标(如均值mean)计算变异系数CV,用来衡量变量分布的稳定性。
step 2. 设置阈值进行筛选。
指标 :变异系数 C·V =( 标准偏差 SD / 平均值Mean )×
100%
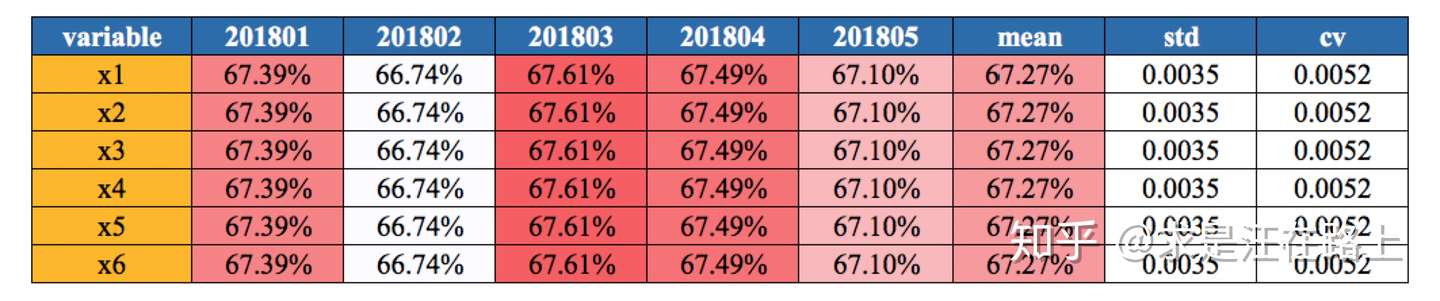
基于稳定性(Population Stability Index,PSI)
业务 :需分申请层、放款层,分别评估变量稳定性。通常会选择0.1作为阈值,只要任意一个不满足稳定性要求就弃用。PSI无法反映很多细节原因,比如分布是右偏还是左偏。此时需要从EDD上进行分析。
img
功能 :
step 1. 以训练集(INS)分布为期望分布,计算变量的群体稳定性指标PSI。
step 2. 根据PSI的经验阈值进行筛选。
指标 :
上式含义为:PSI = SUM( (实际占比 - 预期占比)* ln(实际占比 /
预期占比)
);预期占比是指训练集上每个分箱里的样本占比,实际占比是待比较样本集的每个分箱里的样本占比。可参考《群体稳定性指标(PSI)深入理解应用 》。
img
==基于信息量(Information Value,IV) ==
业务 :用以评估变量的预测能力 。通常情况下,IV越高,预测能力越强。但IV过高时,我们就要怀疑是否发生信息泄漏(leakage)问题,也就是在自变量X中引入了Y的信息。
img
功能 :
step 1. 按自然月/样本集维度,统计变量的IV。 step 2.
根据IV的经验阈值来筛选。
指标 :IV。可参考《 WOE与IV指标的深入理解应用 》
[公式]
img
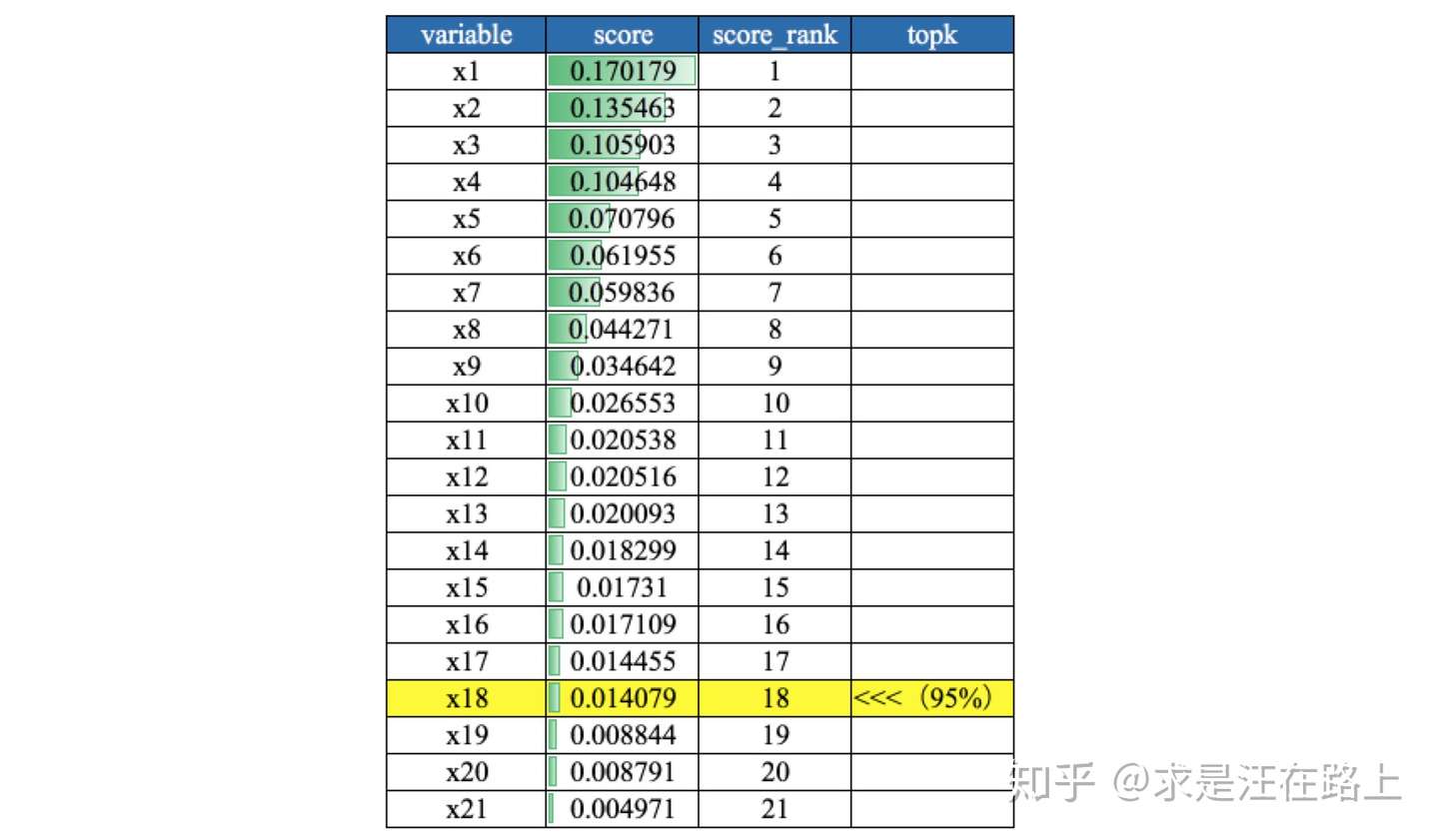
业务 :在特征变量特别多的时候,可用于快速筛选特征。从机器学习可解释性角度而言,特征重要性只具有全局可解释性,无法对单个case给出解释。
功能 :
step 1. 根据树模型训练后给出的特征重要性,一般选择累积重要性Top
95%的变量。 step 2.
为降低一次训练所导致的随机性影响,可综合多次结果来筛选。
指标:特征重要性。XGBoost实现中Booster类get_score方法输出特征重要性,其中
importance_type参数支持三种特征重要性的计算方法:
weight(默认值):使用特征在所有树中作为划分属性的次数。 gain:使用特征在作为划分属性时,OBj的平均降低量。 cover:使用特征在作为划分属性时对样本的覆盖度。
RF中计算特征重要度的主要思想:影响力分析 。如果某个输入变量产生扰动,导致模型系统输出性能(利用袋外数据OOB的准确率来评估)产生明显影响,那么说明输入变量对系统具有较大的影响力,特征重要度比较高。
执行步骤为:
step 1. 基准性能:对每一颗决策树,选择相应的袋外数据计算误差,记为
img
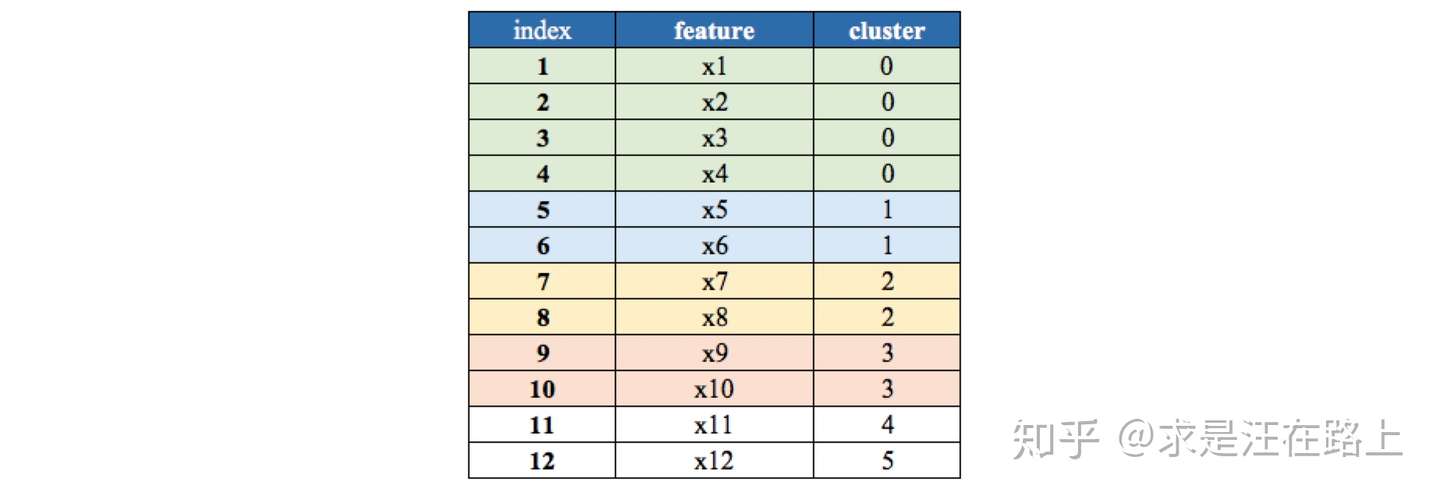
变量聚类(Variable Cluster,VarClus)
业务 :在SAS中对应Proc VarClus方法。
功能 :
step 1. 列聚类,将所有变量进行层次聚类。 step 2.
根据聚类结果,剔除IV相对较低的变量。
指标 :
1 2 3 4 5 6 7 from sklearn.cluster import FeatureAgglomerationfrom sklearn import preprocessing X_Scale = preprocessing.StandardScaler().fit_transform(input_df[var_list]) ward = FeatureAgglomeration(n_clusters=n_clusters, linkage='ward' ) ward.fit(X_Scale) clusters = list (ward.labels_)
img
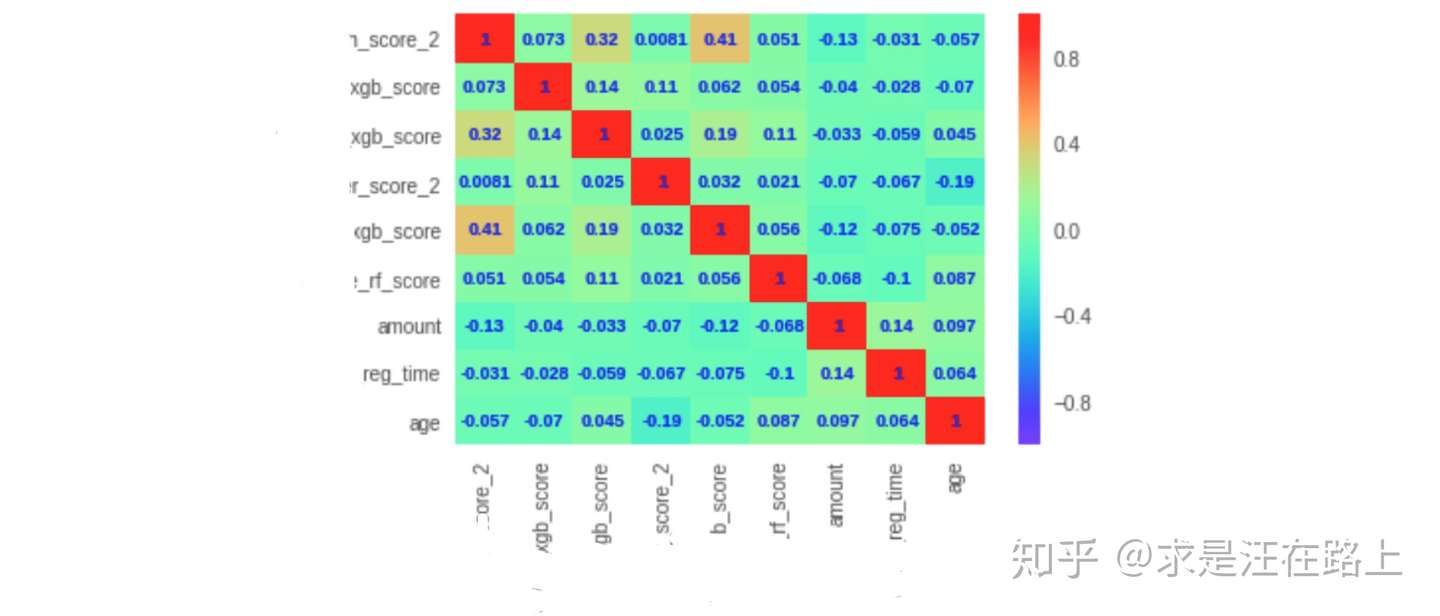
基于线性相关性(Linear Correlation)
业务 :逻辑回归作为一种线性模型,其基础假设是:自变量
功能 :
step 1. 计算变量的线性相关性。 step 2.
相关性较高的多个变量里,保留IV较高的变量。
指标 :皮尔逊相关系数(Pearson Correlation
Coefficient) ,系数的取值为
[公式]
img
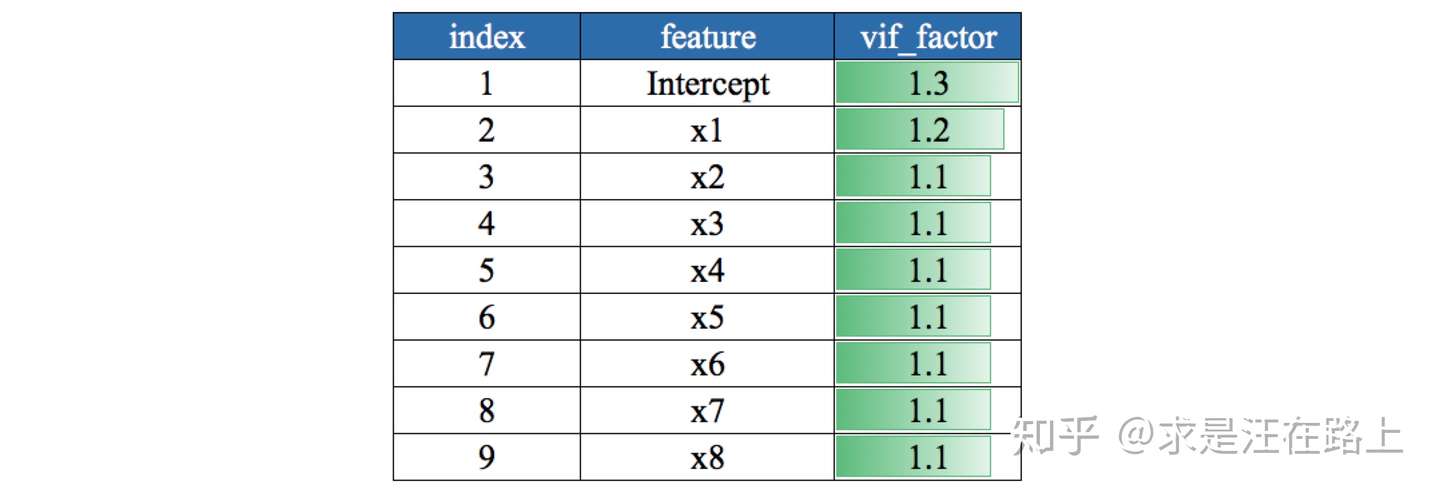
基于多重共线性(Multicollinearity)
对于自变量
[公式]
换言之,对于
当出现多重共线性时,变量之间的联动关系会导致估计标准差偏大,置信区间变宽。这就会产生一个常见的现象,LR中变量系数出现正负号不一致。
业务:VIF取值的业务含义为:
若VIF < 3,说明基本不存在多重共线性问题 若VIF >
10,说明问题比较严重。
功能:
step 1. 计算变量的方差膨胀因子(Variance Inflation
Factor,VIF),适用于线性模型。 step 2.
根据阈值剔除VIF较高的变量。
指标:通常用VIF衡量一个变量和其他变量的多重共线性。
1 from statsmodels.stats.outliers_influence import variance_inflation_factor
示例:
img
基于逐步回归(stepwise)
前向选择(forward
selection):逐步加入变量,计算指标进行评估,若不合格则不加入,直到评估完所有变量。
后向选择(backward
selection):初始时加入所有变量,根据指标逐渐剔除不合格的变量。
逐步选择(stepwise):将向前选择和向后选择的结合,逐步放入最优的变量、移除最差的变量。
基于P-Vaule显著性检验
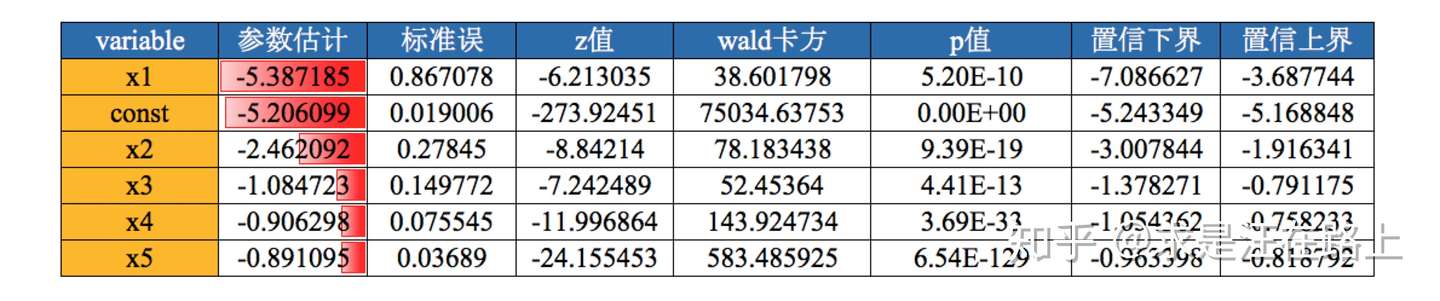
业务:根据逻辑回归参数估计表,剔除P值大于0.05的变量。
功能:
step 1. 用于检验自变量X与因变量Y之间的相关性。 step 2.
剔除P值大于0.05的变量。
指标:P-Vaule。在变量相关分析中,对相关系数进行假设检验时:
原假设H0:自变量与因变量之间线性无关。
备择假设H1:自变量与因变量之间线性相关。
或许不太恰当,但通常当P值大于0.05时,接受原假设,否则拒绝原假设。因此,我们需要剔除P值大于0.05的变量。
img
1.4 功能模块 -
模型训练 该模块主要包括变量变换(如分箱) 、样本准备(包括样本赋权、拒绝推断等) 、模型参数估计 、模型分数校准 、模型文件保存 等功能。
1.4.1 WOE转换(Weight of
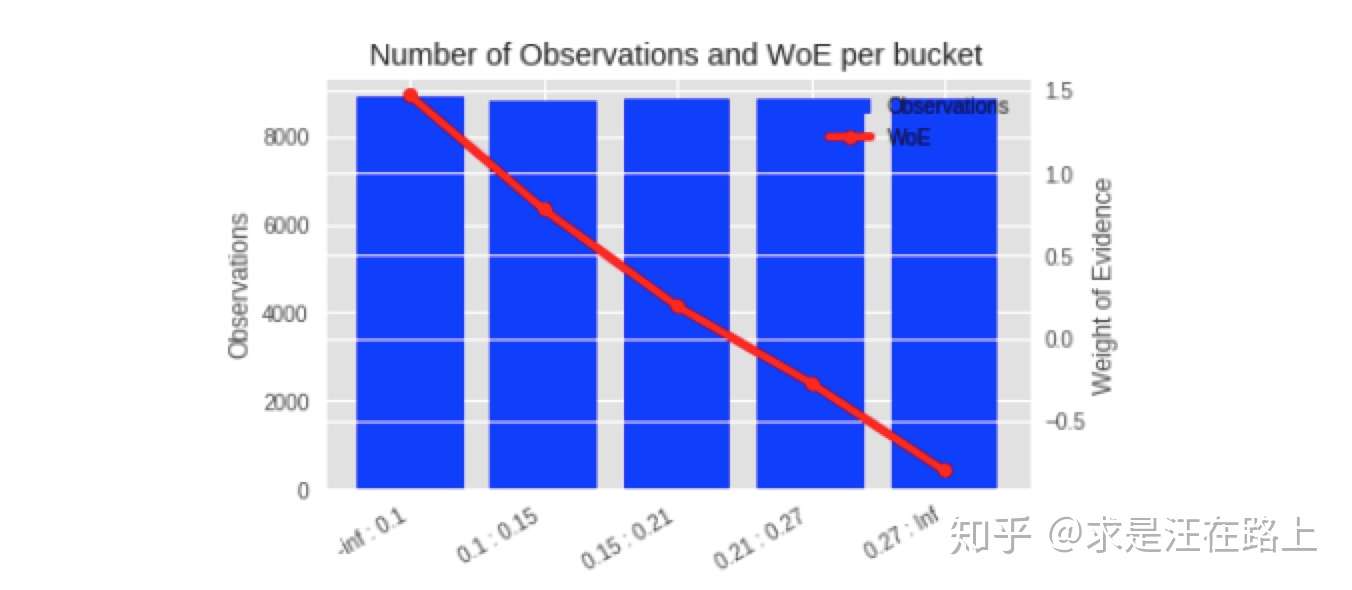
Evidence) 业务:训练集上的WOE曲线需满足单调性,并且经过跨时间窗验证WOE变换逻辑同样满足单调性。如果不满足,那就需要再次调整。
功能:在评分卡模型中用于变量WOE变换,支持等频、等距、自定义间距等分箱操作。
原理:可参考《 WOE与IV指标的深入理解应用 》
示例:
img
1.4.2 样本权重(Sample
Weight) 功能:给建模样本赋予权重列,以逼近总体样本。
原理:建模本质在于从历史样本中学习未来样本的数理统计规律。
不同的样本权重主要有几个目的:
为了让模型更稳健,一般都是拿近期样本refit模型,但上线后没几个月很快就衰减了,说明训练样本有偏程度比较高,不够代表总体。
早期的历史样本都是拿钱换来的,如何把这部分样本利用起来,不浪费。
==业务角度(主观性强,操作性高):==
按时间因素,近期样本提高权重,较远样本降低权重
按贷款类型,不同额度、利率、期限的样本赋予不同权重
按样本分群,不同群体赋予不同权重
技术角度(操作性复杂,可解释性弱):
借鉴Adaboost思想,对误判样本提高权重
过采样、欠采样、SMOTE等
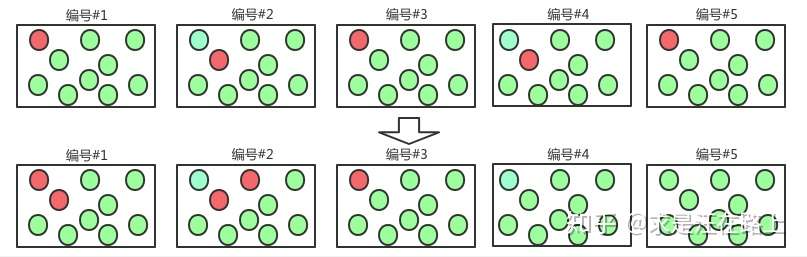
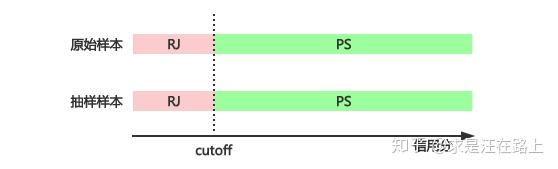
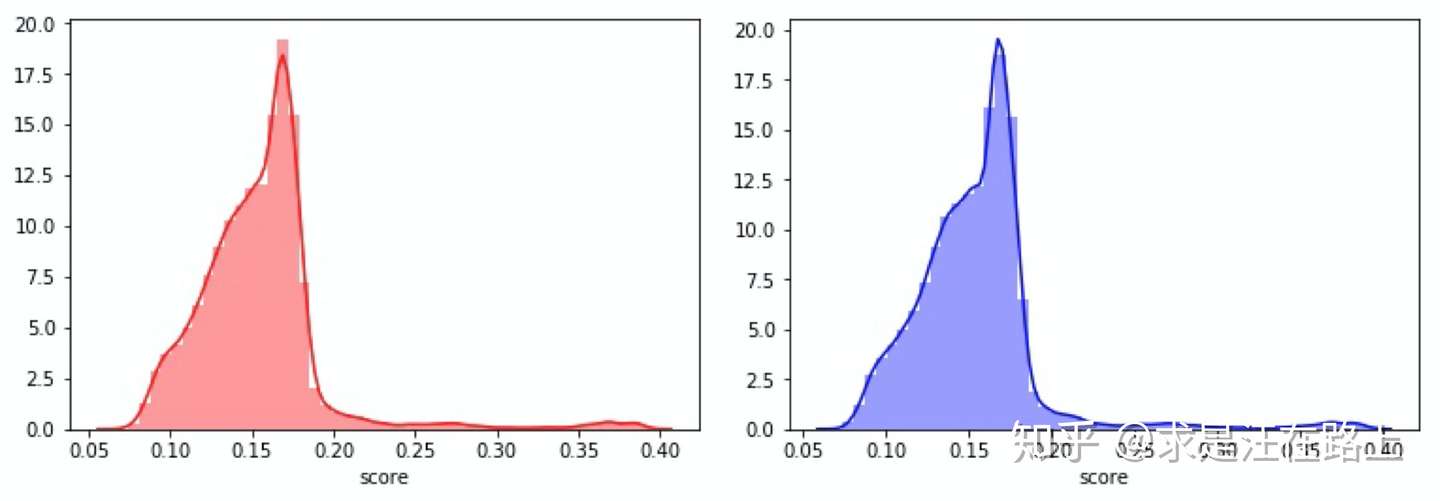
拒绝演绎(Reject
Inference) 功能:样本偏差将会导致模型估计过于乐观。通过推断拒绝样本的贷后表现,加入建模样本,可降低放贷建模样本与申请作用样本之间的偏差。
原理:参考《风控建模中的样本偏差与拒绝推断 》
参数估计(Parameter
Estimation) 功能:支持机器学习模型(如随机森林、GBDT、XGBoost、LightGBM等)调参、评分卡模型逐步回归(stepwise)。
原理:LR采用最大似然估计进行参数估计。而机器学习模型的超参数较多,通常需要借助网格搜索(grid
search)、贝叶斯调参等技术,降低对人工经验的依赖。
分数校准(Calibration) 功能:其一,一致性校准,将模型预测概率校准到真实概率。其二,尺度变换,将风险概率转换为平时所见的整数分数。
原理:参考《信用评分卡模型分数校准 》
模型保存(Save Model) 功能:将模型(参数+结构)保存为pkl和pmml文件,用以最终上线部署。注意需要给不同版本的模型赋予易于辨识、含义清晰的命名。一般建议至少包含以下内容:
命名 = 生成日期+责任人+业务线+应用环节+版本号
例如:20190101_小王_有钱花_额度授信_V1.pmml
原理:参考《风控模型上线部署流程 》
1.5 功能模块 -
模型评估 在实际业务实践中,我们对风控模型的衡量维度主要包括以下几个方面:
稳定性(Stability)
区分度(Discrimination)
排序性(Ranking)
拟合度(Goodness of Fit)
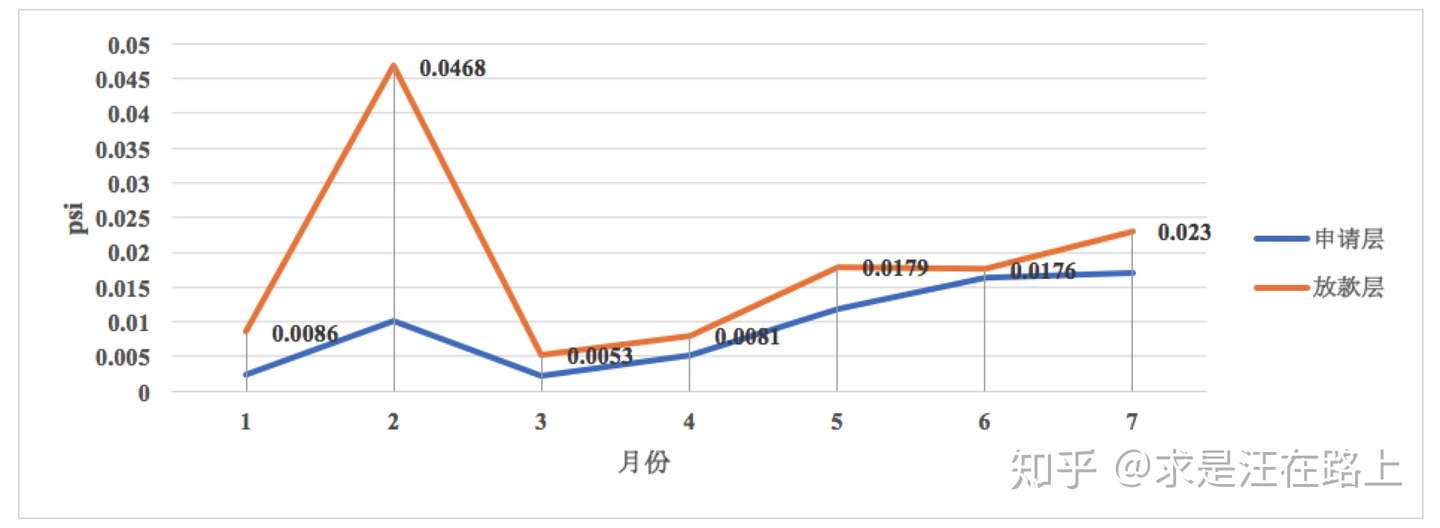
1.5.1 稳定性(Stability) 业务:在风控中,稳定性压倒一切。PSI取值所对应的业务含义如图8所示。我们需在申请层和放贷层上评估稳定性。原因在于:
虽然模型是基于放贷订单训练,但最终应用在申请层。
申请层和放贷层客群存在差异。
当PSI曲线的趋势一直在上升时,我们就要分析原因,消除不稳定因素。排查方向可参考《特征稳定性指标(CSI)深入理解应用 》中的Part
4。
指标:PSI。可参考《群体稳定性指标(PSI)深入理解应用 》
示例:
img
1.5.2
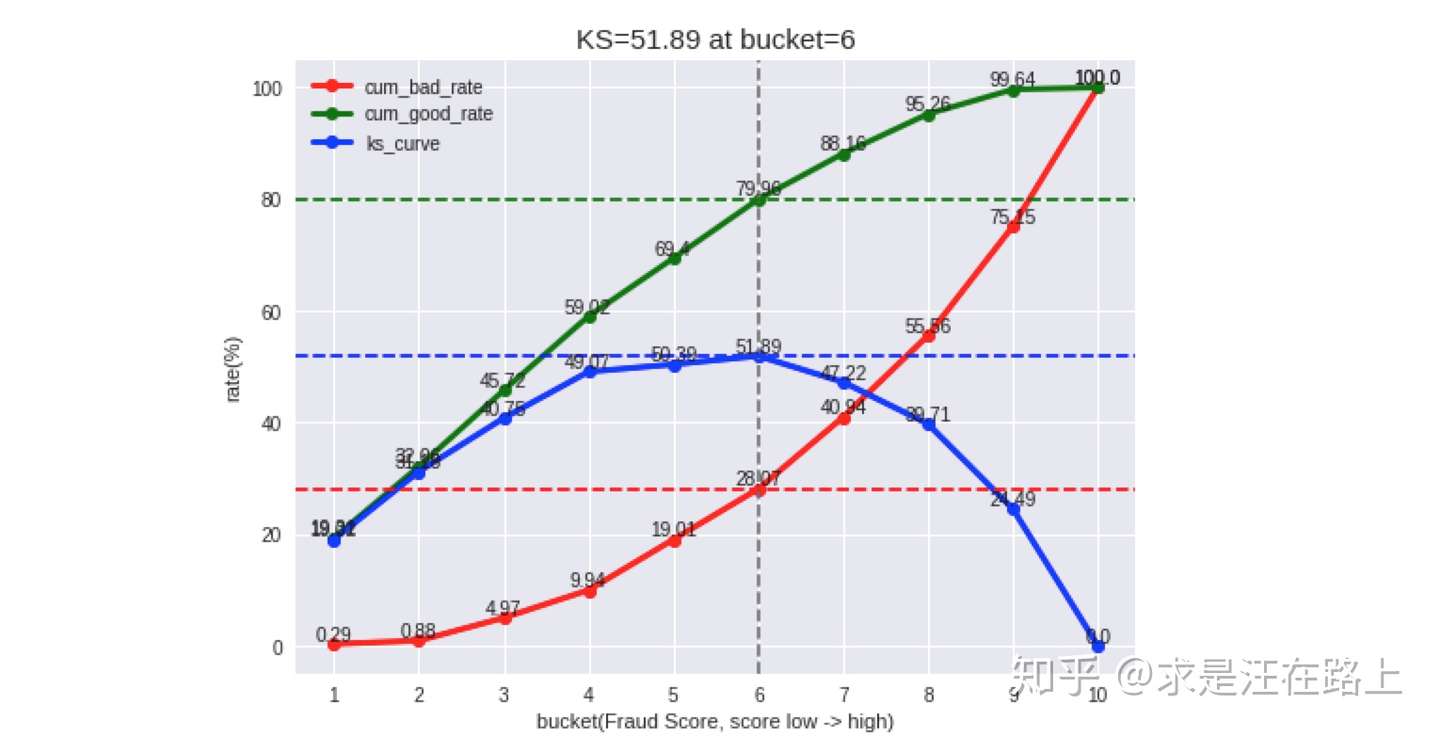
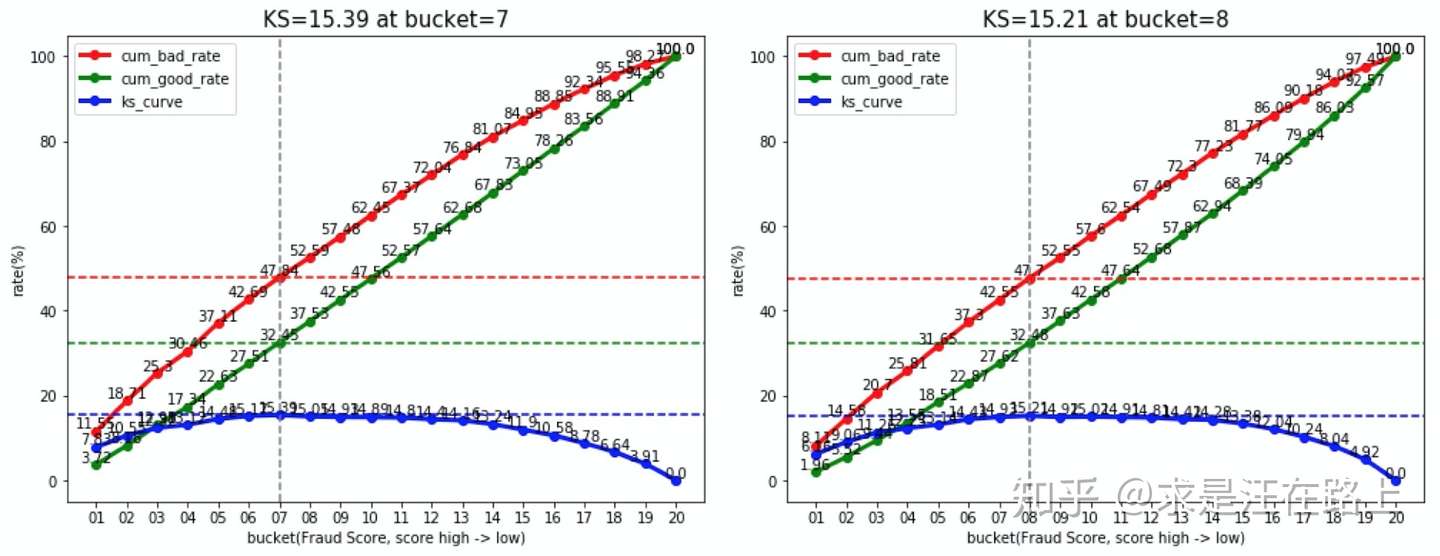
区分度(Discrimination) 业务:KS指标是风控建模同学最为追求的指标之一。通常情况下,KS越大,模型性能越好。但更需要分析KS不佳的原因,可结合ROC曲线进行辅助分析。
指标:Gini、AUC、KS。可参考《区分度评估指标(KS)深入理解应用 》
img
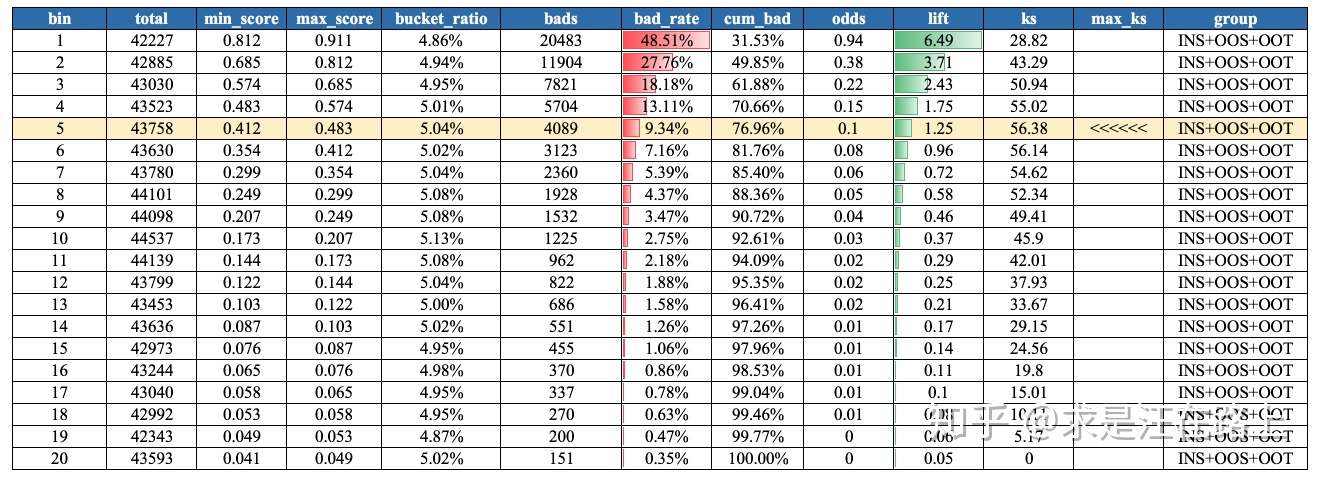
1.5.3 排序性(Ranking) 业务 :大部分模型在最终应用时只是利用到排序性,其主要是为了观察曲线的斜率。如图21所示的模型,排序性非常好,前5个分箱就能抓住大约77%的坏客户。
指标:按自然月/样本集维度,统计包含bad_rate、lift、odds等指标的Gain
Table。
lift = 召回样本的bad rate / 全部样本的bad rate
odds = bads / good
示例:模型分数Gain-Table
img
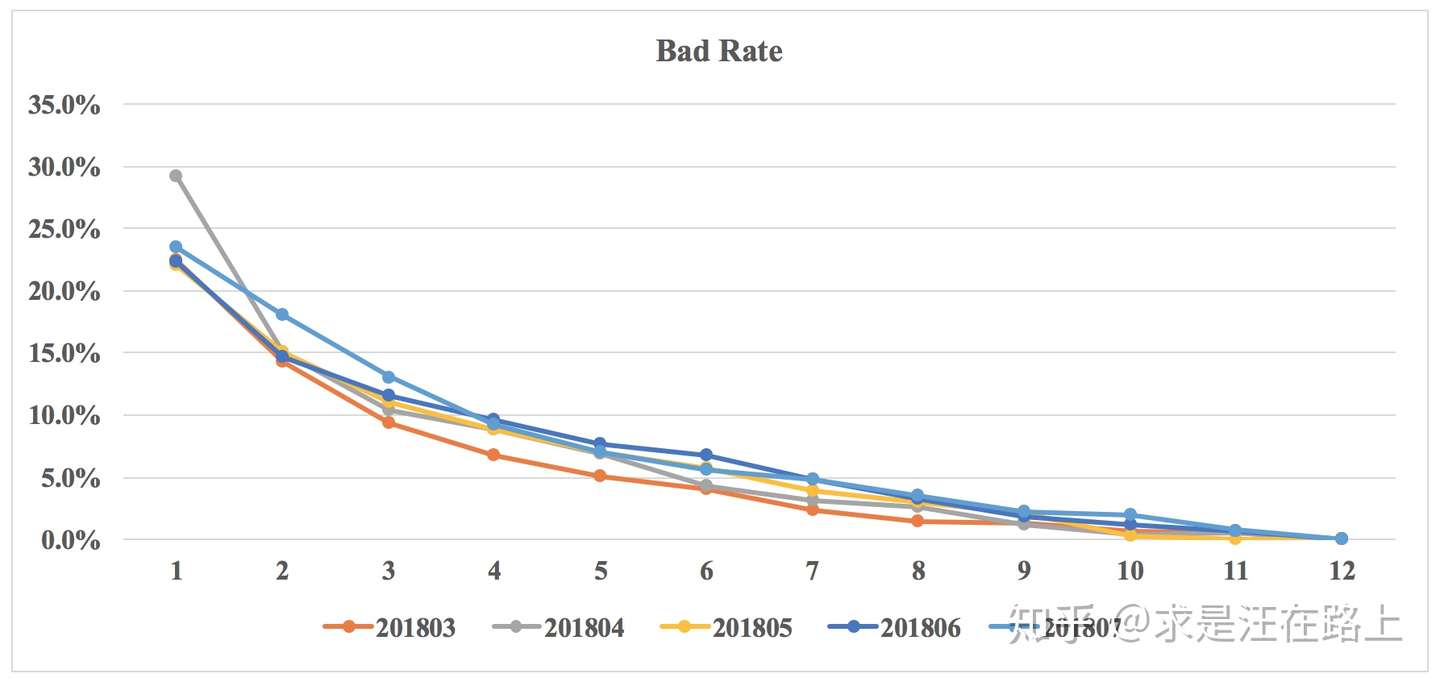
1.5.4 拟合度(Goodness of
Fit) 业务 :我们以训练集为基准,将模型分数划分成10个(或20个)分箱后,查看每个分箱里的reject
rate等指标是否一致。理论上,如果按每个Vintage绘制多条曲线,这些曲线会几乎重合,也就是围绕在训练集附近波动。此时,我们就可以相信模型在每一档的坏账估计比较准确。
指标:按自然月/样本集,评估每个分箱里lift、reject rate、bad
rate的点估计
示例:
img
1.6 开源的风控建模工具包简介 前文主要介绍一些理论,接下来介绍目前一些开源的风控建模工具包。
feature-selector scorecardpy toad
1.6.1 feature-selector
https://github.com/WillKoehrsen/feature-selector
主要功能:包括缺失率、单一值、相关性、特征重要性等。
Missing Values
Single Unique Values
Collinear Features
Zero Importance Features
Low Importance Features
1.6.2 scorecardpy
https://github.com/shichenxie/scorecardpy
主要功能:包括数据集划分、变量筛选、WOE分箱变换、评分卡尺度变换、模型性能评估。
data partition (split_df)
variable selection (iv, var_filter)
weight of evidence (woe) binning (woebin, woebin_plot, woebin_adj,
woebin_ply)
scorecard scaling (scorecard, scorecard_ply)
performance evaluation (perf_eva, perf_psi)
1.6.3 toad
https://toad.readthedocs.io/en/stable/tutorial_chinese.html
主要功能:包括数据分析处理、特征筛选、模型筛选、模型评估、评分卡尺度变换等。
data handling
feature selection and WOE binning
model selection
results evaluation and model validation
scorecard transformation.


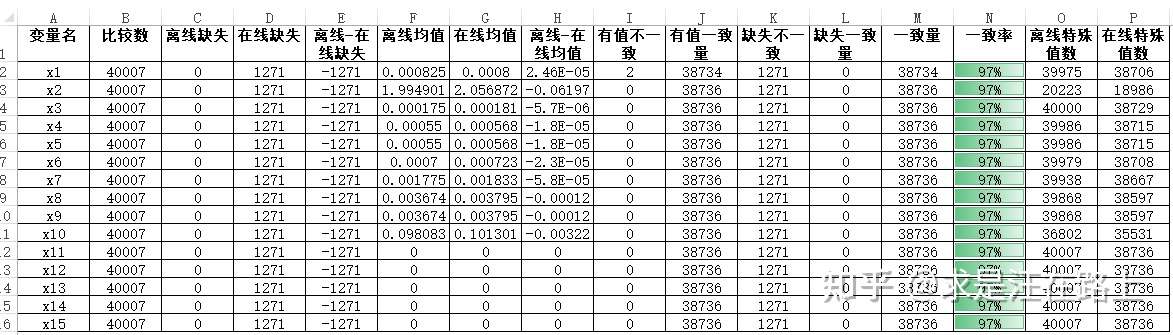



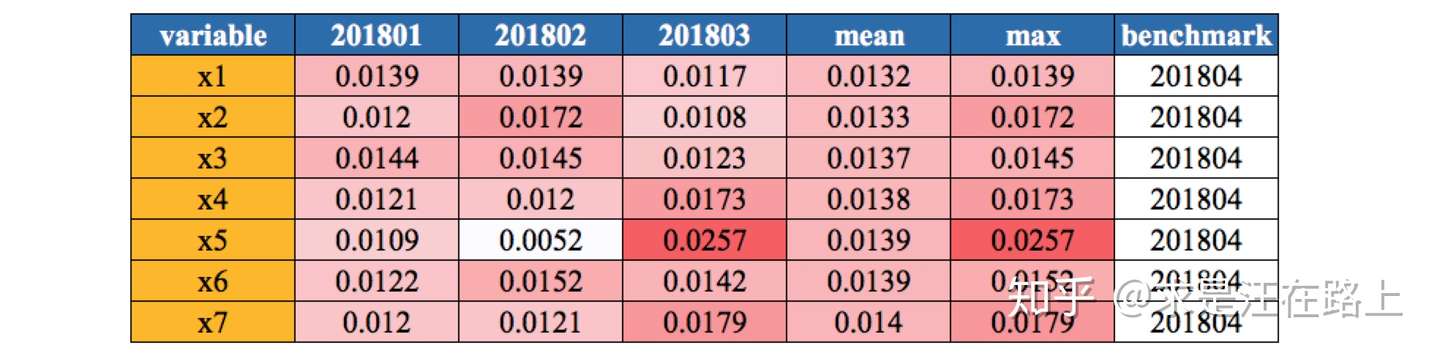


 模型分数PSI计算结果表(申请+放贷)
模型分数PSI计算结果表(申请+放贷)