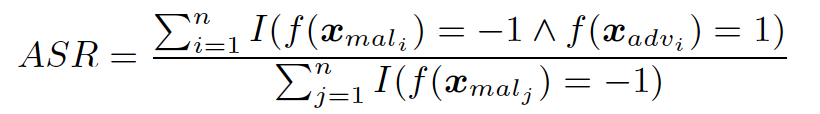AI安全（3）A survey on practical adversarial examples for malware classifiers

发表于 2021-07-29 更新于 2023-04-21 分类于【draft】应用，学术前沿，网络安全， AI安全本文字数： 17k 阅读时长 ≈ 30 分钟

恶意软件的对抗样本综述：

A survey on practical adversarial examples for malware classifiers

INTRODUCTION
BACKGROUND
- Machine learning for malware
- Adversarial examples
PRACTICAL ATTACKS
- Gradient-driven approaches
  - Editing bytes and metadata
  - Code transformations
- Problem-driven approaches
  - Editing bytes and metadata
  - Code transformations
DISCUSSION
- Challenges
  - Threat models
  - Establishing baselines
- Possible research directions
  - Defending against practical adversarial malware examples
  - Relationships between obfuscation and adversarial examples
  - Integration of static and dynamic analysis techniques
- Other Survey and systematization of knowledge papers
CONCLUSION
ACKNOWLEDGMENTS

ABSTRACT

基于机器学习的解决方案非常有助于解决处理大量数据的问题，例如恶意软件检测和分类。然而，人们发现，深层神经网络容易受到敌对示例的攻击，或故意干扰输入以导致错误标签的攻击。研究人员已经表明，可以利用此漏洞创建规避恶意软件样本。然而，许多提议的攻击并不生成可执行文件，而是生成特征向量。为了充分了解敌对示例对恶意软件检测的影响，我们回顾了针对生成可执行敌对恶意软件示例的恶意软件分类器的实际攻击。我们还讨论了该研究领域当前面临的挑战，以及改进建议和未来研究方向。

1 INTRODUCTION

基于机器学习的解决方案非常有助于解决处理大量数据的问题，例如恶意软件检测和分类。然而，人们发现，深层神经网络容易受到敌对示例的攻击，或故意干扰输入以导致错误标签的攻击。研究人员已经表明，可以利用此漏洞创建规避恶意软件样本。然而，许多提议的攻击并不生成可执行文件，而是生成特征向量。为了充分了解敌对示例对恶意软件检测的影响，我们回顾了针对生成可执行敌对恶意软件示例的恶意软件分类器的实际攻击。我们还讨论了该研究领域当前面临的挑战，以及改进建议和未来研究方向。

然而，在2014年，Szegedy等人表明深层神经网络（DNN）容易受到对抗性攻击。Grosse等人进一步证明，这种漏洞也适用于基于机器学习的恶意软件检测器和分类器[29]。自这项工作以来，针对流行的基于机器学习的模型（如MalConv[62]）开发了许多攻击，但其中许多攻击并不实用。具体地说，许多攻击不会生成实际的恶意软件，而是生成一个特征向量，表示可能受干扰的恶意文件应该是什么样子以逃避检测。由于逆特征映射的困难，在给定特征向量的情况下生成可执行程序是不切实际的[59]。也就是说，特征提取过程不是唯一可逆的，也不能保证找到的解决方案将包含与原始恶意软件样本相同的程序逻辑。在这项工作中，我们回顾了针对基于机器学习的恶意软件分类器和检测器的实际攻击，或者针对这些导致可执行恶意软件的ML模型的攻击。在第2节中，我们介绍并定义了对抗性示例以及考虑这些示例的威胁模型。然后，我们在第3节回顾了恶意软件领域的实际对抗性示例研究。我们为该领域的未来方向提供建议，并在第4节讨论任何挑战。最后，我们在第5节总结。

2 BACKGROUND

2.1 Machine learning for malware

检测恶意软件的经典方法是提取在受感染系统上发现的恶意样本的文件签名，并将其添加到签名数据库，也称为基于签名的检测[51]。对于这种方法，必须在整个样本以及相关样本的子集中搜索已知签名，因为恶意行为可以嵌入并交织在其他良性软件中。然而，由于基于特征码的检测依赖于捕获恶意软件样本，然后对其进行分析以生成新的特征码，因此它只能防御已知的攻击，并且只能尝试防御新的或模糊的恶意软件[67]。

基于机器学习的方法被提出作为这个问题的解决方案，因为它们能够预测新输入的标签。机器学习模型，如支持向量机（SVM）和均值聚类，用于恶意软件分类、检测和分析方法。在分类问题中，我们尝试将恶意软件样本分离为预定义的恶意软件系列。基于学习的模型基于由标记恶意软件样本组成的训练数据，推断新恶意软件样本的分类。检测问题可以看作是分类的一个子问题。对于检测，基于学习的模型用于在给定恶意和良性可执行文件时查找或检测恶意软件样本。由于检测是二进制分类的一种情况，基于学习的检测模型也可以称为分类器。分类和检测是训练数据标记时的监督算法。机器学习也可用于增强恶意软件分析。非监督聚类算法可用于学习恶意软件样本之间的新相似性[32]。此外，我们可以对基于学习的模型进行推理，以更好地理解恶意软件的恶意原因[7,20]。最近，随着深入学习方法研究的增加，研究人员开始利用卷积神经网络来分类和检测恶意软件[52,62]。

2.1.1 Static Features

N-gram是目前流行的用于恶意软件分类和检测的功能。Kolter和Maloof提出使用各种机器学习模型，包括朴素贝叶斯分类器、决策树、支持向量机（SVM）和增强模型[37]，从PE恶意软件中提取最相关的=-克字节码进行分类。他们发现，除了分类之外，他们的模型还可以用于恶意软件检测.

McBoost是作为一种在搜索恶意软件时快速分析大量二进制文件的工具引入的，并采用了三步流程[58]。第一步是使用基于启发式的分类器和两个不同的基于n-gram的分类器的集合来检测打包器。如果检测到封隔器，则使用QEMU和动态分析对二进制文件进行解包。最后，使用一个单独的n-gram分类器来检测应该转发以进行额外分析的恶意软件。

Santos等人在2009年提出使用=-grams作为基于文件签名的方法的替代方案。在这样做的过程中，他们表明机器学习，特别是k近邻模型和=-grams可以成功地用于检测新的恶意软件样本[67]#-grams还与动态特征一起使用，以同时合并恶意软件的多个视图，而无需实际进行动态分析[5]。最近的工作，如为Kaggle Microsoft恶意软件挑战提出的解决方案[64，78]，证明了字节和操作码=-grams的持续使用，分类准确率几乎为100%。

与使用操作码序列生成=gram类似，可以从程序的操作码跟踪中提取马尔可夫链。这样的马尔可夫链使用唯一的操作码作为其状态，并显示从一个操作码到另一个操作代码的转换概率。Anderson等人使用程序的马尔可夫链之间的相似性作为恶意软件检测的一个特征。类似地，Runwal等人[53]提出使用马尔可夫链之间的图相似性来检测嵌入式恶意软件，Shafiq等人[45]提出使用马尔科夫链来测量熵来检测恶意软件。

Jang等人介绍了BitShred，一种用于恶意软件分类和分析的工具[32]。BitShred使用位置敏感哈希对从样本中提取的=gram指纹进行哈希，以降低特征空间的维数。在k近邻模型中使用散列来对恶意软件样本进行聚类。此外，作者还表明BitShred可以用于改进以前的恶意软件检测和分类模型。例如，作者表明BitShred可以用于散列动态特征，例如Bayer等人[12]中生成的行为简档，以降低特征空间的维数。

Drebin对Android软件进行大规模静态分析，以提取硬件使用和请求、权限、API调用和网络信息等功能[7]。这些特征用于通过生成二进制指示符向量将样本映射到联合向量空间。这些二进制指示符向量被用作SVM的输入，SVM将样本标记为良性或恶意。重要的是，Drebin利用其模型的简单性，将模型的决策归因于特定的特征。这使得Drebin比基于复杂架构（如卷积神经网络）的恶意软件分类器和检测器更容易解释。

【ember、+ 字节直方图】

【恶意软件图像】Nataraj等人提出使用恶意软件图像（二进制文件的黑白图像表示）来检测恶意软件[52]。从那时起，研究人员和商业杀毒软件都使用恶意软件图像来高精度检测恶意软件[23，26，78]。Nataraj等人使用恶意软件图像创建了一个特征向量，该向量将用作支持向量机的输入。然而，最近的工作也表明，使用原始图像作为卷积神经网络的输入是有效的[23，34，38，82]。

【CFG控制流图】在开发静态功能方面也进行了研究，这些功能可以使用控制流图深入了解程序在运行时的行为。这项研究主要围绕构建控制流图和使用图匹配技术来检测恶意软件[13，16]。Ma等人在使用控制流图时采取了类似的方法，但提取了一系列API调用，试图模拟动态分析[46]。

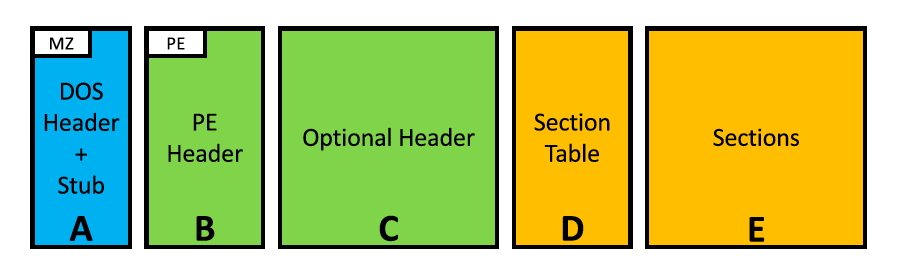
【Malconv】Raff等人采用了一种不同的方法，并提出了一种卷积神经网络（CNN）模型，该模型将整个二进制作为输入[62]。特别地，所提出的模型MalConv查看文件的原始字节以确定恶意。MalConv借鉴了神经网络的研究，从长序列中学习更高级别的表示，并依赖于CNN捕捉高级别局部不变量的能力。MalConv通过提取文件的：字节来工作。这些：用0G5字节填充字节，以创建大小为3的特征向量。如果：>3，则使用文件的前3个字节，而不使用任何额外的填充。通过与CNN联合学习的嵌入，将这个3长度的向量映射到固定长度的特征向量。

2.1.2 Dynamic Features

动态分析是一种通过在实时环境中运行二进制文件来分析二进制文件的技术。此环境通常是一个安全的沙盒或测试环境，如CWSandbox[80]和cuckoo sandbox[1]，以确保主机的安全。通常，这些环境都经过大量检测，以便记录已执行和加载的代码以及对内部文件、目录和设置所做的任何更改。这些记录的特征称为动态特征。

提取动态特征的最常用方法是记录系统和API调用的频率和顺序[3,21]。例如，Accessminer在动态分析期间记录系统调用trace，并生成每个样本的n-grams表示[42]。Accessminer将一个样本标记为恶意软件，如果该样本相对于某个预定义阈值包含多个“恶意”=-grams实例。动态分析的另一个好处是可以捕获和分析网络流量和通信，如Taintdroid[22]所述。这些功能还可用于为其他功能生成不同的恶意软件表示，或降低维数。

Bailey等人提出了一种用于恶意软件自动分类和分析的动态分析工具，该工具使用动态分析来记录生成的新进程、修改的任何文件、修改的任何注册表项以及网络访问和使用情况[11]。这些记录的特征用于创建amalware指纹，该指纹关注的是状态变化，而不是代码序列。这些动态特征用于使用标准化压缩距离度量创建恶意软件样本的层次聚类。

Rieck等人使用CWSandbox进行动态分析，类似于Bailey等人的工作，但是，使用字符串从结果文本报告中提取特征[63]。字符串频率与SVMto一起用于分类恶意软件样本。作者还表明，他们的方法可以通过引入新的“未知”类而扩展到恶意软件检测，而无需在训练集中引入良性样本。

拜耳等人通过使用污染分析来了解可执行文件如何使用来自操作系统的信息，从而扩展了之前的工作[12]。此外，所提出的方法使用操作系统对象和操作的抽象来创建行为概要。作者认为，由于能够在没有虚假系统调用的情况下对程序进行抽象或推理，因此抽象对规避更具鲁棒性。然后，将提取的行为特征与基于位置敏感哈希的聚类算法结合使用，对恶意软件样本进行分类。

程序的行为也可以建模为图，如Kolbitsch等人的工作[35]。作者扩展了malspec[18]，并使用systemcalls生成了程序的行为图。每个行为图都是一个有向无环图，其中节点是系统调用，有向边表示信息流。使用图匹配和相似性度量对已知恶意软件样本进行检测。

2.2 Adversarial examples

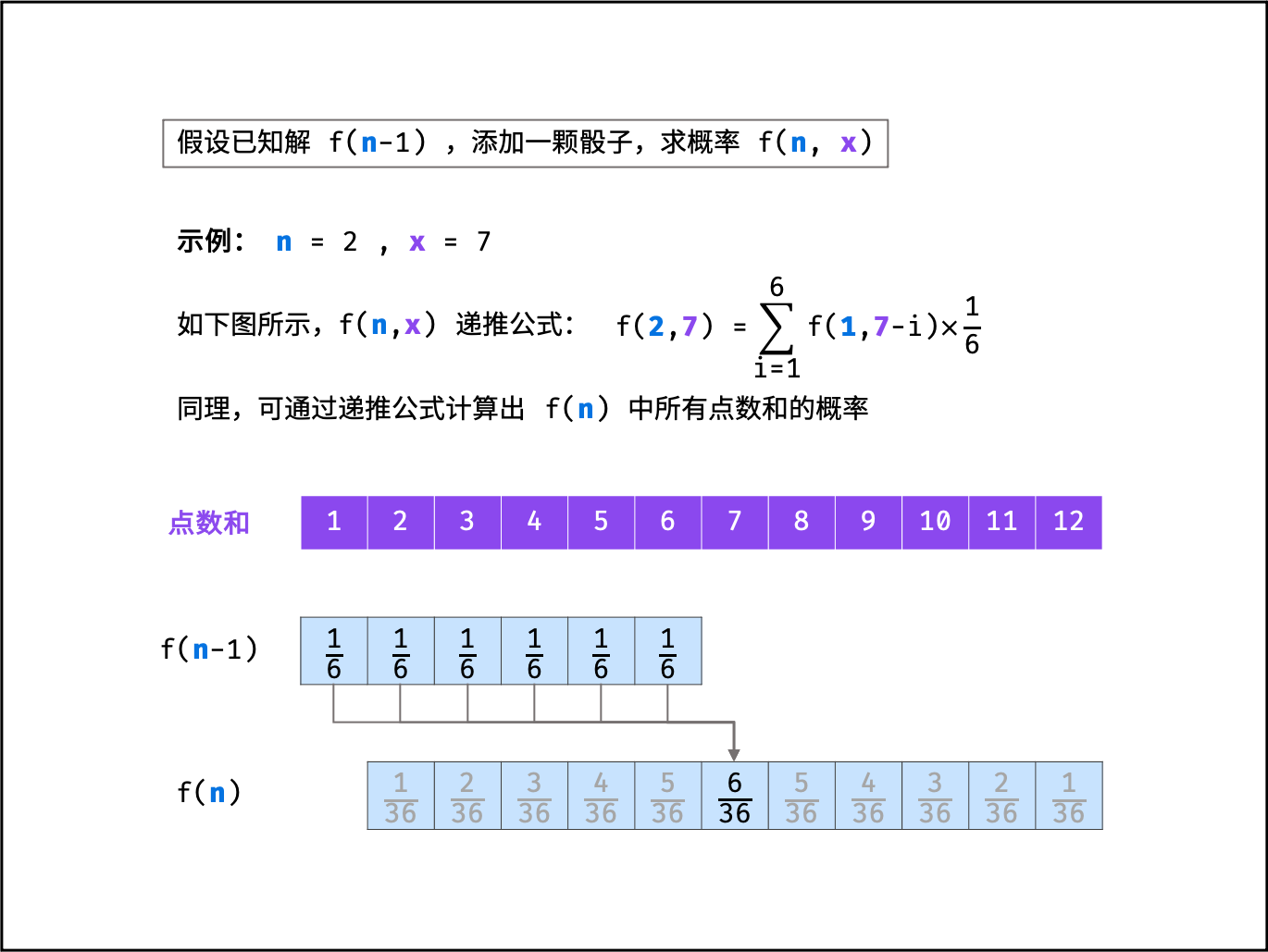
定义->图片等领域的限制条件->常用方法介绍->

在[72]中首次引入了对抗性示例的概念，并在[28]中进行了扩展。假设5是敌方计划攻击的目标分类器。这个分类器可以表示为一个函数$f(x)$，它接受一个输入并给它分配一个标签。通过用X扰动原始输入f生成对抗性示例x′5，使5（G）≠ 5（G′）。

有很多方法可以找到X，最流行的是快速梯度符号法[28]和卡里尼·瓦格纳（C&W）攻击[15]用于白盒模型，而替代模型攻击[55]用于黑盒模型。大多数攻击都会使用损失函数相对于输入的梯度来找到输入必须扰动的方向，以使输出发生想要的变化。然后使用该方向来查找X。我们在附录中简要讨论了这些攻击和其他攻击。

2.2.1 Threat models.

威胁模型是研究中对攻击者能力和已知信息的明确定义。在本节中，我们定义了机器学习领域中广泛使用的白盒和黑盒威胁模型。威胁模型由三部分组成：威胁向量和威胁面、知识和能力。

威胁向量和威胁面：威胁向量和威胁面表示攻击者与目标模型交互的方式。威胁向量是攻击者可以用来攻击模型的允许输入空间和位置。威胁面或攻击面是所有此类威胁向量的集合。通常情况下，威胁向量和威胁面由机器学习模型的输入和输出组成。然而，攻击者进入这些表面的能力进一步受到其知识和能力的限制。

Knowledge:攻击者的知识表示我们假设对攻击者了解目标模型的内容。然后，攻击者利用这些知识构建并发起攻击。在对抗式机器学习中，可以将攻击者的知识概括为白盒和黑盒模型。在白盒模型中，假设攻击者对系统有完全的了解。因此，我们假设攻击者可以完全访问目标机器学习模型（带有权重和参数）以及用于训练模型的数据。在黑箱模型中，假设攻击者只能访问模型的输入和输出。因此，攻击者不知道模型的内部或训练过程（例如，从可执行文件和梯度信息中提取的特征）。攻击者也可以建模为灰盒模型。在灰箱模型中，攻击者可以访问模型的输入、输出和一些其他信息（模型使用的特征）等。

本研究中回顾的作品与攻击者的知识并不完全一致。具体地说，有些作品可能假设攻击者还可以访问恶意软件源代码，而其他作品则没有。在第3节中，将明确指出每部作品与对抗性知识的一般定义之间的偏差

能力：攻击者的能力表示我们假设对攻击者可以发动的攻击类型。在对抗样本中，我们可以指定攻击者将使用的攻击算法。在恶意软件领域的对抗性示例中，攻击者的能力受到其知识的限制。例如，通过访问恶意软件源代码，攻击者可以轻松地在编译时应用特定的转换。但是，如果没有源代码，这将变得更加困难。

2.2.2 Adversarial malware examples

大多数对抗性示例研究是使用自然图像数据集进行的，如MNIST、CIFAR10和ImageNet。然而，有必要考虑一组允许干扰攻击者恶意软件实例功能的允许扰动。

对于自然图像，像素值会受到干扰以生成一个对抗性示例。只要得到的像素值在0到255之间，像素值的任何负数或正数变化都会导致图像发生轻微变化。可执行程序可以用类似的方式表示。根据定义，二进制文件的每个字节都在0x00和0xff之间。每个字节的十六进制表示可以转换为其十进制等效值（0到255之间）。在此状态下，可以使用相同的方法扰动字节和像素。然而，对字节的任意扰动可能不会产生有效的可执行文件，因为可执行程序存在于离散空间中。考虑改变可执行文件的一个字节的简单情况。如果字节来自ELF的.text部分，则新修改的字节可能会通过更改函数参数或导致错误指令而中断程序的功能。因此，将对抗性示例技术应用于恶意软件领域需要特别注意二进制文件的构造。最重要的是，对抗性恶意软件示例必须包含与原始恶意程序相同的恶意程序逻辑和功能。

对抗性恶意软件示例是一种直接的威胁，因为它们是规避性的恶意可执行文件，可以利用许多商业防病毒软件对混淆和变异的持久漏洞[61]。这将实际的恶意软件示例与恶意特征向量区分开来。虽然恶意特征向量也可以逃避检测或分类，但没有直接威胁。Pierazzi等人认为，在给定敌对特征向量的情况下生成可执行文件是困难的，并将其称为反向特征映射问题。逆特征映射问题没有唯一的解决方案。在n-gram分类器的简单情况下，可以通过多种方式添加n-gram。但是，它们并不能保证产生与原始恶意软件样本包含相同程序逻辑或可执行性的可执行文件。当处理黑盒模型时，这个问题变得更加困难，因为攻击者不知道分类器的输入和内部结构。Pierazzi等人解释说，实际的恶意软件示例有两种方法可以避免这种情况：

（1）一种梯度驱动方法，其中代码扰动对梯度的影响是近似的，并用于遵循梯度的方向；

（2）一种问题驱动方法，其中突变首先随机应用，然后再开始一种进化的方法。

3 PRACTICAL ATTACKS

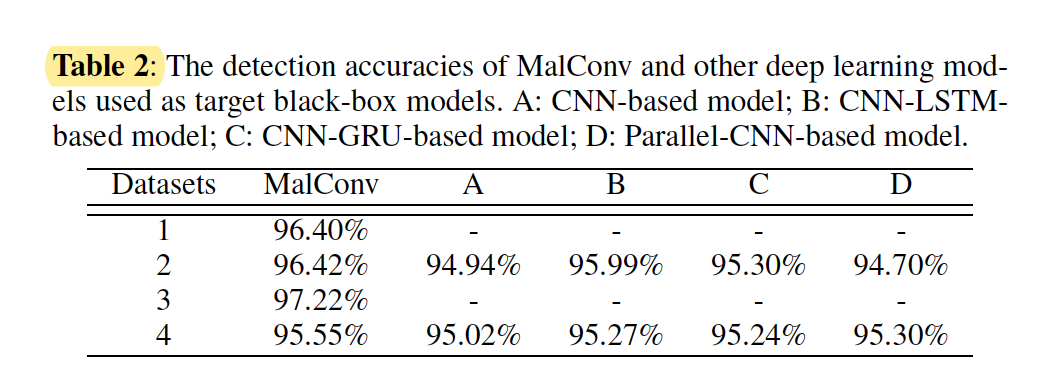
在本节中，我们将回顾对抗性恶意软件示例文献中的实际攻击，或导致可执行二进制文件的攻击。在表3中，我们概述了本工作中的实际攻击记录（1）如果工作是针对使用静态功能的恶意软件分类器评估的（2）如果工作是针对使用动态功能的恶意软件分类器评估的，（3）评估中的targetmodels，（4）攻击中的可用转换，（5）该方法是梯度驱动还是问题驱动。

我们使用[59]中的术语，并按照第2.2.2节中定义的梯度驱动和问题驱动方法组织我们的审查。对于这两种方法，我们进一步将文献组织为第3.1.1和3.2.1节中主要编辑字节和元数据的攻击，以及第3.1.2和3.2.2节中利用代码转换的攻击。

3.1 Gradient-driven approaches

3.1.1 Editing bytes and metadata

创建实际恶意软件示例的一种流行方法是在二进制文件中的未使用空间中添加或更改字节。此外，这可以在头中完成，以在不影响功能的情况下更改头元数据。在本节中，我们将回顾使用这种类型转换的拟议攻击。因为这些攻击集中在未使用或“不重要”（用于执行）字节上，所以它们不需要源代码来生成规避恶意软件样本。然而，除了GADGET[65]之外，这些攻击仍然是白盒攻击，因为它们需要完全访问目标模型来计算梯度。

##### [65] Generic Black-Box End-to-End Attack Against State of the Art API Call Based Malware Classifiers

2018年，Rosenberg等人提出了GADGET，这是一个利用DNN之间对抗样本的可转移性将PE恶意软件转化为规避变体的软件框架[65]。提议的攻击假设一个黑盒威胁模型，无法访问恶意软件源代码。但是，攻击假设目标模型将一系列API调用作为输入。为了生成对抗性示例，GADGET构建了一个代理或替代模型，该模型使用Papernot等人提出的基于Jacobian的数据集扩充进行训练，作为对自然图像分类器的攻击[55]。数据集扩充创建合成输入，帮助替代模型更好地逼近目标黑盒模型的决策边界。这增加了攻击可转移性的概率，因为替代模型和目标模型都将学习到类似的分布。一旦替代模型得到训练，通过向原始恶意软件的API调用序列添加虚拟API调用，生成对抗性恶意软件示例。作者将这些伪API调用称为语义NOP作为所选的API调用，或者它们相应的参数对原始程序逻辑没有影响。需要注意的是，作者只添加API调用，因为删除API调用可能会破坏程序的功能。

算法介绍：假设原始API调用序列是一个数组F0，其中每个索引都是9∈ [0，=]包含一个API调用。此过程的每个迭代8都返回一个新数组F8。在迭代8中，一个API调用3被添加到F8中−1在某个指数9处，将其推向梯度指示的方向，该梯度对替代模型的决策影响最大。这将导致F8，其中F8[9]=3和F8[9+1::]=F8−1[9:]因为索引9之后的前一序列中的所有API调用基本上都是“向后推”的。

这种通过添加伪API调用来干扰输入的方法确保了功能不会被破坏。为了从这个对抗性API调用序列生成实际的可执行文件，GADGET实现了一个钩住所有API调用的包装器。钩子根据需要从敌对API调用序列调用原始API和虚拟API。这些钩子确保生成的敌对恶意软件示例在某种意义上保持原始样本的功能和行为。GADGET根据定制模型进行评估，包括logistic回归、递归神经网络（RNN）、全连接深度神经网络（DNN）、卷积神经网络（CNN）、支持向量机、增强决策树和随机森林分类器。作者还表明，他们的攻击产生的恶意软件能够避开使用静态特征（如可打印字符串）的分类器。

[36] Adversarial Malware Binaries: Evading Deep Learning for Malware Detection in Executables

Kolosnjaji等人提出了一种针对MalConv的白盒攻击，该攻击通过迭代操作文件末尾的填充字节来生成对抗性PE恶意软件示例[36]。尽管作者指出PE中任何位置的字节都可以更改，但它需要对文件体系结构的精确了解，因为简单的更改可能会破坏文件完整性。因此，提议的攻击只关注字节附加。作者面临的一个挑战是由于其嵌入层，MALCONV的不可微性。为了避免这种情况，作者建议计算目标函数相对于嵌入表示I的梯度，而不是输入。每个填充字节都替换为最靠近第6行的嵌入式字节<（[）=I+[=其中=是标准化的渐变方向。但是，如果第6行（[）上的“<”投影未与=”对齐，则选择下一个最近的嵌入字节。通过仅更改文件末尾的填充，提议的攻击不会更改程序逻辑或原始almarware示例的功能。但是，这也限制了攻击允许的干扰总数。如第2节所述，MalConv从二进制文件中最多提取3个字节。如果二进制文件的大小小于3，则提取的：字节数为（3− :) 附加到它的0xff填充字节。这意味着提议的攻击受到原始恶意软件样本大小的限制。

[39] Deceiving End-to-End Deep Learning Malware Detectors using Adversarial Examples

Kruek等人[39]扩展了Kolosnjaji等人的工作，提出了一种方法，用于在敌对示例嵌入的情况下重建PE恶意软件样本。作者发现，从扰动嵌入重建字节∗ 像我一样经常是不平凡的∗ 可能会与我失去相似之处∈ / 用于学习“将填充字节映射到嵌入字节的函数。因此，他们提出了一种新的损失函数，以确保扰动嵌入∗ 将接近于实际的嵌入”。这是通过在生成的嵌入和“”之间的损失函数中引入距离项来实现的。

[20] Explaining Vulnerabilities of Deep Learning to Adversarial Malware Binaries

Demetrio等人提出将特征属性作为一种可解释的机器学习算法，以理解机器学习模型做出的决策[20]。特征归因基于Sundararajan等人于2017年引入的一种称为积分梯度的技术[71]。Demetrio等人观察了输入可执行文件的每个字节的属性，发现MalConv对二进制文件的PE头部分的权重很大。作者利用了这一漏洞，提出了针对MalConv的白盒攻击，该攻击只改变恶意软件样本头中的字节。此攻击使用了与[36]中相同的算法，但干扰了头中未使用和可编辑的字节，而不是在文件末尾填充。

3.1.2 Code transformations

上面的许多工作都指出，只要程序的功能和恶意行为没有改变，建议的方法就可以用来改变恶意二进制文件的.text部分。以下攻击利用模糊处理技术更改.text部分。

[57] Generation & Evaluation of Adversarial Examples for Malware Obfuscation.

Park等人提出了一种白盒攻击，该攻击利用语义NOP（如mov eax、x86汇编中的eax）来创建对抗性PE恶意软件示例[57]。作者攻击了使用可执行文件[52]的图像表示作为输入的卷积神经网络。可执行文件的图像表示将每个字节视为一个像素，并使用字节的十进制值作为像素值。攻击提出了两个步骤。首先，使用FGSM生成对抗性示例。此对抗性示例是一个映像，可能与原始恶意软件示例的功能或恶意行为不同。在第二步中，原始恶意软件样本和生成的敌对图像被用作动态规划算法的输入，该算法使用LLVM过程插入语义NOP。与[65]中添加API调用以类似于生成的对抗性特征向量的方式类似，动态规划算法添加了语义NOP，使得生成的恶意软件样本的图像表示类似于步骤1中生成的敌对图像。作者继续证明，由于敌对示例和干扰的可转移性，这种攻击可以用于黑盒模型[50， 55]. 使用一个简单的2层CNN作为替代模型，作者生成了对抗性恶意软件示例，这些示例也避开了黑盒模型，其中一个是使用字节级特征的梯度增强决策树。作者还提到，考虑到恶意软件的源代码，他们的攻击效果最好。然而，在缺乏源代码的情况下，可以使用二进制翻译和重写技术插入必要的语义NOP。需要注意的是，引入这些技术也会引入二进制提升过程中的工件。

3.2 Problem-driven approaches

在本节中，我们将回顾采用问题驱动方法的对抗性恶意软件示例算法。与第3.1节类似，我们使用攻击的可用转换进一步组织审查。问题驱动的方法不需要白盒访问梯度信息的目标。因此，以下方法是黑盒攻击。

3.2.1 Editing bytes and metadata

[6] Learning to Evade Static PE Machine Learning Malware Models via Reinforcement Learning
- Anderson

其中，Anderson等人提出了一个具有强化学习代理集[6]。RL代理因产生逃避检测的恶意软件的行为而获得奖励。通过这个游戏，代理学习创建规避恶意软件的策略。提议的攻击利用以下不会改变原始程序逻辑的操作：

向导入表中添加从未使用过的函数

更改节名

创建新的但未使用的部分

向节中未使用的空间添加字节

删除签名者信息

更改调试信息

打包或解包二进制文件

修改标题

使用这些操作，RL代理能够改变诸如PE元数据、人类可读字符串和字节直方图等特性。在培训阶段发生多达50000个突变后，RL代理根据梯度增强决策树模型进行评估，结果表明该模型能够成功地对恶意软件进行分类[78]。作者指出，他们的对抗性例子应该是功能性的。然而，他们发现，他们的攻击破坏了某些Windows PE的功能，这些PE使用了不太常见的文件格式或违反PE标准的混淆技巧。作者声称，通过确保二进制检测框架能够正确解析原始恶意软件样本，可以简单地解决这一问题。

[68] Automatic Generation of Adversarial Examples for Interpreting Malware Classifiers

Song等人在生成对抗性恶意软件示例时采用了不同的方法[68]。提议的攻击随机生成一系列宏操作，并将其应用于原始PE恶意软件样本。重复此操作，直到生成的转化恶意软件逃避检测。一旦恶意软件样本不可信，不必要的宏操作将从应用于其的宏操作序列中删除。这样做是为了最大限度地减少由于某些混淆技巧而意外破坏功能的可能性。剩余的宏操作随后被分解为微操作，以获得更详细的转换跟踪，从而生成恶意软件示例。我们建议读者阅读原始文章，以获得关于每个宏和微操作的更多详细信息，但是，我们在此简要描述它们。宏操作包括以下内容：

将字节追加到二进制文件的末尾

将字节追加到节末尾未使用的空间

增加一个新的部分重命名

注销已签名证书

删除调试信息

将标头中的校验和值归零

用语义等价的指令替换指令

其中一些宏操作可以分解为一系列较小的操作，称为微操作。例如，追加字节的操作可以分解为一次添加一个字节的序列。作者声称，通过分解每个宏操作，可以深入了解特定操作导致逃避的原因。提出的方法不是利用诸如FGSMor C&Wattack之类的对抗性示例生成算法，而是试图对机器学习模型提供一种更易于解释的攻击。该方法针对商业防病毒软件进行了评估，并被发现对包含静态和动态分析的分类器有效。

3.2.2 Code transformation

[83] Malware Detection in Adversarial Settings: Exploiting Feature Evolutions and Confusions in Android Apps.

Yang等人提出了两种对恶意软件样本的攻击，以逃避机器学习模型的检测，但没有使用机器学习算法[83]。建议的进化攻击不是针对错误分类，而是基于变异的上下文特征（由时间特征、区域设置特征和依赖性特征组成）模仿Android恶意软件的自然进化[84]。这是通过混淆工具OCTOPUS自动化这些变异策略并大规模使用它们来识别目标分类器上的“盲点”来实现的。恶意软件家族被组织成系统进化树[69]，以分析家族内的共同特征和不同特征。然后根据可行性和频率对每个特征变异进行排序，并进行排序。然后，顶级G突变用于生成新的恶意软件变体。作者还提出了一种特征混淆攻击来补充进化攻击。特征混淆攻击的目标是修改恶意软件样本，使某些特征与良性样本的特征相似。攻击开始于收集一组混乱的功能，或恶意软件和良性样本共享的一组功能。对于混淆特征集中的每个特征，记录包含该特征的良性和恶意样本数。如果存在更多良性样本，则该特征将添加到“目标特征”列表中。然后，攻击会变异恶意软件样本，使其包含已发现的目标特征，从而增加规避的可能性。针对基于Android学习的恶意软件分类器AppContext[84]和Drebin[7]对提出的方法进行了评估。需要注意的是，虽然攻击不需要白盒访问目标模型，但它确实假设（1）恶意软件源代码和（2）模型使用的功能知识。

[40] Deceiving Portable Executable Malware Classifiers into Targeted Misclassification with Practical Adversarial Examples

Kucuk等人认为，敌对恶意软件示例必须避开基于静态和动态机器学习的分类器[40]。因此，他们提出了一种针对PE恶意软件的攻击，利用虚假控制流混淆和API混淆来逃避使用静态和动态特征的模型的检测。应用的控制流混淆基于LLVM-Obfuscator[33]。LLVM模糊器通过使用不透明谓词和从不使用任意指令执行伪基本块，在LLVM-IR级别改变程序的控制流。使用差分分析，作者找到了最佳控制流混淆和伪基本块，以生成一个恶意软件示例。这会干扰静态特性，例如n-grams、操作码频率和导入的API调用。该攻击使用一种遗传算法来最小化所需目标类别的频率特征向量与恶意软件样本之间的Kullback-Leibler（KL）散度。为了规避基于动态API调用的恶意软件分类器，作者使用相同的遗传算法确定哪些API调用必须进行模糊处理，然后使用[70]中介绍的技术进行模糊处理。此外，再次使用相同的遗传算法确定应添加到原始恶意软件样本中的其他API调用序列，类似于[65]所采用的方法。

[59] Intriguing Properties of Adversarial ML Attacks in the Problem Space (2020 S&P)

Pierazzi等人提出了一种针对Android恶意软件分类器Drebin的黑盒攻击[59]。作者提出了一种问题空间方法，使用不透明谓词反复插入良性代码块，以改变Drebin提取的特征。这些良性代码块是在攻击之前通过分析训练集中的样本来初始化的，这些样本用于识别导致负面或良性标签的代码序列。攻击受到可行性检查的限制，以避免过度转换，从而增加怀疑。此外，使用FlowDroid[8]和So烟灰[75]插入代码块，以最小化副作用或伪影。

[24] HideNoSeek: Camouflaging Malicious JavaScript in Benign ASTs (2019 CCS)

HideNoSeek与其他应用代码转换的攻击不同，它试图通过将抽象语法树（AST）转换为良性来隐藏恶意JavaScript[24]。攻击开始于构建恶意和良性文件的AST，以检测两个类之间共享的子AST或子图。为了创建对抗性示例，HideNoSeek利用随机化、数据模糊和不透明结构插入良性子AST。该攻击还可以重写现有的AST，使其看起来是良性的。这些攻击是在黑盒模型中针对基于Zozzle的定制分类器进行的，Zozzle是一种使用从JavaScript AST中提取的特征的贝叶斯分类器[19]。

4 DISCUSSION

4.1 Challenges

首先，还应注意的是，我们绝不会减少或淡化恶意软件领域中不产生可执行恶意软件样本的对抗性示例研究的贡献。然而，我们认为，为了在现实的敌对环境中更好地构建提议的攻击，有必要扩展或包括关于扩展攻击以产生可执行恶意软件样本的可能方法的讨论。随着对抗性示例研究的快速发展，有必要充分了解这些攻击如何过渡到恶意软件检测和网络安全领域。全面开发或概念验证攻击也有助于开发针对敌对恶意软件样本的健壮模型。

4.1.1 Threat models

这一研究领域的一个挑战是威胁模型的不一致性。我们认为有必要明确定义每项研究中考虑的威胁模型，以便更好地理解攻击的局限性以及作者所做的任何假设。除了对抗性示例文献中使用的一般白盒和黑盒威胁模型外，我们建议包括（1）对源代码可用性的假设，以及（2）由于时间或计算限制对对手进行攻击的可行性。与Papernot等人[55]的工作类似，观察改变对手资源的效果会很有趣，例如，限制目标模型允许的查询数量，或为对手攻击的每次迭代产生成本。

4.1.2 Establishing baselines

另一个挑战是建立基线和基本真相。在整个审查的论文中，没有一致的数据集，也没有一致的（ML或商业）恶意软件分类器。尽管本次调查中考虑的所有作品都对顶级分类词有很高的漏检率，但我们无法公平地对它们进行评估。在提议的攻击和它们的实验评估之间保持一致将允许更好地比较攻击。然而，如[76]所示，维护一致的数据集和恶意软件分类器以及进行公平评估都会带来自身的挑战。这也将有助于扩展Quarta et.al.提出的评估，Quarta et.al.使用他们的框架crAVe表明，简单地混淆或变异恶意软件样本就足以逃避检测，因为并非所有反病毒软件都进行某种形式的动态分析。

4.1.3 Dataset

数据集：虽然将旧恶意软件转换为规避恶意软件确实显示了恶意软件检测中的漏洞，但排除较新的恶意软件样本会带来概念漂移(concept drift.)的风险。例如，如果恶意软件针对新平台进行了大幅更改，则旧的恶意软件数据集可能无法正确反映恶意功能和行为。良性程序样本也是如此。传统上，良性样本是从新安装的操作系统中刮取的。然而，目前尚不清楚这些预装程序是否反映了用户下载和/或扫描恶意行为的程序。

4.1.4 Malware classifiers

目前尚不清楚哪种恶意软件分类器最适合评估攻击。正如Song等人所说，假设模型的任何先验知识也是不现实的。我们认为目前没有也不会有一个一致的恶意软件检测模型基线，因为该领域的研究仍在增长。然而，我们建议未来的工作在黑盒威胁模型下评估他们对多分类器的攻击。这将有助于理解攻击在决策过程中使用不同特征的各种检测模型之间的可转移性。

4.2 Possible research directions

4.2.1 Defending against practical adversarial malware examples

一些研究已经在评估恶意软件领域中对抗性训练的使用[4,43]。然而，鲁棒机器学习研究包括许多其他防御策略，如平滑[2]和随机化[60]。目前尚不清楚这些方法是否会转移和防御对抗性恶意软件示例。

4.2.2 Relationships between obfuscation and adversarial examples

混淆和敌对示例有一个共同的目标：逃避检测。此外，大多数实用的对抗性恶意软件示例算法都将流行的混淆策略纳入了攻击中。一个可能的研究问题是评估使用更先进的模糊处理方法（如虚拟化）生成对抗性示例的可行性。目前还不清楚对抗性恶意软件示例与更传统的恶意软件规避技术（如Bulazel等人[14]中总结的技术）相比有什么好处。在Song等人[68]和Demetrio等人[20]的工作基础上扩展对抗性恶意软件示例的可解释性，并利用这一点进一步开发规避转换，这也是很有趣的。

4.2.3 Integration of static and dynamic analysis techniques

许多经过审查的工作都假设在测试之前没有对恶意软件样本进行高级分析。然而，情况并非总是如此。例如，预处理步骤可用于使用除臭框架（如SATURN[25]）对[57]和[40]产生的规避恶意软件样本进行除臭。未来的攻击和防御工作将考虑使用分类和检测管道，而不是单一的机器学习模型或商业防病毒产品，这将是一件有趣的事情。

4.3 Other Survey and systematization of knowledge papers

在本节中，我们将对涉及相关主题的知识论文进行其他调查和系统化。袁等人。深入学习的对抗性攻击和防御调查[86]。它们还提供了可以使用对抗性攻击的应用程序和问题域。与这项工作类似，Maiorca等人对基于机器学习的PDF恶意软件检测系统的对抗性攻击进行了调查[48]。Bulazel和Yener调查动态恶意软件分析规避和缓解策略[14]。Ye等人综述了数据挖掘技术在恶意软件检测中的应用[85]。Ucci等人利用机器学习对恶意软件分析进行了调查[74]。最后，van der Kuowe等人调查了为公平准确地评估安全性研究而必须考虑的常见基准测试缺陷。

5 CONCLUSION

我们对恶意软件领域中的实际对抗性示例进行了调查。随着基于机器学习的解决方案开始在工业界和学术界被采用，对抗性示例及其对网络安全领域的影响的研究非常重要。我们希望这项调查将为这一领域的未来研究提供有用的信息。

遗传算法

Robust Android Malware Detection against Adversarial Example Attacks. WWW 2021: 3603-3612
secml-malware: A Python Library for Adversarial Robustness Evaluation of Windows Malware Classifiers. CoRRabs/2104.12848 (2021)

AI安全（5）Functionality-Preserving Black-Box Optimization of Adversarial Windows Malware 2021 TIFS

发表于 2021-07-25 更新于 2023-04-21 分类于【draft】应用，学术前沿，网络安全， AI安全本文字数： 12k 阅读时长 ≈ 22 分钟

Functionality-Preserving Black-Box Optimization of Adversarial Windows Malware 2021 TIFS

keyword: 对抗样本；黑盒优化；

Abstract：

基于机器学习的Windows恶意软件检测器很容易受到攻击性示例的攻击，即使攻击者只获得对模型的黑盒查询访问权限。这些攻击的主要缺点是：查询效率低下，因为它们依赖于对输入恶意软件反复应用随机转换；它们可能还需要在优化过程的每次迭代中在沙盒中执行恶意软件，以确保其入侵功能得到保留。依赖于在恶意文件的末尾或在一些新创建的部分中注入良性内容（这些内容永远不会被执行）。我们的攻击被形式化为一个有约束的最小化问题，这也使得规避检测的概率和注入的有效负载的大小之间的权衡得到优化。对两种流行的静态Windows恶意软件检测器进行了实证研究，结果表明，即使只返回预测的标签，我们的黑盒攻击也可以通过很少的查询和较小的有效负载绕过它们。还评估了我们的攻击是否会转移到其他商业防病毒解决方案中，并意外地发现它们平均可以避开12个以上的商业防病毒引擎。讨论了我们的方法的局限性，以及它将来可能扩展到基于动态分析的目标恶意软件分类器。

一、Introduction

机器学习在计算机安全领域正变得越来越普遍。学术界和工业界都在投入时间、金钱和人力资源来应用这些统计技术来解决恶意软件检测的艰巨任务。特别是，Windows恶意软件仍然是一种威胁，因为每天都有成千上万的恶意程序被上传到VirusTotal^[1]。现代方法使用机器学习来大规模检测此类威胁，利用许多不同的学习算法和特征集^[1]–[7]。虽然这些技术已显示出很有前途的恶意软件检测能力，但它们最初的设计目的并不是为了处理攻击者可以操纵输入数据以逃避检测的非平稳、对抗性问题。

在过去的十年中，这一点在对抗式机器学习领域得到了广泛的证明^[8]，[9]。该研究领域研究了机器学习算法在训练或测试阶段受到攻击时的安全性问题。特别是，在基于学习的Windows恶意软件检测器的背景下，已经证明可以针对目标系统仔细优化对抗性恶意软件样本以绕过它^[10]–[17]。其中许多攻击都在黑盒设置中进行了演示，在黑盒设置中，攻击者只能对目标模型进行查询访问^[14]–[17]。这确实对作为云服务部署的此类系统的安全性提出了质疑，因为外部攻击者可以查询这些系统，然后根据目标系统提供的反馈优化其操作，直到实现规避。

然而，这些黑盒攻击在以下方面仍然不是非常有效：（i）所需查询的数量(reguired queries)，（i）其优化过程的复杂性(complexity)，以及（i）对输入样本执行的操作量(amount of manipulations)，如下所述: 1. 首先查询效率 is hindered by the fact that 攻击通过反复迭代并非专门针对逃避检测的转换（如在文件结尾后注入随机字节）来优化恶意软件。优化过程在计算上可能要求很高，因为有些攻击需要在每次迭代时在沙盒中执行敌对恶意软件样本，以确保其入侵功能得到保留。这种验证步骤是由在特征空间中操纵数据（而不是考虑可实现的输入修改^[18]的攻击所要求的或者考虑可能破坏恶意软件样本^[14]的功能的输入变换^[19]。 2. 虽然在沙盒中执行一次恶意软件样本可能不会显著减慢整个过程，但因为它需要在感染前的阶段恢复虚拟环境的状态。当优化过程的每次迭代后都必须重复此步骤时，问题就变得相关了。此外，许多恶意软件样本可以检测它们是否在虚拟环境中运行，并延迟执行以保持未被检测到：Malware dynamic analysis evasion techniques：A survey； 3. 所有这些攻击都通过显著操纵输入恶意软件的内容来实现规避，而不考虑额外的限制，例如，对生成的文件大小或注入的节数的限制。这可能导致攻击样本很容易被检测为异常，只需查看一些无关紧要的特征（trivial characteristics），如文件大小或节数。

在本文中，我们提出了一个新的黑盒攻击家族（Section 3）可以有效地优化恶意软件样本。首先，我们的攻击是高效查询的，因为它们依赖于注入特定目标的内容以便于规避，即从良性样本中提取（而不是随机生成）。第二，它们在设计上保留了功能，因为它们利用了一组操作，这些操作仅通过利用用于在磁盘上存储程序的文件格式的模糊性将内容注入恶意程序，而不改变其执行跟踪。虽然在这项工作中，我们只关注在文件末尾（填充）或在一些新创建的节（节注入）中注入内容，但我们的方法足够通用，可以包含更广泛的功能保留操作。最后，我们的攻击更加隐蔽。特别地，它们被形式化为一个约束最小化问题，该问题不仅优化了规避检测的概率，而且通过一个特定的正则化项（via a specific regularization term.）来惩罚注入的敌方有效载荷的大小。

二、PROGRAMS AND MALWARE DETECTION

在本节中，我们首先讨论Windows可移植可执行文件（PE）格式，2它描述了程序如何存储在磁盘上，并向操作系统（OS）解释了如何在执行之前将其加载到内存中。然后，我们将介绍这项工作剩余部分中使用的两种流行的基于学习的Windows恶意软件检测器。

2.1 The Windows Portable Executable (PE) File Format

Windows PE格式由几个组件组成，如图1所示，如下所述。DOS标题（A）。它包含用于在DOS环境中加载可执行文件的元数据，以及DOS存根，如果在DOS环境中执行，则会打印“此程序无法在DOS模式下运行”。保留这两个组件是为了保持与旧版Microsoft操作系统的兼容性。从现代应用程序的角度来看，DOS头中唯一相关的部分是：（i）幻数MZ，文件的两字节长签名，以及（ii）偏移量0x3c处的四字节长整数，用作指向实际头的指针。如果这两个值中的一个由于某种原因被置乱，则认为程序已损坏，操作系统将不会执行该程序。

PE header（B）。它包含幻数PE以及其他文件特征，如目标体系结构、头大小和文件属性。

Optional Header（C）。它包含操作系统初始化加载程序所需的信息。它还包含指向有用结构的偏移量，如操作系统解析依赖关系所需的导入地址表（IAT）和导出表偏移量，后者指示在何处查找其他程序可以引用的函数。截

Section Table（D）。它是一个条目列表，指示程序的每个核心组件的特征，以及OS加载程序应该在文件中找到它们的位置。

Sections（E）节。这些连续的字节块承载着可执行文件的真实内容。要列出一些：。文本包含代码。数据包含全局变量和。rdata包含只读常量和计数。

可执行程序的结构可用于静态推断有关其行为的信息。事实上，大多数防病毒供应商应用静态分析来检测野外威胁，而不在受控环境中执行可疑程序。这种方法节省了时间和资源，因为防病毒程序不会在主机操作系统内执行可疑软件。静态分析是第一道防线，其性能对于抵御野外无数威胁至关重要。

2.2 Learning-Based Windows Malware Detection

MalConv
EMBER

三、BLACK-BOX OPTIMIZATION OF ADVERSARIAL WINDOWS MALWARE

在本节中，我们将介绍一种新的黑盒攻击框架，命名为GAMMA（Genetic adricative Machine learning Malware attack）。GAMMA可以有效地优化敌方恶意软件样本，同时只需要黑盒访问模型，即只查询目标模型并观察其输出，而不访问其内部结构和参数。我们的攻击依赖于一组保留功能的操作，这些操作利用用于在磁盘上存储程序的PE格式的模糊性将内容注入恶意程序，而不改变其执行跟踪。这使我们能够摆脱需要计算的验证步骤，以确保被操纵的恶意软件保留其预期功能。特别是，我们认为这里的内容操纵，特别是针对有利于逃避，即，从良性样本中提取，而不是随机产生。虽然这使得我们的攻击更加有效，但值得注意的是，我们的框架足够通用，可以包含许多其他不同的内容操作技术。最后，为了使我们的攻击更加隐蔽，我们将其形式化为一个约束优化问题，该问题不仅最小化了逃避检测的概率，而且通过一个特定的惩罚项最小化了注入内容的大小。

符号定义，我们用x 2 x表示 f0；：：：；255g （恶意）输入程序，描述为任意长度的字节字符串。然后，我们定义了一组k个不同的保留功能的操作，这些操作可以作为向量s2 s应用于输入程序x [0；1]k

Notation: $x$ malicious；$s$ (k 种 vector);（良性初始注入+遗传算法）

3.1 Functionality-Preserving Manipulations（保留功能的操作）

我们在这里讨论一组可以在我们的攻击框架中使用的保留功能的操作。在windowspe文件格式的上下文中，只有一些转换可以在不影响输入程序执行的情况下应用。我们将其分为结构性和行为性两类，详情如下。

Structural结构化：这一系列操作只影响输入程序的结构，利用文件格式中的模糊性，而不改变其行为。
1. Perturb Header Fields：扰动标题字段[13]–[15]。此技术包括更改节名称、中断校验和以及更改调试信息。
2. Filling Slack Space：填充松弛空间[12]–[15]，[23]。此技术操纵编译器插入的空闲空间，以保持文件内部的对齐。相应的空闲字节（图1中的E内）通常被设置为零，并且它们从不被可执行文件的代码引用。
3. Padding：填充[11]、[12]、[23]。这种技术在文件末尾注入额外的字节（在图1中的E之后）。
4. Manipulating DOS Header and Stub：操作DOS头和存根[10]，[22]。这项技术修改了DOS头中一些现代程序不使用的字节。
5. Extend the DOS Header: 扩展DOS标头[22]。这种技术通过在程序的实际头之前注入内容来扩展DOS头。
6. Content shifting：内容转移[22]。这种技术通过向前移动内容，在节的开始之前创建额外的空间，并在中间注入对抗性内容。
7. Import Function Injection：导入函数注入[13]–[15]。该技术通过向导入地址表添加适当的条目来注入导入函数，指定在加载过程中必须包括哪个库中的哪个函数（这影响图1中的C和E）。
8. Section Injection：第[13]-[15]节。这种技术通过在节表中创建一个额外的条目将新的节注入到输入文件中（从而影响图1中的D和E）。每个节条目的长度为40字节，因此所有内容都必须按该长度进行移位，而不会影响头指定的文件和节对齐方式。
Behavioral行为：这一系列的干扰可以改变程序的行为和执行痕迹，但仍然保留恶意软件程序的预期功能。例如，这些转换包含[24]中的二进制重写技术，如下所述。

Packing：加壳[13]–[15]。软件加壳的原理是在原始程序外部添加一个保护层，以保护程序代码和数据不被恶意软件攻击者破解、篡改或复制。通过壳程序的加载和解码、原始程序的加密和解密、壳程序的动态反调试和反破解、以及代码混淆和虚拟机技术等手段，可以使程序更加安全和难以被攻击者破解。封隔器的作用是侵入性的，因为输入样本的整个结构都被修改了；
- [13] R. L. Castro, C. Schmitt, and G. D. Rodosek, “ARMED: How automaticmalware modifications can evade static detection?” in Proc. 5th Int.Conf. Inf. Manage. (ICIM), Mar. 2019, pp. 20–27.
- [14] R. L. Castro, C. Schmitt, and G. D. Rodosek, “Aimed: Evolving malwarewith genetic programming to evade detection,” in Proc. 18th Int. Conf.TrustCom, 2019, pp. 240–247.
- [15] H. S. Anderson, A. Kharkar, B. Filar, and P. Roth, “Evading machinelearning malware detection,” in Proc. BlackHat, 2017.
Direct：直接[24]。这种方法重写代码的特定部分，比如用等价的指令替换汇编指令（例如，用相反的符号进行加法和减法）。
- 这种技术被称为“代码混淆”（code obfuscation）。它是一种常见的恶意软件攻击技术，攻击者使用代码混淆技术来隐藏恶意代码的真实意图，使其更难以被检测和分析。
- 在这种技术中，攻击者会通过重写代码的特定部分来进行代码混淆。例如，攻击者可以用等价的指令替换汇编指令，或者用相反的符号进行加法和减法等操作。这样一来，原本的代码逻辑就被混淆了，使得恶意代码更难以被理解和分析。
- 代码混淆技术可以有效地防止恶意代码被检测和分析，因为它使得恶意代码的行为更难以被预测和理解。然而，代码混淆也会使得恶意代码更难以被清除和修复，因为恶意代码的行为可能会受到混淆代码的影响，从而导致误报和误判。
- [24] M. Wenzl, G. Merzdovnik, J. Ullrich, and E. Weippl, “From hackto elaborate technique—A survey on binary rewriting,” ACM Comput.Surv., vol. 52, no. 3, pp. 1–37, Jul. 2019
Minimal Invasive[15]，[24]。此技术将入口点设置为新的可执行部分，该部分跳回原始代码。
- 这种技术被称为“代码注入”（code injection）。它是一种恶意软件攻击技术，攻击者通过将恶意代码注入到受害者计算机中的合法进程中，来控制受害者计算机、窃取敏感信息或者执行其他恶意行为。
- 在这种技术中，攻击者会将恶意代码插入到被感染程序的可执行部分中，并将程序的入口点设置为恶意代码的起始位置，使程序在运行时首先执行恶意代码。然后，恶意代码会执行一些操作（如窃取信息、下载其他恶意代码等），最后将程序的控制权转回到原始代码中，以避免被检测到。
- 代码注入是一种常见的恶意软件攻击技术，攻击者可以使用多种方法来实现代码注入，如缓冲区溢出、API Hooking、DLL注入等。为了防止代码注入攻击，建议用户保持软件的更新和使用安全软件进行防护。
Full Translation：完整翻译[24]。这种方法将所有代码提升到更高的表示形式，例如LLVM，4，因为它简化了扰动的应用，然后将代码翻译回汇编语言。
- 这种技术被称为“语义混淆”（semantic obfuscation）。它是一种常见的恶意软件攻击技术，攻击者使用语义混淆技术来隐藏恶意代码的真实意图，使其更难以被检测和分析。
- 在这种技术中，攻击者会将所有代码提升到更高的表示形式，例如LLVM，因为这样可以简化扰动的应用。然后，攻击者会将代码翻译回汇编语言，但是这时的代码已经被语义混淆了，使得其更难以被理解和分析。
- 语义混淆技术可以有效地防止恶意代码被检测和分析，因为它使得恶意代码的行为更难以被预测和理解。然而，语义混淆也会使得恶意代码更难以被清除和修复，因为恶意代码的行为可能会受到混淆代码的影响，从而导致误报和误判。
Dropper[30]。这种方法将代码存储为另一个二进制文件的资源，然后在运行时加载。
- 这种技术被称为“二进制文件注入”（binary file injection）。它是一种恶意软件攻击技术，攻击者使用二进制文件注入技术来隐藏恶意代码，使其更难以被检测和分析。
- 在这种技术中，攻击者会将恶意代码存储为另一个二进制文件的资源，然后在运行时加载。这样一来，恶意代码就被隐藏在另一个二进制文件的资源中，使得它更难以被检测和分析。
- 二进制文件注入技术可以有效地防止恶意代码被检测和分析，因为它使得恶意代码更难以被发现。然而，二进制文件注入也会使得恶意代码更难以被清除和修复，因为恶意代码可能会被存储在多个文件中，从而需要进行全面的扫描和清除。
- [30] F. Ceschin, M. Botacin, H. M. Gomes, L. Oliveira, and A. Grégio,“Shallow security: On the creation of adversarial variants to evademachine learning-based malware detectors,” in Proc. 3rd ReversingOffensive-Oriented Trends Symp., 2019, pp. 1–9.

Padding and Section-Injection Attacks 填充和节注入攻击

虽然GAMMA可以通过在[33 ]中的开源实现支持大多数上述操作，但是我们只考虑在这项工作中的填充和分段注入攻击，因为它们提供了两个有代表性的示例，即在不需要操纵额外的头组件的情况下，在样本内注入内容（例如，节区表）。特别是，Padding将内容注入到可执行文件的未使用空间中，而不改变任何其他头组件。相反，Section infection不仅允许像其他技术一样注入自定义内容，而且还通过在节表中添加节条目来操纵可执行文件的结构。

四、实验

在本节中，我们根据经验评估了针对GBDT和MalConv恶意软件检测器的攻击的有效性。我们在一台装有Intel的工作站上进行了实验至强 CPU E5-2670，具有48个CPU和128 GB RAM。MalConv的预训练版本呈现出略有不同的体系结构w.r.t。原始公式：1 MB的输入大小和256的填充值，以避免移动预处理部分。该网络使用PyTorch实现【25】。我们使用DEAP开发了GAMMA的遗传优化器【26】。我们使用10个元素的总体大小N测试了攻击，将查询预算T从10更改为510。如果优化器在一个局部最小值上停滞了5次以上的迭代，我们将停止该过程。我们使用正则化参数的值 2层10 ig9i=3。由于攻击特征空间S在攻击者可能添加的节数上是参数化的，因此我们随机提取了75个。如第III-a节所述，我们的goodware数据集中的rdata部分将用于向输入恶意软件添加内容，最大容量为2.5 MB。我们愿意将此数字设置为高值，因为优化器将发现较小的有效负载，这要归功于行为为“1”标准的惩罚术语所施加的稀疏性。我们实现并公开了用于计算这些攻击的库，名为secml恶意软件。5.

4.1 无攻击时的性能

为了在没有攻击的情况下评估这两种分类器的性能，我们收集了一组分类器；15000良性和15；000个恶意软件样本。恶意软件样本是从VirusTotal收集的，而goodware样本是通过从GitHub下载可执行程序收集的。结果如图3所示。为GBDT选择的阈值为0.8336，对应于0.039的假阳性率（FPR）和0.95的真阳性率（TPR）。MalConv使用的阈值为0.5，这导致FPR为0.035，TPR为0.69。图中的红点直接在曲线上显示这些值。这些结果与GBDT【6】的作者给出的描述相当，因为两种检测器的w.r.t得分略低。这篇论文中报道了这一点。不过，它们都可以作为我们分析的基线。

4.2 攻击评估

我们从收集的15K恶意软件中随机抽取500个用于对抗性攻击，其中包括5.3%的勒索软件、29%的下载软件、18%的病毒、7%的后门软件、29%的灰色软件、8%的蠕虫，以及其他百分比较低的家族。图4显示了检测率和对抗性有效载荷大小如何随查询数量和正则化参数的值而变化。曲线图中的每条曲线都是通过计算每个值的平均检测率和平均大小生成的 , 针对发送的不同查询数重复此操作。作为的值由于在计算目标函数时，惩罚项可以忽略不计，因此该算法可以找到更多有效载荷较大的规避样本。另一方面，通过增加由此产生的攻击特征向量变得稀疏，生成更小但更可检测的对抗性示例。在这种情况下，惩罚项会吞噬分类器计算的分数，这在优化过程中变得无关紧要。另一个重要影响是遗传优化器使用的总查询数：发送的越多，敌对示例的检测率和大小越好。直观地说，通过发送更多的查询，GAMMA可以同时探索更多隐藏和回避的解决方案，但在优化过程的早期阶段无法找到此类解决方案。为了证明我们的方法的有效性，我们报告了应用递增长度随机字节序列的结果。这个实验强调了轻微的下降趋势，但使用良性内容注入的优化攻击比随机干扰更有效。分段注入攻击比填充攻击更能降低GBDT的检测率。由于第一种技术还在节表中引入了节条目，因此与填充攻击修改的特性相比，对抗性有效载荷干扰的特性更多。

4.3 硬标签攻击

我们在表I中显示了聚合结果，重点比较了软标签和硬标签攻击的性能。每个条目表示每个检测器的平均检测率和平均对抗有效负载大小，给定一对用于计算指定攻击的查询/正则化参数。我们计算了4个不同的在集合f10中（2i+1）g4i=1。结果表明，在没有置信度得分的情况下，一旦发现一个规避有效载荷，则无论正则化参数的值如何，其大小都会在遗传算法的一次又一次迭代中得到优化 . 这是由我们为实验设置的结果造成的：我们使用一个无限值来丢弃每个检测到的敌对示例，因此所有剩余的示例仅用于优化大小，作为优化的约束本身。我们的方法在这种环境中的有效性是由注入的内容的性质引起的，它模仿良性类，图4证实了这一点，其中注入随机字节序列对目标没有影响。相反，查询的数量本身起到了调节器的作用，因为太少的查询会导致更大的对抗性有效载荷，而置信度较低，而大量的查询会导致分数较高的小有效载荷。

4.4 时间分析

从时间的角度来看，GAMMA的复杂性主要取决于查询探测器所花费的时间。表II显示了计算每个攻击和目标的单个查询所需的平均运行时间。令人惊讶的是，特征提取阶段和GBDT预测所花费的时间之和小于神经网络处理所有字节所需的时间。

4.5 加壳影响

由于这些分类器仅利用静态特征，因此我们有理由问自己，在不应用第三节中介绍的所有技术的情况下，加密程序内容是否足以逃避检测。打包是一种通过应用压缩、加密或编码算法来减少可执行文件大小的技术。由于打包器的作用完全改变了磁盘上的程序表示，恶意软件供应商广泛使用打包器向分析师隐藏其产品，增加了逆向工程分析的难度。在这种情况下，我们将一种著名的技术UPX7应用于1000个恶意软件和1000个goodware程序，并测试MalConv和GBDT的规避率。UPX封隔器的有效性如图5所示。这两个检测器在打包样本时都会给出恶意分数，通过查看打包好的goodware程序的方框图，这是很直观的。这两种检测器都增加了它们对恶意软件类别的得分，而打包恶意软件的均值和方差只有很小的变化。

从这些结果来看，我们认为，探测器将包装技术的应用视为一种恶意特征。这可能是由于训练集中有大量打包的恶意软件，而不是缺少打包的好软件。因此，基于此类数据训练的模型可能会有偏差，使他们错误地认为样本是恶意的，只是因为它是打包的。此外，如果使用一种技术打包足够的样本，学习算法应该能够捕获打包程序中打包程序本身留下的签名。例如，UPX打包器创建两个名为UPX0和UPX1的可执行部分，其中包含提取代码和原始压缩程序。我们认为，通过包装技术进行规避更可能由看不见的包装商实现，即恶意软件供应商自己开发的定制解决方案。

We believe that evasion through packing techniques should more likely to be achieved by unseen packers, i.e. custom solutions developed by malware vendors themselves.

4.6 Evaluation on Antivirus Programs (VirusTotal)

我们在此评估我们的攻击对商用探测器的影响。在这种情况下，我们无意逃避这些商业程序的检测，例如打包输入样本，而是评估这些方法是否可以检测到我们的攻击，因为我们的攻击只对输入恶意软件样本的内容进行了最小程度的修改。特别是，我们应用于恶意软件样本的操作仅涉及每个程序的语法结构，我们的目的是评估此类转换的应用是否会对其他防病毒程序构成威胁。我们预计，大多数商业解决方案不应受到此类攻击的影响。我们依赖VirusTotal检索到的响应，8这是许多威胁检测器的在线接口。该服务提供了一个API，可以通过从远程上传样本来查询系统。我们通过在向样本中注入对抗性负载之前和之后发送200个恶意软件样本来测试我们的攻击性能，该样本使用针对GBDT分类器的分段注入攻击进行了优化。我们还将我们的攻击与基线随机攻击进行比较，基线随机攻击只是向每个样本添加50 KB的随机负载。表三显示了VirusTotal上托管的防病毒程序平均有多少（总共70个）检测到提交的恶意软件样本。虽然随机攻击只会略微减少每个样本的检测数量，但分段注入攻击能够绕过平均每个样本12个以上的检测器。为了更好地评估我们的攻击对单个杀毒程序的影响，在表IV中，我们报告了2019年Gartner端点保护平台幻方图上出现的9种不同杀毒产品的检测率，9包括许多领先和有远见的产品，在执行随机和部分注入攻击之前和之后。在许多情况下，我们的节注入攻击能够大幅降低检测率（参见，例如，AV1、AV3、AV7和AV9），显著优于随机攻击（参见，例如，AV1和AV9）。原因可能是，其中一些防病毒程序已经使用基于静态机器学习的检测器，在保护终端客户端免受恶意软件攻击时实施了第一道防线，这也在他们的博客或网站上得到了证实，这使他们更容易受到我们的攻击。综上所述，我们的分析强调，这些商业产品可以通过转移攻击来规避，我们相信，通过对其进行优化攻击，它们的检测率可能会下降更多。

五、RELATED WORK

强化学习[15]

Anderson等人[15]提出了一种强化学习方法，以确定导致逃避的最佳操作顺序。为了测试代理的有效性，他们还测试了随机选取的操作的应用。他们用作基线的模型是我们在这项工作中分析的GBDT分类器的原始版本，使用较少的样本进行训练。为了训练学习代理的策略，他们通过为可使用的查询数量确定预算，让模型探索对抗性示例的空间。用于培训这些策略的查询平均数量约为1600[15]。作者没有报告对抗性恶意软件产生的文件大小：强化学习方法包含放大磁盘上表示的操作，但不清楚如何和多少。不同的是，我们的方法不需要培训阶段，因为它可以针对远程探测器进行部署。我们使用的转换在设计上是功能不变的，它们的应用程序不会改变程序的执行流。最后，通过在优化过程中插入正则化器，我们考虑了有多少内容被添加到输入恶意软件中。通过这种方法，可以控制插入噪声的数量，并且该算法可以找到不仅避开目标分类器，而且在大小上受到限制的对抗性示例。

随机算法和遗传算法[13],[14]

Castro等人[13]，[14]应用随机算法和遗传算法来干扰输入恶意软件，并在沙箱中的优化过程的每次迭代中测试样本的功能。这些突变与Anderson等人提出的相同[15]。这些工作的作者表示，他们需要大约4分钟来创建敌对恶意软件，使用100个查询。尚未公布任何架构细节。我们不需要在沙箱中验证恶意软件，因为我们在变异过程中包含了领域知识。因此，我们的方法在同一时间跨度内执行1400个查询。他们也没有报告哪些是导致规避的最具影响力的突变：后者至关重要，我们正在处理统计算法中的潜在漏洞，与其他安全漏洞相比，这些漏洞的存在并不明显。

GAN[27]

Hu和Tan[17]开发了一个生成性对抗网络（GAN）[27]，其目的是绕过目标分类器，打造对抗性恶意软件。网络会了解哪些API导入应该添加到原始样本中，但不会生成真正的恶意软件，因为这种攻击只在功能空间内运行。相反，由于每次都会生成真实的样本，因此我们创建了功能正常的恶意软件。针对Windows恶意软件检测器的黑匣子攻击的概述见表V，其中我们将上述技术与我们的方法进行了比较。

六、CONCLUSION AND FUTURE WORK

在本文中，我们提出了一个基于学习的Windows恶意软件检测器的新的黑盒攻击家族，它既能有效地进行查询，又能保持功能，克服了以往工作的局限性。我们的攻击依赖于在恶意文件末尾或在新创建的部分中注入良性内容（这些内容永远不会被执行），利用用于在磁盘上存储程序的文件格式的模糊性，而不改变其执行痕迹。所提出的攻击被形式化为一个有约束的最小化问题，该问题能够在规避检测的概率和注入的有效负载大小之间进行优化。我们对两个流行的基于学习的Windows恶意软件检测器进行了广泛的实证评估，结果表明，即使目标模型只输出预测的标签，我们的黑盒攻击也可以通过很少的查询和非常小的有效负载绕过它们。我们还表明，我们的攻击可以成功地转移到其他商业防病毒解决方案，发现他们可以逃避，平均而言，多达12个商业防病毒引擎提供的VirusTotal。尽管如此，我们相信直接针对这些探测器的优化攻击可能会更加有效。未来工作：未来工作的一个有趣途径是调查针对我们的攻击的适当对策的适用性，如第节所讨论的。六、包括使用更健壮的特征表示（对基于字节或基于节的操作不敏感）和学习范式（通过对抗性再训练、特定攻击检测机制或使用领域知识约束）。另一个有希望的研究方向是将我们的攻击扩展到只在文件末尾或新创建的部分中注入内容的操作之外。我们坚信这是可以很容易实现的，因为我们的方法已经足够普遍，可以包含更广泛的功能保留操作，包括第节中讨论的操作。III-A级。将我们的工作扩展到处理也可以修改恶意软件程序动态执行的操作，例如在保留恶意意图的同时改变其控制流，无疑是一个挑战。然而，这无疑将为改进基于动态程序分析提取的特征的恶意软件检测器的评估和对抗性健壮性提供重要的一步。

AI安全（4）Black-Box Adversarial Attacks Against Deep Learning Based Malware Binaries Detection with GAN

发表于 2021-06-02 更新于 2023-05-06 分类于【draft】应用，学术前沿，网络安全， AI安全本文字数： 10k 阅读时长 ≈ 19 分钟

Black-Box Adversarial Attacks Against Deep Learning Based Malware Binaries Detection with GAN

摘要：

【目的】为了有效地检测恶意软件，有越来越多的基于原始软件二进制文件的深度学习方法。最近的研究表明，深度学习模型很容易被愚弄，通过对输入引入细微的扰动而做出错误的决定，这在对抗性攻击中吸引了大量的工作。【缺点】然而，大多数现有的攻击方法都是基于手动特性（例如API调用）或白盒设置，使得这些攻击在当前的现实场景中是不切实际的。【工作】在这项工作中，我们提出了一种新的攻击框架，称为GAPGAN，它通过生成对抗网络（GANs）生成对抗有效负载（填充字节）。据我们所知，这是第一个针对基于深度学习的恶意软件二进制文件检测在字节级别执行端到端黑盒攻击的工作。【创新一】在我们的攻击框架中，我们将输入的离散恶意软件二进制文件映射到连续空间，然后将其提供给GAPGAN的生成器以生成对抗性有效载荷。我们将有效载荷附加到原始二进制文件中，以便在保留其功能的同时创建一个对抗性示例。【创新二】我们建议使用动态阈值来减少有效载荷从连续格式映射回原始离散格式时的有效性损失。为了平衡生成器对有效负载和对抗性样本的关注，我们使用了一种自动权重调整策略。【结果】我们用恶意软件和良性软件训练GAPGAN。一旦训练完成，生成器可以在不到20毫秒的时间内生成一个只包含输入恶意软件的对抗性样本，我们应用GAPGAN攻击最先进的探测器MalConv，只需附加2.5%的有效负载即可达到100%的攻击成功率。我们也在不同的防御方法下攻击具有不同结构的深度学习模型。实验结果表明，GAPGAN在效率和有效性上都优于其他最新的攻击模型。

一、说明

深度神经网络已经取得了巨大的成功，越来越多的工作倾向于使用深度学习进行有效的恶意软件检测。其中，一些工作（例如，[5]和[12]）基于可能包含程序恶意行为的手动功能（例如，API调用）检测恶意软件，一些工作（例如，[21]、[24]和[4]）直接使用软件信息而不运行，其他工作（例如，[13]和[20]）集成上述策略或使用其他方法，如可视化。最近，有一种趋势是使用原始二进制文件进行恶意软件检测，它可以有效地挖掘文件不同部分之间的潜在关系。随着恶意软件的快速发展，防御效率在当今的现实场景中变得至关重要，这使得基于原始二进制文件的端到端检测更具前景。

然而，许多研究工作（[25]、[7]、[17]、[9]和[27]）表明，深层神经网络容易受到对抗性攻击。攻击者对原始数据添加了人类无法察觉的小干扰，这可能会误导分类器做出错误的决策。这些研究指出，深度学习算法和人工智能应用的安全性面临严重威胁。

在恶意软件检测中，大多数对抗性攻击（例如，[14]、[15]和[3]【问题空间扰动】）依赖于检测器的完整信息（例如，白盒攻击）。然而，这种攻击有其局限性，例如，目标模型必须完全暴露给攻击者。同时，之前的攻击工作（例如，[11]、[2]和[23] 【特征空间扰动】）基于推测用于训练探测器的手动特征。如果猜测是错误的，或者一旦后卫改变了训练策略，这种攻击将无效。基于原始二进制文件的检测的广泛使用也使得这种需要大量资源和时间来提取特征的攻击不适用。与手动特性不同，即使稍加修改，也不能简单地更改原始二进制数据，否则会损坏其功能。此外，二进制数据的大小差异很大，这进一步增加了攻击难度。我们还发现，在保存生成的对抗性样本时，将连续空间中的对抗性有效载荷转换回离散二进制时，会忽略细微的扰动，这会影响对抗性攻击的有效性。因此，如何在保护原有功能的同时，对基于恶意软件二进制文件的深度学习模型进行有效而实用的黑盒攻击仍然是一个巨大的挑战。本文提出了一种新的攻击框架GAPGAN，该框架通过GANs生成对抗性有效载荷。据我们所知，这是第一项针对基于深度学习的恶意软件二进制文件检测在字节级别执行端到端黑盒攻击的工作。我们应用GAPGAN攻击最先进的检测器MalConv[21]以及其他具有不同结构的深度学习模型。实验表明，我们的模型可以实现较高的攻击成功率，并且在效率和有效性方面优于其他最先进的攻击方法。

We have the following contributions:

我们提出了一种新的对抗性攻击框架GAPGAN，该框架在字节级对基于深度学习的恶意软件二进制检测执行端到端的黑盒攻击，使攻击更加高效。
在GAPGAN中，生成器生成对抗性有效载荷，ap将其挂起到原始数据，以制作恶意软件对抗性样本，同时保留其功能。一旦训练过程完成，生成器可以在不到二十毫秒的时间内高效地生成每个对抗性样本。
我们建议在将有效负载从连续空间映射回离散二进制文件时，使用动态阈值来减少有效负载有效性的损失。为了平衡生成器对有效负载和对抗性样本的关注，我们采用了自动权重调整策略。
我们应用GAPGAN攻击最先进的恶意软件检测器MalConv。实验表明，GAPGAN生成的对抗性样本在附加2.5%数据长度的对抗性有效载荷进行检测时，攻击成功率可达100%。实验还表明，GAPGAN在不同防御方式下的效率和有效性均优于其他最先进的攻击方法。

论文的剩余部分由五个部分组成：第二部分介绍了本文的研究背景和相关工作。在第3节中，我们将解释攻击框架GAPGAN的详细信息。在第4节中，我们描述了实验设置，包括数据集、指标和目标模型。在第5节中，我们展示了我们的实验结果。在第6节中，我们总结了我们的工作并给出了结论。

二、背景和相关工作

2.1 针对恶意软件检测的对抗性攻击

大多数用于恶意软件检测的传统机器学习和深度学习方法（例如，[5]和[12]）侧重于从程序的行为信息中提取的手动特征，如签名和API调用。对于这种检测方法，早期的攻击工作主要基于防守者应该使用的手动特征。一些工作建议使用API作为二进制特性，然后采用深度学习模型来生成对抗性样本（[11]和[8]）。一种基于API调用序列的不同方法使用优化过程来执行对抗性攻击【23】。[2] 建议使用强化学习进行攻击，它包含大量手动信息作为特征，例如PE头元数据、节元数据和字节直方图。Xu等人[29]提出了一种基于遗传编程的攻击方法，对文件结构进行随机操作。然而，这些攻击需要专家经验和大量的时间来获得有效的特征，一旦防御者知道用于攻击的特征，快速更新的检测器就可以轻松规避攻击。

最近的恶意软件检测工作（例如，[21]、[24]和[4]）更注重对原始软件二进制文件使用深度学习模型，因为深度神经网络可以有效地挖掘原始数据中的潜在特征，而无需大量数据预处理和先验经验。为了赶上最新的恶意软件检测技术，攻击者开始寻找可应用于原始软件二进制文件的新方法（例如，[14]、[15]和[3]）。与提取的特征不同，原始二进制数据不能简单地更改，否则可能会丢失重要功能。此外，原始二进制文件具有可变的输入大小，这会进一步使这些攻击比以前更加棘手。

[14] 提出了第一种字节级的对抗性攻击，它结合了梯度上升和贪婪策略。它会在文件末尾逐个追加字节，以保留其功能。然而，它执行的白盒攻击在现实场景中有局限性，模型需要计算每个填充字节的梯度，这会消耗大量时间和资源。[15] 还提出了一种通过注入局部扰动来处理离散序列的方法。但是，它处于白盒设置中，效率不高。[3] 提出了白盒和黑盒方法。在黑盒方法中，它随机选择良性数据块并将其附加到恶意软件数据中，每次都测试结果。在执行攻击之前，获取有效块需要大量时间。这种方法简单但繁琐且效率低下，不适用于有效的恶意软件对抗性样本生成。相反，我们将展示我们的端到端框架可以在黑盒环境中进行攻击，并在更短的时间内生成对抗性样本。

2.2 Generative Adversarial Networks (GANs)

近年来，生成性对抗网络（GANs）[6]广泛应用于计算机视觉任务中（例如，[30]、[16]和[1]）。根据他们的高水平模仿能力，一些作品（例如，[11]和[28]）采用GANs进行对抗性攻击。最具代表性的攻击方法使用称为蒸馏的方法将鉴别器与目标模型的输出相匹配，训练生成器生成可能误导鉴别器的数据。通过这种方式，敌对样本可以间接攻击目标模型，即敌对样本的可转移性[19]。与之前的工作不同，我们使用生成器生成对抗性有效载荷，用于在不破坏其功能的情况下制作对抗性样本。在我们的模型中，一旦GANs的训练过程完成，生成器可以在很短的时间内仅使用输入的恶意软件二进制文件独立生成恶意软件对抗样本。

三、方法

在本节中，我们将简要解释输入二进制文件和对抗性示例的形式化定义，然后介绍GAPGAN的框架和策略细节。

3.1 问题定义

【问题定义】软件的二进制文件由属于离散空间 $\mathcal{X}=\{0, \ldots, 255\}$ 的字节序列组成。设 $b=\left(b_1, \ldots, b_n\right) \in \mathcal{X}^n$ 表示一个二进制文件，其中$n$是字节序列的长度，因文件而异。二进制文件$b$带有标签$y \in\{-1,1\}$，其中$y=1$表示它是良性软件$b_{b e n}$，否则它是恶意软件$b_{m a l}$。

恶意软件检测器旨在学习一个映射函数$f$ : $x \rightarrow\{-1,1\}$，满足$f\left(b_{\text {mal }}\right)=-1$和$f\left(x_{\text {ben }}\right)=1$。相反，对抗攻击的目标是找到一个模型$g$并生成一个有效的对抗样本 $b_{a d v}=g\left(b_{m a l}\right)$ ，使得恶意软件检测器将其分类为良性软件，即$f\left(b_{a d v}\right)=1$。同时，$b_{a d v}$必须保留$b_{\mathrm{mal}}$的原始功能。【可执行】

3.2 GAPGAN：

【框架流程概述】图1显示了拟议框架GAPGAN的概述。它包括两个阶段：训练过程和进攻过程。在训练过程中，我们同时训练生成器网络G和鉴别器D，其中G打算为输入恶意软件生成对抗性有效载荷，并将它们连接起来以制作对抗性样本，而D试图提取目标黑箱检测器f，并模仿f对原始良性样本和生成的对抗性样本的判定。在攻击过程中，我们只需要经过训练的生成器来攻击黑箱检测器。

【扰动添加概述】为了在制作恶意软件的对抗性示例时保护其原始功能，有一些流行的方法，如使用调试日志和在运行前压缩数据，但它们是费时费力。通过仔细选择和操纵执行的其他攻击非常复杂，可能需要特定的经验，不适用于有效的对抗性攻击。受之前工作（[3]和[14]）的启发，我们选择在文件末尾附加字节（有效载荷）以保留其功能，这很简单，不需要任何专家经验.

【数据预处理】由于软件文件的长度$n$变化很大，我们首先将零（表示为图1中的蓝色部分）附加到输入二进制文件的末尾，以匹配网络的输入大小$t$，即$b^{\prime}=\left(b_1, \ldots, b_n, 0, \ldots, 0\right) \in \mathcal{X}^t$，其中$t \geq n$。通过这种方式，我们可以将不同长度的每个样本输入到具有固定大小的特定网络中。然后，我们通过归一化将离散二进制中的每个字节映射到连续空间$[-1,1]$。我们将归一化后的输入定义为$x$，其中$x=\left(x_1, \ldots, x_t\right) \in \mathbb{R}^t$。【值得注意的是，为了保留可执行文件的多态性，没有将输入进行归一化。】

在数据预处理之后，将标准化的恶意软件xmal馈送到生成器G。然后，G基于xmal的相应特征生成对抗性负载aadv(在图1中表示为红色部分)：

\[ aadv = G(xmal) (1) \]

我们将aadv附加到xmal的末尾以制作对抗性恶意软件样本xadv;

\[ xadv = [xmal，aadv] \]

其中[·，·]表示连接操作。

在训练D时，我们将xadv和xben都合并到数据池中。在每次迭代中，我们从数据池中抽取混合示例批次，然后使用它们来查询黑盒检测器f。接下来，我们使用f响应的标签来拟合D，使得D的决策边界尽可能接近f。

在训练过程中，生成器G学习创建可以避开鉴别器D的样本。此外，随着D和我们的目标模型f之间的相似性的提高，G对f的对抗性攻击能力也将提高。最后，由于对抗性攻击的可转移性，G生成的对抗性样本也可以有效地避开f。

一旦训练过程完成，我们就可以使用训练后的G在很短的时间内生成对抗性样本，只需输入恶意软件。值得注意的是，我们在攻击过程中放弃了填充零，以减少有效载荷的整个长度。根据我们的实际经验，这会使攻击成功率略有下降，但损失是可以接受的。此外，我们需要将对抗性样本转换回离散空间作为可执行文件。

【模型结构】为了使我们的框架适应不同长度的恶意软件二进制文件和有效负载，生成器网络设计为具有可变的输入和输出大小。更具体地说，生成器首先使用两个卷积层提取输入的特征。然后，它使用完全连接的图层调整高级特征的大小。经过两层反卷积和一层1∗ 1卷积，产生对抗性有效载荷。另一方面，鉴别器使用卷积层和完全连接层进行二元分类。请注意，如果确定了输入数据的大小和我们决定生成的有效负载的长度，我们可以使用它们作为输入来轻松调整GAPGAN的结构，因为生成器和鉴别器中的层都是完全连接的。

3.3 Black-box Attacks Strategy

生成器G：

将n长度的字节序列添加到t长度（t>n)

通过标准化将离散二进制文件中的每个字节映射到一个连续空间[-1,1]

将填充后的恶意软件样本输入到生成器生成对抗样本$adv$

讲对抗样本$adv$添加到填充后的恶意软件样本后

检测器D:

将对抗样本和良性样本中抽取在黑盒上打标签

用黑盒打上的标签数据去拟合检测器D，使得D的决策边界尽可能接近黑盒

训练结束：

在攻击过程中放弃了填充零，以减少有效负载的整个长度。

将对抗性样本转换回离散空间作为可执行文件

生成器：生成器G的目的是学习Xmal的特征，Xmal的原始标签是y=−1，并生成相应的有效样本Xadv，这会误导D将其预测为y=1的“良性”。在我们的实践经验中，G往往更关注D对xadv的预测结果，这带来了一个严重的问题，即对抗有效载荷aadv的有效性得不到很好的提高。因此，我们让G同时考虑xadv的全局和局部（即xadv和aadv）有效性。生成器G的对抗性损失函数为： \[ LG = −(1 − β)Ex∼pxadv(D(x)) − βEa∼paadv(D(a)) \]

其中，β是一个超参数，用于在xadv和aadv之间保持生成器注意力的平衡。我们试图找到β的最佳值，然而，固定的β并不总是表现得最好，因为每次攻击程序运行时，网络的条件都不同。因此，最好的β应该具有自适应调整的能力。受[18]的启发，我们考虑根据D到xadv和aadv的输出自动调整β，这分别代表了它们的攻击有效性。我们给出了自动调谐机制：

如果xadv比aadv更有效，那么D到xadv的输出期望就更大。自动机构将增加β 间接提高aadv的学习率。我们将在实验中证明它的有效性。

【介绍动态蒸馏】

判别器：我们使用鉴别器D来动态提取目标黑盒模型f。更具体地说，我们从数据池中采样一批混合数据，通过查询f来获得标签。样本及其相应的标签用于基于距离度量H拟合D。D的蒸馏损失为：

D试图学习f对xben和xadv的决策策略。通过这种方式，D被视为替代检测器，用于将对抗性样本的攻击有效性转移到最终目标黑盒模型f。

动态阈值策略：在攻击过程中，我们将生成敌方样本并保存在本地。然而，我们发现当我们将对抗性样本从对抗性连续空间映射回二进制的离散空间时，细微的扰动将被忽略。大部分包含攻击有效性的有效载荷将被忽略，因为它们的值很小。为了解决这个问题，我们建议使用动态阈值策略来限制有效载荷的最小值：

其中e表示有效载荷中的每个字节，i是当前训练迭代时间，Tmax是最大训练迭代时间，西格玛是最大阈值。我们直接将具有小值的字节设置为阈值以下的零。然而，如果我们使用静态阈值，G的学习过程将会丢失。如果一个字节的值很小，但有一定的攻击效果，它首先会被设置为零的阈值。然后G将继续对字节或其他相邻字节添加扰动，以提高该区域的对抗攻击效能。最后该字节或其他相邻字节将被修改，以填充设置为零的字节的对抗攻击损失。

值得注意的是，在我们设置后，所有的调整过程都将使用梯度下降算法自动执行 . 在上述工作的基础上，黑匣子攻击对恶意软件检测的总体算法如算法1所示。在第5节中，我们将展示我们的攻击实验的细节。

四、实验装置（EXPERIMENTAL SETUP）

本节介绍了我们的攻击实验准备工作，包括数据集、评估指标以及我们选择和训练的目标模型。

4.1 数据集

研究二进制文件长度对攻击的影响

恶意软件和良性软件数据从不同来源收集，用于我们的对抗性攻击实验，如表1所示。恶意软件样本从VirusTotal4和Microsoft恶意软件分类挑战赛（Kaggle 2015）下载【22】。良性软件示例由Windows软件包管理器Chocolate Software5下载。将数据分为四个数据集，使恶意软件的二进制长度分布接近每个数据集中的良性软件。使用具有不同最大和平均长度的数据集1、2和3来研究二进制文件长度对攻击的影响。数据集2和数据集4具有不同的来源，但长度分布很近，用于评估攻击算法的泛化。

评估方法：攻击成功率（ASR）指标

4.2 Target Black-box Models

四种目标模型

我们选择最先进的恶意软件检测器MalConv[21]作为我们的主要目标黑箱模型。MalConv首先将输入二进制文件中的每个字节嵌入到8维向量中，然后使用两个具有不同激活函数的卷积层进行分类。我们为每个数据集训练一个输入大小为2000000的MalConv检测器。表2显示了每个MalConv探测器在培训后的测试精度。它表明，经过训练的MalConv检测器具有与[21]中类似的性能。

为了测试对抗攻击方法的泛化性，我们还使用了四种不同结构的深度学习模型作为目标模型。为了减少输入二进制文件的大尺寸，我们考虑在每个深度学习模型中添加CNN结构。输入二进制文件中的每个字节都以与MalConv相同的方式嵌入到8维向量中。我们在数据集2和4上训练这四个模型，检测精度如表2所示。结果表明，这四种检测器也达到了较好的分类精度。

五、EXPERIMENTAL RESULTS

在本节中，我们将展示GAPGAN在对抗性攻击实验中的有效性。我们还将其与不同防御下的其他最先进的攻击方法进行了比较。

我们首先应用GAPGAN以不同长度的对抗性有效载荷攻击四个经过训练的MalConv（我们在上一节中展示了它们）。有效负载率用于表示有效负载长度与二进制文件长度的比率，以进行检测。根据表3所示的对不同数据集的攻击性能，可以看出GAPGAN可以对MalConv模型执行有效的黑盒攻击。从数据集2和数据集4的结果可以看出，敌对样本对不同数据的攻击成功率较高。此外，由于有效载荷率的增加，原始长度较短的对抗性二进制文件可能具有更好的攻击效果。值得一提的是，从数据集1生成的对抗性样本的ASR可以达到100%，只有一小部分有效载荷，即检测数据总长度的2.5%。

我们发现，当ASR已经达到很高的值时，使用较大的有效负载可能只会提高很少的攻击成功率（例如，当附加10%的有效负载时，ASR为98.21%，但当附加两倍长度的有效负载时，ASR仅提高1.79%）。然而，随着有效载荷长度的增加，被检测的风险和成本将增加。同时，为了证明GAPGAN生成的对抗性有效载荷的有效性，我们将其与随机有效载荷进行比较，如图2所示。我们发现，与随机生成的有效载荷相比，具有GAPGAN生成的有效载荷的对抗性样本具有更好的攻击效果。还可以看出，随机有效载荷的ASR与有效载荷率成正比，而对抗性有效载荷随着有效载荷率的增加而迅速增加，当达到较高值时，ASR的增长速度减慢。我们认为，每个数据集都存在最佳的有效负载率，即当附加较大的有效负载时，ASR的增长率将快速下降。

5.2 与最新攻击方法的比较

黑盒、速度、攻击等级

基于梯度优化的方法：Adversarial malware binaries: Evading deep learning for malware detection in executables

基于API调用序列的AdvSeq方法：Generic black-box end-to-end attack against state of the art API call based malware classifiers

基于API调用序列的MalGAN

我们将GAPGAN与恶意软件检测任务中其他最先进的对抗性攻击方法进行了比较，即Opt。基于梯度优化的方法【14】、基于API调用序列的AdvSeq方法【23】和基于API调用和GANs的MalGAN方法【11】。其结果如表4所示。可以看出，只有Opt。方法在白盒设置中执行攻击。从攻击效率的角度来看，一旦攻击模型得到训练，GAPGAN和MalGAN生成对抗性样本的速度远远快于其他方法（AdvSeq也基于复杂的优化过程，这被认为是无效的）。然而，只有GAPGAN在字节级别执行有效的黑盒攻击，这在现实场景中更具威胁性。为了进一步探索针对基于二进制文件的检测的攻击方法的有效性，我们选择比较GAPGAN和Opt。方法，即字节级攻击方法。选择具有随机有效载荷的对抗性样本进行比较。从表5可以看出，这两种攻击方法对不同的检测器都具有良好的攻击性能。然而，GAPGAN执行高效的黑盒攻击，这被认为是应用程序中对抗性攻击的关键。

针对二进制文件检测的攻击方法的有效性，我们选择GAPGAN和Opt进行比较，两种攻击方法对不同的检测器都有很好的攻击性能。然而，GAPGAN执行高效的黑盒攻击，这对于应用中的对抗性攻击至关重要。

5.3 不同防御方式下的攻击性能

人们提出了许多防御方法来防御各种攻击。使模型对对抗性样本具有鲁棒性的最常用方法是对抗性训练[7]，它在训练过程中引入对抗性扰动，使深度学习模型调整决策策略。另一种有效的防御方法[26]随机消除输入数据，以消除对抗性样本的攻击有效性。我们比较了随机有效载荷与GAPGAN和Opt生成的对抗性样本的攻击效果。在这些防御之下。为了模拟真实场景，我们假设攻击者不知道有关防御的任何信息。在RND防御方法的实验中，我们随机消除10%的输入数据，并测试对抗样本的攻击成功率。由于检测器的结构包含一个嵌入层，因此在对抗性训练防御方法中无法传递梯度。因此，我们建议使用用于提取检测器的替代模型来生成具有对抗性干扰的训练数据。新的训练数据用于提高检测器的鲁棒性。使用之前的探测器生成的对抗性样本将在重新培训的探测器上进行评估。表6显示了防御攻击的结果。我们表明，在大多数情况下，GAPGAN的攻击性能优于Opt。方法，尤其是在对抗性训练的防守下。一种可能的解释是Opt。该方法过度依赖于目标模型的结构和梯度信息。此外，有效载荷中的一个字节由Opt根据当前敌对样本的梯度生成。方法在RND防御的随机置零过程中，当字节之间的连接被切断时，攻击的有效性会受到很大的损害。相比之下，GAPGAN考虑了整个对手样本的攻击能力，使其在防御下更有效。

为了防御各种攻击，人们提出了许多防御方法。使模型对对抗性样本具有鲁棒性的最常用方法是对抗性训练Explaining and harnessing adversarial examples，它在训练过程中引入对抗性扰动，使深度学习模型调整决策策略。另一种有效的防御方法随机消除输入数据 Adversary resistant deep neural networks with an application to malware detection，以消除对手样本的攻击效果。我们比较了随机有效载荷与GAPGAN和Opt生成的对抗样本的攻击效果。在这些防御之下。

在大多数情况下，GAPGAN的攻击性能优于Opt。方法，尤指在对抗性训练的防守下。

5.4 动态参数的使用效果

集成比列调节

W: without using the method; S: using static parameter; D: using dynamic parameter

动态阈值和自动权重调整策略显著提高了对抗性样本的有效性

六、结论

在本文中，我们基于GAN的思想提出了一个对抗性攻击框架GAPGAN来生成对抗性样本，以对抗基于二进制文件的恶意软件检测。在我们的模型中，我们将生成器生成的对抗性有效负载附加到原始恶意软件二进制文件中，以在不破坏其原始功能的情况下创建一个对抗性示例。实验表明，GAPGAN可以有效地攻击最先进的检测器MalConv以及其他不同结构的深度学习模型。结果还表明，在现有防御机制下，我们的模型在效率和有效性上都优于其他最先进的攻击方法。GAPGAN是第一个实用的针对恶意软件检测的端到端黑盒攻击框架，对下一代流行的检测技术，即基于原始二进制文件的恶意软件检测构成威胁。虽然我们的工作集中在恶意软件二进制文件，它可以很容易地扩展到其他领域，如对抗性文本或图形生成。这使得GAPGAN成为一个很有前途的攻击框架，用于提高恶意软件检测或其他任务防御方法的健壮性。

恶意软件检测（13）Dynamic Malware Analysis

发表于 2021-05-29 更新于 2023-04-19 分类于【draft】应用，学术前沿，网络安全，恶意软件检测本文字数： 4.1k 阅读时长 ≈ 7 分钟

Dynamic Malware Analysis in the Modern Era—A State of the Art Survey

本次调查的目的是对用于动态分析恶意软件的现有方法进行全面和最新的概述，其中包括对每种方法的描述、其优缺点以及对恶意软件规避技术的适应性。此外，我们还概述了利用机器学习方法来增强动态恶意软件分析能力的一些重要研究，这些研究旨在检测、分类和分类。

学习内容：

分析方法：易失性内存取证（volatile memory forensics）、侧通道分析（side-channel analysis）

动态分析的意义：

虽然恶意软件编写者可以使用各种技术（如代码混淆、动态代码加载、加密和打包）来逃避静态分析（包括基于签名的防病毒工具）态分析对这些技术是健壮的，并且可以提供关于所分析文件的更多理解，因此可以导致更好的检测能力。

动态分析的局限性：

只有执行的代码是可观察的。这意味着，如果没有精确地满足所需的条件，那么某些代码可能无法执行，从而无法进行分析。Deeplocker
动态分析还需要计算开销，这可能会降低执行速度。
分析必须在恶意软件针对的特定操作系统和/或硬件上执行。

说明：

物联网设备是另一个可以受益于内存分析的平台示例，因为基于软件的新检测机制的设计和安装并不简单。此外，由于物联网设备具有有限的计算资源，现有的动态分析技术对于此类设备可能不太相关或有效。

恶意软件分类

Classification of Malware by Type
Classification of Malware by Malicious Behavior
Classification of Malware by Privilege
About Behavior and Privilege

ANALYZING MALWARE BEHAVIOR

动态恶意软件分析框架描述

分析技术和学术工具

函数功能分析
- 每个进程都依赖函数调用来执行其职责，不管这些函数是进程内部的还是外部的（例如，由其他进程导出的函数、系统调用）。通过跟踪恶意软件调用的各种函数以及与这些函数相关的参数，可以更好地了解所分析恶意软件的行为。调用函数时获取通知可以通过将一段代码Hooking到该函数来实现。
  - hooking mechanism
  - code injection
- TTAnalyze(LastLine)是一个分析工具，它用一个称为Inside the Matrix（insideetm）的客户机组件扩展了QEMU仿真器，该组件将虚拟地址转换为物理地址。
- CWSandbox基于将可信DLL的代码注入到分析的进程中，该进程通过覆盖导出地址表（EAT）中的条目并将执行重定向到CWSandbox来拦截函数调用。CWSandbox收集大量的信息（比如被调用函数的名称、参数、系统状态等），然后将这些信息呈现给用户。
- Capture使用三个监视器分析操作系统的状态：文件系统监视器（跟踪所有硬盘上的读/写事件）、注册表监视器（跟踪多个注册表事件，如OpenKey、CreateKey等）和进程监视器（跟踪进程的创建和终止）。所有监视器都提供其他数据，如触发事件的进程、完整路径和时间戳。使用内核驱动程序，捕获与上述每个监视器对应的内核事件。最终结果是恶意软件触发的事件列表，以及它们的时间戳和参数。
- MalTRAK是一个跟踪恶意软件行为并扭转其影响的框架。它使用内核模式组件并将自身与关键函数挂钩，以跟踪恶意软件的操作，同时提供撤消这些操作的机制。
- dAnubis是用来分析内核驱动程序和检测rootkit的。它使用一个in-guest组件来监视rootkit和系统其余部分之间的通信。触发器引擎调用各种windowsapi调用来显示rootkit（定义为一组在恶意软件中获得root访问权限、完全控制目标操作系统和其底层硬件的技术编码）的存在（例如，隐藏的进程或文件）。
Execution Control 执行控制

动态恶意软件分析应该包含一种机制，偶尔停止恶意软件的执行，并检查恶意进程和操作系统的状态。执行控制技术包括：
- Debugging调试（也称为单步）是一种可靠的分析技术，最初是为了帮助程序员发现代码中的错误而开发的。使用CPU的陷阱标志在每个操作码指令后生成中断，调试器可以允许恶意软件在强制上下文切换回分析进程之前只运行一条操作码指令，然后分析进程可以检查恶意软件和操作系统的状态。
- 等
Flow Tracking 流量跟踪

细粒度分析用于跟踪通过恶意软件执行代码的信息流（例如，当一个函数的结果用作调用另一个函数的参数时）。
- Data Tainting
- Vigilite是一种分析工具，它使用二进制工具实现数据污染。最初是为了检测和阻止蠕虫的传播而开发的，Vigilite寻找来自网络的受污染数据的执行。因此，污点源是网络，当指令指针（IP）指向污点数据时，污点接收器就到达了，这意味着一些来自网络的不可信代码正在被执行。
- Panorama最初是一个TEMU插件，用于对各种I/O设备（包括硬盘、键盘或鼠标）进行污染分析。后来成为一个独立的平台。全景图的输出是以图形的形式提供的，它允许用户跟踪进程和内存区域之间的数据流。
- Dytan是Pin仪器系统的一个扩展，为数据污染提供了一个易于使用的API。它的开发采用了灵活的设计，允许用户配置各种组件，如污染源、污染汇、数据流跟踪器和控制流跟踪器。Dytan可以配置为跟踪显式和隐式信息流。此外，它的功能可以通过使用回调函数来扩展，回调函数实现额外的污染源、标签、传播和接收器。
- TQana是一个构建在QEMU之上的框架，用于分析和检测安装在internetexplorer上的恶意浏览器扩展。它使用带有两个污点源的数据污点：（1）用户访问的页面的所有URL字符串和（2）浏览器收到的响应其请求的信息。污点接收器是文件系统、注册表和网络。当受污染的数据被写入文件或通过网络发送时，被分析的样本就被怀疑是间谍软件。
Tracing 追踪

收集执行某些代码后留下的信息称为跟踪。网络连接和分配给恶意软件的内存会留下恶意软件行为的痕迹。分析这些痕迹可以提供有关恶意软件的见解，而无需使用客户端组件中的。
- Volatile memory analysis 易失性内存分析分析从内存转储文件分析恶意软件的影响（见第6.5节）需要了解操作系统如何跟踪进程、文件、用户和配置。所有这些数据结构都以二进制形式存在于内存转储中。
- Network Tracing 网络跟踪由于恶意软件在大多数情况下需要连接Internet才能执行其操作，因此在没有Internet访问的情况下，可能无法显示恶意软件的确切性质。然而，允许恶意软件完全访问互联网有时是不可取或不可能的。通过恶意软件限制网络访问并分析网络连接可以揭示恶意软件的C&C和从中收到的命令。恶意软件留下的网络痕迹有助于理解其呈现的通信模式。
- HookFinder是TEMU实现的另一部分，旨在通过分析易失性内存来检测和分析恶意钩子。在堆栈中找到的信息被转换为创建钩子图，这有助于识别钩子链。然后，HookFinder将属于恶意软件的内存段标记为污点接收器。为了验证钩子实际上是由恶意软件安装的，HookFinder调用各种函数调用，并通过检查指令指针（IP）来跟踪控制流。当IP指向受污染的内存时，恶意钩子就会被发现并验证。
- LiveDM利用QEMU来分析内核中新内存区域的分配。通过挂接操作系统实现的几个内存分配函数，它可以跟踪恶意软件的安装位置，并对恶意软件的二进制代码执行静态分析。使用模拟器对客户操作系统的控制，LiveDM能够获得客户操作系统的易失性内存并分析受感染的内核。
- 等
Side-channel Analysis
- 到目前为止提出的分析技术依赖于从操作系统、易失性存储器或仿真机器的状态中提取数据。然而，任何类型的计算设备都可能成为恶意软件的攻击目标。这些设备包括PCI卡、物联网设备、硬盘、医疗设备等。分析和检测这些设备上运行的恶意软件是困难的，因为大多数情况下，这些设备不包含一个操作系统，可以支持传统的分析技术。与从操作系统的角度（或二进制级别）跟踪系统的行为不同，可以通过物理组件的功耗、电磁辐射或内部CPU事件来分析它们的行为。获取的数据分为“正常行为”和“感染行为”。使用统计方法和机器学习算法，检测到偏离正常行为可能表明CPU行为异常（例如，存在cryptominer或rootkit）。侧通道分析无法提供有关操作系统、网络或正在修改的文件的内部事件的深入信息。没有向仅仅收到最终判决的用户提供报告（称为恶意或非恶意）。
- WattsUpDoc是一种分析工具，用于使用外部设备对医疗设备进行侧信道分析。它证明了侧通道分析可以用于分析没有操作系统的设备，而无需向分析的设备加载任何代码。

布局映射技术（MAPPING TECHNIQUES TO LAYOUTS）

恶意软件和分析工具之间的战争是一场军备竞赛。攻击者不断开发新的方法来规避和检测分析框架，同时负责检测恶意软件的分析框架和工具的能力也在不断提高。创建图13是为了帮助读者理解这场军备竞赛以及攻击者和分析人员使用的不同方法。

综合比较研究

本部分比较了近年来动态恶意软件分析的研究，并讨论了与此相关的趋势和参数。进行此比较，我们可以发现一些重要的见解，我们也与读者分享。

基于功能和实际方面的比较
- 我们的比较基于以下几个关键方面：
  
  （1）该工具的相关性（其对科学界的影响和贡献基于引文数量和是否开源），
  
  （2）该工具提供的分析的多功能性，
  
  （3）用于实现该工具的分析布局（见第6节），
  
  （4）工具的限制（预分析要求、所依赖的附加软件、特殊要求的硬件）和
  
  （5）工具提供的输出。请注意，这些工具是按分析技术分组的，在每种技术中，它们是按出版年份排序的。关于图14的详细说明如下：

算法长征-代码随想录

发表于 2021-05-07 更新于 2022-05-19 分类于【draft】工程，数据结构本文字数： 12k 阅读时长 ≈ 22 分钟

一、树状数组

leecode 题目：数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4] 输出: 5

「树状数组」是一种可以动态维护序列前缀和的数据结构，它的功能是：

单点更新update(i, v):把序列 $i$ 位置的数加上一个值$v$，这题 v = 1
区间查询 query(i)： 查询序列[1⋯i] 区间的区间和，即 i 位置的前缀和

修改和查询的时间代价都是 $O(\log n)$，其中 n 为需要维护前缀和的序列的长度。

二、单调栈

通常是一维数组，要==寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置==，此时我们就要想到可以用单调栈了。

单调栈里存放的元素是什么？

单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。
单调栈里元素是递增呢？还是递减呢？

注意一下顺序为从栈头到栈底的顺序，因为单纯的说从左到右或者从前到后，不说栈头朝哪个方向的话，大家一定会越看越懵。
目标列表遍历顺序？ 倒序？正序？

2.1 下一个更大元素

def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
    # 下一个更大的元素：单调栈(不增的不要) + 哈希 
    res = {}
    stack = []
    for num in reversed(nums2): # 倒序？
        while stack and num >= stack[-1]:
            stack.pop()
        res[num] = stack[-1] if stack else -1
        stack.append(num)
    return [res[num] for num in nums1]

2.1 下一个更大元素2（循环数组）又TM是循环

    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 三次逆转
        s = list(nums[::-1])
        res = []
        for num in nums[::-1]:
            while s and s[-1] <= num:
                s.pop()
            if s:
                res.append(s[-1])
            else:
                res.append(-1)
            s.append(num)
        res.reverse()
        return res
"""
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 2n 遍历
        n = len(nums)
        ret = [-1] * n
        stk = list()
        for i in range(n * 2 - 1):
            while stk and nums[stk[-1]] < nums[i % n]:
                ret[stk.pop()] = nums[i % n]
            stk.append(i % n)
        return ret
"""
"""
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        # 栈留判断
        n = len(nums)
        ans = [-1 for _ in range(n)]
        stack = [0]
        stack2 = []
        for i in range(1, n):
            while stack and nums[i] > nums[stack[-1]]: # ？
                ans[stack[-1]] = nums[i]
                stack.pop() 
            stack.append(i)
        while len(stack) > 1: # 栈顶是最大的保留
            for num in nums: # 从头找？
                if num > nums[stack[-1]]:
                    ans[stack[-1]] = num
                    break
            stack.pop()
        return ans
"""

2.3 每日温度

def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
    # next Geater 
    n = len(temperatures)
    res = [0 for _ in range(n)] 
    stack = [0] # 存的初始索引
    for i in range(1, n): # 正序
        while stack and temperatures[i] > temperatures[stack[-1]]:
            res[stack[-1]] = i - stack[-1]  # stack[-1]
            stack.pop() 
        stack.append(i)
    return res

2.4 接雨水

接雨水是找每个柱子左右两边第一个大于该柱子高度的柱子。

def trap(self, height: List[int]) -> int:
    # 单调栈 左 弹出后 s.top() 中 s.pop()  右 height[i]
    n = len(height)
    stack = [0]
    res = 0
    for i in range(n):
        while stack and height[i] > height[stack[-1]]:
            mid = stack.pop() # 弹一个左面还有的话就是有坑
            if stack:
                high = min(height[stack[-1]], height[i]) - height[mid] 
                # 高 = 左右最小 - 低
                weith = i - stack[-1] - 1 # 宽
                res += weith * high 
        stack.append(i)
    return res

2.5 柱状图的最大矩形

找每个柱子左右两边第一个小于该柱子的柱子。：==栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度==

def largestRectangleArea(self, heights: List[int]) -> int:
    # 单调栈 左右两边都可以用
    heights.insert(0, 0)
    heights.append(0)
    stack = [0]
    ans = heights[0]
    for i in range(1, len(heights)):
        while stack and heights[i] < heights[stack[-1]]:
            mid = stack.pop()
            if stack: # 存在左右最小
                weith = i - stack[-1] - 1
                # high = max(heights[i], heights[stack[-1]])
                ans = max(ans, heights[mid] * weith)
        stack.append(i)
    return ans

三、单调队列

贪心算法大纲

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

贪心一般解题步骤

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

首先，动态规划问题的一般形式就是==求最值==。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。求解动态规划的核心问题是穷举。首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「==备忘录」或者「DP table」==来优化穷举过程，避免不必要的计算。而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的「状态转移方程」，才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我研究出来的一个思维框架，辅助你思考状态转移方程：

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

5.1 背包问题

https://leetcode-cn.com/problems/coin-change/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-wan-q-80r7/

1、确定dp数组以及下标的含义

2、确定递推公式

3、dp数组如何初始化

最大长度

递推等号左侧要初始化

4、确定遍历顺序

滚动数组

5、举例推导dp数组

5.1.1 背包递推公式

问==能否装满背包==（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

==问装满背包有几种方法==：dp[j] += dp[j - nums[i]] ，对应题目如下：

动态规划：494.目标和(opens new window)
动态规划：518. 零钱兑换 II(opens new window)
动态规划：377.组合总和Ⅳ(opens new window)

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。
动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满==最大价值==：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

动态规划：474.一和零

问装满背包所有物品的==最小个数==：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

5.1.2 遍历顺序

01背包

在动态规划：关于01背包问题，你该了解这些！ (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

和动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的，大家需要注意！

完全背包

说完01背包，再看看完全背包。

在动态规划：关于完全背包，你该了解这些！ (opens new window)中，讲解了纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求==组合数==就是外层for循环遍历物品，内层for遍历背包。

如果==求排列数==就是外层for遍历背包，内层for循环遍历物品。

5.2 子序列问题

动态规划：最长递增子序列

# 子序列 
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        dp = [1] * len(nums)
        result = 0
        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
            result = max(result, dp[i]) #取长的子序列
        return result

def lenLongestFibSubseq(self, A: List[int]) -> int:
    # 基本顺序是 k，i，j 或者 A[k] = A[j] - A[i]
    n = len(A)
    dic = {}
    # 创建索引字典，提速
    for ind,val in enumerate(A):
        dic[val] = ind
    # 初始化，行代表的是i，不需要取到n-1，为了给j留出位置
    # 初始为2，只要包含了 j i 位置，则意味着已经有了2个数字。
    dp = [[2]*n for _ in range(n-1)]
    ret = 0
    # 因此i只能取到n-2，给j留出空间
    for i in range(1,n-1):
        # j从i+1开始，毕竟j在i后面
        for j in range(i+1,n):
            diff = A[j] - A[i]
            if diff in dic and dic[diff] < i:
                k = dic[diff]
                dp[i][j] = dp[k][i] + 1 # 这个1，代表着k位置数字
                ret = max(ret,dp[i][j])
    return ret

动态规划：最长重复子数组

class Solution:
    def findLength(self, A: List[int], B: List[int]) -> int:
        dp = [0] * (len(B) + 1)
        result = 0
        for i in range(1, len(A)+1):
            for j in range(len(B), 0, -1):
                if A[i-1] == B[j-1]:
                    dp[j] = dp[j-1] + 1
                else:
                    dp[j] = 0 #注意这里不相等的时候要有赋0的操作
                result = max(result, dp[j])
        return result

动态规划：最长公共子序列、动态规划：不相交的线

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 最长子序列 
        m, n = len(text1), len(text2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                if text2[j-1] == text1[i-1]:
                    dp[i][j] = dp[i-1][j-1] +1 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

动态规划：最大子序和【贪心】【动态规划】

def maxSubArray(self, nums: List[int]) -> int:
    # 为什么dp[-1]不是最大？需要res
    # dp[i] 以i结尾的最大子数组和
    n = len(nums)
    if n == 0:
        return 0
    dp = [0] * (n)
    dp[0] = nums[0]
    for i in range(1, n):
        dp[i] = max(dp[i-1]+nums[i], nums[i])
    return max(dp)

动态规划：判断子序列【双指针】

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        n, m = len(s), len(t)
        i = j = 0
        while i < n and j < m:
            if s[i] == t[j]:
                i += 1
            j += 1
        return i == n

# dp[i][j] : word1[i-1], word1[j-1] 最少步数
# word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况 *  min(dp[i-1][j], dp[i][j-1])+1  
  def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(n+1):
            dp[0][i] = i
        for j in range(m+1):
            dp[j][0] = j
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1])+1 # , dp[i-1][j-1]+1
        return dp[-1][-1]

# 中心扩展法
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 枚举+中心扩展法
        def extendCenter(left, right):
            while 0 <= left and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            # 返回的为while不成立的值
            return left+1, right-1 
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = extendCenter(i,i)
            left2, right2 = extendCenter(i,i+1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start:end+1]

def longestPalindrome(self, s: str) -> str:
    # dp[i][j]: 是否是回文 dp[i+1][j-1] -> dp[i][j]
    # 返回的子串，不是数字 不能记录长度
    n = len(s)
    dp = [[False] * n for _ in range(n)] # 右上为1
    for i in range(n):
        dp[i][i] = True
    begin = 0
    maxlen = 0
    # 判断是否是回文子串中，如果是则记录begin and len
    for i in range(n-1, -1,-1):
        for j in range(i,n):
            if s[i] == s[j]:
                if j - i <=1:
                    dp[i][j] = True
                elif dp[i+1][j-1]:
                    dp[i][j] = True
            
            if dp[i][j] and j - i + 1 > maxlen:
                maxlen = j - i + 1
                begin = i

    return s[begin:begin+maxlen]

Manacher 算法

Manacher 算法是在线性时间内求解最长回文子串的算法。在本题中，我们要求解回文串的个数，为什么也能使用 Manacher 算法呢？这里我们就需要理解一下 Manacher 的基本原理。

奇偶长度处理： abaaabaa 会被处理成 #a#b#a#a##a#b#a#a#
==$f(i)$ 来表示以 s 的第 i 位为回文中心，可以拓展出的最大回文半径（包括 # ）==，那么$ f(i) - 1$就是以 i 为中心的最大回文串长度。
利用已经计算出来的状态来更新 f(i）：回文右端点rm ：i + f(i) - 1

动态规划：最长回文子序列

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 最大回文长度
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 and j - i >=2
        n = len(s)
        dp = [[0] * i +[1] * (n-i) for i in range(n)] # 从定义出发 右上三角 = 1 有意义
        for i in range(n-1,-1,-1):
            for j in range(i+1,n): # j - i >=2
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2 
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])                
        return dp[0][n-1]

class Solution:
    def minCut(self, s: str) -> int:
        # 动态规划1:判断回文
        n = len(s)
        g = [[True] * n for _ in range(n)]

        for i in range(n - 1, -1, -1):
            for j in range(i + 1, n):
                g[i][j] = (s[i] == s[j]) and g[i + 1][j - 1]
        # 
        f = [float("inf")] * n
        for i in range(n):

            if g[0][i]:
                f[i] = 0
            else:
                for j in range(i):
                    if g[j + 1][i]:
                        # （0, j) + (j+1, i)
                        f[i] = min(f[i], f[j] + 1)
        
        return f[n - 1]

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        # 动态规划
        dic, res = dict(), 0
        for num in nums:
            if num not in dic:
                left, right = dic.get(num - 1, 0), dic.get(num + 1,0)
                cur = 1 + left +right
                if res < cur:
                    res = cur
                dic[num] = cur
                dic[num - left] = cur
                dic[num + right] = cur
        return res

5.3 打家劫舍问题

5.4 股票问题

动态规划：121.买卖股票的最佳时机(opens new window) 股票只能买卖一次，问最大利润
动态规划：122.买卖股票的最佳时机II(opens new window) 可以多次买卖股票，问最大收益。
动态规划：123.买卖股票的最佳时机III(opens new window) 最多买卖两次，问最大收益。
动态规划：188.买卖股票的最佳时机IV(opens new window) 最多买卖k笔交易，问最大收益。
动态规划：309.最佳买卖股票时机含冷冻期(opens new window) 可以多次买卖但每次卖出有冷冻期1天。
动态规划：714.买卖股票的最佳时机含手续费(opens new window) 可以多次买卖，但每次有手续费。

5.5 编辑距离问题

判断子序列

动态规划：392.判断子序列 (opens new window)给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

这道题目其实是可以用双指针或者贪心的的，但是我在开篇的时候就说了这是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

状态转移方程：

1 2	if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; else dp[i][j] = dp[i][j - 1];

不同的子序列

动态规划：115.不同的子序列 (opens new window)给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

本题虽然也只有删除操作，不用考虑替换增加之类的，但相对于动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了。

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为 dp[i - 1] [j - 1]

一部分是不用s[i - 1]来匹配，个数为 dp[i - 1] [j]

if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

动态规划：583.两个字符串的删除操作 (opens new window)给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

本题和动态规划：115.不同的子序列 (opens new window)相比，其实就是两个字符串可以都可以删除了，情况虽说复杂一些，但整体思路是不变的。

当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1] [j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1] [j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

动态规划：72.编辑距离 (opens new window)给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

编辑距离终于来了，有了前面三道题目的铺垫，应该有思路了，本题是两个字符串可以增删改，比动态规划：判断子序列 (opens new window)，动态规划：不同的子序列 (opens new window)，动态规划：两个字符串的删除操作 (opens new window)都要复杂的多。

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
- 不操作
if (word1[i - 1] != word2[j - 1])
- 增
- 删
- 换

也就是如上四种情况。

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1] [j - 1]，即dp[i][j] = dp[i - 1] [j - 1];

在整个动规的过程中，最为关键就是正确理解dp[i] [j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 i-1为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i - 1] [j] + 1;

操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个增加元素的操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是添加元素，删除元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word2添加一个元素d，也就是相当于word1删除一个元素d，操作数是一样！

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1] [j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i] [j] = min({dp[i - 1] [j - 1], dp[i - 1] [j], dp[i][j - 1]}) + 1;

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

==让字符串成为最小回文==

https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/

六、回溯法

一个决策树的遍历过程（回溯法）：一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会通过在上一步进行一些变化抛弃该解，即回溯并且再次尝试。

回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

算法长征（11）动态规划

发表于 2021-05-07 更新于 2022-06-27 分类于【draft】工程，数据结构本文字数： 14k 阅读时长 ≈ 25 分钟

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

5.1 背包问题

https://leetcode-cn.com/problems/coin-change/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-wan-q-80r7/

1、确定dp数组以及下标的含义

2、确定递推公式

3、dp数组如何初始化

最大长度

递推等号左侧要初始化

4、确定遍历顺序

滚动数组

5、举例推导dp数组

5.1.1 背包递推公式

问==能否装满背包==（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

==问装满背包有几种方法==：dp[j] += dp[j - nums[i]] ，对应题目如下：

动态规划：494.目标和(opens new window)

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        # 背包问题
        total, n = sum(nums), len(nums)
        if total % 2 != 0:
            return False
        target = total // 2
        dp = [True] + [False] * target
        for i in range(n):
            for j in range(target, nums[i] - 1, -1):
                """
                逆序更新
                dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i]]
                """
                dp[j] |= dp[j - nums[i]]
        return dp[-1]

动态规划：518. 零钱兑换 II(opens new window)
动态规划：377.组合总和Ⅳ(opens new window)

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。
动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满==最大价值==：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

动态规划：474.一和零

问装满背包所有物品的==最小个数==：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

5.1.2 遍历顺序

01背包

一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的，大家需要注意！

完全背包

说完01背包，再看看完全背包。

但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求==组合数==就是外层for循环遍历物品，内层for遍历背包。

如果==求排列数==就是外层for遍历背包，内层for循环遍历物品。

5.2 子序列（数组）问题

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp = [0 for _ in range(len(nums))]
        dp[0] = nums[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1] + nums[i], nums[i])
        return max(dp)

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

动态规划 位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
贪心 + 二分查找 tail[i] : 记录i长度的末尾是什么

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        dp = [1] * len(nums)
        result = 0
        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[j] < numa[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
            result = max(result, dp[i]) #取长的子序列
        return result
     def lengthOfLIS(self, nums: List[int]) -> int:
        # 贪心 + 二分查找 tail[i] : 记录i长度的末尾是什么
        tails, res = [0] * len(nums), 0
        for num in nums:
            i = bisect.bisect_left(tails[:res], num)
            """左边界
            while i < j:
                mid = (i + j)//2
                if tails[m] < num:
                    i = m + 1 
                else:
                    j = m
            """
            tails[i] = num
            if i == res:
                res += 1
        return res

def lenLongestFibSubseq(self, A: List[int]) -> int:
    # 基本顺序是 k，i，j 或者 A[k] = A[j] - A[i]
    n = len(A)
    dic = {}
    # 创建索引字典，提速
    for ind,val in enumerate(A):
        dic[val] = ind
    # 初始化，行代表的是i，不需要取到n-1，为了给j留出位置
    # 初始为2，只要包含了 j i 位置，则意味着已经有了2个数字。
    dp = [[2]*n for _ in range(n-1)]
    ret = 0
    # 因此i只能取到n-2，给j留出空间
    for i in range(1,n-1):
        # j从i+1开始，毕竟j在i后面
        for j in range(i+1,n):
            diff = A[j] - A[i]
            if diff in dic and dic[diff] < i:
                k = dic[diff]
                dp[i][j] = dp[k][i] + 1 # 这个1，代表着k位置数字
                ret = max(ret,dp[i][j])
    return ret

class Solution:
    def findLength(self, A: List[int], B: List[int]) -> int:
        dp = [0] * (len(B) + 1)
        result = 0
        for i in range(1, len(A)+1):
            for j in range(len(B), 0, -1):
                if A[i-1] == B[j-1]:
                    dp[j] = dp[j-1] + 1
                else:
                    dp[j] = 0 #注意这里不相等的时候要有赋0的操作
                result = max(result, dp[j])
        return result

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m, n = len(text1), len(text2)
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[m][n]

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 最长子序列 
        m, n = len(text1), len(text2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, n+1):
                if text2[j-1] == text1[i-1]:
                    dp[i][j] = dp[i-1][j-1] +1 
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

动态规划：最大子序和【贪心】【动态规划】

def maxSubArray(self, nums: List[int]) -> int:
    # 为什么dp[-1]不是最大？需要res
    # dp[i] 以i结尾的最大子数组和
    n = len(nums)
    if n == 0:
        return 0
    dp = [0] * (n)
    dp[0] = nums[0]
    for i in range(1, n):
        dp[i] = max(dp[i-1]+nums[i], nums[i])
    return max(dp)

动态规划：判断子序列【双指针】

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        n, m = len(s), len(t)
        i = j = 0
        while i < n and j < m:
            if s[i] == t[j]:
                i += 1
            j += 1
        return i == n

动态规划：不同的子序列

动态规划：两个字符串的删除操作

# dp[i][j] : word1[i-1], word1[j-1] 最少步数
# word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况 *  min(dp[i-1][j], dp[i][j-1])+1  
  def minDistance(self, word1: str, word2: str) -> int:
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in range(m+1)]
        for i in range(n+1):
            dp[0][i] = i
        for j in range(m+1):
            dp[j][0] = j
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1])+1 # , dp[i-1][j-1]+1
        return dp[-1][-1]

动态规划：编辑距离

为了绝杀编辑距离，我做了三步铺垫，你都知道么？

给定一个字符串 s ，请计算这个字符串中有多少个回文子字符串。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

动态规划、双指针+中心扩展、==Manacher算法==

class Solution:
    def countSubstrings(self, s: str) -> int:
        # 双指针+中心扩散
        result = 0
        def _extend(s, i, j, n):
            res = 0
            while i >= 0 and j < n and s[i] == s[j]: # 确定中心点
                i -= 1
                j += 1
                res += 1 # 扩散过程也是答案
            return res
        for i in range(len(s)):
            result += _extend(s, i, i, len(s)) #以i为中心
            result += _extend(s, i, i+1, len(s)) #以i和i+1为中心
        return result

    def countSubstrings(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 是否为回文子串
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 
        n = len(s)
        dp = [[False] * (n) for _ in range(n)]
        ans = 0
        for i in range(n-1,-1,-1):
            for j in range(i,n):
                if s[i] == s[j]:
                    if j - i <= 1:
                        ans += 1
                        dp[i][j] = True
                    elif dp[i+1][j-1]:
                        ans += 1
                        dp[i][j] = True
        return ans

最长回文子串 ==[Manacher 算法]==

# 中心扩展法
class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 枚举+中心扩展法
        def extendCenter(left, right):
            while 0 <= left and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            # 返回的为while不成立的值
            return left+1, right-1 
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = extendCenter(i,i)
            left2, right2 = extendCenter(i,i+1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start:end+1]

def longestPalindrome(self, s: str) -> str:
    # dp[i][j]: 是否是回文 dp[i+1][j-1] -> dp[i][j]
    # 返回的子串，不是数字 不能记录长度
    n = len(s)
    dp = [[False] * n for _ in range(n)] # 右上为1
    for i in range(n):
        dp[i][i] = True
    begin = 0
    maxlen = 0
    # 判断是否是回文子串中，如果是则记录begin and len
    for i in range(n-1, -1,-1):
        for j in range(i,n):
            if s[i] == s[j]:
                if j - i <=1:
                    dp[i][j] = True
                elif dp[i+1][j-1]:
                    dp[i][j] = True
            
            if dp[i][j] and j - i + 1 > maxlen:
                maxlen = j - i + 1
                begin = i

    return s[begin:begin+maxlen]

Manacher 算法：Manacher 算法是在线性时间内求解最长回文子串的算法。在本题中，我们要求解回文串的个数，为什么也能使用 Manacher 算法呢？这里我们就需要理解一下 Manacher 的基本原理。
- 奇偶长度处理： abaaabaa 会被处理成 #a#b#a#a##a#b#a#a#
- ==$f(i)$ 来表示以 s 的第 i 位为回文中心，可以拓展出的最大回文半径（包括 # ）==，那么$ f(i) - 1$就是以 i 为中心的最大回文串长度。
- 利用已经计算出来的状态来更新 f(i）：回文右端点rm ：i + f(i) - 1

动态规划：最长回文子序列

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # 动态规划 dp[i][j]: s[i:j] 最大回文长度
        # dp[i+1][j-1] -> dp[i][j] 遍历顺序 and j - i >=2
        n = len(s)
        dp = [[0] * i +[1] * (n-i) for i in range(n)] # 从定义出发 右上三角 = 1 有意义
        for i in range(n-1,-1,-1):
            for j in range(i+1,n): # j - i >=2
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2 
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])                
        return dp[0][n-1]

class Solution:
    def minCut(self, s: str) -> int:
        # 动态规划1:判断回文
        n = len(s)
        g = [[True] * n for _ in range(n)]

        for i in range(n - 1, -1, -1):
            for j in range(i + 1, n):
                g[i][j] = (s[i] == s[j]) and g[i + 1][j - 1]
        # 
        f = [float("inf")] * n
        for i in range(n):

            if g[0][i]:
                f[i] = 0
            else:
                for j in range(i):
                    if g[j + 1][i]:
                        # （0, j) + (j+1, i)
                        f[i] = min(f[i], f[j] + 1)
        
        return f[n - 1]

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        # 动态规划
        dic, res = dict(), 0
        for num in nums:
            if num not in dic:
                left, right = dic.get(num - 1, 0), dic.get(num + 1,0)
                cur = 1 + left +right
                if res < cur:
                    res = cur
                dic[num] = cur
                dic[num - left] = cur
                dic[num + right] = cur
        return res

5.3 打家劫舍问题

5.4 股票问题

股票问题总结

动态规划：121.买卖股票的最佳时机(opens new window)

股票只能买卖一次，问最大利润

动态规划、贪心算法

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
      	# 动态规划
        if not prices:
            return 0
        dp = [[0] * 2 for _ in range(len(prices))] 
        dp[0][0] = -prices[0]# 已持有的状态
        dp[0][1] = 0 # 未持有的状态
        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i-1][0], -prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]
    def maxProfit(self, prices: List[int]) -> int:
        # 贪心算法
        if not prices:
            return 0
        buy, profit = prices[0], 0
        for i in range(1, len(prices)):
            profit = max(profit, prices[i] - buy)
            if prices[i] < buy:
                buy = prices[i]
        return profit

动态规划：122.买卖股票的最佳时机II(opens new window) 可以多次买卖股票，问最大收益。

动态规划：123.买卖股票的最佳时机III(opens new window) 最多买卖两次，问最大收益。

动态规划：188.买卖股票的最佳时机IV(opens new window) 最多买卖k笔交易，问最大收益。

动态规划：309.最佳买卖股票时机含冷冻期(opens new window) 可以多次买卖但每次卖出有冷冻期1天。

动态规划：714.买卖股票的最佳时机含手续费(opens new window) 可以多次买卖，但每次有手续费。

5.5 编辑距离问题

判断子序列

动态规划：392.判断子序列 (opens new window)给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

状态转移方程：

1 2	if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; else dp[i][j] = dp[i][j - 1];

不同的子序列

动态规划：115.不同的子序列 (opens new window)给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

本题虽然也只有删除操作，不用考虑替换增加之类的，但相对于动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了。

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为 dp[i - 1] [j - 1]

一部分是不用s[i - 1]来匹配，个数为 dp[i - 1] [j]

if (s[i - 1] == t[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
    dp[i][j] = dp[i - 1][j];
}

两个字符串的删除操作

本题和动态规划：115.不同的子序列 (opens new window)相比，其实就是两个字符串可以都可以删除了，情况虽说复杂一些，但整体思路是不变的。

当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1] [j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有2种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1] [j] + 1

情况二：删word2[j - 1]，最少操作次数为dp [i] [j - 1] + 1

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}

编辑距离

动态规划：72.编辑距离 (opens new window)给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
- 不操作
if (word1[i - 1] != word2[j - 1])
- 增
- 删
- 换

也就是如上四种情况。

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1] [j - 1]，即dp[i][j] = dp[i - 1] [j - 1];

在整个动规的过程中，最为关键就是正确理解dp[i] [j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

即 dp[i][j] = dp[i - 1] [j] + 1;

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是添加元素，删除元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word2添加一个元素d，也就是相当于word1删除一个元素d，操作数是一样！

即 dp[i][j] = dp[i - 1] [j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i] [j] = min({dp[i - 1] [j - 1], dp[i - 1] [j], dp[i][j - 1]}) + 1;

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

==让字符串成为最小回文==

https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/

请实现一个函数用来匹配包含'. '和''的正则表达式。模式中的字符'.'表示任意一个字符，而' '表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但与"aa.a"和"ab*a"均不匹配。

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        # 【dp含义】dp[i][j] : s[:i - 1] 可以正则匹配 p[:j - 1]
        m, n = len(s), len(p)
        # 【初始化】
        dp = [[False] * (n + 1) for _ in range(m + 1)]
        dp[0][0] = True
        for j in range(2, n + 1, 2):
            dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
        # 【遍历顺序】
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                # 【状态转移推导】
                if p[j - 1] == '*': 
                    if dp[i][j - 2]:
                        dp[i][j] = True
                    elif dp[i - 1][j] and (p[j - 2] == '.' or s[i - 1] == p[j - 2]):
                        dp[i][j] = True
                else:
                    if dp[i-1][j-1] and (p[j - 1] == '.' or s[i - 1] == p[j - 1]):
                        dp[i][j] = True
                
        return dp[-1][-1]

六、其他

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。【求三角矩阵非对角线】

动态规划双向遍历

class Solution:
    def constructArr(self, a: List[int]) -> List[int]:
        b, tmp = [1] * len(a), 1
        for i in range(1, len(a)):
            b[i] = b[i - 1] * a[i - 1] # 下三角
        for i in range(len(a) - 2, -1, -1):
            tmp *= a[i + 1]            # 上三角
            b[i] *= tmp                # 下三角 * 上三角
        return b

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

三指针、优先队列（质数的线性筛算法）

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        # 维护3个 2，3，5的动态个数
        dp = [0] * (n + 1)
        dp[1] = 1
        p2 = p3 = p5 = 1
        for i in range(2, n + 1):
          	# 
            u2, u3, u5 = 2 * dp[p2], 3 * dp[p3], 5 * dp[p5]
            dp[i] = min(u2, u3, u5)
            if dp[i] == u5:
                p5 += 1
            if dp[i] == u3:
                p3 += 1
            if dp[i] == u2:
                p2 += 1
        return dp[-1]
    def nthUglyNumber(self, n: int) -> int:
        if n == 1:
            return 1
        H = [(2, 2), (3, 3), (5, 5)]
        heapify(H)
        for i in range(n - 1):
            num, p = heappop(H)
            heappush(H, (num * 2, 2))
            if p >= 3:
                heappush(H, (num * 3, 3))
                if p >= 5:
                    heappush(H, (num * 5, 5))
        #print(len(H)) #n = 1670时, H长度为162
        return num

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

已知n - 1个骰子的解为f(n - 1), 添加一个骰子，求n个骰子的点数和为x的概率f（n， x）

class Solution:
    def dicesProbability(self, n: int) -> List[float]:
        dp = [1 / 6] * 6
        for i in range(2, n + 1):
            tmp = [0] * (5 * i + 1)
            for j in range(len(dp)):
                for k in range(6): # 防止越界
                    tmp[j + k] += dp[j] / 6
            dp = tmp
        return dp

深度学习-【draft】生成对抗网络

发表于 2020-12-21 更新于 2023-05-01 分类于算法，【draft】深度学习， GAN 本文字数： 2.8k 阅读时长 ≈ 5 分钟

1. 介绍GAN

GAN的基本思想
为什么生成器不自己学？
为什么判别器不自己做?
具体算法
笔记：李宏毅学习笔记30.GAN.01. 李宏毅GAN教程（1）

2. Gan的数学原理（GAN背后的理论）

笔记：李宏毅GAN教程（2）李宏毅学习笔记33.GAN.04.Theory behind GAN

3. Conditional GAN (条件GAN)

笔记：李宏毅GAN教程（5）李宏毅学习笔记31.GAN.02.Conditional Generation by GAN

研讨厅思路：

背景意义

Generative Adversarial Network（GAN）被引次数：26083次

Ian J. Goodfellow:phD

Goodlflow-phD

https://github.com/hindupuravinash/the-gan-zoo

GAN的应用

GAN的原理

调节Generator和Discrimnator的训练次数比。一般来说，Discrimnator要训练的比Genenrator多。比如训练五次Discrimnator，再训练一次Genenrator(WGAN论文是这么干的)。这一条不一定对！

GAN的训练过程

GAN与VAE的比较

GAN的发展

http://nooverfit.com/wp/独家｜gan大盘点，聊聊这些年的生成对抗网络-lsgan-wgan-cgan-info/

10个必读的GAN

WGAN，DCGAN，CGAN,Improved Techniques for Training GANs

优化GAN的方法

（1) 结构上的改进CGAN

（2）除了结构上的改进还有，loss, 模型初始化和权重上的改进

（3）GAN的重要实现

目前各领域最先进的GAN

GAN研究方向汇总（附源码） - 清华阿罗的文章 - 知乎 https://zhuanlan.zhihu.com/p/69305310

Level 0: Definition of GANs

Level	Title	authors	Publication	Links
Beginner	GAN : Generative Adversarial Nets	Goodfellow & et al.	NeurIPS (NIPS) 2014	link
Beginner	GAN : Generative Adversarial Nets (Tutorial)	Goodfellow & et al.	NeurIPS (NIPS) 2016 Tutorial	link
Beginner	CGAN : Conditional Generative Adversarial Nets	Mirza & et al.	-- 2014	link
Beginner	InfoGAN : Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets	Chen & et al.	NeuroIPS (NIPS) 2016

Level 1: Improvements of GANs training

然后看看 loss、参数、权重的改进：

Level	Title	Co-authors	Publication	Links
Beginner	LSGAN : Least Squares Generative Adversarial Networks	Mao & et al.	ICCV 2017	link
Advanced	Improved Techniques for Training GANs	Salimans & et al.	NeurIPS (NIPS) 2016	link
Advanced	WGAN : Wasserstein GAN	Arjovsky & et al.	ICML 2017	link
Advanced	WGAN-GP : improved Training of Wasserstein GANs	2017	link
Advanced	Certifying Some Distributional Robustness with Principled Adversarial Training	Sinha & et al.	ICML 2018	link code

Level 2: Implementation skill

GAN的实现

Title	Co-authors	Publication	Links	size	FID/IS
Keras Implementation of GANs	Linder-Norén	Github	link
GAN implementation hacks	Salimans paper & Chintala	World research	link paper
DCGAN : Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks	Radford & et al.	2015.11-ICLR 2016	link paper	64x64 human
ProGAN:Progressive Growing of GANs for Improved Quality, Stability, and Variation	Tero Karras	2017.10	paper link	1024x1024 human	8.04
SAGAN：Self-Attention Generative Adversarial Networks	Han Zhang & Ian Goodfellow	2018.05	paper link	128x128 obj	18.65/52.52
BigGAN:Large Scale GAN Training for High Fidelity Natural Image Synthesis	Brock et al.	2018.09-ICLR 2019	demo paper link	512x512 obj	9.6/166.3
StyleGAN:A Style-Based Generator Architecture for Generative Adversarial Networks	Tero Karras	2018.12	paper link	1024x1024 human	4.04

GAN的应用 Level 3： GANs Applications

图像翻译 (Image Translation)	超分辨率 (Super-Resolution)	图像上色(Colourful Image Colorization)
图像修复(Image Inpainting)	图像去噪(Image denoising)	交互式图像生成

JS散度在没有重合的时候，是常数log2，分辨不出来

恶意软件的对抗样本综述：

A survey on practical adversarial examples for malware classifiers

ABSTRACT

1 INTRODUCTION

2 BACKGROUND

2.1 Machine learning for malware

2.1.1 Static Features

2.1.2 Dynamic Features

2.2 Adversarial examples

2.2.1 Threat models.

2.2.2 Adversarial malware examples

3 PRACTICAL ATTACKS

3.1 Gradient-driven approaches

3.1.1 Editing bytes and metadata

3.1.2 Code transformations

3.2 Problem-driven approaches

3.2.1 Editing bytes and metadata

3.2.2 Code transformation

4 DISCUSSION

4.1 Challenges

4.1.1 Threat models

4.1.2 Establishing baselines

4.1.3 Dataset

4.1.4 Malware classifiers

4.2 Possible research directions

4.2.1 Defending against practical adversarial malware examples

4.2.2 Relationships between obfuscation and adversarial examples

4.2.3 Integration of static and dynamic analysis techniques

4.3 Other Survey and systematization of knowledge papers

5 CONCLUSION

遗传算法

Functionality-Preserving Black-Box Optimization of Adversarial Windows Malware 2021 TIFS

Abstract：

一、Introduction

二、PROGRAMS AND MALWARE DETECTION

2.1 The Windows Portable Executable (PE) File Format

2.2 Learning-Based Windows Malware Detection

三、BLACK-BOX OPTIMIZATION OF ADVERSARIAL WINDOWS MALWARE

3.1 Functionality-Preserving Manipulations（保留功能的操作）

四、实验

4.1 无攻击时的性能

4.2 攻击评估

4.3 硬标签攻击

4.4 时间分析

4.5 加壳影响

4.6 Evaluation on Antivirus Programs (VirusTotal)

五、RELATED WORK

强化学习[15]

随机算法和遗传算法[13],[14]

GAN[27]

六、CONCLUSION AND FUTURE WORK

Black-Box Adversarial Attacks Against Deep Learning Based Malware Binaries Detection with GAN

摘要：

一、说明

二、背景和相关工作

2.1 针对恶意软件检测的对抗性攻击

2.2 Generative Adversarial Networks (GANs)

三、方法

3.1 问题定义

3.2 GAPGAN：

3.3 Black-box Attacks Strategy

四、实验装置（EXPERIMENTAL SETUP）

4.1 数据集

4.2 Target Black-box Models

五、EXPERIMENTAL RESULTS

5.2 与最新攻击方法的比较

5.3 不同防御方式下的攻击性能

5.4 动态参数的使用效果

六、结论

Dynamic Malware Analysis in the Modern Era—A State of the Art Survey

学习内容：

动态分析的意义：

动态分析的局限性：

说明：

恶意软件分类

ANALYZING MALWARE BEHAVIOR

动态恶意软件分析框架描述

分析技术和学术工具

函数功能分析

Execution Control 执行控制