《流畅的python》阅读笔记 《流畅的python》是一本适合python进阶的书,
里面介绍的基本都是高级的python用法. 对于初学python的人来说,
基础大概也就够用了, 但往往由于够用让他们忘了深入, 去精通.
我们希望全面了解这个语言的能力边界,
可能一些高级的特性并不能马上掌握使用, 因此这本书是工作之余,
还有余力的人来阅读, 我这边就将其有用, 精妙的进阶内容整理出来.
笔记链接 :https://juejin.cn/post/6844903503987474446
《流畅的python》阅读笔记
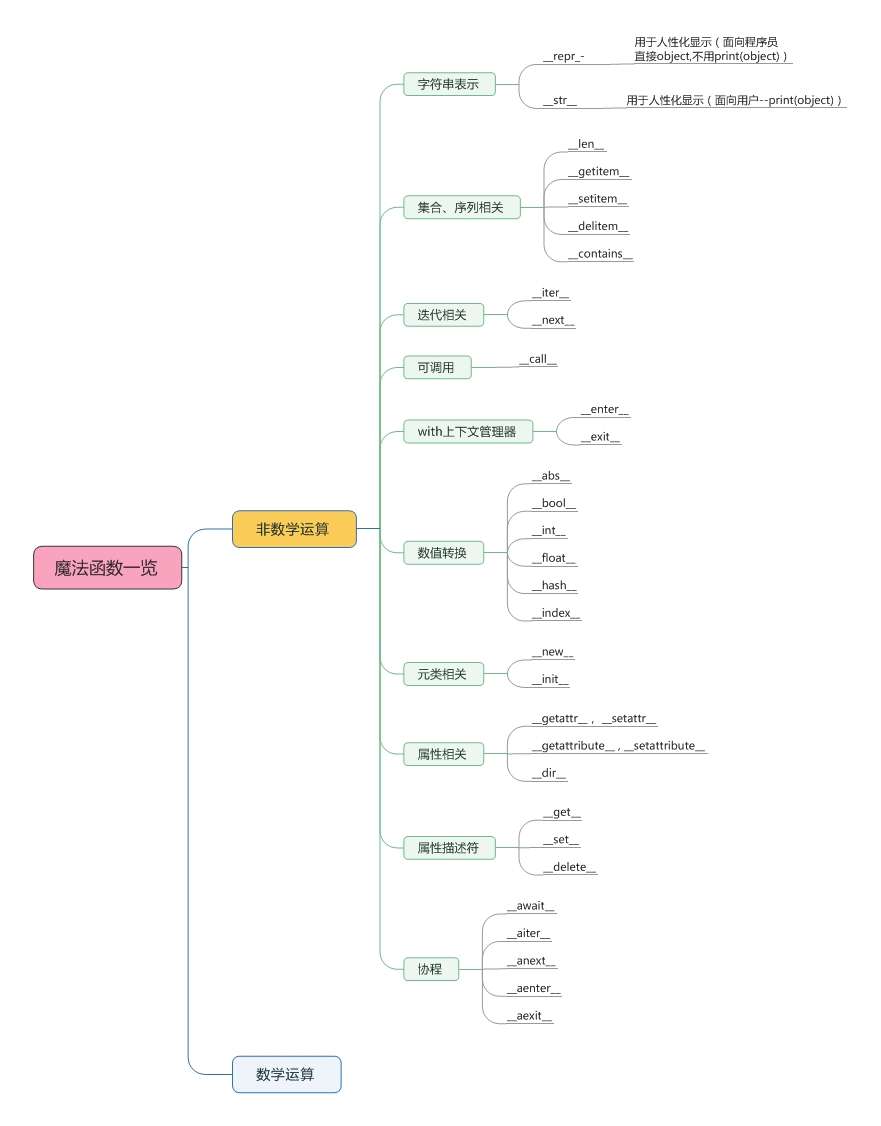
第0章:基础知识 迭代器: 第一章: python数据模型 常用魔法函数: __init__ , __lt__,
__len__,__str__ 与 __repr__ ,
__call__ __iter__
这部分主要介绍了python的魔术方法 ,
它们经常是两个下划线包围来命名的(比如 __init__ ,
__lt__, __len__ ).
这些特殊方法是为了被python解释器调用的,
这些方法会注册到他们的类型中方法集合中 ,
相当于为cpython提供抄近路. 这些方法的速度也比普通方法要快,
当然在自己不清楚这些魔术方法的用途时, 不要随意添加.
关于字符串的表现形式是两种, __str__ 与
__repr__ . python的内置函数 repr 就是通过
__repr__ 这个特殊方法来得到一个对象的字符串表示形式.
这个在交互模式下比较常用, 如果没有实现 __repr__ ,
当控制台打印一个对象时往往是 <A object at 0x000> . 而
__str__ 则是 str() 函数时使用的, 或是在
print 函数打印一个对象的时候才被调用, 终端用户友好.
两者还有一个区别, 在字符串格式化时, "%s" 对应了
__str__ . 而 "%r" 对应了
__repr__. __str__ 和 __repr__
在使用上比较推荐的是,前者是给终端用户看,而后者则更方便我们调试和记录日志.
字符串表示:__str__、__repr__
集合、序列相关:__len__、__getitem__、__setitem__、__delitem__、__contains__
迭代相关:__iter__、__next__
可调用:__call__
with上下文管理器:__enter__、__exit__
属性相关:__getattr__、__setattr__、__getattribute__
第二章: 序列构成的数组 这部分主要是介绍序列 ,
着重介绍数组 和元组 的一些高级用法.
序列按照容纳数据的类型可以分为:
容器序列 : list、tuple 和 collections.deque
这些序列能存放不同类型的数据 。扁平序列 : str、bytes、bytearray、memoryview 和
array.array,这类序列只能容纳一种类型 。
如果按照是否能被修改可以分为:
可变序列 :
list、bytearray、array.array、collections.deque 和 memoryview不可变序列 : tuple、str 和 bytes
列表推导 列表推导是构建列表的快捷方式,
可读性更好且效率更高.
例如, 把一个字符串变成unicode的码 位列表的例子,
一般:
1 2 3 4 symbols = '$¢£¥€¤' codes = [] for symbol in symbols: codes.append(ord (symbol))复制代码
使用列表推导:
1 2 symbols = '$¢£¥€¤' codes = [ord (symbol) for symbol in symbols]复制代码
能用列表推导来创建一个列表, 尽量使用推导, 并且保持它简短.
笛卡尔积与生成器表达式 生成器表达式是能逐个产出元素, 节省内存. 例如:
1 2 3 4 >>> colors = ['black' , 'white' ]>>> sizes = ['S' , 'M' , 'L' ]>>> for tshirt in ('%s %s' % (c, s) for c in colors for s in sizes):... print (tshirt)复制代码
实例中列表元素比较少, 如果换成两个各有1000个元素的列表,
显然这样组合的笛卡尔积是一个含有100万元素的列表, 内存将会占用很大,
而是用生成器表达式就可以帮忙省掉for循环的开销.
具名元组 元组经常被作为 不可变列表 的代表.
经常只要数字索引获取元素, 但其实它还可以给元素命名:
1 2 3 4 5 6 7 8 9 10 11 12 >>> from collections import namedtuple>>> City = namedtuple('City' , 'name country population coordinates' )>>> tokyo = City('Tokyo' , 'JP' , 36.933 , (35.689722 , 139.691667 ))>>> tokyoCity(name='Tokyo' , country='JP' , population=36.933 , coordinates=(35.689722 , 139.691667 ))>>> tokyo.population36.933 >>> tokyo.coordinates(35.689722 , 139.691667 ) >>> tokyo[1 ]'JP'
切片 列表中是以0作为第一个元素的下标, 切片可以根据下标提取某一个片段.
用 s[a:b:c] 的形式对 s 在 a 和
b 之间以 c 为间隔取值。c
的值还可以为负, 负值意味着反向取值.
1 2 3 4 5 6 7 >>> s = 'bicycle' >>> s[::3 ]'bye' >>> s[::-1 ]'elcycib' >>> s[::-2 ]'eccb'
第三章: 字典和集合 dict 类型不但在各种程序里广泛使用, 它也是
Python 语言的基石dict
类型的重要, Python 对其的实现做了高度的优化,
其中最重要的原因就是背后的「散列表」 set(集合)和dict一样,
其实现基础也是依赖于散列表.
散列表也叫哈希表, 对于dict类型, 它的key必须是可哈希的数据类型.
什么是可哈希的数据类型呢, 它的官方解释是:
如果一个对象是可散列的,那么在这个对象的生命周期中,它的散列值是不变
的,而且这个对象需要实现 __hash__()
方法。另外可散列对象还要有 __qe__()
方法,这样才能跟其他键做比较。如果两个可散列对象是相等的,那么它们的散列值一定是一样的……
str, bytes, frozenset 和
数值 都是可散列类型.
字典推导式 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 DIAL_CODE = [ (86 , 'China' ), (91 , 'India' ), (7 , 'Russia' ), (81 , 'Japan' ), ] country_code = {country: code for code, country in DIAL_CODE} print (country_code)''' OUT: {'China': 86, 'India': 91, 'Russia': 7, 'Japan': 81} ''' 复制代码
defaultdict:处理找不到的键的一个选择 当某个键不在映射里, 我们也希望也能得到一个默认值. 这就是
defaultdict , 它是 dict 的子类, 并实现了
__missing__ 方法.
1 2 3 4 5 import collectionsindex = collections.defaultdict(list ) for item in nums: key = item % 2 index[key].append(item)
字典的变种 标准库里 collections 模块中,除了
defaultdict 之外的不同映射类型:
OrderDict :
这个类型在添加键的时候,会保存顺序,因此键的迭代顺序总是一致的ChainMap :
该类型可以容纳数个不同的映射对像,在进行键的查找时,这些对象会被当做一个整体逐个查找,直到键被找到为止
pylookup = ChainMap(locals(), globals())Counter :
这个映射类型会给键准备一个整数技术器,每次更行一个键的时候都会增加这个计数器,所以这个类型可以用来给散列表对象计数,或者当成多重集来用.
1 2 3 4 5 6 import collectionsct = collections.Counter('abracadabra' ) print (ct) ct.update('aaaaazzz' ) print (ct) print (ct.most_common(2 ))
UserDict : 这个类其实就是把标准 dict 用纯 Python
又实现了一遍
1 2 3 4 5 6 7 8 9 10 11 12 import collectionsclass StrKeyDict (collections.UserDict): def __missing__ (self, key ): if isinstance (key, str ): raise KeyError(key) return self[str (key)] def __contains__ (self, key ): return str (key) in self.data def __setitem__ (self, key, item ): self.data[str (key)] = item
不可变映射类型【MappingProxyType】 说到不可变, 第一想到的肯定是元组, 但是对于字典来说,
要将key和value的对应关系变成不可变, types 模块的
MappingProxyType 可以做到:
1 2 3 4 5 6 7 from types import MappingProxyTyped = {1 :'A' } d_proxy = MappingProxyType(d) d_proxy[1 ]='B' d[2 ] = 'B' print (d_proxy)
d_proxy 是动态的, 也就是说对 d
所做的任何改动都会反馈到它上面.
集合论:本身不可散列,元素必须可散列 集合的本质是许多唯一对象的聚集. 因此, 集合可以用于去重.
集合中的元素必须是可散列的 , 但是 set
本身是不可散列的, 而 frozenset 本身可以散列.
集合具有唯一性, 与此同时, 集合还实现了很多基础的中缀运算符.
给定两个集合 a 和 b, a | b 返 回的是它们的合集,
a & b 得到的是交集, 而 a - b
得到的是差集.
合理的利用这些特性, 不仅能减少代码的数量, 更能增加运行效率.
1 2 3 4 5 6 7 8 s = set ([1 , 2 , 2 , 3 ]) s = set () s = {1 , 2 } s = {chr (i) for i in range (23 , 45 )}
第四章: 文本和字节序列 本章讨论了文本字符串 和字节序列 ,
以及一些编码上的转换. 本章讨论的 str 指的是python3下的.
字符问题 字符串是个比较简单的概念: 一个字符串是一个字符序列. 但是关于
"字符" 的定义却五花八门, 其中, "字符"
的最佳定义是 Unicode 字符 . 因此, python3中的
str 对象中获得的元素就是 unicode 字符.
把码位转换成字节序列的过程就是 编码,
把字节序列转换成码位的过程就是 编码 :
1 2 3 4 5 6 7 8 9 >>> s = 'café' >>> len (s)4 >>> b = s.encode('utf8' ) >>> bb'caf\xc3\xa9' >>> len (b)5 >>> b.decode('utf8' )
码位可以认为是人类可读的文本 ,
而字符序列则可以认为是对机器更友好. 所以要区分 .decode() 和
.encode() 也很简单.
从字节序列到人类能理解的文本就是解码(decode).
而把人类能理解的变成人类不好理解的字节序列就是编码(encode).
字节概要 python3有两种字节序列, 不可变的 bytes 类型和可变的
bytearray 类型. 字节序列中的各个元素都是介于
[0, 255] 之间的整数.
处理编码问题 python自带了超过100中编解码器. 每个编解码器都有一个名称,
甚至有的会有一些别名, 如 utf_8 就有 utf8,
utf-8, U8 这些别名.
如果字符序列和预期不符, 在进行解码或编码时容易抛出
Unicode*Error 的异常.
造成这种错误是因为目标编码中没有定义某个字符(没有定义某个码位对应的字符),
这里说说解决这类问题的方式.
使用python3, python3可以避免95%的字符问题.
主流编码尝试下: latin1, cp1252, cp437, gb2312, utf-8, utf-16le
留意BOM头部 b'\xff\xfe' ,
UTF-16编码的序列开头也会有这几个额外字节.
找出序列的编码, 建议使用 codecs 模块
规范化unicode字符串 1 2 s1 = 'café' s2 = 'caf\u00e9' 复制代码
这两行代码完全等价. 而有一种是要避免的是, 在Unicode标准中
é 和 e\u0301 这样的序列叫
"标准等价物".
这种情况用NFC使用最少的码位构成等价的字符串:
1 2 3 4 5 6 7 8 >>> s1 = 'café' >>> s2 = 'cafe\u0301' >>> s1, s2('café' , 'café' ) >>> len (s1), len (s2)(4 , 5 ) >>> s1 s2False 复制代码
改进后:
1 2 3 4 5 6 7 8 9 10 11 12 13 >>> from unicodedata import normalize>>> s1 = 'café' >>> s2 = 'cafe\u0301' >>> len (s1), len (s2)(4 , 5 ) >>> len (normalize('NFC' , s1)), len (normalize('NFC' , s2))(4 , 4 ) >>> len (normalize('NFD' , s1)), len (normalize('NFD' , s2))(5 , 5 ) >>> normalize('NFC' , s1) normalize('NFC' , s2)True >>> normalize('NFD' , s1) normalize('NFD' , s2)True 复制代码
unicode文本排序 对于字符串来说, 比较的码位. 所以在非 ascii 字符时,
得到的结果可能会不尽人意.
第五章: 一等函数 在python中, 函数是一等对象. 编程语言把 "一等对象"
定义为满足下列条件:
在运行时创建
能赋值给变量或数据结构中的元素
能作为参数传给函数
能作为函数的返回结果
在python中, 整数, 字符串, 列表, 字典都是一等对象.
5.1 把函数视作对象 Python即可以函数式编程,也可以面向对象编程. 这里我们创建了一个函数,
然后读取它的 __doc__ 属性, 并且确定函数对象其实是
function 类的实例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def factorial (n ): ''' return n ''' return 1 if n < 2 else n * factorial(n-1 ) print (factorial.__doc__)print (type (factorial))print (factorial(3 ))''' OUT return n <class 'function'> 6 ''' 复制代码
5.2 高阶函数 高阶函数就是接受函数作为参数,
或者把函数作为返回结果的函数 . 如 map,
filter , reduce 等.
比如调用 sorted 时, 将 len
作为参数传递:
1 2 3 fruits = ['strawberry' , 'fig' , 'apple' , 'cherry' , 'raspberry' , 'banana' ] sorted (fruits, key=len )
5.3 匿名函数 lambda 关键字是用来创建匿名函数. 匿名函数一些限制,
匿名函数的定义体只能使用纯表达式. 换句话说, lambda
函数内不能赋值, 也不能使用while和try等语句.
1 2 3 fruits = ['strawberry' , 'fig' , 'apple' , 'cherry' , 'raspberry' , 'banana' ] sorted (fruits, key=lambda word: word[::-1 ])
5.4 可调用对象 除了用户定义的函数, 调用运算符即 ()
还可以应用到其他对象上. 如果像判断对象能否被调用, 可以使用内置的
callable() 函数进行判断.
python的数据模型中有7种可是可以被调用的:
用户定义的函数 : 使用def语句或lambda表达式创建内置函数 :如len内置方法 :如dict.get方法 :在类定义体中的函数类 类的实例 : 如果类定义了 __call__ ,
那么它的实例可以作为函数调用.生成器函数 : 使用 yield
关键字的函数或方法.
5.5 从定位参数到仅限关键字参数 就是可变参数和关键字参数:
1 2 def fun (name, age, *args, **kwargs ): pass 复制代码
其中 *args 和 **kwargs 都是可迭代对象,
展开后映射到单个参数. args是个元组, kwargs是字典 .
第六章 Python设计模式 https://github.com/faif/python-patterns
https://refactoringguru.cn/design-patterns/python
设计模式是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易地被他人理解、保证代码可靠性。
第七章: 函数装饰器和闭包
函数装饰器用于在源码中“标记”函数,以某种方式增强函数的行为。这是一项强大的功能,但是若想掌握,必须理解闭包。
修饰器和闭包经常在一起讨论,
因为修饰器就是闭包的一种形式 .
闭包还是回调式异步编程 和函数式编程风格 的基础.
装饰器基础知识 装饰器 是可调用的对象 ,
其参数是另一个函数 (被装饰的函数).
装饰器可能会处理被装饰的函数, 然后把它返回,
或者将其替换成另一个函数或可调用对象 .
1 2 3 @decorate def target (): print ('running target()' )复制代码
这种写法与下面写法完全等价:
1 2 3 def target (): print ('running target()' ) target = decorate(target)
装饰器是语法糖, 它其实是将函数作为参数让其他函数处理.
装饰器有两大特征:
把被装饰的函数替换成其他函数 装饰器在加载模块时立即执行
要理解立即执行看下等价的代码就知道了,
target = decorate(target) 这句调用了函数.
一般情况下装饰函数都会将某个函数作为返回值.
变量作用域规则 要理解装饰器中变量的作用域, 应该要理解闭包,
我觉得书里将闭包和作用域的顺序换一下比较好. 在python中,
一个变量的查找顺序是 LEGB (L:Local 局部环境,E:Enclosing
闭包,G:Global 全局,B:Built-in 内置).
1 2 3 4 5 6 7 8 9 10 base = 20 def get_compare (): base = 10 def real_compare (value ): base = 5 return value > base return real_compare compare_10 = get_compare() print (compare_10(5 ))复制代码
在闭包的函数 real_compare 中, 使用的变量
base 其实是 base = 10 的.
因为base这个变量在闭包中就能命中, 而不需要去 global
中获取.
闭包 闭包其实挺好理解的, 当匿名函数出现的时候, 才使得这部分难以掌握.
简单简短的解释闭包就是:
名字空间与函数捆绑后的结果被称为一个闭包(closure).
这个名字空间就是 LEGB 中的 E .
所以闭包不仅仅是将函数作为返回值.
而是将名字空间和函数捆绑后作为返回值的. 多少人忘了理解这个
"捆绑" , 不知道变量最终取的哪和哪啊. 哎.
标准库中的装饰器 python内置了三个用于装饰方法的函数: property 、
classmethod 和 staticmethod .
这些是用来丰富类的.
1 2 3 4 class A (object ): @property def age (): return 12
第八章:
对象引用、可变性和垃圾回收 变量不是盒子 很多人把变量理解为盒子, 要存什么数据往盒子里扔就行了.
1 2 3 4 a = [1 ,2 ,3 ] b = a a.append(4 ) print (b)
变量 a 和 b 引用同一个列表,
而不是那个列表的副本.
因此赋值语句应该理解为将变量和值进行引用的关系而已.
标识、相等性和别名 要知道变量a和b是否是同一个值的引用, 可以用
is 来进行判断:
1 2 3 4 5 6 >>> a = b = [4 ,5 ,6 ]>>> c = [4 ,5 ,6 ]>>> a is bTrue >>> x is cFalse 复制代码
如果两个变量都是指向同一个对象, 我们通常会说变量是另一个变量的
别名 .
在 和 is 之间选择 运算符
是用来判断两个对象值是否相等(注意是**对象值**). 而 `is` 则是用于判断两个变量是否指向同一个对象, 或者说判断变量是不是两一个的别名, is 并不关心对象的值. 从使用上,
使用比较多, 而 is 的执行速度比较快.
默认做浅复制 1 2 3 4 5 6 7 8 l1 = [3 , [55 , 44 ], (7 , 8 , 9 )] l2 = list (l1) l2 = l1[:] >>> l2 l1True >>> l2 is l1False 复制代码
尽管 l2 是 l1 的副本, 但是复制的过程是先复制
(即复制了最外层容器 ,副本中的元素是源容器中元素的引用 )
. 因此在操作 l2[1] 时, l1[1] 也会跟着变化.
而如果列表中的所有元素是不可变的, 那么就没有这样的问题,
而且还能节省内存. 但是, 如果有可变元素存在,
就可能造成意想不到的问题.
python标准库中提供了两个工具 copy 和
deepcopy .
分别用于浅拷贝 与深拷贝 :
1 2 3 4 5 import copyl1 = [3 , [55 , 44 ], (7 , 8 , 9 )] l2 = copy.copy(l1) l2 = copy.deepcopy(l1)复制代码
函数的参数做引用时 python中的函数参数都是采用共享传参.
共享传参指函数的各个形式参数获得实参中各个引用的副本. 也就是说,
函数内部的形参是实参的别名.
这种方案就是当传入参数是可变对象时,
在函数内对参数的修改也就是对外部可变对象进行修改.
但这种参数试图重新赋值为一个新的对象时则无效,
因为这只是相当于把参数作为另一个东西的引用, 原有的对象并不变. 也就是说,
在函数内, 参数是不能把一个对象替换成另一个对象的.
不要使用可变类型作为参数的默认值 参数默认值是个很棒的特性. 对于开发者来说,
应该避免使用可变对象作为参数默认值. 因为如果参数默认值是可变对象,
而且修改了它的内容, 那么后续的函数调用上都会收到影响.
del和垃圾回收 在python中, 当一个对象失去了最后一个引用时, 会当做垃圾, 然后被回收掉.
虽然python提供了 del 语句用来删除变量.
但实际上只是删除了变量和对象之间的引用, 并不一定能让对象进行回收,
因为这个对象可能还存在其他引用.
在CPython中,
垃圾回收 主要用的是引用计数 的算法.
每个对象都会统计有多少引用指向自己. 当引用计数归零时,
意味着这个对象没有在使用, 对象就会被立即销毁.【分代垃圾回收算法】
符合Python风格的对象
得益于 Python
数据模型,自定义类型的行为可以像内置类型那样自然。实现如此自然的行为,靠的不是继承,而是鸭子类型 (duck
typing):我们只需按照预定行为实现对象所需的方法即可。
对象表示形式 每门面向对象的语言至少都有一种获取对象的字符串表示形式的标准方式 。Python
提供了两种方式。
repr() :
以便于开发者理解的方式返回对象的字符串表示形式。str() :
以便于用户理解的方式返回对象的字符串表示形式。
classmethod 与 staticmethod 这两个都是python内置提供了装饰器,
一般python教程都没有提到这两个装饰器. 这两个都是在类 class
定义中使用的, 一般情况下, class 里面定义的函数是与其类的实例进行绑定的.
而这两个装饰器则可以改变这种调用方式.
先来看看 classmethod , 这个装饰器不是操作实例的方法,
并且将类本身作为第一个参数. 而 staticmethod
装饰器也会改变方法的调用方式, 它就是一个普通的函数,
classmethod 与 staticmethod 的区别就是
classmethod 会把类本身作为第一个参数传入 ,
其他都一样了.
格式化显示 内置的 format() 函数和 str.format()
方法把各个类型的格式化方式委托给相应的
.__format__(format_spec) 方法. format_spec
是格式说明符,它是:
format(my_obj, format_spec) 的第二个参数str.format() 方法的格式字符串,{}
里代换字段中冒号后面的部分
Python的私有属性和"受保护的"属性 python中对于实例变量没有像 private
这样的修饰符来创建私有属性, 在python中,
有一个简单的机制来处理私有属性.
1 2 3 4 5 6 7 class A : def __init__ (self ): self.__x = 1 a = A() print (a.__x) print (a.__dict__)复制代码
如果属性以 __name 的
两个下划线为前缀, 尾部最多一个下划线 命名的实例属性,
python会把它名称前面加一个下划线加类名, 再放入 __dict__ 中,
以 __name 为例, 就会变成 _A__name .
名称改写算是一种安全措施 , 但是不能保证万无一失,
它能避免意外访问, 但不能阻止故意做坏事.
只要知道私有属性的机制, 任何人都能直接读取和改写私有属性.
因此很多python程序员严格规定:
遵守使用一个下划线标记对象的私有属性 . Python
解释器不会对使用单个下划线的属性名做特殊处理, 由程序员自行控制,
不在类外部访问这些属性. 这种方法也是所推荐的,
两个下划线的那种方式就不要再用了. 引用python大神的话:
绝对不要使用两个前导下划线,这是很烦人的自私行为。如果担心名称冲突,应该明确使用一种名称改写方式(如
_MyThing_blahblah)。这其实与使用双下划线一样,不过自己定的规则比双下划线易于理解。
Python中的把使用一个下划线前缀标记的属性称为"受保护的"属性 。
使用 slots
类属性节省空间 默认情况下, python在各个实例中, 用 __dict__
的字典存储实例属性 . 因此实例的属性是动态变化的,
可以在运行期间任意添加属性. 而字典是消耗内存比较大的结构.
因此当对象的属性名称确定时, 使用 __slots__
可以节约内存.
1 2 3 4 class Vector2d : __slots__ = ('__x' , '__y' ) typecode = 'd'
在类中定义__slots__
属性的目的是告诉解释器:"这个类中的所有实例属性都在这儿了!" 这样,
Python 会在各个实例中使用类似元组的结构存储实例变量,
从而避免使用消耗内存的 __dict__ 属性.
如果有数百万个实例同时活动, 这样做能节省大量内存.
第十五章: 上下文管理器和 else
块 本章讨论的是其他语言不常见的流程控制特性, 正因如此,
python新手往往忽视或没有充分使用这些特性. 下面讨论的特性有:
with 语句和上下文管理器
for while try 语句的 else 子句
with 语句会设置一个临时的上下文,
交给上下文管理器对象控制 ,
并且负责清理上下文 .
这么做能避免错误并减少代码量 ,
因此API更安全 , 而且更易于使用. 除了自动关闭文件之外,
with 块还有其他很多用途.
else 子句先做这个,选择性再做那个的作用.
if语句之外的else块 这里的 else 不是在在 if 语句中使用的, 而是在 for while try
语句中使用的.
1 2 3 4 5 for i in lst: if i > 10 : break else : print ("no num bigger than 10" )
else 子句的行为如下:
for : 仅当 for 循环运行完毕时(即 for
循环没有被 break 语句中止 )才运行 else 块。while : 仅当 while 循环因为条件为假值而退出时(即 while
循环没有被 break 语句中止)才运行 else 块。try : 仅当 try
块中没有异常抛出时 才运行 else 块。
在所有情况下, 如果异常或者 return ,
break 或 continue
语句导致控制权跳到了复合语句的住块外, else
子句也会被跳过.
这一些情况下, 使用 else 子句通常让代码更便于阅读, 而且能省去一些麻烦,
不用设置控制标志作用的变量和额外的if判断.
上下文管理器和with块 上下文管理器对象的目的就是管理 with 语句,
with 语句的目的是简化 try/finally 模式 .
这种模式用于保证一段代码运行完毕后执行某项操作,
即便那段代码由于异常 , return 或者
sys.exit() 调用而终止, 也会执行执行的操作.
finally 子句中的代码通常用于释放重要的资源,
或者还原临时变更的状态.
上下文管理器协议包含 __enter__ 和 __exit__
两个方法. with 语句开始运行时, 会在上下文管理器上调用
__enter__ 方法, 待 with 语句运行结束后, 再调用
__exit__ 方法, 以此扮演了 finally
子句的角色.
with 最常见的例子就是确保关闭文件对象.
上下文管理器调用 __enter__ 没有参数, 而调用
__exit__ 时, 会传入3个参数:
exc_type : 异常类(例如 ZeroDivisionError)exc_value :
异常实例。有时会有参数传给异常构造方法,例如错误消息,这些参数可以使用
exc_value.args 获取traceback : traceback 对象
contextlib模块中的实用工具 在ptyhon的标准库中, contextlib
模块中还有一些类和其他函数,使用范围更广。
closing: 如果对象提供了 close()
方法,但没有实现 __enter__/__exit__
协议,那么可以使用这个函数构建上下文管理器。suppress: 构建临时忽略指定异常的上下文管理器。@contextmanager:
这个装饰器把简单的生成器函数变成上下文管理器,这样就不用创建类去实现管理器协议了。ContextDecorator:
这是个基类,用于定义基于类的上下文管理器。这种上下文管理器也能用于装饰函数,在受管理的上下文中运行整个函数。ExitStack: 这个上下文管理器能进入多个上下文管理器。with
块结束时,ExitStack 按照后进先出的顺序调用栈中各个上下文管理器的
__exit__ 方法。如果事先不知道 with
块要进入多少个上下文管理器,可以使用这个类。例如,同时打开任意一个文件列表中的所有文件。
显然,在这些实用工具中,使用最广泛的是 @contextmanager
装饰器,因此要格外留心。这个装饰器也有迷惑人的一面,因为它与迭代无关,却要使用
yield 语句。
使用@contextmanager @contextmanager
装饰器能减少创建上下文管理器的样板代码量, 因为不用定义
__enter__ 和 __exit__ 方法, 只需要实现一个
yield 语句的生成器.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import sysimport contextlib@contextlib.contextmanager def looking_glass (): original_write = sys.stdout.write def reverse_write (text ): original_write(text[::-1 ]) sys.stdout.write = reverse_write yield 'JABBERWOCKY' sys.stdout.write = original_write with looking_glass() as f: print (f) print ("ABCD" ) 复制代码
yield 语句起到了分割的作用, yield 语句前面的所有代码在
with 块开始时(即解释器调用 __enter__ 方法时)执行, yield
语句后面的代码在 with 块结束时(即调用 __exit__
方法时)执行.
第十六章: 协程 为了理解协程的概念, 先从 yield 来说.
yield item 会产出一个值, 提供给 next(...)
调用方; 此外还会做出让步, 暂停执行生成器, 让调用方继续工作,
直到需要使用另一个值时再调用 next(...)
从暂停的地方继续执行.
从句子语法上看, 协程与生成器类似, 都是通过 yield
关键字的函数. 可是, 在协程中, yield
通常出现在表达式的右边(datum = yield), 可以产出值,
也可以不产出(如果yield后面没有表达式, 那么会产出None).
协程可能会从调用方接收数据, 不过调用方把数据提供给协程使用的是
.send(datum) 方法. 而不是 next(...) . 通常,
调用方会把值推送给协程.
生成器调用方是一直索要数据, 而协程这是调用方可以想它传入数据,
协程也不一定要产出数据.
不管数据如何流动, yield 都是一种流程控制工具,
使用它可以实现写作式多任务: 协程可以把控制器让步给中心调度程序,
从而激活其他的协程.
生成器如何进化成协程 协程的底层框架实现后, 生成器API中增加了 .send(value)
方法. 生成器的调用方可以使用 .send(...) 来发送数据,
发送的数据会变成生成器函数中 yield 表达式的值. 因此,
生成器可以作为协程使用. 除了 .send(...) 方法, 还添加了
.throw(...) 和 .close() 方法,
用来让调用方抛出异常 和终止生成器 .
用作协程的生成器的基本行为
优势:
一个线程中运行,非抢占式的
无需使用实例属性或者闭包, 在多次调用之间都能保持上下文
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 >>> def simple_coroutine ():... print ('-> coroutine started' )... x = yield ... print ('-> coroutine received:' , x)... >>> my_coro = simple_coroutine()>>> my_coro<generator object simple_coroutine at 0x100c2be10 > >>> next (my_coro)-> coroutine started >>> my_coro.send(42 )-> coroutine received: 42 Traceback (most recent call last): ... StopIteration
在 yield 表达式中, 如果协程只需从调用那接受数据,
那么产出的值是 None . 与创建生成器的方式一样,
调用函数得到生成器对象. 协程都要先调用 next(...) 函数,
因为生成器还没启动, 没在 yield 出暂定, 所以一开始无法发送数据.
如果控制器流动到协程定义体末尾, 会像迭代器一样抛出
StopIteration 异常.
使用协程的好处是不用加锁, 因为所有协程只在一个线程中运行,
他们是非抢占式的. 协程也有一些状态, 可以调用
inspect.getgeneratorstate(...) 来获得,
协程都是这4个状态中的一种:
'GEN_CREATED' 等待开始执行。'GEN_RUNNING' 解释器正在执行。'GEN_SUSPENDED' 在 yield 表达式处暂停。'GEN_CLOSED' 执行结束。
只有在多线程应用中才能看到这个状态。此外,生成器对象在自己身上调用
getgeneratorstate 函数也行,不过这样做没什么用。
为了更好理解继承的行为, 来看看产生两个值的协程:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 >>> from inspect import getgeneratorstate>>> def simple_coro2 (a ):... print ('-> Started: a =' , a)... b = yield a... print ('-> Received: b =' , b)... c = yield a + b... print ('-> Received: c =' , c)... >>> my_coro2 = simple_coro2(14 )>>> getgeneratorstate(my_coro2) 'GEN_CREATED' >>> next (my_coro2) -> Started: a = 14 14 >>> getgeneratorstate(my_coro2) 'GEN_SUSPENDED' >>> my_coro2.send(28 ) -> Received: b = 28 42 >>> my_coro2.send(99 ) -> Received: c = 99 Traceback (most recent call last): File "<stdin>" , line 1 , in <module> StopIteration >>> getgeneratorstate(my_coro2) 'GEN_CLOSED' 复制代码
关键的一点是, 协程在 yield 关键字所在的位置暂停执行.
对于 b = yield a 这行代码来说,
等到客户端代码再激活协程时才会设定 b 的值 .
这种方式要花点时间才能习惯, 理解了这个, 才能弄懂异步编程中
yield 的作用.
示例:使用协程计算移动平均值 1 2 3 4 5 6 7 8 9 def averager (): total = 0.0 count = 0 average = None while True : term = yield average total += term count += 1 average = total/count复制代码
这是一个动态计算平均值的协程代码, 这个无限循环表明,
它会一直接收值然后生成结果. 只有当调用方在协程上调用
.close() 方法, 或者没有该协程的引用时, 协程才会终止.
协程的好处是, 无需使用实例属性或者闭包,
在多次调用之间都能保持上下文.
使用 yield from yield from 是全新的语法结构. 它的作用比
yield 多很多.
1 2 3 4 5 6 7 8 >>> def gen ():... for c in 'AB' :... yield c... for i in range (1 , 3 ):... yield i... >>> list (gen())['A' , 'B' , 1 , 2 ]复制代码
可以改写成:
1 2 3 4 5 6 >>> def gen ():... yield from 'AB' ... yield from range (1 , 3 )... >>> list (gen())['A' , 'B' , 1 , 2 ]复制代码
在生成器 gen 中使用 yield form subgen() 时,
subgen 会得到控制权, 把产出的值传给 gen 的调用方, 既调用方可以直接调用
subgen. 而此时, gen 会阻塞, 等待 subgen 终止.
yield from x 表达式对 x
对象所做的第一件事是, 调用 iter(x) 获得迭代器. 因此, x
对象可以是任何可迭代对象.
这个语义过于复杂, 来看看作者 Greg Ewing 的解释:
“把迭代器当作生成器使用,相当于把子生成器的定义体内联在 yield from
表达式
中。此外,子生成器可以执行 return 语句,返回一个值,而返回的值会成为
yieldfrom 表达式的值。”
子生成器是从 yield from <iterable> 中获得的生成器.
而后, 如果调用方使用 send() 方法, 其实也是直接传给子生成器.
如果发送的是 None , 那么会调用子生成器的
__next__() 方法. 如果不是 None ,
那么会调用子生成器的 send() 方法. 当子生成器抛出
StopIteration 异常, 那么委派生成器恢复运行.
任何其他异常都会向上冒泡, 传给委派生成器.
生成器在 return expr 表达式中会触发
StopIteration 异常.
第十七章: 使用 futrues包
处理并发 "futures" 是什么概念呢? 期物指一种对象,
表示异步执行的操作. 这个概念是 concurrent.futures 模块和
asyncio 包的基础.
阻塞型I/O和GIL CPython解释器不是线程安全的, 因此有全局解释锁(GIL),
一次只允许使用一个线程执行 python 字节码,
所以一个python进程不能同时使用多个 CPU 核心.
python程序员编写代码时无法控制 GIL, 然而,
在标准库中所有执行阻塞型I/O操作的函数,
在登台操作系统返回结果时都会释放GIL.
这意味着IO密集型python程序能从中受益.
使用concurrent.futures模块启动进程 一个python进程只有一个 GIL. 多个python进程就能绕开GIL,
因此这种方法就能利用所有的 CPU 核心.
concurrent.futures 模块就实现了真正的并行计算, 因为它使用
ProcessPoolExecutor 把工作交个多个python进程处理.
ProcessPoolExecutor 和 ThreadPoolExecutor
类都实现了通用的 Executor 接口, 因此使用
concurrent.futures
能很轻松把基于线程的方案转成基于进程的方案.
1 2 3 4 def download_many (cc_list ): workers = min (MAX_WORKERS, len (cc_list)) with futures.ThreadPoolExecutor(workers) as executor: res = executor.map (download_one, sorted (cc_list))复制代码
改成:
1 2 3 def download_many (cc_list ): with futures.ProcessPoolExecutor() as executor: res = executor.map (download_one, sorted (cc_list))复制代码
ThreadPoolExecutor.__init__ 方法需要
max_workers 参数,指定线程池中线程的数量; 在
ProcessPoolExecutor 类中, 这个参数是可选的.
第十八章: 使用 asyncio
包处理并发
并发是指一次处理多件事。
并行是指一次做多件事。 二者不同,但是有联系。
一个关于结构,一个关于执行。
并发用于制定方案,用来解决可能(但未必)并行的问题。—— Rob Pike Go
语言的创造者之一









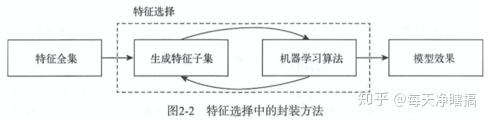
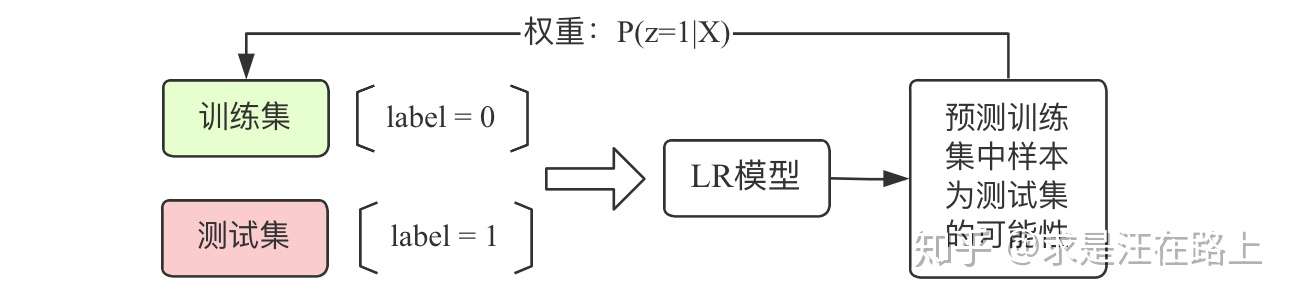
 我们有2种对样本赋权后的模型训练方案,如图2所示。
我们有2种对样本赋权后的模型训练方案,如图2所示。