Pytorch(12)可视化
[PyTorch 学习笔记] 可视化
在 PyTorch 中也可以使用 TensorBoard,具体是使用 TensorboardX 来调用 TensorBoard。除了安装 TensorboardX,还要安装 TensorFlow 和 TensorBoard,其中 TensorFlow 和 TensorBoard 需要一致。
- Captum 【可解释性】: https://captum.ai/docs/introduction
在 PyTorch 中也可以使用 TensorBoard,具体是使用 TensorboardX 来调用 TensorBoard。除了安装 TensorboardX,还要安装 TensorFlow 和 TensorBoard,其中 TensorFlow 和 TensorBoard 需要一致。
- Captum 【可解释性】: https://captum.ai/docs/introduction
这篇文章主要介绍了序列化与反序列化,以及 PyTorch 中的模型保存于加载的两种方式,模型的断点续训练。
模型在内存中是以对象的逻辑结构保存的,但是在硬盘中是以二进制流的方式保存的。
1 | torch.save(obj, f, pickle_module, pickle_protocol=2, _use_new_zipfile_serialization=False) |
主要参数:
其中模型保存还有两种方式:
这种方法比较耗时,保存的文件大
1 | torch.savev(net, path) |
推荐这种方法,运行比较快,保存的文件比较小
1 | state_sict = net.state_dict() |
下面是保存 LeNet 的例子。在网络初始化中,把权值都设置为 2020,然后保存模型。
1 | net = LeNet2(classes=2019) |
运行完之后,文件夹中生成了model.pkl和model_state_dict.pkl,分别保存了整个网络和网络的参数
1 | torch.load(f, map_location=None, pickle_module, **pickle_load_args) |
主要参数:
在训练过程中,可能由于某种意外原因如断点等导致训练终止,这时需要重新开始训练。断点续练是在训练过程中每隔一定次数的 epoch 就保存模型的参数和优化器的参数,这样如果意外终止训练了,下次就可以重新加载最新的模型参数和优化器的参数,在这个基础上继续训练。
下面的代码中,每隔 5 个 epoch 就保存一次,保存的是一个
dict,包括模型参数、优化器的参数、epoch。然后在 epoch
大于 5 时,就break模拟训练意外终止。关键代码如下:
1 | if (epoch+1) % checkpoint_interval == 0: |
在 epoch 大于 5 时,就break模拟训练意外终止
1 | if epoch > 5: |
断点续训练的恢复代码如下:
1 | path_checkpoint = "./checkpoint_4_epoch.pkl" |
需要注意的是,还要设置scheduler.last_epoch参数为保存的
epoch。模型训练的起始 epoch 也要修改为保存的 epoch。
迁移学习:把在 source domain 任务上的学习到的模型应用到 target domain 的任务。
Finetune 就是一种迁移学习的方法。比如做人脸识别,可以把 ImageNet 看作 source domain,人脸数据集看作 target domain。通常来说 source domain 要比 target domain 大得多。可以利用 ImageNet 训练好的网络应用到人脸识别中。
对于一个模型,通常可以分为前面的 feature extractor (卷积层)和后面的 classifier,在 Finetune 时,通常不改变 feature extractor 的权值,也就是冻结卷积层;并且改变最后一个全连接层的输出来适应目标任务,训练后面 classifier 的权值,这就是 Finetune。通常 target domain 的数据比较小,不足以训练全部参数,容易导致过拟合,因此不改变 feature extractor 的权值。
获取预训练模型的参数
使用load_state_dict()把参数加载到模型中
修改输出层
固定 feature extractor 的参数。这部分通常有 2 种做法:
requires_grad=False或者lr=0==params_group给 feature extractor
==设置一个较小的学习率==第一次我们首先不使用 Finetune,而是从零开始训练模型,这时只需要修改全连接层即可:
1 | # 首先拿到 fc 层的输入个数 |
训练了 25 个 epoch 后的准确率为:70.59%。训练的 loss 曲线如下:
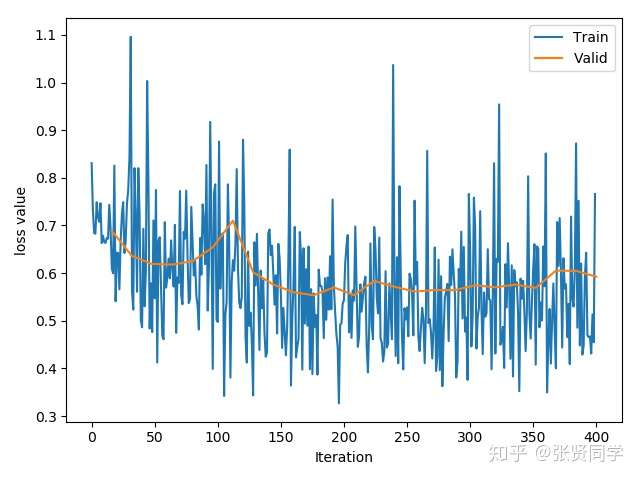
然后我们把下载的模型参数加载到模型中:
1 | path_pretrained_model = enviroments.resnet18_path |
训练了 25 个 epoch 后的准确率为:96.08%。训练的 loss 曲线如下:
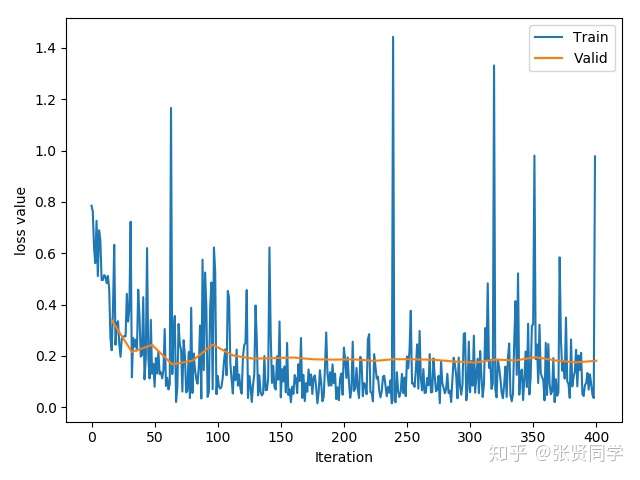
requires_grad=False这里先冻结所有参数,然后再替换全连接层,相当于冻结了卷积层的参数:1 | for param in resnet18_ft.parameters(): |
这里把卷积层的学习率设置为 0,需要在优化器里设置不同的学习率。首先获取全连接层参数的地址,然后使用 filter 过滤不属于全连接层的参数,也就是保留卷积层的参数;接着设置优化器的分组学习率,传入一个 list,包含 2 个元素,每个元素是字典,对应 2 个参数组。其中卷积层的学习率设置为 全连接层的 0.1 倍。
1 | # 首先获取全连接层参数的地址 |
这里不冻结卷积层,而是对卷积层使用较小的学习率,对全连接层使用较大的学习率,需要在优化器里设置不同的学习率。首先获取全连接层参数的地址,然后使用 filter 过滤不属于全连接层的参数,也就是保留卷积层的参数;接着设置优化器的分组学习率,传入一个 list,包含 2 个元素,每个元素是字典,对应 2 个参数组。其中卷积层的学习率设置为 全连接层的 0.1 倍。
1 | # 首先获取全连接层参数的地址 |
下面的代码是使用 Generator 来生成人脸图像,Generator 已经训练好保存在
pkl 文件中,只需要加载参数即可。由于模型是在多 GPU
的机器上训练的,因此加载参数后需要使用remove_module()函数来修改state_dict中的key。
1 | # 多 GPU 的机器上训练模型参数修改 |
在 GAN 的训练模式中,Generator 接收随机数得到输出值,目标是让输出值的分布与训练数据的分布接近,但是这里==不是使用人为定义的损失函数来计算输出值与训练数据分布之间的差异,而是使用 Discriminator 来计算这个差异==。需要注意的是这个差异不是单个数字上的差异,而是分布上的差异。
https://zhuanlan.zhihu.com/p/254738836
在搭建好网络模型之后,一个重要的步骤就是对网络模型中的权值进行初始化。==适当的权值初始化可以加快模型的收敛,而不恰当的权值初始化可能引发梯度消失或者梯度爆炸,最终导致模型无法收敛==。下面分 3 部分介绍。第一部分介绍不恰当的权值初始化是如何引发梯度消失与梯度爆炸的,第二部分介绍常用的 Xavier 方法与 Kaiming 方法,第三部分介绍 PyTorch 中的 10 种初始化方法。
考虑一个 3 层的全连接网络。
,
,
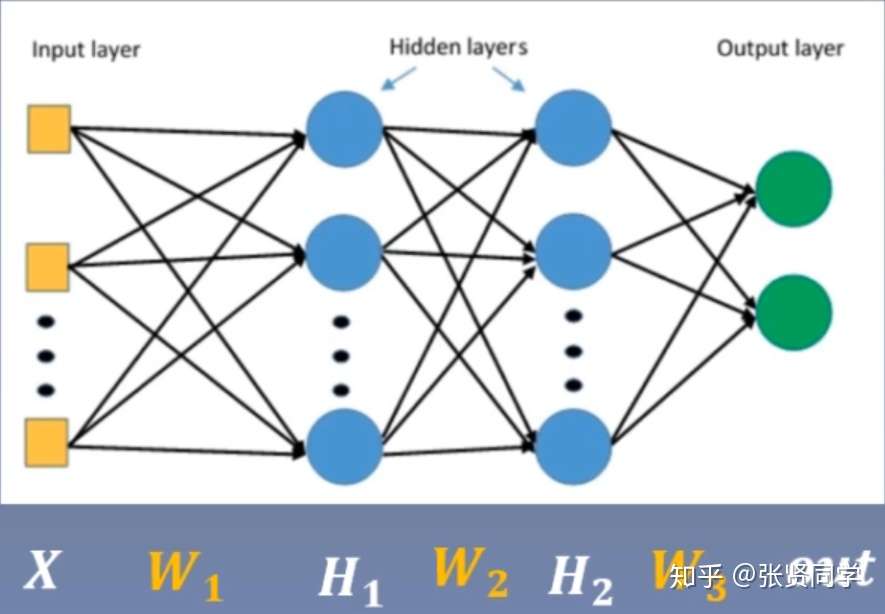
其中第 2 层的权重梯度如下:
所以 依赖于前一层的输出
。如果
趋近于零,那么
也接近于 0,造成梯度消失。如果
趋近于无穷大,那么
也接近于无穷大,造成梯度爆炸。要避免梯度爆炸或者梯度消失,就要严格控制网络层输出的数值范围。
下面构建 100
层全连接网络,先不使用非线性激活函数,每层的权重初始化为服从
的正态分布,输出数据使用随机初始化的数据。
1 | import torch |
输出为:
1 | tensor([[nan, nan, nan, ..., nan, nan, nan], |
也就是==数据太大(梯度爆炸)或者太小(梯度消失)==了。接下来我们在forward()函数中判断每一次前向传播的输出的标准差是否为
nan,如果是 nan 则停止前向传播。
以输入层第一个神经元为例:
其中输入 X 和权值 W 都是服从
的正态分布,所以这个神经元的方差为:
:两个相互独立的随机变量的乘积的期望等于它们的期望的乘积
:一个随机变量的方差等于它的平方的期望减去期望的平方
:两个相互独立的随机变量之和的方差等于它们的方差的和
可以推导出两个随机变量的乘积的方差如下:
![[公式]](https://www.zhihu.com/equation?tex=D%28X+%5Ctimes+Y%29%3DE%5B%28XY%29%5E%7B2%7D%5D+-+%5BE%28XY%29%5D%5E%7B2%7D%3DD%28X%29+%5Ctimes+D%28Y%29+%2B+D%28X%29+%5Ctimes+%5BE%28Y%29%5D%5E%7B2%7D+%2B+D%28Y%29+%5Ctimes+%5BE%28X%29%5D%5E%7B2%7D)
[公式] 如果
,
,那么
标准差为:,所以每经过一个网络层,方差就会扩大 n 倍,标准差就会扩大
倍,n
为每层神经元个数,直到超出数值表示范围。对比上面的代码可以看到,每层神经元个数为
256,输出数据的标准差为 1,所以第一个网络层输出的标准差为 16
左右,第二个网络层输出的标准差为 256 左右,以此类推,直到 31
层超出数据表示范围。可以把每层神经元个数改为 400,那么每层标准差扩大 20
倍左右。从
,可以看出,每一层网络输出的方差与神经元个数、输入数据的方差、权值方差有关,其中比较好改变的是权值的方差
,所以
,标准差为
。
因此修改权值初始化代码为nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))
上述是没有使用非线性变换的实验结果,如果在forward()中添加非线性变换tanh,每一层的输出方差还是会越来越小,会导致梯度消失。因此出现了
Xavier 初始化方法与 Kaiming 初始化方法。
Xavier 是 2010
年提出的,针对有非线性激活函数时的权值初始化方法,目标是保持数据的方差维持在
1 左右,主要针对饱和激活函数如 sigmoid 和 tanh
等。同时考虑前向传播和反向传播,需要满足两个等式: 和
,可得:
。为了使 Xavier 方法初始化的权值服从均匀分布,假设
服从均匀分布
,那么方差
,令
,解得:
,所以
服从分布
所以初始化方法改为:
1 | a = np.sqrt(6 / (self.neural_num + self.neural_num)) |
并且每一层的激活函数都使用 tanh,输出如下:
1 | layer:0, std:0.7571136355400085 |
可以看到每层输出的方差都维持在 0.6 左右。
PyTorch 也提供了 Xavier 初始化方法,可以直接调用:
1 | tanh_gain = nn.init.calculate_gain('tanh') |
#### nn.init.calculate_gain()
上面的初始化方法都使用了
tanh_gain = nn.init.calculate_gain('tanh')。
nn.init.calculate_gain(nonlinearity,param=**None**)的==主要功能是经过一个分布的方差经过激活函数后的变化尺度==,主要有两个参数:
- nonlinearity:激活函数名称
- param:激活函数的参数,如 Leaky ReLU 的 negative_slop。
下面是计算标准差经过激活函数的变化尺度的代码。
2
3
4
5
6
7
8
out = torch.tanh(x)
gain = x.std() / out.std()
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)输出如下:
2
tanh_gain in PyTorch: 1.6666666666666667结果表示,原有数据分布的方差经过 tanh 之后,标准差会变小 1.6 倍左右。
虽然 Xavier 方法提出了针对饱和激活函数的权值初始化方法,但是 AlexNet 出现后,大量网络开始使用非饱和的激活函数如 ReLU 等,这时 Xavier 方法不再适用。2015 年针对 ReLU 及其变种等激活函数提出了 Kaiming 初始化方法。
针对 ReLU,方差应该满足:;针对 ReLu 的变种,方差应该满足:
,a 表示负半轴的斜率,如 PReLU 方法,标准差满足
。代码如下:
nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num)),或者使用
PyTorch
提供的初始化方法:nn.init.kaiming_normal_(m.weight.data),同时把激活函数改为
ReLU。
PyTorch 中提供了 10 中初始化方法
每种初始化方法都有它自己适用的场景,原则是保持每一层输出的方差不能太大,也不能太小。
这篇文章来看下 PyTorch
中网络模型的创建步骤。网络模型的内容如下,包括模型创建和权值初始化,这些内容都在nn.Module中有实现。
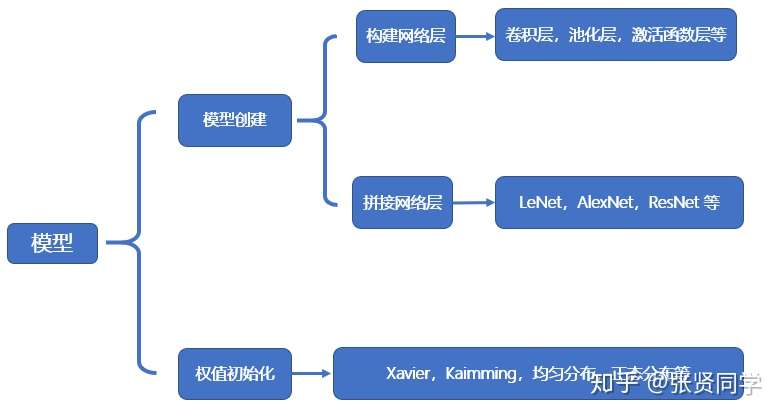
创建模型有 2 个要素:构建子模块和拼接子模块。如 LeNet 里包含很多卷积层、池化层、全连接层,当我们构建好所有的子模块之后,按照一定的顺序拼接起来。
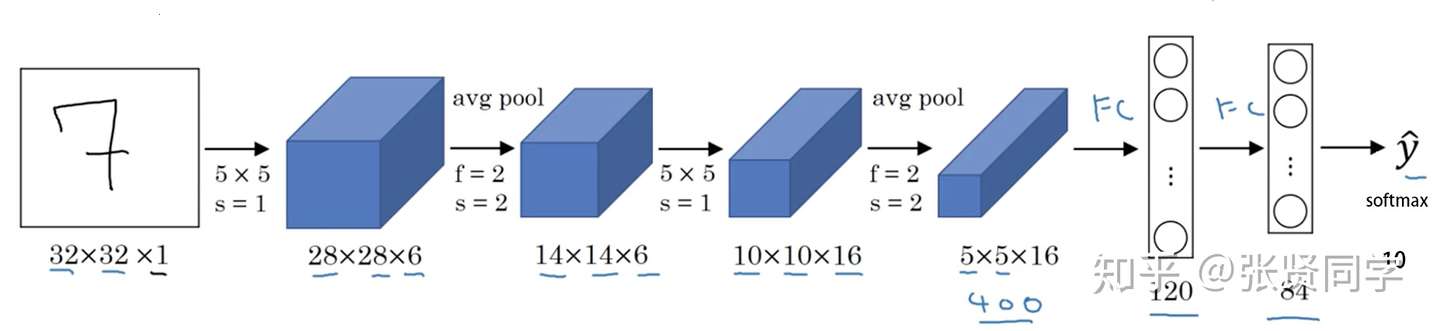
这里以上一篇文章中 lenet.py的 LeNet
为例,继承nn.Module,必须实现__init__()
方法和forward()方法。其中__init__()
方法里创建子模块,在forward()方法里拼接子模块。
1 | class LeNet(nn.Module): |
调用net = LeNet(classes=2)创建模型时,会调用__init__()方法创建模型的子模块。
在训练时调用outputs = net(inputs)时,会进入module.py的call()函数中:
1 | def __call__(self, *input, **kwargs): |
result = self.forward(*input, **kwargs)函数,该函数会进入模型的forward()函数中,进行前向传播。在 torch.nn中包含 4 个模块,如下图所示。

nn.Module 有 8
个属性,都是OrderDict(有序字典)。在 LeNet
的__init__()方法中会调用父类nn.Module的__init__()方法,创建这
8 个属性。
1 | def __init__(self): |
卷积有一维卷积、二维卷积、三维卷积。一般情况下,卷积核在几个维度上滑动,就是几维卷积。比如在图片上的卷积就是二维卷积。
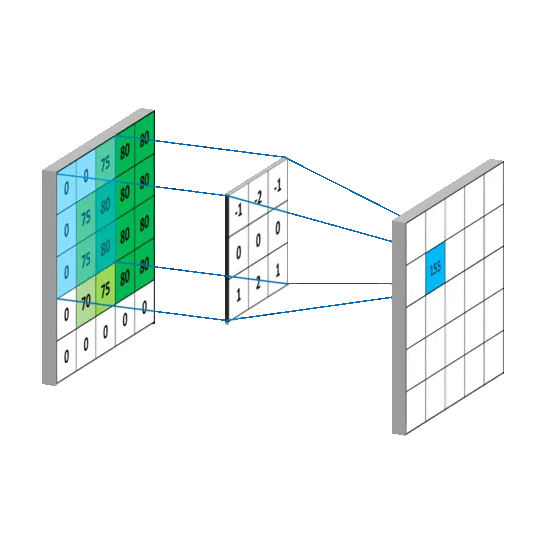
1 | nn.Conv2d(self, in_channels, out_channels, kernel_size, stride=1, |
这个函数的功能是对多个二维信号进行二维卷积,主要参数如下:
这里不考虑空洞卷积,假设输入图片大小为 ,卷积核大小为
,stride 为
,padding
的像素数为
,图片经过卷积之后的尺寸
如下:
下面例子的输入图片大小为 ,卷积大小为
,stride 为 1,padding 为 0,所以输出图片大小为
。
这里使用 input * channel 为 3,output_channel 为 1 ,卷积核大小为
的卷积核 nn.Conv2d(3, 1, 3),使用
nn.init.xavier_normal_()
方法初始化网络的权值。代码如下:
1 | conv_layer = nn.Conv2d(3, 1, 3) |
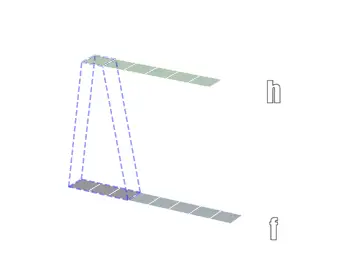
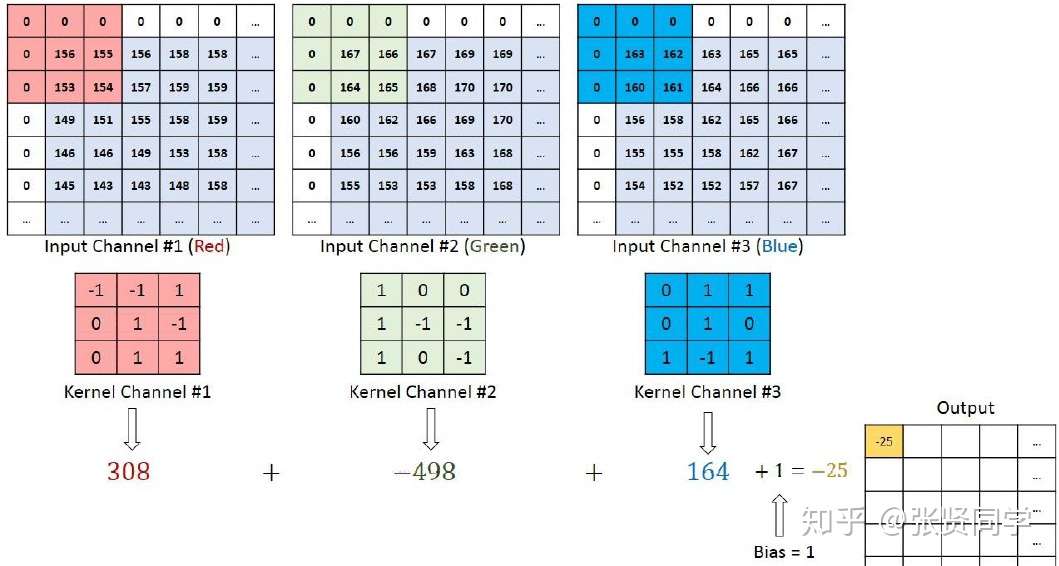
我们通过conv_layer.weight.shape查看卷积核的 shape
是(1, 3, 3, 3),对应是(output_channel, input_channel, kernel_size, kernel_size)。所以第一个维度对应的是卷积核的个数,每个卷积核都是(3,3,3)。虽然每个卷积核都是
3 维的,执行的却是 2 维卷积。下面这个图展示了这个过程。
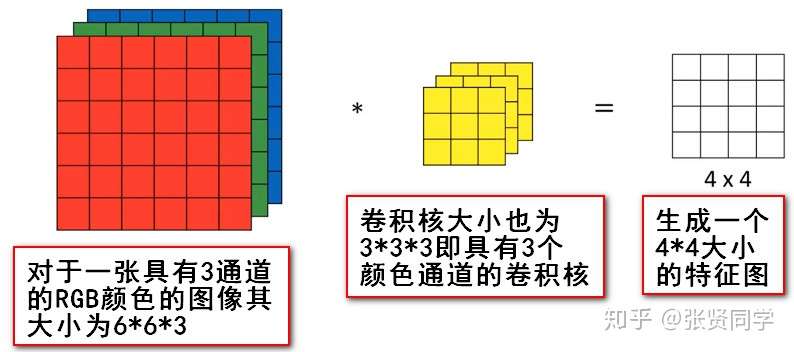
也就是每个卷积核在 input_channel 维度再划分,这里 input_channel 为
3,那么这时每个卷积核的 shape 是(3, 3)。3
个卷积核在输入图像的每个 channel 上卷积后得到 3 个数,把这 3
个数相加,再加上 bias,得到最后的一个输出。
转置卷积又称为反卷积 (Deconvolution) 和部分跨越卷积 (Fractionally strided Convolution),用于对图像进行上采样。
正常卷积如下:

原始的图片尺寸为 ,卷积核大小为
,
,
。由于卷积操作可以通过矩阵运算来解决,因此原始图片可以看作
的矩阵
,卷积核可以看作
的矩阵
,那么输出是
。
转置卷积如下:
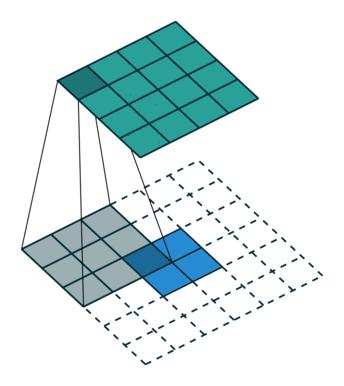
原始的图片尺寸为 ,卷积核大小为
,
,
。由于卷积操作可以通过矩阵运算来解决,因此原始图片可以看作
的矩阵
,卷积核可以看作
的矩阵
,那么输出是
。
正常卷积核转置卷积矩阵的形状刚好是转置关系,因此称为转置卷积,但里面的权值不是一样的,卷积操作也是不可逆的。
PyTorch 中的转置卷积函数如下:
1 | nn.ConvTranspose2d(self, in_channels, out_channels, kernel_size, stride=1, |
和普通卷积的参数基本相同,不再赘述。
这里不考虑空洞卷积,假设输入图片大小为 ,卷积核大小为
,stride 为
,padding
的像素数为
,图片经过卷积之后的尺寸
如下,刚好和普通卷积的计算是相反的:
转置卷积代码示例如下:
1 | import os |
转置卷积前后图片显示如下,左边原图片的尺寸是 (512, 512),右边转置卷积后的图片尺寸是 (1025, 1025)。
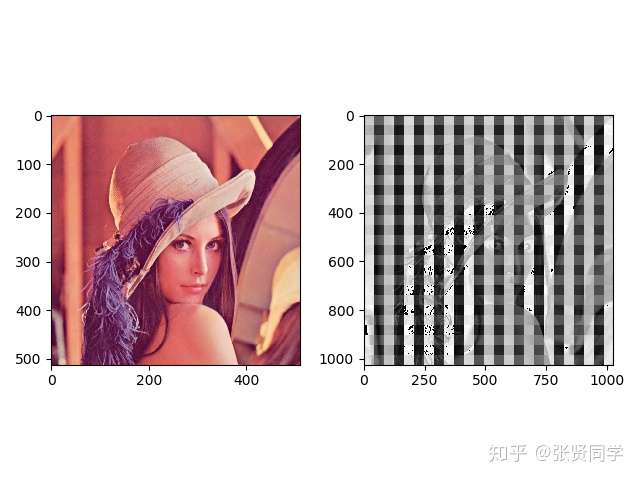
转置卷积后的图片一般都会有棋盘效应,像一格一格的棋盘,这是转置卷积的通病。
关于棋盘效应的解释以及解决方法,推荐阅读Deconvolution And Checkerboard Artifacts[1]。

1 | # 生成器代码 |
1 | class Discriminator(nn.Module): |
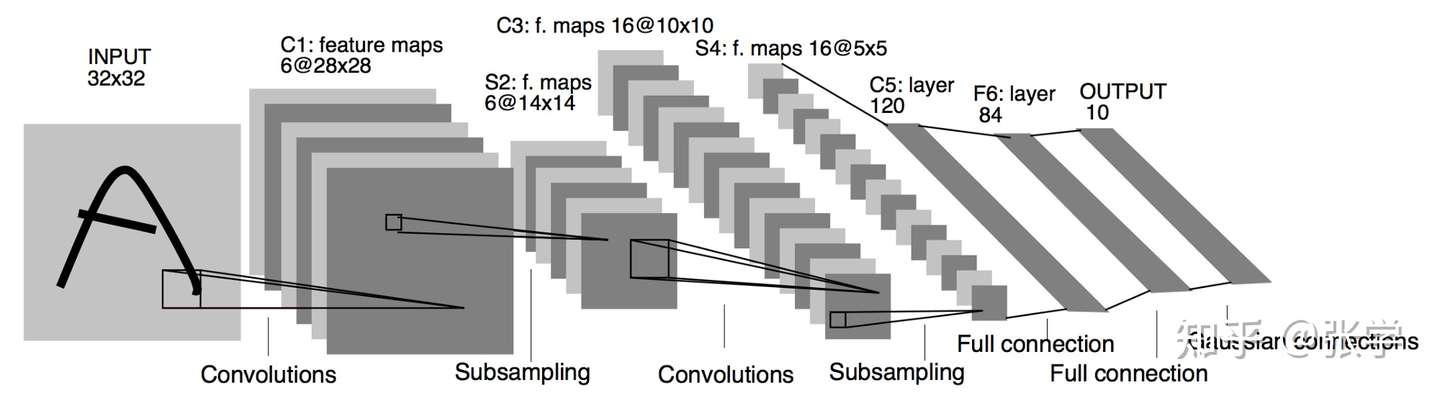
与全连接神经网络不同,卷积神经网络每一层中的节点并不是与前一层的所有神经元节点相连,而是只与前一层的部分节点相连。并且和每一个节点相连的那些通路的权重都是相同的。举例来说,对于二维卷积神经网络,其权重就是卷积核里面的那些值,这些值从上而下,从左到右要将图像中每个对应区域卷积一遍然后将积求和输入到下一层节点中激活,得到下一层的特征图。因此其权重和偏置更新公式与全连接神经网络不通。
根据《Deep learning》这本书的描述,卷积神经网络有3个核心思想:
池化的作用则体现在降采样:保留显著特征、降低特征维度,增大 kernel 的感受野。 另外一点值得注意:pooling 也可以提供一些旋转不变性。 池化层可对提取到的特征信息进行降维,一方面使特征图变小,简化网络计算复杂度并在一定程度上避免过拟合的出现;一方面进行特征压缩,提取主要特征。
1 | nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False) |
这个函数的功能是进行 2 维的最大池化,主要参数如下:
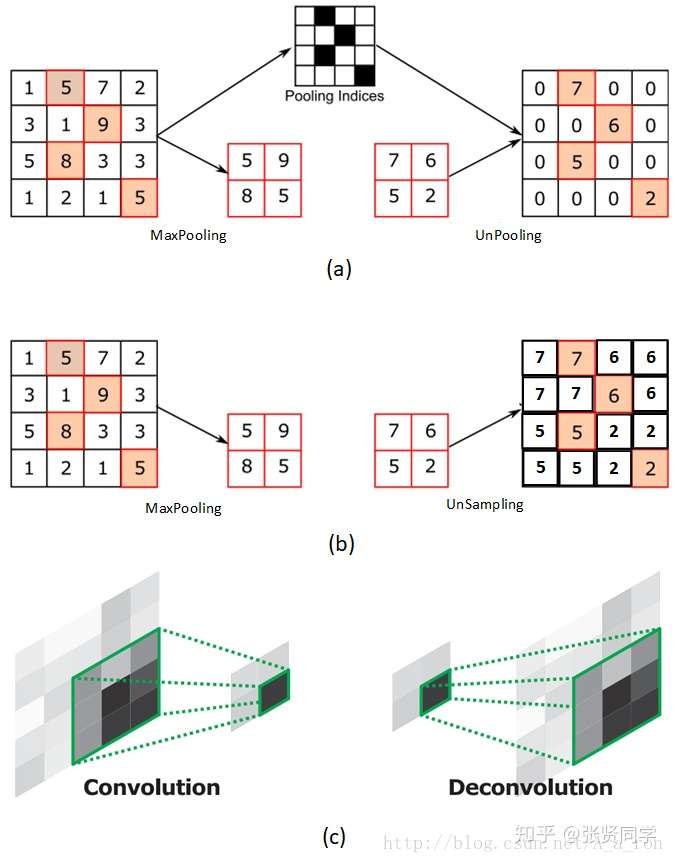
1 | torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None) |
这个函数的功能是进行 2 维的平均池化,主要参数如下:
1 | img_tensor = torch.ones((1, 1, 4, 4)) |
1 | nn.MaxUnpool2d(kernel_size, stride=None, padding=0) |
功能是对二维信号(图像)进行最大值反池化,主要参数如下:
线性层又称为全连接层,其每个神经元与上一个层所有神经元相连,实现对前一层的线性组合或线性变换。
1 | inputs = torch.tensor([[1., 2, 3]]) |
输出为:
1 | tensor([[1., 2., 3.]]) torch.Size([1, 3]) |
假设第一个隐藏层为:,第二个隐藏层为:
,输出层为:
如果没有非线性变换,由于矩阵乘法的结合性,多个线性层的组合等价于一个线性层。激活函数对特征进行非线性变换,赋予了多层神经网络具有深度的意义。下面介绍一些激活函数层。
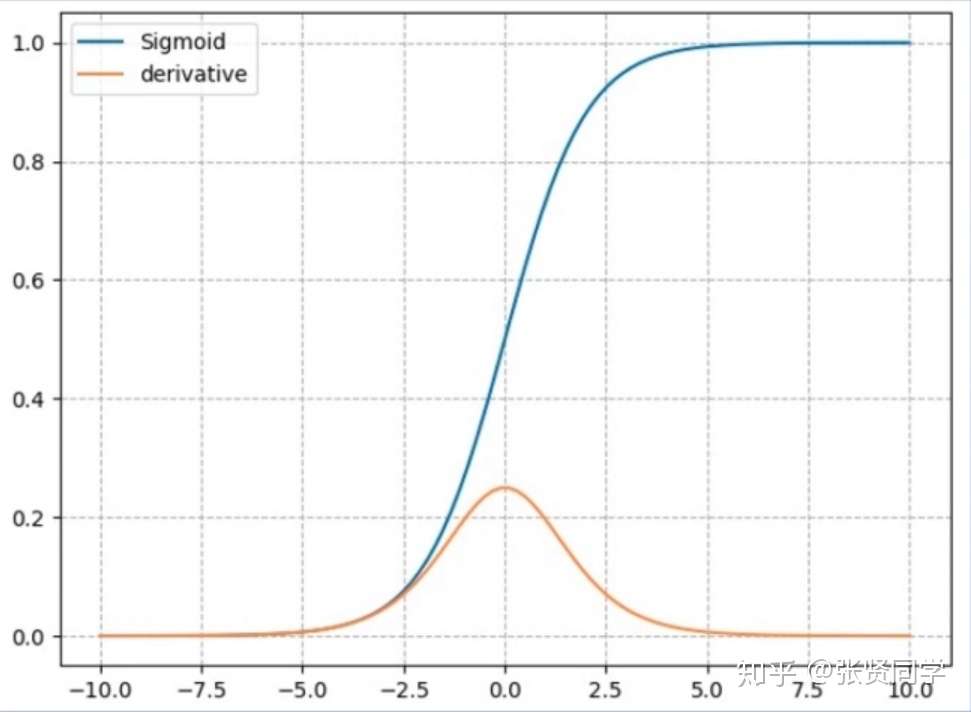
计算公式:
梯度公式:
特性:
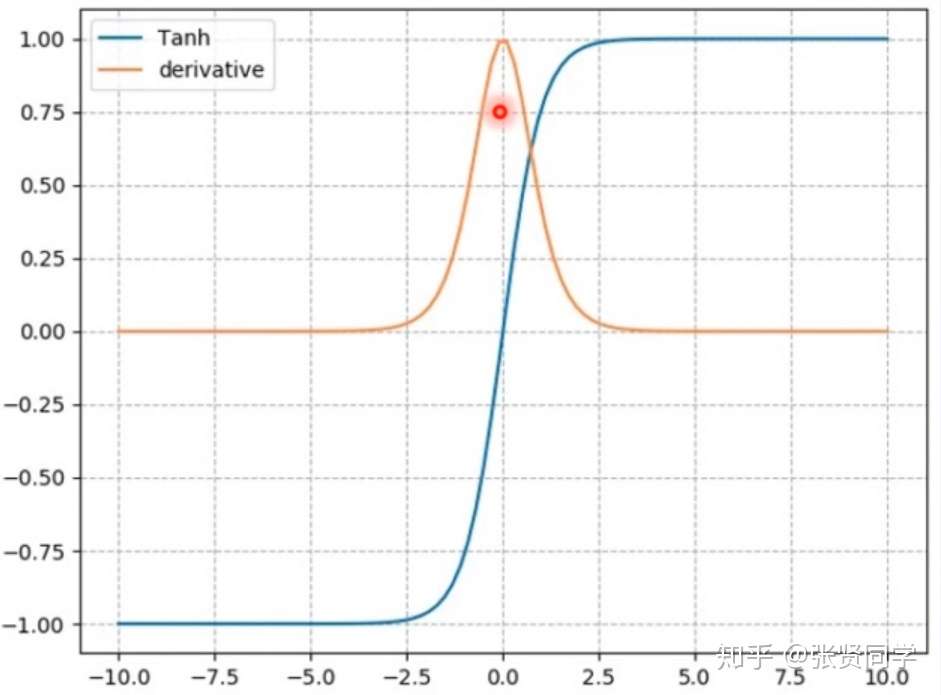
计算公式:
梯度公式:
特性:
计算公式:
梯度公式:
特性:
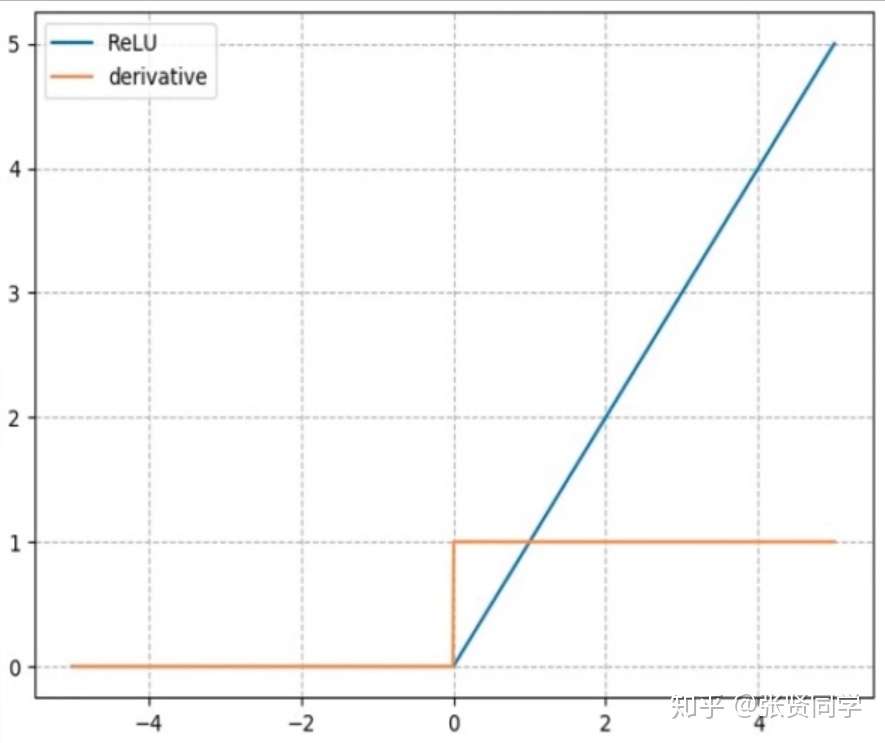
针对 RuLU 会导致==死神经元==的缺点,出现了下面 3 种改进的激活函数。
negative_slope:设置负半轴斜率init:设置初始斜率,这个斜率是可学习的R 是 random 的意思,负半轴每次斜率都是随机取 [lower, upper] 之间的一个数