Self - supervised Learning（BERT-P1）

每个人都应该熟悉监督学习，当我们做监督学习时，我们只有一个模型，这个模型的输入是x，输出是y。假设你今天想做情感分析，你就是让机器阅读一篇文章，而机器需要对这篇文章进行分类，是正面的还是负面的，你必须先找到大量的文章，你需要对所有的文章进行label。我们需要有标签和文章数据来训练监督模型。

"Self-supervised "是用另一种方式来监督，没有标签。假设我们只有一堆没有label的文章，但我们试图找到一种方法把它分成两部分。我们让其中一部分作为模型的输入数据，另一部分作为标签。

Masking Input

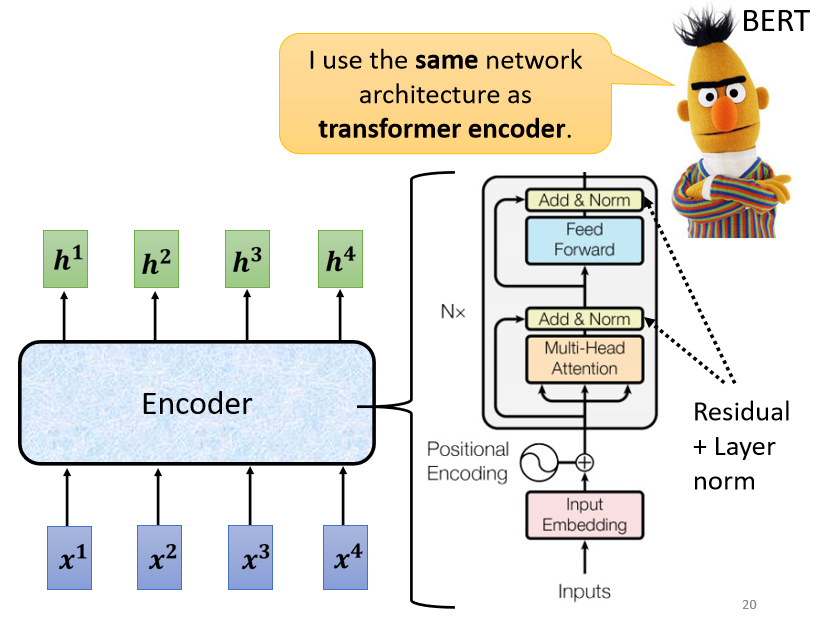
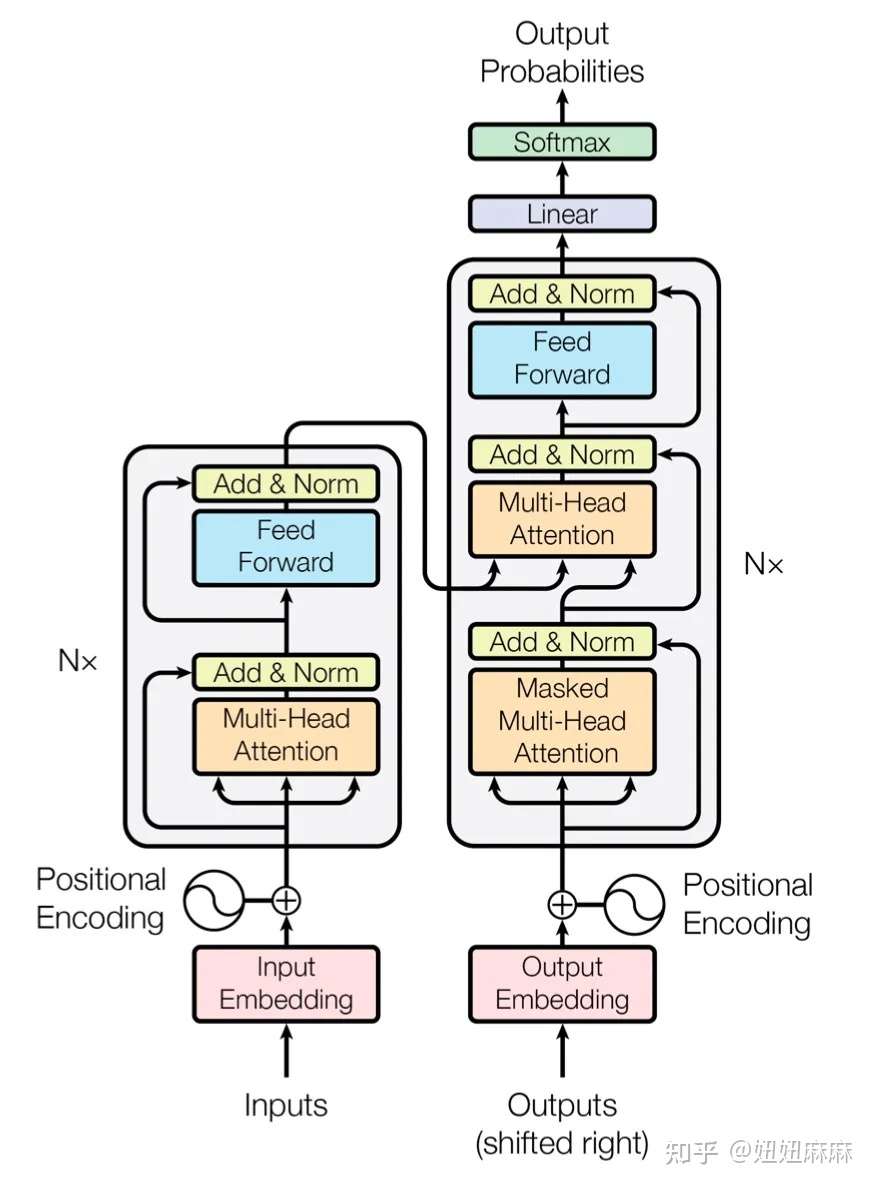
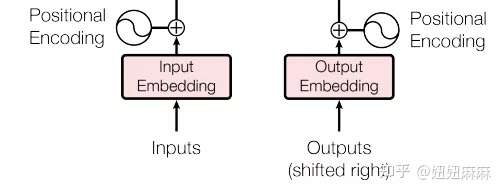
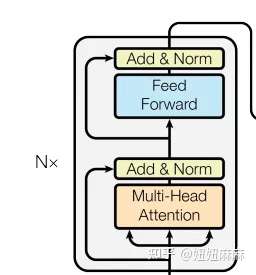
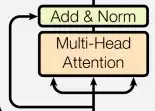
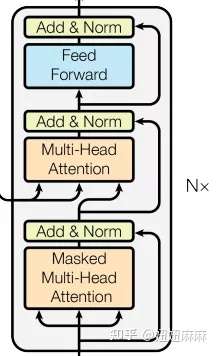
Self-supervised Learning是什么意思呢，我们直接拿BERT模型来说。 BERT是一个transformer的Encoder，我们已经讲过transformer了，我们也花了很多时间来介绍Encoder和Decoder，transformer中的Encoder它实际上是BERT的架构，它和transformer的Encoder完全一样，里面有很多Self-Attention和Residual connection，还有Normalization等等，那么，这就是BERT。

如果你已经忘记了Encoder里有哪些部件，你需要记住的关键点是，BERT可以输入一行向量，然后输出另一行向量，输出的长度与输入的长度相同 。 BERT一般用于自然语言处理，用于文本场景，所以一般来说，它的输入是一串文本，也是一串数据。

当我们真正谈论Self-Attention的时候，我们也说不仅文本是一种序列，而且语音也可以看作是一种序列，甚至图像也可以看作是一堆向量。BERT同样的想法是，不仅用于NLP，或者用于文本，它也可以用于语音和视频。

接下来我们需要做的是，随机盖住一些输入的文字，被mask的部分是随机决定的，例如，我们输入100个token，什么是token？在中文文本中，我们通常把一个汉字看作是一个token，当我们输入一个句子时，其中的一些词会被随机mask。

mask的具体实现有两种方法：

• 第一种方法是，用一个特殊的符号替换句子中的一个词，我们用 "MASK "标记来表示这个特殊符号，你可以把它看作一个新字，这个字完全是一个新词，它不在你的字典里，这意味着mask了原文。
• 另外一种方法，随机把某一个字换成另一个字。中文的 "湾"字被放在这里，然后你可以选择另一个中文字来替换它，它可以变成 "一 "字，变成 "天 "字，变成 "大 "字，或者变成 "小 "字，我们只是用随机选择的某个字来替换它

所以有两种方法来做mask，一种是添加一个特殊的标记 "MASK"，另一种是用一个字来替换某个字。

两种方法都可以使用。使用哪种方法也是随机决定的。因此，当BERT进行训练时，向BERT输入一个句子，先随机决定哪一部分的汉字将被mask。mask后，一样是输入一个序列，我们把BERT的相应输出看作是另一个序列，接下来，我们在输入序列中寻找mask部分的相应输出，然后，这个向量将通过一个==Linear transform==。

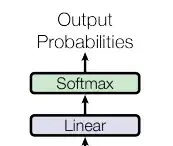
所谓的Linear transform是指，输入向量将与一个矩阵相乘，然后做softmax，输出一个分布。这与我们在Seq2Seq模型中提到的使用transformer进行翻译时的输出分布相同。输出是一个很长的向量，包含我们想要处理的每个汉字，每一个字都对应到一个分数。

在训练过程中。我们知道被mask的字符是什么，而BERT不知道，我们可以用一个one-hot vector来表示这个字符，并使输出和one-hot vector之间的交叉熵损失最小。

或者说得简单一点，我们实际上是在解决一个分类问题。现在，BERT要做的是，预测什么被盖住。被掩盖的字符，属于 "湾"类。在训练中，我们在BERT之后添加一个线性模型，并将它们一起训练。所以，BERT里面是一个transformer的Encoder，它有一堆参数。这两个需要共同训练，并试图预测被覆盖的字符是什么，这叫做mask。

Next Sentence Prediction

事实上，当我们训练BERT时，除了mask之外，我们还会使用另一种方法，这种额外的方法叫做==Next Sentence Prediction== 。

它的意思是，我们从数据库中拿出两个句子，这是我们通过在互联网上抓取和搜索文件得到的大量句子集合，我们在这两个句子之间添加一个特殊标记。这样，BERT就可以知道，这两个句子是不同的句子，因为这两个句子之间有一个分隔符。

我们还将在句子的开头添加一个特殊标记，这里我们用CLS来表示这个特殊标记。

现在，我们有一个很长的序列，包括两个句子，由SEP标记和前面的CLS标记分开。如果我们把它传给BERT，它应该输出一个序列，因为输入也是一个序列，这毕竟是Encoder的目的。我们将只看CLS的输出，我们将把它乘以一个Linear transform。

现在它必须做一个二分类问题，有两个可能的输出：是或不是。这个方法被称为Next Sentence Prediction ，所以我们需要预测，第二句是否是第一句的后续句。

然而，后来的研究发现，对于BERT要做的任务来说，Next Sentence Prediction 并没有真正的帮助。例如，有一篇论文叫 "Robustly Optimized BERT Approach"，简称RoBERTa。在这篇论文中，它明确指出，实施Next Sentence Prediction ，几乎没有任何帮助。然后，这个概念不知不觉地成为主流。

在这之后，另一篇论文说下一句话预测没有用，所以在它之后的许多论文也开始说它没有用。例如，SCAN-BERT和XLNet都说Next Sentence Prediction 方法是无用的。它可能是无用的原因之一是，Next Sentence Prediction 太简单了，是一项容易的任务。

这个任务的典型方法是，首先随机选择一个句子，然后从数据库中或随机选择要与前一个句子相连的句子。通常，当我们随机选择一个句子时，它看起来与前一个句子有很大不同。对于BERT来说，预测两个句子是否相连并不是太难。因此，在训练BERT完成Next Sentence Prediction 的任务时，没有学到什么太有用的东西。

还有一种类似于Next Sentence Prediction 的方法，它在纸面上看起来更有用，它被称为==Sentence order prediction==，简称SOP。

这个方法的主要思想是，我们最初挑选的两个句子可能是相连的。可能有两种可能性：要么句子1在句子2后面相连，要么句子2在句子1后面相连。有两种可能性，我们问BERT是哪一种。

也许因为这个任务更难，它似乎更有效。它被用在一个叫ALBERT的模型中，这是BERT的高级版本。由于ALBERT这个名字与爱因斯坦相似，我在幻灯片中放了一张爱因斯坦的图片。

BERT学了什么？

当我们训练时，我们要求BERT学习两个任务。

• 一个是掩盖一些字符，具体来说是汉字，然后要求它填补缺失的字符。

• 另一个任务表明它能够预测两个句子是否有顺序关系。

所以总的来说，BERT它学会了如何填空。BERT的神奇之处在于，在你训练了一个填空的模型之后，它还可以用于其他任务。这些任务不一定与填空有关，也可能是完全不同的任务，但BERT仍然可以用于这些任务，这些任务是BERT实际使用的任务，它们被称为==Downstream Tasks==(下游任务)，以后我们将谈论一些Downstream Tasks 的例子。

所谓的 "Downstream Tasks "是指，你真正关心的任务。但是，当我们想让BERT学习做这些任务时，我们仍然需要一些标记的信息。

总之，BERT只是学习填空，但是，以后可以用来做各种你感兴趣的Downstream Tasks 。它就像胚胎中的干细胞,它有各种无限的潜力，虽然它还没有使用它的力量,它只能填空,但以后它有能力解决各种任务。我们只需要给它一点数据来激发它，然后它就能做到。

BERT怎么测试性能？

BERT分化成各种任务的功能细胞，被称为==Fine-tune==(微调) 。所以，我们经常听到有人说，他对BERT进行了微调，也就是说他手上有一个BERT，他对这个BERT进行了微调，使它能够完成某种任务，与微调相反，在微调之前产生这个BERT的过程称为==预训练==。所以，生成BERT的过程就是Self-supervised学习。但是，你也可以称之为预训练。

好的，在我们谈论如何微调BERT之前，我们应该先看看它的能力。今天，为了测试Self-supervised学习的能力，通常，你会在多个任务上测试它。因为我们刚才说，BERT就像一个胚胎干细胞，它要分化成各种任务的功能细胞，我们通常不会只在一个任务上测试它的能力，你会让这个BERT分化成各种任务的功能细胞，看看它在每个任务上的准确性，然后我们取其平均值，得到一个总分。这种不同任务的集合，，我们可以称之为任务集。任务集中最著名的基准被称为==GLUE==，它是General Language Understanding Evaluation的缩写。

在GLUE中，总共有9个任务。一般来说，你想知道像BERT这样的模型是否被训练得很好。所以，你实际上会得到9个模型，用于9个单独的任务。你看看这9个任务的平均准确率，然后，你得到一个值。这个值代表这个Self-supervised模型的性能。让我们看看BERT在GLUE上的性能。

有了BERT，GLUE得分，也就是9个任务的平均得分，确实逐年增加。在这张图中，,横轴表示不同的模型，这里列出了，你可以发现，除了ELMO和GPT，其他的还有很多BERT，各种BERT。

黑色的线，表示人类的工作，也就是人类在这个任务上的准确度，那么，我们把这个当作1，这里每一个点代表一个任务，那么，你为什么要和人类的准确度进行比较呢？

人类的准确度是1，如果他们比人类好，这些点的值就会大于1，如果他们比人类差，这些点的值就会小于1，这是因为这些任务，其评价指标可能不是准确度。每个任务使用的评价指标是不同的，它可能不是准确度。如果我们只是比较它们的值，可能是没有意义的。所以，这里我们看的是人类之间的差异。所以，你会发现，在原来的9个任务中，只有1个任务，机器可以比人类做得更好。随着越来越多的技术被提出，越来越多的,还有3个任务可以比人类做得更好。对于那些远不如人类的任务，,它们也在逐渐追赶。

蓝色曲线表示机器GLUE得分的平均值。还发现最近的一些强势模型，例如XLNET，甚至超过了人类。当然，这只是这些数据集的结果，并不意味着机器真的在总体上超过了人类。它在这些数据集上超过了人类。这意味着这些数据集并不能代表实际的表现，而且难度也不够大。所以，在GLUE之后，有人做了Super GLUE。他们找到了更难的自然语言处理任务，让机器来解决。好了！展示这幅图的意义主要是告诉大家，有了BERT这样的技术，机器在自然语言处理方面的能力确实又向前迈进了一步。

How to use BERT

Case 1： Sentiment analysis

第一个案例是这样的，我们假设我们的Downstream Tasks 是输入一个序列，然后输出一个class，这是一个分类问题。比如说 Sentiment analysis 情感分析，就是给机器一个句子，让它判断这个句子是正面的还是负面的。

对于BERT来说，它是如何解决情感分析的问题的？

你只要给它一个句子，也就是你想用它来判断情绪的句子，然后把CLS标记放在这个句子的前面，我刚才提到了CLS标记。 我们把CLS标记放在前面，扔到BERT中,这4个输入实际上对应着4个输出。然后，我们只看CLS的部分。CLS在这里输出一个向量，我们对它进行Linear transform，也就是将它乘以一个Linear transform的矩阵，这里省略了Softmax。

然而，在实践中，你必须为你的Downstream Tasks 提供标记数据，换句话说，BERT没有办法从头开始解决情感分析问题，你仍然需要向BERT提供一些标记数据，你需要向它提供大量的句子，以及它们的正负标签，来训练这个BERT模型。

在训练的时候，Linear transform和BERT模型都是利用Gradient descent来更新参数的。

• Linear transform的参数是随机初始化的
• 而BERT的参数是由学会填空的BERT初始化的。

每次我们训练模型的时候，我们都要初始化参数，我们利用梯度下降来更新这些参数，然后尝试minimize loss，例如，我们正在做情感分类，但是，我们现在有BERT。我们不必随机初始化所有的参数。,我们唯一随机初始化的部分是Linear这里。BERT的骨干是一个巨大的transformer的Encoder。这个网络的参数不是随机初始化的。把学过填空的BERT参数，放到这个地方的BERT中作为参数初始化。

我们为什么要这样做呢？为什么要用学过填空的BERT，再放到这里呢？

最直观和最简单的原因是，它比随机初始化新参数的网络表现更好。当你把学会填空的BERT放在这里时，它将获得比随机初始化BERT更好的性能。

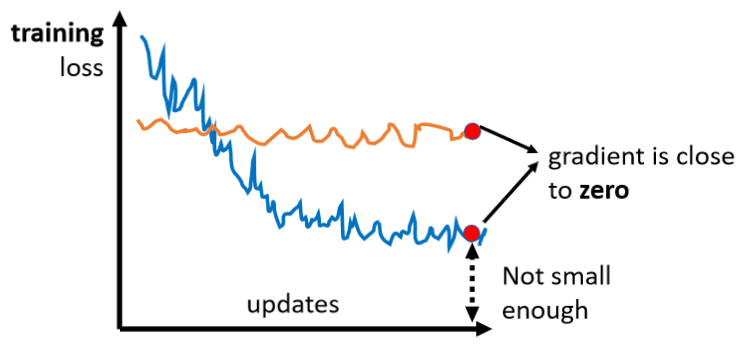
在这里有篇文章中有一个例子。横轴是训练周期，纵轴是训练损失，到目前为止，大家对这种图一定很熟悉，随着训练的进行，损失当然会越来越低，这个图最有趣的地方是，有各种任务。我们不会解释这些任务的细节，我只想说明有各种任务。

• "fine-tune"是指模型被用于预训练，这是网络的BERT部分。该部分的参数是由学习到的BERT的参数来初始化的，以填补空白。
• scratch表示整个模型，包括BERT和Encoder部分都是随机初始化的。

首先，在训练网络时，scratch与用学习填空的BERT初始化的网络相比，损失下降得比较慢，最后，用随机初始化参数的网络的损失仍然高于用学习填空的BERT初始化的参数。

• 当你进行Self-supervised学习时，你使用了大量的无标记数据。
• 另外，Downstream Tasks 需要少量的标记数据。

所谓的 "半监督 "是指，你有大量的无标签数据和少量的有标签数据，这种情况被称为 "半监督"，所以使用BERT的整个过程是连续应用Pre-Train和Fine-Tune，它可以被视为一种半监督方法。

Case 2 ：POS tagging

第二个案例是，输入一个序列，然后输出另一个序列，而输入和输出的长度是一样的。我们在讲Self-Attention的时候，也举了类似的例子。 例如，==POS tagging==。

POS tagging的意思是词性标记。你给机器一个句子，它必须告诉你这个句子中每个词的词性，即使这个词是相同的，也可能有不同的词性。

你只需向BERT输入一个句子。之后，对于这个句子中的每一个标记，它是一个中文单词，有一个代表这个单词的相应向量。然后，这些向量会依次通过Linear transform和Softmax层。最后，网络会预测给定单词所属的类别，例如，它的词性。

当然，类别取决于你的任务，如果你的任务不同，相应的类别也会不同。接下来你要做的事情和案例1完全一样。换句话说，你需要有一些标记的数据。这仍然是一个典型的分类问题。唯一不同的是，BERT部分，即网络的Encoder部分，其参数不是随机初始化的。在预训练过程中，它已经找到了不错的参数。

当然，我们在这里展示的例子属于自然语言处理。但是，你可以把这些例子改成其他任务，例如，你可以把它们改成语音任务，或者改成计算机视觉任务。我在Self-supervised Learning一节中提到，语音、文本和图像都可以表示为一排向量。虽然下面的例子是文字，但这项技术不仅限于处理文字，它还可以用于其他任务，如计算机视觉。

Case 3：Natural Language Inference

在案例3中，模型输入两个句子，输出一个类别。好了，第三个案例以两个句子为输入，输出一个类别，什么样的任务采取这样的输入和输出？ 最常见的是Natural Language Inference ，它的缩写是NLI

机器要做的是判断，是否有可能从前提中推断出假设。这个前提与这个假设相矛盾吗？或者说它们不是相矛盾的句子？

在这个例子中，我们的前提是，一个人骑着马，然后他跳过一架破飞机，这听起来很奇怪。但这个句子实际上是这样的。这是一个基准语料库中的例子。

这里的假设是，这个人在一个餐馆。所以推论说这是一个矛盾。

所以机器要做的是，把两个句子作为输入，并输出这两个句子之间的关系。这种任务很常见。它可以用在哪里呢？例如，舆情分析。给定一篇文章，下面有一个评论，这个消息是同意这篇文章，还是反对这篇文章？该模型想要预测的是每条评论的位置。事实上，有很多应用程序接收两个句子，并输出一个类别。

BERT是如何解决这个问题的？你只要给它两个句子，我们在这两个句子之间放一个特殊的标记，并在最开始放CLS标记。

这个序列是BERT的输入。但我们只把CLS标记作为Linear transform的输入。它决定这两个输入句子的类别。对于NLI，你必须问，这两个句子是否是矛盾的。它是用一些预先训练好的权重来初始化的。

Case 4：Extraction-based Question Answering (QA)

如果你不理解前面的案例，就忘掉它们。这第四个案例，就是我们在作业7中要做的。作业7是一个问题回答系统。也就是说，在机器读完一篇文章后，你问它一个问题，它将给你一个答案。

但是，这里的问题和答案稍有限制。这是Extraction-based的QA。也就是说，我们假设答案必须出现在文章中。答案必须是文章中的一个片段。

在这个任务中，一个输入序列包含一篇文章和一个问题，文章和问题都是一个序列。对于中文来说，每个d代表一个汉字，每个q代表一个汉字。你把d和q放入QA模型中，我们希望它输出两个正整数s和e。根据这两个正整数，我们可以直接从文章中截取一段，它就是答案。这个片段就是正确的答案。

这听起来很疯狂，但是，这是现在使用的一个相当标准的方法。六年前，当我第一次听说这个机制可以解决QA任务时，我简直不敢相信。但是，无论如何，这是今天一个非常普遍的方法。

好吧，如果你仍然不明白我在说什么，更具体地说，这里有一个问题和一篇文章，正确答案是 "gravity"。机器如何输出正确答案？

你的保证模型应该输出，s等于17，e等于17，来表示gravity。因为它是整篇文章中的第17个词，所以s等于17，e等于17，意味着输出第17个词作为答案。或者举另一个例子，答案是，"within a cloud"，这是文章中的第77至79个词。你的模型要做的是，输出77和79这两个正整数，那么文章中从第77个词到第79个词的分割应该是最终的答案。这就是作业7要你做的。当然，我们不是从头开始训练QA模型，为了训练这个QA模型，我们使用BERT预训练的模型。

这个解决方案是这样的。对于BERT来说，你必须向它展示一个问题，一篇文章，以及在问题和文章之间的一个特殊标记，然后我们在开头放一个CLS标记。在这个任务中，你唯一需要从头训练的只有两个向量。"从头训练 "是指随机初始化。这里我们用橙色向量和蓝色向量来表示，这两个向量的长度与BERT的输出相同。假设BERT的输出是768维的向量，这两个向量也是768维的向量。那么，如何使用这两个向量？

首先,计算这个橙色向量和那些与文件相对应的输出向量的内积,由于有3个代表文章的标记,它将输出三个向量,计算这三个向量与橙色向量的内积,你将得到三个值,然后将它们通过softmax函数,你将得到另外三个值。

这个内积和attention很相似，你可以把橙色部分看成是query，黄色部分看成是key，这是一个attention，那么我们应该尝试找到分数最大的位置，就是这里，橙色向量和d2的内积，如果这是最大值，s应该等于2，你输出的起始位置应该是2蓝色部分做的是完全一样的事情。

蓝色部分代表答案的终点，我们计算这个蓝色向量与文章对应的黄色向量的内积，然后，我们在这里也使用softmax，最后，找到最大值，如果第三个值是最大的，e应该是3，正确答案是d2和d3。

因为答案必须在文章中，如果答案不在文章中，你就不能使用这个技巧。这就是一个QA模型需要做的。注意，这两个向量是随机初始化的,而BERT是通过它预先训练的权重初始化的。

Q&A

Q：==BERT的输入长度有限制吗？ ==

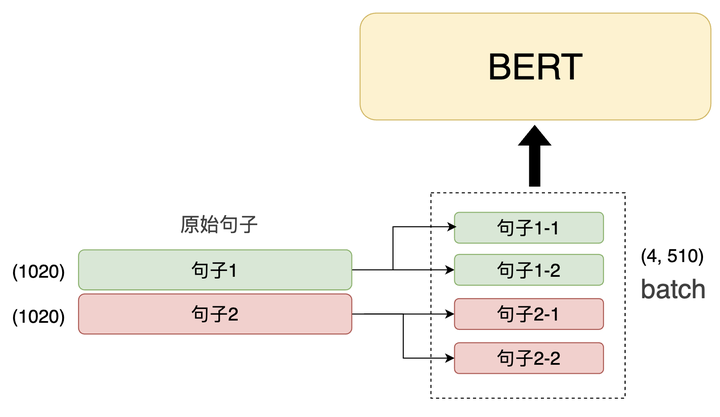
A：理论上，没有。在现实中，是的，在理论上，因为BERT模型，是一个transformer的Encoder，所以它可以输入很长的序列，只要你必须能够做Self-Attention，但Self-Attention的计算复杂性是非常高的。所以你会发现，在实践中，BERT实际上不能输入太长的序列，你最多可以输入512长度的序列，如果你输入一个512长度的序列，Self-Attention在中间就要产生512乘以512大小的Attention Metric，那么你可能会被计算所淹没。所以实际上它的长度不是无限的。在助教的程序中，已经为大家处理了这个问题。我们限制了BERT的输入长度，而且用一篇文章来训练需要很长的时间。然后每次，我们只取其中的一段进行训练。我们不会将整篇文章输入BERT。因为你想要的距离太长了，你的训练会有问题。

Q： "它与填空题有什么关系？

A：",哇，这个问题很好。,你会认为这个填空题只是一个填空题。但我要在这里做一个Q&A。,这两件事之间有什么关系呢？这里先卖个关子，待会会试着回答你。

Training BERT is challenging!

BERT是这样一个著名的模型，它可以做任何事情，那么你可能会认为BERT，在预训练中，它只是填空题，但是，你自己真的不能把它训练起来。

首先，谷歌最早的BERT,它使用的数据规模已经很大了,它的数据中包含了30亿个词汇,30亿个词汇有多少？,是《哈利波特全集》的3000倍。,《哈利波特全集》大约是100万个词汇。,那么谷歌在训练BERT时，最早的BERT，它使用的数据量是《哈利波特全集》的3000倍。

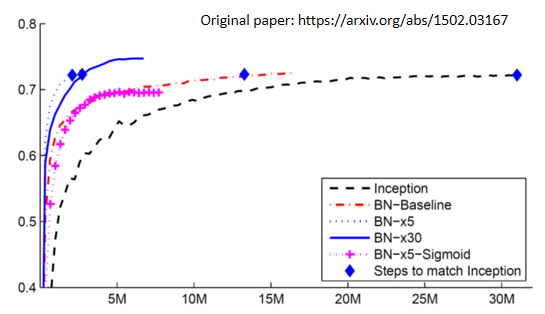
所以你处理起来会比较痛苦,更痛苦的是训练过程,为什么我知道训练过程是痛苦的呢,因为我们实验室有一个学生,他其实是助教之一,他自己试着训练一个BERT,他觉得他不能重现谷歌的结果,好,那么在这个图中,纵轴代表GLUE分数,我们刚才讲到GLUE,对吧?有9个任务，平均有9个任务，,平均分数就叫GLUE分数,好的，那么蓝线就是，谷歌原来的BERT的GLUE分数。

那么我们的目标其实不是实现BERT，我们的目标是实现ALBERT。ALBERT是一个高级版本，是橙色的线，蓝线是我们自己训练的ALBERT，但是我们实际训练的不是最大版本，BERT有一个base版本和一个large版本。对于大版本，我们很难自己训练它，所以我们尝试用最小的版本来训练，看它是否与谷歌的结果相同。

你可能会说这30亿个数据，30亿个词似乎有很多数据。实际上，因为它是无标签数据，所以你只是从互联网上整理了一堆文本，有相同的信息量。所以你要爬上这个级别的信息并不难，难的是训练过程

好的，这个横轴是训练过程，参数更新多少次，大约一百万次的更新，需要多长时间，用TPU运行8天，所以你的TPU要运行8天，如果你在Colab上做，这个至少要运行200天，你甚至可能到明年才能得到结果。

所以，你真的很难自己训练这种BERT模型。幸运的是，作业只是对它进行微调。你可以在Colab上进行微调，在Colab上微调BERT只需要半小时到一小时。但是，如果你想从头开始训练它，也就是说，训练它做填空题，这将需要大量的时间，而且，你不能在Colab上自己完成它。

BERT Embryology (胚胎學)

谷歌已经训练了BERT，而且这些Pre-Train模型是公开的，我们自己训练一个，结果和谷歌的BERT差不多，这有什么意义呢？其实是想建立==BERT胚胎学==。"BERT胚胎学是什么意思？"

我们知道在BERT的训练过程中需要非常大的计算资源，所以我们想知道有没有可能，节省这些计算资源？有没有可能让它训练得更快？,要知道如何让它训练得更快，也许我们可以从观察它的训练过程开始。

过去没有人观察过BERT的训练过程。因为在谷歌的论文中，他们只是告诉你，我有这个BERT。然后它在各种任务中做得很好。

BERT在学习填空的过程中，学到了什么？"它在这个过程中何时学会填动词？什么时候学会填名词？ 什么时候学会填代词？ 没有人研究过这个问题。

所以我们自己训练BERT后，可以观察到BERT什么时候学会填什么词汇，它是如何提高填空能力的？ 好了，细节不是这门课的重点，所以我不在这里讲了。我把论文的链接https://arxiv.org/abs/2010.02480放在这里，供大家参考。不过可以提前爆冷一下就是：事实和你直观想象的不一样。

Pre-training a seq2seq model

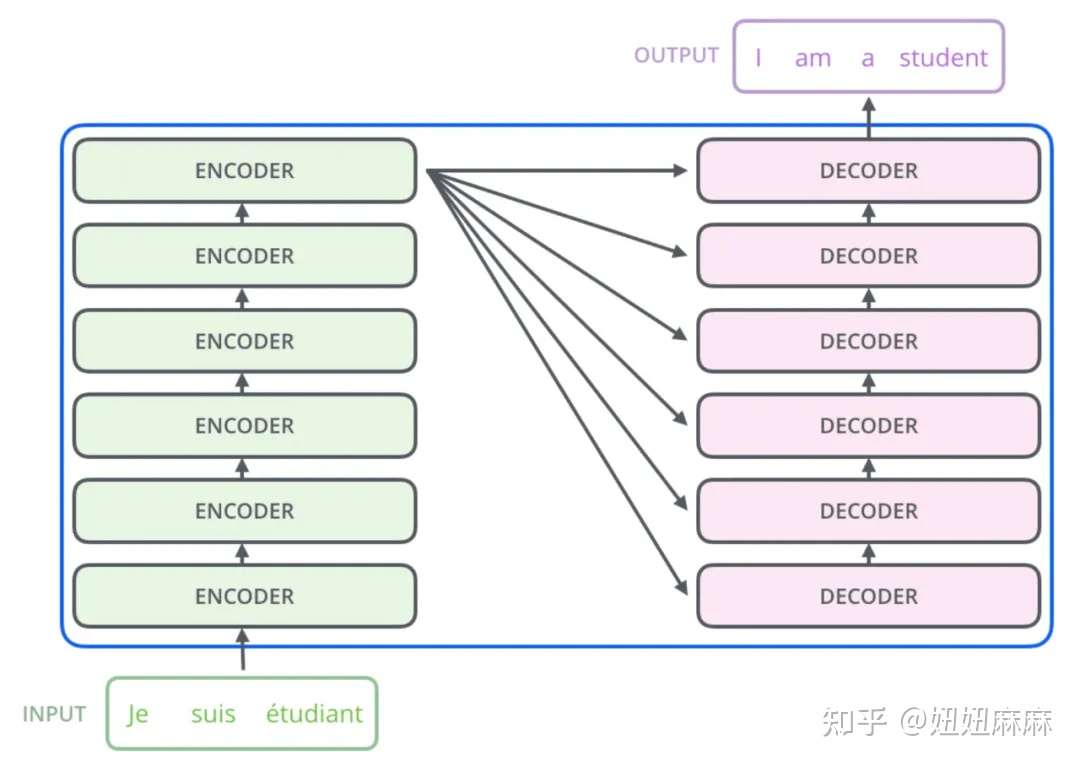
我们补充一点，上述的任务都不包括，Seq2Seq模型，如果我们要解决，Seq2Seq模型呢？BERT只是一个预训练Encoder，有没有办法预训练Seq2Seq模型的Decoder？

有，你就说我有一个Seq2Seq模型，有一个transformer，还有一个Encoder和Decoder。输入是一串句子，输出是一串句子，中间用Cross Attention连接起来，然后你故意在Encoder的输入上做一些干扰来破坏它，我以后会具体告诉你我说的 "破坏 "是什么意思

Encoder看到的是被破坏的结果，那么Decoder应该输出句子被破坏前的结果，训练这个模型实际上是预训练一个Seq2Seq模型。

有一篇论文叫MASS：

在MASS中，它说破坏的方法是，就像BERT做的那样，只要遮住一些地方就可以了，然后有各种方法来破坏它，比如，删除一些词，打乱词的顺序，旋转词的顺序。或者插入一个MASK，再去掉一些词。总之，有各种方法。在破坏了输入的句子之后，它可以通过Seq2Seq模型来恢复它。

你可能会问,有那么多的mask方法,哪种方法更好呢?也许你想自己做一些实验来试试,让我告诉你,你不需要做,谷歌为你做的,有一篇论文叫T5。

T5的全称是Transfer Text-To-Text Transformer，有五个T，所以叫T5。在这个T5里面，它只是做了各种尝试，它做了你能想象的所有组合。这篇论文有67页，你可以回去读一下，看看结论。

T5是在一个语料库上训练的，叫 "Colossal Clean Crawled Corpus"，对于这个数据集，Colossal就是巨无霸，就是非常巨大的意思，它叫C4，你用C4来训练T5，大家都是命名高手。这个命名非常强大，这个C4有多大？

C4是一个公共数据集，你可以下载它，它是公共的，但是它的原始文件大小是7TB，你可以下载它，但是你不知道把它保存在哪里，加载之后，你可以通过脚本做预处理，由谷歌提供。这个脚本有一个文件，我看到它在网站上发布了，语料库网站上的文件说，用一个GPU做预处理需要355天，你可以下载它，但你在预处理时有问题。所以，你可以发现，在深度学习中，数据量和模型都很惊人。

Fun Facts about BERT

Why does BERT work?

"为什么BERT有用？"最常见的解释是，当输入一串文本时，每个文本都有一个对应的向量。对于这个向量，我们称之为embedding。

它的特别之处在于，这些向量代表了输入词的含义。例如，模型输入 "台湾大学"（国立台湾大学），输出4个向量。这4个向量分别代表 "台"、"湾"、"大 "和 "学"。更具体地说，如果你把这些词所对应的向量画出来，或者计算它们之间的距离。

你会发现，意思比较相似的词，它们的向量比较接近。例如，水果和草都是植物，它们的向量比较接近。但这是一个假的例子，我以后会给你看一个真正的例子。"鸟 "和 "鱼 "是动物，所以它们可能更接近。

你可能会问，中文有歧义，其实不仅是中文，很多语言都有歧义，BERT可以考虑上下文，所以，同一个词，比如说 "苹果"，它的上下文和另一个 "苹果 "不同，它们的向量也不会相同。

水果 "苹果 "和手机 "苹果 "都是 "苹果"，但根据上下文，它们的含义是不同的。所以，它的向量和相应的embedding会有很大不同。水果 "苹果 "可能更接近于 "草"，手机 "苹果 "可能更接近于 "电"。

现在我们看一个真实的例子。假设我们现在考虑 "苹果 "这个词，我们会收集很多有 "苹果 "这个词的句子，比如 "喝苹果汁"、"苹果Macbook "等等。然后，我们把这些句子放入BERT中。

接下来，我们将计算 "苹果 "一词的相应embedding。输入 "喝苹果汁"，得到一个 "苹果 "的向量。为什么不一样呢？在Encoder中存在Self-Attention，所以根据 "苹果 "一词的不同语境，得到的向量会有所不同。接下来，我们计算这些结果之间的==cosine similarity==，即计算它们的相似度。结果是这样的，这里有10个句子：

• 前5个句子中的 "苹果 "代表可食用的苹果。例如，第一句是 "我今天买了苹果吃"，第二句是 "进口富士苹果平均每公斤多少钱"，第三句是 "苹果茶很难喝"，第四句是 "智利苹果的季节来了"，第五句是 "关于进口苹果的事情"，这五个句子都有 "苹果 "一词，

• 后面五个句子也有 "苹果 "一词，但提到的是苹果公司的苹果。例如，"苹果即将在下个月发布新款iPhone"，"苹果获得新专利"，"我今天买了一部苹果手机"，"苹果股价下跌"，"苹果押注指纹识别技术"，共有十个 "苹果"

计算每一对之间的相似度，得到一个10×10的矩阵。相似度越高，这个颜色就越浅。所以，自己和自己之间的相似度一定是最大的，自己和别人之间的相似度一定是更小的。但前五个 "苹果 "和后五个 "苹果 "之间的相似度相对较低。 BERT知道，前五个 "苹果 "是指可食用的苹果，所以它们比较接近。最后五个 "苹果 "指的是苹果公司，所以它们比较接近。所以BERT知道，上下两堆 "苹果 "的含义不同。

BERT的这些向量是输出向量，每个向量代表该词的含义。BERT在填空的过程中已经学会了每个汉字的意思。",也许它真的理解了中文，对它来说，汉字不再是毫无关联的，既然它理解了中文，它就可以在接下来的任务中做得更好。

那么接下来你可能会问，"为什么BERT有如此神奇的能力？",为什么......,为什么它能输出代表输入词含义的向量？ 这里，约翰-鲁伯特-弗斯，一位60年代的语言学家，提出了一个假说。他说，要知道一个词的意思，我们需要看它的 "Company"，也就是经常和它一起出现的词汇，也就是它的上下文。

一个词的意思，取决于它的上下文

• 所以以苹果（apple）中的果字为例。如果它经常与 "吃"、"树 "等一起出现，那么它可能指的是可食用的苹果。

• 如果它经常与电子、专利、股票价格等一起出现，那么它可能指的是苹果公司。

当我们训练BERT时，我们给它w1、w2、w3和w4，我们覆盖w2，并告诉它预测w2，而它就是从上下文中提取信息来预测w2。所以这个向量是其上下文信息的精华，可以用来预测w2是什么。

这样的想法在BERT之前已经存在了。在word embedding中，有一种技术叫做CBOW。

CBOW所做的，与BERT完全一样。做一个空白，并要求它预测空白处的内容。这个CBOW，这个word embedding技术，可以给每个词汇一个向量，代表这个词汇的意义。

CBOW是一个非常简单的模型，它使用两个变换，是一个非常简单的模型，有人会问，"为什么它只使用两个变换？"，"它可以更复杂吗？"，CBOW的作者，Thomas Mikolov，曾经来到台湾。当时我在上课的时候，经常有人问我，为什么CBOW只用线性，为什么不用深度学习，我问过Thomas Mikolov这个问题，他说可以用深度学习，但是之所以选择线性模型，一个简单的模型，最大的担心，其实是算力问题。当时的计算能力和现在不在一个数量级上，可能是2016年的时候，几年前的技术也不在一个数量级上，当时要训练一个非常大的模型还是比较困难的，所以他选择了一个比较简单的模型。

今天，当你使用BERT的时候，就相当于一个深度版本的CBOW。你可以做更复杂的事情，而且BERT还可以根据不同的语境，从同一个词汇产生不同的embedding。因为它是一个考虑到语境的高级版本的词embedding，BERT也被称为Contextualized embedding，这些由BERT提取的向量或embedding被称为Contextualized embedding，希望大家能接受这个答案。

但是，这个答案，它真的是真的吗？

这是你在文献中听到最多的答案。当你和别人讨论BERT时，这是大多数人都会告诉你的理由。它真的是真的吗？这里有一个难以理解的，由我们实验室的一个学生做的实验。实验是这样的：我们应用为文本训练的BERT对蛋白质、DNA链和音乐进行分类。

让我们以DNA链的分类为例。DNA是一系列的脱氧核团核酸，有四种，分别用A、T、C和G表示，所以一条DNA链是这样的。你可能会问，"EI IE和N代表什么？"不要在意细节，我也不知道，总之，这是一个分类问题。只要用训练数据和标记数据来训练它，就可以了。神奇的部分来了，DNA可以用ATCG来表示，现在，我们要用BERT来对DNA进行分类：

例如，"A "是 "we"，"T "是 "you"，"C "是 "he"，"G "是 "she"。对应的词并不重要，你可以随机生成。"A "可以对应任何词汇，"T"、"C "和 "G "也可以，这并不重要，对结果影响很小。只是这串文字无法理解。

例如，"AGAC "变成了 "we she we he"，不知道它在说什么。然后，把它扔进一个一般的BERT，用CLS标记，一个输出向量，一个Linear transform，对它进行分类。只是分类到了DNA类,我不知道他们是什么意思。和以前一样，Linear transform使用随机初始化，而BERT是通过预训练模型初始化的。但用于初始化的模型，是学习填空的模型。它已经学会了英语填空。你可能会认为,这个实验完全是无稽之谈。如果我们把一个DNA序列预处理成一个无意义的序列,那么BERT的目的是什么? 大家都知道,BERT可以分析一个有效句子的语义,你怎么能给它一个无法理解的句子呢? 做这个实验的意义是什么?

蛋白质有三种分类，那么蛋白质是由氨基酸组成的，有十种氨基酸，只要给每个氨基酸一个随机的词汇，那么DNA是一组ATCG，音乐也是一组音符，给它每个音符一个词汇，然后，把它作为一个文章分类问题来做。

你会发现，如果你不使用BERT，你得到的结果是蓝色部分，如果你使用BERT，你得到的结果是红色部分，这实际上更好，你们大多数人现在一定很困惑。这个实验只能用神奇来形容，没有人知道它为什么有效，而且目前还没有很好的解释，我之所以要谈这个实验，是想告诉你们，要了解BERT的力量，还有很多工作要做。

我并不是要否认BERT能够分析句子的含义这一事实。从embedding中，我们清楚地观察到，BERT知道每个词的含义，它能找出含义相似的词和不相似的词。但正如我想指出的那样，即使你给它一个无意义的句子，它仍然可以很好地对句子进行分类。

所以，也许它的力量并不完全来自于对实际文章的理解。也许还有其他原因。例如，也许，BERT只是一套更好的初始参数。也许这与语义不一定有关。也许这套初始参数，只是在训练大型模型时更好。

是这样吗？这个问题需要进一步研究来回答。我之所以要讲这个实验，是想让大家知道，我们目前使用的模型往往是非常新的，需要进一步的研究，以便我们了解它的能力。如果你想了解更多关于BERT的知识，你可以参考这些链接。你的作业不需要它，,这学期剩下的时间也不需要。我只想告诉你，BERT还有很多其他的变种。

Multi-lingual BERT

接下来，我要讲的是，一种叫做Multi-lingual BERT的BERT（多语言）。Multi-lingual BERT有什么神奇之处？

它是由很多语言来训练的，比如中文、英文、德文、法文等等，用填空题来训练BERT，这就是Multi-lingual BERT的训练方式。

Zero-shot Reading Comprehension

google训练了一个Multi-lingual BERT，它能够做这104种语言的填空题。神奇的地方来了，如果你用英文问答数据训练它，它就会自动学习如何做中文问答：

我不知道你是否完全理解我的意思，所以这里有一个真实的实验例子。

这是一些训练数据。他们用SQuAD进行fine-tune。这是一个英文Q&A数据集。中文数据集是由台达电发布的，叫DRCD。这个数据集也是我们在作业中要用到的数据集。

在BERT提出之前，效果并不好。在BERT之前，最强的模型是QANet。它的正确率只有......，嗯，我是说F1得分，而不是准确率，但你可以暂时把它看成是准确率或正确率。

如果我们允许用中文填空题进行预训练，然后用中文Q&A数据进行微调，那么它在中文Q&A测试集上的正确率达到89%。因此，其表现是相当令人印象深刻的。

神奇的是，如果我们把一个Multi-lingual的BERT，用英文Q&A数据进行微调，它仍然可以回答中文Q&A问题，并且有78%的正确率，这几乎与QANet的准确性相同。它从未接受过中文和英文之间的翻译训练，也从未阅读过中文Q&A的数据收集。,它在没有任何准备的情况下参加了这个中文Q&A测试，尽管它从未见过中文测试，但不知为何，它能回答这些问题。

Cross-lingual Alignment?

你们中的一些人可能会说："它在预训练中读过104种语言，104种语言中的一种是中文，是吗？ 如果是，这并不奇怪。"但是在预训练中，学习的目标是填空。它只能用中文填空。有了这些知识，再加上做英文问答的能力，不知不觉中，它就自动学会了做中文问答。

听起来很神奇，那么BERT是怎么做到的呢？一个简单的解释是：也许对于多语言的BERT来说，不同的语言并没有那么大的差异。无论你用中文还是英文显示，对于具有相同含义的单词，它们的embedding都很接近。

汉语中的 "跳 "与英语中的 "jump "接近，汉语中的 "鱼 "与英语中的 "fish "接近，汉语中的 "游 "与英语中的 "swim "接近，也许在学习过程中它已经自动学会了。它是可以被验证的。我们实际上做了一些验证。验证的标准被称为Mean Reciprocal Rank，缩写为MRR。我们在这里不做详细说明。你只需要知道，MRR的值越高，不同embedding之间的Alignment就越好。

更好的Alignment意味着，具有相同含义但来自不同语言的词将被转化为更接近的向量。如果MRR高，那么具有相同含义但来自不同语言的词的向量就更接近。

这条深蓝色的线是谷歌发布的104种语言的Multi-lingual BERT的MRR，它的值非常高，这说明不同语言之间没有太大的差别。Multi-lingual BERT只看意思，不同语言对它没有太大的差别。

橙色这条是我们试图自己训练Multi-lingual BERT。我们使用的数据较少，每种语言只使用了20万个句子。数据较少。我们自我训练的模型结果并不好。我们不知道为什么我们的Multi-lingual BERT不能将不同的语言统一起来。似乎它不能学习那些在不同语言中具有相同含义的符号，它们应该具有相同的含义。这个问题困扰了我们很长时间。

为什么我们要做这个实验？为什么我们要自己训练Multi-lingual BERT？因为我们想了解，是什么让Multi-lingual BERT。我们想设置不同的参数，不同的向量，看看哪个向量会影响Multi-lingual BERT。

但是我们发现，对于我们的Multi-lingual BERT来说，无论你如何调整参数，它就是不能达到Multi-lingual的效果，它就是不能达到Alignment的效果。我们把数据量增加了五倍，看看能不能达到Alignment的效果。在做这个实验之前，大家都有点抵触，大家都觉得有点害怕，因为训练时间要比原来的长五倍。训练了两天后，什么也没发生，损失甚至不能减少，就在我们要放弃的时候，损失突然下降了。

用了8个V100来训练，我们的实验室也没有8个V100，是在NCHC（国家高性能计算中心）的机器上运行的，训练了两天后，损失没有下降，似乎失败了。当我们要放弃的时候，损失下降了。

这是某个学生在Facebook上发的帖子，我在这里引用它来告诉你，我当时心里的感叹。整个实验，必须运行一个多星期，才能把它学好，每一种语言1000K的数据。

所以看起来，数据量是一个非常关键的因素，关系到能否成功地将不同的语言排列在一起。所以有时候，神奇的是，很多问题或很多现象，只有在有足够的数据量时才会显现出来。它可以在A语言的QA上进行训练，然后直接转移到B语言上，从来没有人说过这一点。这是过去几年才出现的，一个可能的原因是，过去没有足够的数据，现在有足够的数据，现在有大量的计算资源，所以这个现象现在有可能被观察到。

最后一个神奇的实验，我觉得这件事很奇怪：

Why？

你说BERT可以把不同语言中含义相同的符号放在一起，使它们的向量接近。但是，当训练多语言的BERT时，如果给它英语，它可以用英语填空，如果给它中文，它可以用中文填空，它不会混在一起。那么，如果不同语言之间没有区别，怎么可能只用英语标记来填英语句子呢？为什么它不会用中文符号填空呢？它就是不填，这说明它知道语言的信息也是不同的，那些不同语言的符号毕竟还是不同的，它并没有完全抹去语言信息，所以我想出了一个研究课题，我们来找找，语言信息在哪里。

后来我们发现，语言信息并没有隐藏得很深。一个学生发现，我们把所有英语单词的embedding，放到多语言的BERT中，取embedding的平均值，我们对中文单词也做同样的事情。在这里，我们给Multi-lingual BERT一个英语句子，并得到它的embedding。我们在embedding中加上这个蓝色的向量，这就是英语和汉语之间的差距。

这些向量，从Multi-lingual BERT的角度来看，变成了汉语。有了这个神奇的东西，你可以做一个奇妙的无监督翻译。例如，你给BERT看这个中文句子。

这个中文句子是，"能帮助我的小女孩在小镇的另一边，，没人能够帮助我"，现在我们把这个句子扔到Multi-lingual BERT中。然后我们取出Multi-lingual BERT中的一个层，它不需要是最后一层，可以是任何一层。我们拿出某一层，给它一个embedding，加上这个蓝色的向量。对它来说，这个句子马上就从中文变成了英文。

在向BERT输入英文后，通过在中间加一个蓝色的向量来转换隐藏层，转眼间，中文就出来了。"没有人可以帮助我"，变成了 "是（是）没有人（没有人）可以帮助我（我）"，"我 "变成了 "我"，"没有人 "变成了 "没有人"，所以它在某种程度上可以做无监督的标记级翻译，尽管它并不完美，神奇的是，Multi-lingual的BERT仍然保留了语义信息。

BERT Q&A

1.1 Bert 如何解决长文本问题？ -

何枝的回答 - 知乎 https://www.zhihu.com/question/327450789/answer/2455518614

当我们遇到一个文本分类问题，大多数人首先会想到用BERT系列的模型做尝试。对于短文本而言（小于等于510个token）是work的，但如果遇到输入文本大于510个token时，此时就无法直接调用开源的pretrained-model来做fine-tuning了，本篇文章将通过Pooling的方法来尝试解决长文本下的分类问题。

要想将一个大于510个token的文本输入，一般有以下几种方法：

• Clipping（截断法）：对长输入进行截断，挑选其中「重要」的token输入模型。一种最常见的办法是挑选文章的前 Top N 个 token，和文末的 Top K 个 token，保证 N + K <= 510，这种方法基于的前提假设是「文章的首尾信息最能代表篇章的全局概要」；此外，还有一种 two stage 的方法：先将文章过一遍 summarize 的模型，再将 summarize 模型的输出喂给分类模型。但无论哪种截断方式，都必将会丢失一部分的文本信息，可能会导致分类错误。
• Pooling（池化法）：截断法最大的问题在于需要丢掉一部分文本信息，如果我们能够保留文本中的所有信息，想办法让模型能够接收文本中的全部信息，这样就能避免文本丢失带来的影响。
• RNN（循环法）：BERT之所以会有最大长度的限制，是因为其在进行MLM预训练的时候就规定了最大的输入长度，而对于类RNN的网络来讲则不会有句子长度的限制（有多少个token就过多少次NN就行了）。但RNN相较于 Transformer 来讲最大问题就在于效果不好，如何将 RNN 的思想用在 Transformer 中就是一个比较有意思的话题了。推荐可以看看ERNIE-DOC，官网上是这么描述的，感兴趣的同学可以研究研究

#### Pooling思想

#### 1.1 句子分片

由于 BERT 最多只能接受 510 个token 的输入，因此我们需要将长文本切割成若干段。

假设我们有 2 句 1000 个 token 的句子，那么我就需要先将这 2 个句子切成 4 段（第 1 个句子的 2 段 + 第 2 个句子的 2 段），并放到一个 batch 的输入中喂给模型。

文本分段，BERT输入数据维度（4, 510）

#### 1.2 Pooling

当切完片后的数据喂给 BERT 后，我们取 BERT 模型的 [CLS] 的输出，此时输出维度应该为：(4, 768) 。

随即，我们需要将这 4 个 output 按照所属句子分组，由下图所示，前 2 个向量属于一个句子，因此我们将它们归为一组，此时的维度变化：(4, 768) -> (2, 2, 768)。

接着，我们对同一组的向量进行 Pooling 操作，使其下采样为 1 维的向量，即（1, 768）。

Pooling 的方式有两种：Max-Pooling 和 Avg-Pooling，我们会在后面的实验中比较两种不同 Pooling 的效果。

这里推荐大家使用Max-Pooling比较好，因为 Avg-Pooling 很有可能把特征值给拉平，选择保留显著特征（Max-Pooling）效果会更好一些。

一、李宏毅 - Transformer_Encoder

变形金刚的英文就是Transformer,那Transformer也跟我们之后会,提到的BERT有非常强烈的关系,所以这边有一个BERT探出头来,代表说Transformer跟BERT,是很有关系的。

1.1 Sequence-to-sequence (Seq2seq)

Transformer就是一个,==Sequence-to-sequence==的model,他的缩写,我们会写做==Seq2seq==,那Sequence-to-sequence的model,又是什么呢？

举例来说,Seq2seq一个很好的应用就是 语音辨识：

在做语音辨识的时候,输入是声音讯号,声音讯号其实就是一串的vector,输出是语音辨识的结果,也就是输出的这段声音讯号,所对应的文字。我们这边用圈圈来代表文字,每一个圈圈就代表,比如说中文里面的一个方块子,今天输入跟输出的长度,当然是有一些关系,但是却没有绝对的关系，输入的声音讯号,他的长度是大T,我们并没有办法知道说,根据大T输出的这个长度N一定是多少。输出的长度由机器自己决定,由机器自己去听这段声音讯号的内容,自己决定他应该要输出几个文字,他输出的语音辨识结果,输出的句子里面应该包含几个字,由机器自己来决定,这个是语音辨识。

1.2 Question Answering (QA)

那事实上Seq2Seq model,在NLP的领域,在natural language processing的领域的使用,是比你想像的更为广泛,其实很多natural language processing的任务,都可以想成是==question answering,QA==的任务。Question Answering,就是给机器读一段文字,然后你问机器一个问题,希望他可以给你一个正确的答案。

• 假设你今天想做的是翻译,那机器读的文章就是一个英文句子,问题就是这个句子的德文翻译是什么,然后输出的答案就是德文
• 或者是你想要叫机器自动作摘要,摘要就是给机器读一篇长的文章,叫他把长的文章的重点节录出来,那你就是给机器一段文字,问题是这段文字的摘要是什么,然后期待他答案可以输出一个摘要
• 或者是你想要叫机器做Sentiment analysis,Sentiment analysis就是机器要自动判断一个句子,是正面的还是负面的；假设你有做了一个产品,然后上线以后,你想要知道网友的评价,但是你又不可能一直找人家ptt上面,把每一篇文章都读过,所以就做一个Sentiment analysis model,看到有一篇文章里面,有提到你的产品,然后就把这篇文章丢到,你的model里面,去判断这篇文章,是正面还是负面。你就给机器要判断正面还负面的文章,问题就是这个句子,是正面还是负面的,然后希望机器可以告诉你答案

必须要强调一下,对多数NLP的任务,或对多数的语音相关的任务而言,往往为这些任务客制化模型,你会得到更好的结果。但是各个任务客制化的模型,就不是我们这一门课的重点了,如果你对人类语言处理,包括语音 包括自然语言处理,这些相关的任务有兴趣的话呢,可以参考一下以下课程网页的连结,就是去年上的深度学习,与人类语言处理,这门课的内容里面就会教你,各式各样的任务最好的模型,应该是什么。

举例来说在做语音辨识,我们刚才讲的是一个Seq2Seq model,输入一段声音讯号,直接输出文字,今天啊 Google的 pixel4,Google官方告诉你说,Google pixel4也是用,N to N的Neural network,pixel4里面就是,有一个Neural network,输入声音讯号,输出就直接是文字。

但他其实用的不是Seq2Seq model,他用的是一个叫做,RNN transducer的 model,像这些模型他就是为了,语音的某些特性所设计,这样其实可以表现得更好,至于每一个任务,有什么样客制化的模型,这个就是另外一门课的主题,就不是我们今天想要探讨的重点。

1.3 Seq2seq for Syntactic Parsing

在语音还有自然语言处理上的应用,其实有很多应用,你不觉得他是一个Seq2Seq model的问题,但你都可以硬用Seq2Seq model的问题硬解他。

举例来说文法剖析,给机器一段文字,比如Deep learning is very powerful

机器要做的事情是产生,一个文法的剖析树 告诉我们,deep加learning合起来,是一个名词片语,very加powerful合起来,是一个形容词片语,形容词片语加is以后会变成,一个动词片语,动词片语加名词片语合起来,是一个句子。

那今天文法剖析要做的事情,就是产生这样子的一个Syntactic tree,所以在文法剖析的任务里面,假设你想要deep learning解的话,输入是一段文字,他是一个Sequence,但输出看起来不像是一个Sequence,输出是一个树状的结构,但事实上一个树状的结构,可以硬是把他看作是一个Sequence。

这个树状结构可以对应到一个,这样子的Sequence,从这个Sequence里面,你也可以看出

• 这个树状的结构有一个S，有一个左括号,有一个右括号
• S里面有一个noun phrase,有一个左括号跟右括号
• NP里面有一个左括号跟右括号,NP里面有is
• 然后有这个形容词片语,他有一个左括号右括号

这一个Sequence就代表了这一个tree 的structure,你先把tree 的structure,转成一个Sequence以后,你就可以用Seq2Seq model硬解他。train一个Seq2Seq model,读这个句子,然后直接输入这一串文字,再把这串文字转成一个树状的结构,你就可以硬是用Seq2Seq model,来做文法剖析这件事,这个概念听起来非常的狂,但这是真的可以做得到的。

1.4 multi-label classification

还有一些任务可以用seq2seq's model,举例来说 ==multi-label的classification==。==multi-class==的classification,跟==multi-label==的classification,听起来名字很像,但他们其实是不一样的事情,multi-class的classification意思是说,我们有不只一个class机器要做的事情,是从数个class里面,选择某一个class出来。

但是multi-label的classification,意思是说同一个东西,它可以属于多个class,举例来说 你在做文章分类的时候。

可能这篇文章 属于class 1跟3,这篇文章属于class 3 9 17等等,你可能会说,这种multi-label classification的问题,能不能直接把它当作一个multi-class classification的问题来解

举例来说,我把这些文章丢到一个classifier里面：

• 本来classifier只会输出一个答案,输出分数最高的那个答案
• 我现在就输出分数最高的前三名,看看能不能解,multi-label的classification的问题

但这种方法可能是行不通的,因为每一篇文章对应的class的数目,根本不一样 有些东西 有些文章,对应的class的数目,是两个 有的是一个 有的是三个。所以 如果你说 我直接取一个threshold,我直接取分数最高的前三名,class file output分数最高的前三名,来当作我的输出 显然,不一定能够得到好的结果 那怎么办呢？

这边可以用seq2seq硬做,输入一篇文章 输出就是class 就结束了,机器自己决定 它要输出几个class。我们说seq2seq model,就是由机器自己决定输出几个东西,输出的output sequence的长度是多少,既然你没有办法决定class的数目,那就让机器帮你决定,每篇文章 要属于多少个class。

1.5 Encoder-Decoder

我们现在就是要来学,怎么做seq2seq这件事,一般的seq2seq's model,它里面会分成两块一块是Encoder,另外一块是Decoder。

你input一个sequence有Encoder,负责处理这个sequence,再把处理好的结果丢给Decoder,由Decoder决定,它要输出什么样的sequence,等一下 我们都还会再细讲,Encoder跟 Decoder内部的架构。seq2seq model的起源,其实非常的早 在14年的9月,就有一篇seq2seq's model,用在翻译的文章 被放到Arxiv上。

可以想像当时的seq2seq's model,看起来还是比较年轻的,今天讲到seq2seq's model的时候,大家第一个会浮现在脑中的,可能都是我们今天的主角,也就是transformer。

它有一个Encoder架构,有一个Decoder架构,它里面有很多花花绿绿的block,等一下就会讲一下,这里面每一个花花绿绿的block,分别在做的事情是什么。

1.5.1 Encoder

seq2seq model ==Encoder==要做的事情,就是给一排向量，输出另外一排向量

给一排向量、输出一排向量这件事情,很多模型都可以做到,可能第一个想到的是,我们刚刚讲完的self-attention,其实不只self-attention,RNN CNN 其实也都能够做到,input一排向量, output另外一个同样长度的向量。

在transformer里面,transformer的Encoder,用的就是self-attention, 这边看起来有点复杂,我们用另外一张图,来仔细地解释一下,这个Encoder的架构,等一下再来跟原始的transformer的,论文里面的图进行比对。

现在的Encoder里面,会分成很多很多的block：

每一个block都是输入一排向量,输出一排向量,你输入一排向量 第一个block,第一个block输出另外一排向量,再输给另外一个block,到最后一个block,会输出最终的vector sequence,每一个block 其实,并不是neural network的一层。

每一个block里面做的事情,是好几个layer在做的事情,在transformer的Encoder里面,每一个block做的事情,大概是这样子的：

• 先做一个self-attention,input一排vector以后,做self-attention,考虑整个sequence的资讯，Output另外一排vector。
• 接下来这一排vector,会再丢到fully connected的feed forward network里面,再output另外一排vector,这一排vector就是block的输出。

Multi-self-attention + residual connection

事实上在原来的transformer里面,它做的事情是更复杂的。在之前self-attention的时候,我们说 输入一排vector,就输出一排vector,这边的每一个vector,它是考虑了所有的input以后,所得到的结果：

在transformer里面,它加入了一个设计,我们不只是输出这个vector,我们还要把这个vector加上它的input,它要把input拉过来 直接加给输出,得到新的output。也就是说,这边假设这个vector叫做\(a\),这个vector叫做\(b\) 你要把\(a+b\)当作是新的输出。

这样子的network架构,叫做==residual connection==,那其实这种residual connection,在deep learning的领域用的是非常的广泛,之后如果我们有时间的话,再来详细介绍,为什么要用residual connection。

那你现在就先知道说,有一种network设计的架构,叫做residual connection,它会把input直接跟output加起来,得到新的vector。

Norm

得到residual的结果以后,再把它做一件事情叫做normalization,这边用的不是batch normalization,这边用的叫做==layer normalization==。

layer normalization做的事情,比bacth normalization更简单一点。输入一个向量，输出另外一个向量,不需要考虑batch,它会把输入的这个向量,计算它的mean跟standard deviation。

但是要注意一下,==batch normalization==是对不同example,不同feature的同一个dimension,去计算mean跟standard deviation。但==layer normalization==,它是对同一个feature,同一个example里面,不同的dimension,去计算mean跟standard deviation

计算出mean,跟standard deviation以后,就可以做一个normalize,我们把input 这个vector里面每一个,dimension减掉mean,再除以standard deviation以后得到x',就是layer normalization的输出。 \[ x'_i=\frac{x_i-m}{\sigma} \] 得到layer normalization的输出以后,它的这个输出，才是FC network的输入。

而FC network这边,也有residual的架构,所以 我们会把FC network的input,跟它的output加起来做一下residual,得到新的输出。这个FC network做完residual以后,还不是结束 你要把residual的结果,再做一次layer normalization,得到的输出,才是residual network里面,一个block的输出。

• 首先有self-attention,其实在input的地方,还有加上positional encoding,我们之前已经有讲过,如果你只光用self-attention,你没有未知的资讯,所以你需要加上positional的information,然后在这个图上,有特别画出positional的information。
• Multi-Head Attention,这个就是self-attention的block,这边有特别强调说,它是Multi-Head的self-attention。
• Add&norm,就是residual加layer normalization,我们刚才有说self-attention,有加上residual的connection,加下来还要过layer normalization,这边这个图上的Add&norm,就是residual加layer norm的意思。
• 接下来,要过feed forward network，fc的feed forward network以后再做一次Add&norm,再做一次residual加layer norm,才是一个block的输出。

然后这个block会重复n次,这个复杂的block,其实在之后会讲到的,一个非常重要的模型BERT里面,会再用到 BERT,它其实就是transformer的encoder。

To Learn more

讲到这边 你心里一定充满了问号,就是为什么 transformer的encoder,要这样设计 不这样设计行不行?

行 不一定要这样设计,这个encoder的network架构,现在设计的方式,本文是按照原始的论文讲给你听的,但原始论文的设计 不代表它是最好的,最optimal的设计。

• 有一篇文章叫,on layer normalization in the transformer architecture，它问的问题就是为什么,layer normalization是放在那个地方呢,为什么我们是先做,residual再做layer normalization,能不能够把layer normalization,放到每一个block的input,也就是说 你做residual以后,再做layer normalization,再加进去 你可以看到说左边这个图,是原始的transformer,右边这个图是稍微把block,更换一下顺序以后的transformer,更换一下顺序以后 结果是会比较好的,这就代表说,原始的transformer 的架构,并不是一个最optimal的设计,你永远可以思考看看,有没有更好的设计方式
• 再来还有一个问题就是,为什么是layer norm 为什么是别的,不是别的,为什么不做batch normalization,也许这篇paper可以回答你的问题,这篇paper是Power Norm：,Rethinking Batch Normalization In Transformers,它首先告诉你说 为什么,batch normalization不如,layer normalization,在Transformers里面为什么,batch normalization不如,layer normalization,接下来在说,它提出来一个power normalization,一听就是很power的意思,都可以比layer normalization,还要performance差不多或甚至好一点。

二、李宏毅 - Transformer_decoder P2

2.1 Decoder – Autoregressive (AT)

Decoder其实有两种,接下来会花比较多时间介绍,比较常见的 ==Autoregressive Decoder（自回归解码器）==,这个 Autoregressive 的 Decoder,是怎么运作的。

用语音辨识,来当作例子来说明,或用在作业里面的机器翻译,其实是一模一样的,你只是把输入输出,改成不同的东西而已。语音辨识就是输入一段声音,输出一串文字,你会把一段声音输入给 Encoder,比如说你对机器说,机器学习,机器收到一段声音讯号,声音讯号 进入 Encoder以后,输出会是什么,输出会变成一排 Vector。

Encoder 做的事情,就是输入一个 Vector Sequence,输出另外一个 Vector Sequence。接下来,就轮到 Decoder 运作了,Decoder 要做的事情就是产生输出,也就是产生语音辨识的结果,

Decoder 怎么产生这个语音辨识的结果？

Decoder 做的事情,就是把 Encoder 的输出先读进去,至于怎么读进去,这个我们等一下再讲 我们先,你先假设 Somehow 就是有某种方法,把 Encoder 的输出读到 Decoder 里面,这步我们等一下再处理。

Decoder 怎么产生一段文字？

首先,你要先给它一个特殊的符号,这个特殊的符号,代表开始,在助教的投影片里面,是写 Begin Of Sentence,缩写是 BOS。

BOS就是 Begin 的意思,这个是一个 Special 的 Token,你就是在你的个 Lexicon 里面,你就在你可能,本来 Decoder 可能产生的文字里面,多加一个特殊的字,这个字就代表了 BEGIN,代表了开始这个事情。

在这个机器学习里面,假设你要处理 NLP 的问题,每一个 Token,你都可以把它用一个 One-Hot 的 Vector 来表示,One-Hot Vector 就其中一维是 1,其他都是 0,所以 BEGIN 也是用 One-Hot Vector 来表示,其中一维是 1,其他是 0。 接下来Decoder 会吐出一个向量,这个 Vector 的长度很长,跟你的 Vocabulary 的 Size 是一样的。

#### Vocabulary Size 则是什么意思?

你就先想好说,你的 Decoder 输出的单位是什么,假设我们今天做的是中文的语音辨识,我们 Decoder 输出的是中文,你这边的 Vocabulary 的 Size ,可能就是中文的方块字的数目。用 Subword 当作英文的单位,就有一些方法,可以把英文的字首字根切出来,拿字首字根当作单位,如果中文的话,我觉得就比较单纯,通常今天你可能就用中文的这个方块字,来当作单位。

每一个中文的字,都会对应到一个数值,因为在产生这个向量之前,你通常会先跑一个 Softmax,就跟做分类一样,所以这一个向量里面的分数,它是一个 Distribution,也就是,它这个向量里面的值,它全部加起来,总和 会是 1

分数最高的一个中文字,它就是最终的输出。在这个例子里面,机的分数最高,所以机,就当做是这个 Decoder 第一个输出。然后接下来,你把“机”当做是 Decoder 新的 Input,原来 Decoder 的 Input,只有 BEGIN 这个特别的符号,现在它除了 BEGIN 以外,它还有“机”作为它的 Input。

所以 Decoder 现在它有两个输入

• 一个是 BEGIN 这个符号
• 一个是“机”

根据这两个输入,它输出一个蓝色的向量,根据这个蓝色的向量里面,给每一个中文的字的分数,我们会决定第二个输出，哪一个字的分数最高,它就是输出,假设"器"的分数最高,"器"就是输出。

然后现在 Decoder

• 看到了 BEGIN
• 看到了"机"
• 看到了"器"

它接下来,还要再决定接下来要输出什么,它可能,就输出"学",这一个过程就反覆的持续下去

所以现在 Decode

• 看到了 BEGIN

• 看到了"机"

• 看到了"器"

• 还有"学"

Encoder 这边其实也有输入,等一下再讲 Encoder 的输入,Decoder 是怎么处理的,所以 Decoder 看到 Encoder 这边的输入,看到"机" 看到"器" 看到"学",决定接下来输出一个向量,这个向量里面,"习"这个中文字的分数最高的,所以它就输出"习"。

然后这个 Process ,就反覆持续下去,这边有一个关键的地方,我们特别用红色的虚线把它标出来。

Decoder 看到的输入,其实是它在前一个时间点自己的输出,Decoder 会把自己的输出,当做接下来的输入。

如果Decoder 看到错误的输入,让 Decoder 看到自己产生出来的错误的输入,再被 Decoder 自己吃进去,会不会造成 ==Error Propagation== 的问题.

Error Propagation 的问题就是,一步错 步步错这样,就是在这个地方,如果不小心把机器的“器”,不小心写成天气的"气",会不会接下来就整个句子都坏掉了,都没有办法再产生正确的词汇了?

有可能,这个等一下,我们最后会稍微讲一下,这个问题要怎么处理,我们现在,先无视这个问题,继续走下去

我们来看一下这个 Decoder内部的结构长什么样子?

那我们这边,把 Encoder 的部分先暂时省略掉,那在 Transformer 里面,Decoder 的结构,长得是这个样子的,看起来有点复杂,比 Encoder 还稍微复杂一点,那我们现在先把 Encoder 跟 Decoder 放在一起。

稍微比较一下它们之间的差异,那你会发现说,如果我们把 Decoder 中间这一块,中间这一块把它盖起来,其实 Encoder 跟 Decoder,并没有那么大的差别。

你看 Encoder 这边,Multi-Head Attention,然后 Add & Norm,Feed Forward,Add & Norm,重复 N 次,Decoder 其实也是一样。

当我们把中间这一块遮起来以后,我们等一下再讲,遮起来这一块里面做了什么事,但当我们把中间这块遮起来以后, 那 Decoder 也是,有一个 Multi-Head Attention,Add & Norm,然后 Feed Forward,然后 Add & Norm,所以 Encoder 跟 Decoder,其实并没有非常大的差别,除了中间这一块不一样的地方,那只是最后,我们可能会再做一个 Softmax,使得它的输出变成一个机率,那这边有一个稍微不一样的地方是,在 Decoder 这边,Multi-Head Attention 这一个 Block 上面,还加了一个 ==Masked==,

这个 Masked 的意思是这样子的,这是我们原来的 Self-Attention ，Input 一排 Vector,Output 另外一排 Vector,这一排 Vector 每一个输出,都要看过完整的 Input 以后,才做决定,所以输出 \(b^1\) 的时候,其实是根据 \(a^1\) 到 \(a^4\) 所有的资讯,去输出 \(b^1\)。

当我们把 Self-Attention,转成 Masked Attention 的时候,它的不同点是,现在我们不能再看右边的部分,也就是产生 \(b^1\) 的时候,我们只能考虑 \(a^1\) 的资讯,你不能够再考虑 \(a^2\) \(a^3\) \(a^4\)。产生 \(b^2\) 的时候,你只能考虑 \(a^1\) \(a^2\) 的资讯,不能再考虑 \(a^3\) \(a^4\) 的资讯。产生 \(b^3\) 的时候,你就不能考虑 \(a^4\) 的资讯。产生 \(b^4\) 的时候,你可以用整个 Input Sequence 的资讯,这个就是 Masked 的 Self-Attention。

讲得更具体一点,你做的事情是,当我们要产生 \(b^2\) 的时候,我们只拿第二个位置的 Query \(b^2\),去跟第一个位置的 Key,和第二个位置的 Key,去计算 Attention,第三个位置跟第四个位置,就不管它,不去计算 Attention。

我们这样子不去管这个 \(a^2\) 右边的地方,只考虑 \(a^1\) 跟 \(a^2\),只考虑 \(q^1\) \(q^2\),只考虑 \(k^1\) \(k^2\),\(q^2\) 只跟 \(k^1\) 跟 \(k^2\) 去计算 Attention,然后最后只计算 \(b^1\) 跟 \(b^2\) 的 Weighted Sum。然后当我们输出这个 \(b^2\) 的时候,\(b^2\) 就只考虑了 \(a^1\) 跟 \(a^2\),就没有考虑到 \(a^3\) 跟 \(a^4\)。

那为什么会这样,为什么需要加 Masked ？

这件事情其实非常地直觉:我们一开始 Decoder 的运作方式,它是一个一个输出,所以是先有 \(a^1\) 再有 \(a^2\),再有 \(a^3\) 再有 \(a^4\)。这跟原来的 Self-Attention 不一样,原来的 Self-Attention,\(a^1\) 跟 \(a^4\) 是一次整个输进去你的 Model 里面的,在我们讲 Encoder 的时候,Encoder 是一次把 \(a^1\) 跟 \(a^4\),都整个都读进去。但是对 Decoder 而言,先有 \(a^1\) 才有 \(a^2\),才有 \(a^3\) 才有 \(a^4\),所以实际上,当你有 \(a^2\),你要计算 \(b^2\) 的时候,你是没有 \(a^3\) 跟 \(a^4\) 的,所以你根本就没有办法把 \(a^3\) \(a^4\) 考虑进来。

所以这就是为什么,在那个 Decoder 的那个图上面,Transformer 原始的 Paper 特别跟你强调说,那不是一个一般的 Attention, 这是一个 Masked 的 Self-Attention,意思只是想要告诉你说,Decoder 它的 Tokent,它输出的东西是一个一个产生的,所以它只能考虑它左边的东西,它没有办法考虑它右边的东西。

讲了 Decoder 的运作方式,但是这边,还有一个非常关键的问题,Decoder 必须自己决定,输出的 Sequence 的长度

可是到底输出的 Sequence 的长度应该是多少,我们不知道。

你没有办法轻易的从输入的 Sequence 的长度,就知道输出的 Sequence 的长度是多少,并不是说,输入是 4 个向量,输出一定就是 4 个向量。这边在这个例子里面,输入跟输出的长度是一样的,但是你知道实际上在你真正的应用里面,并不是这样,输入跟输出长度的关係,是非常复杂的,我们其实是期待机器可以自己学到,今天给它一个 Input Sequence 的时候,Output 的 Sequence 应该要多长。

但在我们目前的这整个 Decoder的这个运作的机制里面,机器不知道它什么时候应该停下来,它产生完习以后,它还可以继续重复一模一样的 Process,就把习,当做输入,然后也许 Decoder ,就会接一个惯,然后接下来,就一直持续下去,永远都不会停下来。

我们要让 Decoder 做的事情,也是一样,要让它可以输出一个断,所以你要特别准备一个特别的符号,这个符号,就叫做断,我们这边,用 END 来表示这个特殊的符号。

所以除了所有中文的方块字,还有 BEGIN 以外,你还要准备一个特殊的符号,叫做"断",那其实在助教的程式里面,它是把 BEGIN 跟 END,就是开始跟这个断,用同一个符号来表示。

反正这个,这个 BEGIN 只会在输入的时候出现,断只会在输出的时候出现,所以在助教的程式里面,如果你仔细研究一下的话,会发现说 END 跟 BEGIN,用的其实是同一个符号,但你用不同的符号,也是完全可以的,也完全没有问题

所以我们现在,当把"习"当作输入以后,就 Decoder 看到 Encoder 输出的这个 Embedding,看到了 "BEGIN",然后"机" "器" "学" "习"以后,看到这些资讯以后 它要知道说,这个语音辨识的结果已经结束了,不需要再产生更多的词汇了。

它产生出来的向量END,就是断的那个符号,它的机率必须要是最大的,然后你就输出断这个符号,那整个运作的过程,整个 Decoder 产生 Sequence 的过程,就结束了这个就是 ==Autoregressive Decoder==,它运作的方式。

2.2 Decoder – Non-autoregressive (NAT)

Non-Autoregressive ,通常缩写成 NAT,所以有时候 Autoregressive 的 Model,也缩写成 AT,Non-Autoregressive 的 Model 是怎么运作的。先输入 BEGIN,然后出现 w1,然后再把 w1 当做输入,再输出 w2,直到输出 END 为止

那 ==NAT== 是这样,它不是依次产生。

就假设我们现在产生是中文的句子,它不是依次产生一个字,它是一次把整个句子都产生出来。NAT 的 Decoder可能吃的是一整排的 BEGIN 的 Token,你就把一堆一排 BEGIN 的 Token 都丢给它,让它一次产生一排 Token 就结束了

举例来说,如果你丢给它 4 个 BEGIN 的 Token,它就产生 4 个中文的字,变成一个句子,就结束了，所以它只要一个步骤,就可以完成句子的生成，这边你可能会问一个问题：刚才不是说不知道输出的长度应该是多少吗,那我们这边怎么知道 BEGIN 要放多少个,当做 NAT Decoder 的收入？

没错 这件事没有办法很自然的知道,没有办法很直接的知道,所以有几个,所以有几个做法

• 一个做法是,你另外learn一个 Classifier,这个 Classifier ,它吃 Encoder 的 Input,然后输出是一个数字,这个数字代表 Decoder 应该要输出的长度,这是一种可能的做法
• 另一种可能做法就是,你就不管三七二十一,给它一堆 BEGIN 的 Token,你就假设说,你现在输出的句子的长度,绝对不会超过 300 个字,你就假设一个句子长度的上限,然后 BEGIN ,你就给它 300 个 BEGIN,然后就会输出 300 个字嘛,然后,你再看看什么地方输出 END,输出 END 右边的,就当做它没有输出,就结束了,这是另外一种处理 NAT 的这个 Decoder,它应该输出的长度的方法

NAT 的 Decoder,最近它之所以是一个热门研究主题,就是它虽然表面上看起来有种种的厉害之处,尤其是平行化是它最大的优势,但是 NAT 的 Decoder ,它的 Performance,往往都不如 AT 的 Decoder。

2.3 Encoder-Decoder

接下来就要讲Encoder 跟 Decoder它们中间是怎么传递资讯的了,也就是我们要讲,刚才我们刻意把它遮起来的那一块。

这块叫做 ==Cross Attention==,它是连接 Encoder 跟 Decoder 之间的桥樑,那这一块里面啊,会发现有两个输入来自于 Encoder,Encoder 提供两个箭头,然后 Decoder 提供了一个箭头,所以从左边这两个箭头,Decoder 可以读到 Encoder 的输出。

那这个模组实际上是怎么运作的呢,那我们就实际把它运作的过程跟大家展示一下，这个是你的 Encoder：

输入一排向量,输出一排向量,我们叫它 \(a^1 a^2 a^3\)。

接下来 轮到你的 Decoder,你的 Decoder 呢,会先吃 BEGIN 当做,BEGIN 这个 Special 的 Token,那 BEGIN 这个 Special 的 Token 读进来以后,你可能会经过 Self-Attention,这个 Self-Attention 是有做 Mask 的,然后得到一个向量,就是 Self-Attention 就算是有做 Mask,还是一样输入多少长度的向量,输出就是多少向量。

所以输入一个向量 输出一个向量,然后接下来把这个向量呢,乘上一个矩阵做一个 Transform,得到一个 Query 叫做 q：

然后这边的 \(a^1 a^2 a^3\) 呢,也都产生 Key,Key1 Key2 Key3,那把这个 q 跟 \(k^1 k^2 k^3\),去计算 Attention 的分数,得到 \(α_1 α_2 α_3\),当然你可能一样会做 Softmax,把它稍微做一下 Normalization,所以我这边加一个 ',代表它可能是做过 Normalization。接下来再把 \(α_1 α_2 α_3\),就乘上 \(v^1 v^2 v^3\),再把它 Weighted Sum 加起来会得到 v。

那这一个 V,就是接下来会丢到 Fully-Connected 的,Network 做接下来的处理,那这个步骤就是 q 来自于 Decoder,k 跟 v 来自于 Encoder,这个步骤就叫做 Cross Attention。 Decoder 就是凭藉著产生一个 q,去 Encoder 这边抽取资讯出来,当做接下来的 Decoder 的,Fully-Connected 的 Network 的 Input。

当然这个,就现在假设产生第二个,第一个这个中文的字产生一个“机”,接下来的运作也是一模一样的。

输入 BEGIN 输入机,产生一个向量,这个向量一样乘上一个 Linear 的 Transform,得到 q',得到一个 Query,这个 Query 一样跟 \(k^1 k^2 k^3\),去计算 Attention 的分数,一样跟 \(v^1 v^2 v^3\) 做 Weighted Sum 做加权,然后加起来得到 v',交给接下来 Fully-Connected Network 做处理，所以这就是Cross Attention 的运作的过程。

也许有人会有疑问：那这个 Encoder 有很多层啊,Decoder 也有很多层啊,从刚才的讲解里面好像听起来,这个 Decoder 不管哪一层,都是拿 Encoder 的最后一层的输出这样对吗？

对,在原始 Paper 里面的实做是这样子,那一定要这样吗？

不一定要这样,你永远可以自己兜一些新的想法,所以我这边就是引用一篇论文告诉你说,也有人尝试不同的 Cross Attension 的方式。

Encoder 这边有很多层,Decoder 这边有很多层,为什么 Decoder 这边每一层都一定要看,Encoder 的最后一层输出呢,能不能够有各式各样不同的连接方式,这完全可以当做一个研究的问题来 Study。

2.4 Training

已经清楚说 Input 一个 Sequence,是怎么得到最终的输出,那接下来就进入训练的部分。

刚才讲的都还只是,假设你模型训练好以后它是怎么运作的,它是怎么做 Testing 的,它是怎么做 Inference 的,Inference 就是 Testing ，那是怎么做训练的呢？

接下来就要讲怎么做训练,那如果是做语音辨识,那你要有训练资料,你要收集一大堆的声音讯号,每一句声音讯号都要有工读生来听打一下,打出说它的这个对应的词汇是什么？

工读生听这段是机器学习,他就把机器学习四个字打出来,所以就知道说你的这个 Transformer,应该要学到 听到这段声音讯号,它的输出就是机器学习这四个中文字。

那怎么让机器学到这件事呢? 我们已经知道说输入这段声音讯号,第一个应该要输出的中文字是“机”,所以今天当我们把 BEGIN,丢给这个 Encoder 的时候,它第一个输出应该要跟“机”越接近越好。

“机”这个字会被表示成一个 One-Hot 的 Vector,在这个 Vector 里面,只有机对应的那个维度是 1,其他都是 0,这是正确答案,那我们的 Decoder,它的输出是一个 Distribution,是一个机率的分布,我们会希望这一个机率的分布,跟这个 One-Hot 的 Vector 越接近越好。所以你会去计算这个 Ground Truth,跟这个 Distribution 它们之间的 Cross Entropy,然后我们希望这个 ==Cross Entropy== 的值,越小越好。

它就跟分类很像,刚才助教在讲解作业的时候也有提到这件事情,你可以想成每一次我们在产生,每一次 Decoder 在产生一个中文字的时候,其实就是做了一次分类的问题,中文字假设有四千个,那就是做有四千个类别的分类的问题

所以实际上训练的时候这个样子,我们已经知道输出应该是“机器学习”这四个字,就告诉你的 Decoder ,现在你第一次的输出 第二次的输出,第三次的输出 第四次输出,应该分别就是“机” “器” “学”跟“习”,这四个中文字的 One-Hot Vector,我们希望我们的输出,跟这四个字的 One-Hot Vector 越接近越好。

在训练的时候,每一个输出都会有一个 Cross Entropy,每一个输出跟 One-Hot Vector,跟它对应的正确答案都有一个 Cross Entropy,我们要希望所有的 Cross Entropy 的总和最小越小越好。所以这边做了四次分类的问题,我们希望这些分类的问题,它总合起来的 Cross Entropy 越小越好,还有 END 这个符号。

那这个就是 Decoder 的训练，把 Ground Truth ,正确答案给它,希望 Decoder 的输出跟正确答案越接近越好。

那这边有一件值得我们注意的事情,在训练的时候我们会给 Decoder 看正确答案,也就是我们会告诉它说

• 在已经有 "BEGIN",在有"机"的情况下你就要输出"器"
• 有 "BEGIN" 有"机" 有"器"的情况下输出"学"
• 有 "BEGIN" 有"机" 有"器" 有"学"的情况下输出"习"
• 有 "BEGIN" 有"机" 有"器" 有"学" 有"习"的情况下,你就要输出"断"

在 Decoder 训练的时候,我们会在输入的时候给它正确的答案,那这件事情叫做 ==Teacher Forcing==

那这个时候你马上就会有一个问题了？

• 训练的时候,Decoder 有偷看到正确答案了
• 但是测试的时候,显然没有正确答案可以给 Decoder 看

刚才也有强调说在真正使用这个模型,在 Inference 的时候,Decoder 看到的是自己的输入,这中间显然有一个 ==Mismatch==,那等一下我们会有一页投影片的说明,有什么样可能的解决方式。

2.5 Tips

那接下来,不侷限于 Transformer ,讲一些训练这种 Sequence To Sequence Model 的Tips

Copy Mechanism

在我们刚才的讨论里面,我们都要求 Decoder 自己产生输出,但是对很多任务而言,也许 Decoder 没有必要自己创造输出出来,它需要做的事情,也许是从输入的东西里面复製一些东西出来。

像这种复製的行为在哪些任务会用得上呢,一个例子是做聊天机器人。

• 人对机器说:你好 我是库洛洛,

• 机器应该回答说:库洛洛你好 很高兴认识你

对机器来说,它其实没有必要创造库洛洛这个词汇,这对机器来说一定会是一个非常怪异的词汇,所以它可能很难,在训练资料里面可能一次也没有出现过,所以它不太可能正确地产生这段词汇出来。

但是假设今天机器它在学的时候,它学到的是看到输入的时候说我是某某某,就直接把某某某,不管这边是什么复製出来说某某某你好。

那这样子机器的训练显然会比较容易,它显然比较有可能得到正确的结果,所以复製对于对话来说,可能是一个需要的技术 需要的能力。

Guided Attention

机器就是一个黑盒子,有时候它里面学到什么东西,你实在是搞不清楚,那有时候它会犯非常低级的错误。但是对语音辨识 语音合成,Guiding Attention,可能就是一个比较重要的技术。

Guiding Attention 要做的事情就是,要求机器它在做 Attention 的时候,是有固定的方式的,举例来说,对语音合成或者是语音辨识来说,我们想像中的 Attention,应该就是由左向右。

在这个例子里面,我们用红色的这个曲线,来代表 Attention 的分数,这个越高就代表 Attention 的值越大

我们以语音合成为例,那你的输入就是一串文字,那你在合成声音的时候,显然是由左念到右,所以机器应该是,先看最左边输入的词汇产生声音,再看中间的词汇产生声音,再看右边的词汇产生声音

如果你今天在做语音合成的时候,你发现机器的 Attention,是颠三倒四的,它先看最后面,接下来再看前面,那再胡乱看整个句子,那显然有些是做错了,显然有些是,Something is wrong,有些是做错了,

所以 Guiding Attention 要做的事情就是,强迫 Attention 有一个固定的样貌,那如果你对这个问题,本身就已经有理解知道说,语音合成 TTS 这样的问题,你的 Attention 的分数,Attention 的位置都应该由左向右,那不如就直接把这个限制,放进你的 Training 里面,要求机器学到 Attention,就应该要由左向右。

Optimizing Evaluation Metrics?

在作业里面,我们评估的标准用的是,BLEU Score,BLEU Score 是你的 Decoder,先产生一个完整的句子以后,再去跟正确的答案一整句做比较,我们是拿两个句子之间做比较,才算出 BLEU Score。

但我们在训练的时候显然不是这样,训练的时候,每一个词汇是分开考虑的,训练的时候,我们 Minimize 的是 Cross Entropy,Minimize Cross Entropy,真的可以 Maximize BLEU Score 吗？

不一定,因为这两个根本就是,它们可能有一点点的关联,但它们又没有那么直接相关,它们根本就是两个不同的数值,所以我们 Minimize Cross Entropy,不见得可以让 BLEU Score 比较大。

所以你发现说在助教的程式里面,助教在做 Validation 的时候,并不是拿 Cross Entropy 来挑最好的 Model,而是挑 BLEU Score 最高的那一个 Model,所以我们训练的时候,是看 Cross Entropy,但是我们实际上你作业真正评估的时候,看的是 BLEU Score,所以你 Validation Set,其实应该考虑用 BLEU Score。

那接下来有人就会想说,那我们能不能在 Training 的时候,就考虑 BLEU Score 呢,我们能不能够训练的时候就说,我的 Loss 就是,BLEU Score 乘一个负号,那我们要 Minimize 那个 Loss,假设你的 Loss 是,BLEU Score乘一个负号,它也等于就是 Maximize BLEU Score。但是这件事实际上没有那么容易,你当然可以把 BLEU Score,当做你训练的时候,你要最大化的一个目标,但是 BLEU Score 本身很复杂,它是不能微分的。

这边之所以採用 Cross Entropy,而且是每一个中文的字分开来算,就是因为这样我们才有办法处理,如果你是要计算,两个句子之间的 BLEU Score,这一个 Loss,根本就没有办法做微分,那怎么办呢？这边就教大家一个口诀,遇到你在 Optimization 无法解决的问题,==用 RL 硬 Train 一发==就对了这样,遇到你无法 Optimize 的 Loss Function,把它当做是 RL 的 Reward,把你的 Decoder 当做是 Agent,它当作是 RL,Reinforcement Learning 的问题硬做。

Scheduled Sampling （计划采样）

那我们要讲到,我们刚才反覆提到的问题了,就是训练跟测试居然是不一致的

测试的时候,Decoder 看到的是自己的输出,所以测试的时候,Decoder 会看到一些错误的东西,但是在训练的时候,Decoder 看到的是完全正确的,那这个不一致的现象叫做,==Exposure Bias==。

假设 Decoder 在训练的时候,永远只看过正确的东西,那在测试的时候,你只要有一个错,那就会一步错 步步错,因为对 Decoder 来说,它从来没有看过错的东西,它看到错的东西会非常的惊奇,然后接下来它产生的结果可能都会错掉。

所以要怎么解决这个问题呢？

有一个可以的思考的方向是,给 Decoder 的输入加一些错误的东西,就这么直觉,你不要给 Decoder 都是正确的答案,偶尔给它一些错的东西,它反而会学得更好,这一招叫做,==Scheduled Sampling==,它不是那个 Schedule Learning Rate,刚才助教有讲 Schedule Learning Rate,那是另外一件事,不相干的事情,这个是 Scheduled Sampling。

Scheduled Sampling 其实很早就有了,这个是 15 年的 Paper,很早就有 Scheduled Sampling,在还没有 Transformer,只有 LSTM 的时候,就已经有 Scheduled Sampling,但是 Scheduled Sampling 这一招,它其实会伤害到,Transformer 的平行化的能力,那细节可以再自己去了解一下,所以对 Transformer 来说,它的 Scheduled Sampling,另有招数跟传统的招数,跟原来最早提在,这个 LSTM上被提出来的招数,也不太一样,那我把一些 Reference 的,列在这边给大家参考。

Transformer 和种种的训练技巧,这个我们已经讲完了 Encoder,讲完了 Decoder,也讲完了它们中间的关係,也讲了怎么训练,也讲了种种的 Tip。

Transformer

Transformer：（Self-attention）自注意力机制的序列到序列的模型

• Transformer 代码完全解读!
• 如何从浅入深理解transformer？
• Transformer和GNN有什么联系吗？
• 详解Transformer （Attention Is All You Need）
• Transformer代码+面试细节

一、模型结构概述

如下是Transformer的两个结构示意图：

上图是从一篇英文博客中截取的Transformer的结构简图，下图是原论文中给出的结构简图，更细粒度一些，可以结合着来看。

模型大致分为Encoder(编码器)和Decoder(解码器)两个部分，分别对应上图中的左右两部分。

编码器由N个相同的层堆叠在一起(我们后面的实验取N=6)，每一层又有两个子层：

• 第一个子层是一个Multi-Head Attention(==多头的自注意机制==)
  • Self-attention多个头类似于cnn中多个卷积核的作用，使用多头注意力，能够从不同角度提取信息，提高信息提取的全面性。
• 第二个子层是一个简单的Feed Forward(全连接前馈网络)
• 两个子层都添加了一个残差连接+==layer normalization==的操作。

解码器同样是堆叠了N个相同的层，不过和编码器中每层的结构稍有不同。

• 第一个子层是一个Multi-Head Attention(==多头的自注意机制==)
• 第二个子层是一个简单的Feed Forward(全连接前馈网络)
• ==Masked Multi-Head Attention==
• 每个子层同样也用了==residual==以及layer normalization。

模型的输入由Input Embedding和Positional Encoding(位置编码)两部分组合而成。

模型的输出由Decoder的输出简单的经过softmax得到。

二、模型输入

首先我们来看模型的输入是什么样的，先明确模型输入，后面的模块理解才会更直观。输入部分包含两个模块，Embedding和Positional Encoding。

2.1 Embedding层

Embedding层的作用是将某种格式的输入数据，例如文本，转变为模型可以处理的向量表示，来描述原始数据所包含的信息。Embedding层输出的可以理解为当前时间步的特征，如果是文本任务，这里就可以是Word Embedding，如果是其他任务，就可以是任何合理方法所提取的特征。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        """
        类的初始化函数
        d_model：指词嵌入的维度
        vocab:指词表的大小
        """
        super(Embeddings, self).__init__()
        #之后就是调用nn中的预定义层Embedding，获得一个词嵌入对象self.lut
        self.lut = nn.Embedding(vocab, d_model)
        #最后就是将d_model传入类中
        self.d_model =d_model
    def forward(self, x):
        """
        Embedding层的前向传播逻辑
        参数x：这里代表输入给模型的单词文本通过词表映射后的one-hot向量
        将x传给self.lut并与根号下self.d_model相乘作为结果返回
        """
        embedds = self.lut(x)
        return embedds * math.sqrt(self.d_model)

2.2 位置编码

Positional Encodding位置编码的作用是为模型提供当前时间步的前后出现顺序的信息。因为Transformer不像RNN那样的循环结构有前后不同时间步输入间天然的先后顺序，所有的时间步是同时输入，并行推理的，因此在时间步的特征中融合进位置编码的信息是合理的。位置编码可以有很多选择，可以是固定的，也可以设置成可学习的参数。这里，我们使用固定的位置编码。具体地，使用不同频率的sin和cos函数来进行位置编码，如下所示： \[ \begin{gathered} P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \end{gathered} \] 其中pos代表时间步的下标索引，向量也就是第pos个时间步的位置编码，编码长度同Embedding层，这里我们设置的是512。上面有两个公式，代表着位置编码向量中的元素，奇数位置和偶数位置使用两个不同的公式。思考：为什么上面的公式可以作为位置编码？我的理解：在上面公式的定义下， 时间步p和时间步p+k的位置编码的内积，即是与p无关，只与k有关的定值（不妨自行证明下试试）。也就是说，任意两个相距k个时间步的位置编码向量的内积都是相同的，这就相当于蕴含了两个时间步之间相对位置关系的信息。此外，每个时间步的位置编码又是唯一的，这两个很好的性质使得上面的公式作为位置编码是有理论保障的。下面是位置编码模块的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        """
        位置编码器类的初始化函数
        
        共有三个参数，分别是
        d_model：词嵌入维度
        dropout: dropout触发比率
        max_len：每个句子的最大长度
        """
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings
        # 注意下面代码的计算方式与公式中给出的是不同的，但是是等价的，你可以尝试简单推导证明一下。
        # 这样计算是为了避免中间的数值计算结果超出float的范围，
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)

因此，可以认为，最终模型的输入是若干个时间步对应的embedding，每一个时间步对应一个embedding，可以理解为是当前时间步的一个综合的特征信息，即包含了本身的语义信息，又包含了当前时间步在整个句子中的位置信息。

2.3 Encoder和Decoder都包含输入模块

此外有一个点刚刚接触Transformer的同学可能不太理解，编码器和解码器两个部分都包含输入，且两部分的输入的结构是相同的，只是推理时的用法不同，编码器只推理一次，而解码器是类似RNN那样循环推理，不断生成预测结果的。

怎么理解？假设我们现在做的是一个法语-英语的机器翻译任务，想把Je suis étudiant翻译为I am a student。那么我们输入给编码器的就是时间步数为3的embedding数组，编码器只进行一次并行推理，即获得了对于输入的法语句子所提取的若干特征信息。而对于解码器，是循环推理，逐个单词生成结果的。最开始，由于什么都还没预测，我们会将编码器提取的特征，以及一个句子起始符传给解码器，解码器预期会输出一个单词I。然后有了预测的第一个单词，我们就将I输入给解码器，会再预测出下一个单词am，再然后我们将I am作为输入喂给解码器，以此类推直到预测出句子终止符完成预测。

三、Encoder

3.1 编码器

编码器作用是用于对输入进行特征提取，为解码环节提供有效的语义信息整体来看编码器由N个编码器层简单堆叠而成，因此实现非常简单，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 定义一个clones函数，来更方便的将某个结构复制若干份
def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

class Encoder(nn.Module):
    """
    Encoder
    The encoder is composed of a stack of N=6 identical layers.
    """
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        # 调用时会将编码器层传进来，我们简单克隆N分，叠加在一起，组成完整的Encoder
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

上面的代码中有一个小细节，就是编码器的输入除了x，也就是embedding以外，还有一个mask，为了介绍连续性，这里先忽略，后面会讲解。下面我们来看看单个的编码器层都包含什么，如何实现。

3.2 编码器层

每个编码器层由两个子层连接结构组成：第一个子层包括一个多头自注意力层和规范化层以及一个残差连接；第二个子层包括一个前馈全连接层和规范化层以及一个残差连接；如下图所示：

可以看到，两个子层的结构其实是一致的，只是中间核心层的实现不同

我们先定义一个SubLayerConnection类来描述这种结构关系:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class SublayerConnection(nn.Module):
    """ 
    实现子层连接结构的类
    """
    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):

        # 原paper的方案
        #sublayer_out = sublayer(x)
        #x_norm = self.norm(x + self.dropout(sublayer_out))

        # 稍加调整的版本
        sublayer_out = sublayer(x)
        sublayer_out = self.dropout(sublayer_out)
        x_norm = x + self.norm(sublayer_out)
        return x_norm

注：上面的实现中，我对残差的链接方案进行了小小的调整，和原论文有所不同。把x从norm中拿出来，保证永远有一条“高速公路”，这样理论上会收敛的快一些，但我无法确保这样做一定是对的，请一定注意。定义好了SubLayerConnection，我们就可以实现EncoderLayer的结构了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class EncoderLayer(nn.Module):
    "EncoderLayer is made up of two sublayer: self-attn and feed forward"                                                                                                         
    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size   # embedding's dimention of model, 默认512

    def forward(self, x, mask):
        # attention sub layer
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        # feed forward sub layer
        z = self.sublayer[1](x, self.feed_forward)
        return z

继续往下拆解，我们需要了解 attention层 和 feed_forward层的结构以及如何实现。

3.3 注意力机制 Self-Attention

人类在观察事物时，无法同时仔细观察眼前的一切，只能聚焦到某一个局部。通常我们大脑在简单了解眼前的场景后，能够很快把注意力聚焦到最有价值的局部来仔细观察，从而作出有效判断。或许是基于这样的启发，大家想到了在算法中利用注意力机制。注意力计算：它需要三个指定的输入Q（query），K（key），V（value），然后通过下面公式得到注意力的计算结果。

• 

• 相似度计算 ： 与 运算，得到 矩阵，复杂度为
• softmax计算：对每行做softmax，复杂度为 ，则n行的复杂度为
• 加权和： 与 运算，得到 矩阵，复杂度为

故最后self-attention的时间复杂度为 ; 对于受限的self-attention，每个元素仅能和周围 个元素进行交互，即和 个 维向量做内积运算，复杂度为 ，则 个元素的总时间复杂度为

计算流程图如下：

可以这么简单的理解，当前时间步的注意力计算结果，是一个组系数 * 每个时间步的特征向量value的累加，而这个系数，通过当前时间步的query和其他时间步对应的key做内积得到，这个过程相当于用自己的query对别的时间步的key做查询，判断相似度，决定以多大的比例将对应时间步的信息继承过来。下面是注意力模块的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    #首先取query的最后一维的大小，对应词嵌入维度
    d_k = query.size(-1)
    #按照注意力公式，将query与key的转置相乘，这里面key是将最后两个维度进行转置，再除以缩放系数得到注意力得分张量scores
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    #接着判断是否使用掩码张量
    if mask is not None:
        #使用tensor的masked_fill方法，将掩码张量和scores张量每个位置一一比较，如果掩码张量则对应的scores张量用-1e9这个置来替换
        scores = scores.masked_fill(mask == 0, -1e9)
    #对scores的最后一维进行softmax操作，使用F.softmax方法，这样获得最终的注意力张量
    p_attn = F.softmax(scores, dim = -1)
    #之后判断是否使用dropout进行随机置0
    if dropout is not None:
        p_attn = dropout(p_attn)
    #最后，根据公式将p_attn与value张量相乘获得最终的query注意力表示，同时返回注意力张量
    return torch.matmul(p_attn, value), p_attn

3.4 多头注意力机制

刚刚介绍了attention机制，在搭建EncoderLayer时候所使用的Attention模块，实际使用的是多头注意力，可以简单理解为多个注意力模块组合在一起。

多头注意力机制的作用：这种结构设计能让每个注意力机制去优化每个词汇的不同特征部分，从而均衡同一种注意力机制可能产生的偏差，让词义拥有来自更多元表达，实验表明可以从而提升模型效果。

对于multi-head attention，假设有 个head，这里 是一个常数，对于每个head，首先需要把三个矩阵分别映射到 维度。这里考虑一种简化情况： 。(对于dot-attention计算方式， 与 可以不同)。

• 输入线性映射的复杂度： 与 运算，忽略常系数，复杂度为 。
• Attention操作复杂度：主要在相似度计算及加权和的开销上， 与 运算，复杂度为
• 输出线性映射的复杂度：concat操作拼起来形成 的矩阵，然后经过输出线性映射，保证输入输出相同，所以是 与 计算，复杂度为

故最后的复杂度为：

举个更形象的例子，bank是银行的意思，如果只有一个注意力模块，那么它大概率会学习去关注类似money、loan贷款这样的词。如果我们使用多个多头机制，那么不同的头就会去关注不同的语义，比如bank还有一种含义是河岸，那么可能有一个头就会去关注类似river这样的词汇，这时多头注意力的价值就体现出来了。下面是多头注意力机制的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        #在类的初始化时，会传入三个参数，h代表头数，d_model代表词嵌入的维度，dropout代表进行dropout操作时置0比率，默认是0.1
        super(MultiHeadedAttention, self).__init__()
        #在函数中，首先使用了一个测试中常用的assert语句，判断h是否能被d_model整除，这是因为我们之后要给每个头分配等量的词特征，也就是embedding_dim/head个
        assert d_model % h == 0
        #得到每个头获得的分割词向量维度d_k
        self.d_k = d_model // h
        #传入头数h
        self.h = h
        
        #创建linear层，通过nn的Linear实例化，它的内部变换矩阵是embedding_dim x embedding_dim，然后使用，为什么是四个呢，这是因为在多头注意力中，Q,K,V各需要一个，最后拼接的矩阵还需要一个，因此一共是四个
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        #self.attn为None，它代表最后得到的注意力张量，现在还没有结果所以为None
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        #前向逻辑函数，它输入参数有四个，前三个就是注意力机制需要的Q,K,V，最后一个是注意力机制中可能需要的mask掩码张量，默认是None
        if mask is not None:
            # Same mask applied to all h heads.
            #使用unsqueeze扩展维度，代表多头中的第n头
            mask = mask.unsqueeze(1)
        #接着，我们获得一个batch_size的变量，他是query尺寸的第1个数字，代表有多少条样本
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        # 首先利用zip将输入QKV与三个线性层组到一起，然后利用for循环，将输入QKV分别传到线性层中，做完线性变换后，开始为每个头分割输入，这里使用view方法对线性变换的结构进行维度重塑，多加了一个维度h代表头，这样就意味着每个头可以获得一部分词特征组成的句子，其中的-1代表自适应维度，计算机会根据这种变换自动计算这里的值，然后对第二维和第三维进行转置操作，为了让代表句子长度维度和词向量维度能够相邻，这样注意力机制才能找到词义与句子位置的关系，从attention函数中可以看到，利用的是原始输入的倒数第一和第二维，这样我们就得到了每个头的输入
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]

        # 2) Apply attention on all the projected vectors in batch. 
        # 得到每个头的输入后，接下来就是将他们传入到attention中，这里直接调用我们之前实现的attention函数，同时也将mask和dropout传入其中
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)

        # 3) "Concat" using a view and apply a final linear. 
        # 通过多头注意力计算后，我们就得到了每个头计算结果组成的4维张量，我们需要将其转换为输入的形状以方便后续的计算，因此这里开始进行第一步处理环节的逆操作，先对第二和第三维进行转置，然后使用contiguous方法。这个方法的作用就是能够让转置后的张量应用view方法，否则将无法直接使用，所以，下一步就是使用view重塑形状，变成和输入形状相同。  
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        #最后使用线性层列表中的最后一个线性变换得到最终的多头注意力结构的输出
        return self.linears[-1](x)

3.5 前馈全连接层

EncoderLayer中另一个核心的子层是 Feed Forward Layer，我们这就介绍一下。在进行了Attention操作之后，encoder和decoder中的每一层都包含了一个全连接前向网络，对每个position的向量分别进行相同的操作，包括两个线性变换和一个ReLU激活输出：

Feed Forward Layer 其实就是简单的由两个前向全连接层组成，核心在于，Attention模块每个时间步的输出都整合了所有时间步的信息，==而Feed Forward Layer每个时间步只是对自己的特征的一个进一步整合，与其他时间步无关。==

1
2
3
4
5
6
7
8
9
10
11

class PositionwiseFeedForward(nn.Module):
    def __init__(self, d_model, d_ff, dropout=0.1):
        #初始化函数有三个输入参数分别是d_model，d_ff，和dropout=0.1，第一个是线性层的输入维度也是第二个线性层的输出维度，因为我们希望输入通过前馈全连接层后输入和输出的维度不变，第二个参数d_ff就是第二个线性层的输入维度和第一个线性层的输出，最后一个是dropout置0比率。
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        #输入参数为x，代表来自上一层的输出，首先经过第一个线性层，然后使用F中的relu函数进行激活，之后再使用dropout进行随机置0，最后通过第二个线性层w2，返回最终结果
        return self.w_2(self.dropout(F.relu(self.w_1(x))))

到这里Encoder中包含的主要结构就都介绍了，上面的代码中涉及了两个小细节还没有介绍，layer normalization 和 mask，下面来简单讲解一下。

3.6. 规范化层

规范化层的作用：它是所有深层网络模型都需要的标准网络层，因为随着网络层数的增加，通过多层的计算后输出可能开始出现过大或过小的情况，这样可能会导致学习过程出现异常，模型可能收敛非常慢。因此都会在一定层后接规范化层进行数值的规范化，使其特征数值在合理范围内。Transformer中使用的normalization手段是layer norm，实现代码很简单，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."
    def __init__(self, feature_size, eps=1e-6):
        #初始化函数有两个参数，一个是features,表示词嵌入的维度,另一个是eps它是一个足够小的数，在规范化公式的分母中出现,防止分母为0，默认是1e-6。
        super(LayerNorm, self).__init__()
        #根据features的形状初始化两个参数张量a2，和b2，第一初始化为1张量，也就是里面的元素都是1，第二个初始化为0张量，也就是里面的元素都是0，这两个张量就是规范化层的参数。因为直接对上一层得到的结果做规范化公式计算，将改变结果的正常表征，因此就需要有参数作为调节因子，使其即能满足规范化要求，又能不改变针对目标的表征，最后使用nn.parameter封装，代表他们是模型的参数
        self.a_2 = nn.Parameter(torch.ones(feature_size))
        self.b_2 = nn.Parameter(torch.zeros(feature_size))
        #把eps传到类中
        self.eps = eps
    def forward(self, x):
    #输入参数x代表来自上一层的输出，在函数中，首先对输入变量x求其最后一个维度的均值，并保持输出维度与输入维度一致，接着再求最后一个维度的标准差，然后就是根据规范化公式，用x减去均值除以标准差获得规范化的结果。
    #最后对结果乘以我们的缩放参数，即a2,*号代表同型点乘，即对应位置进行乘法操作，加上位移参b2，返回即可
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

3.7 掩码及其作用

掩码：掩代表遮掩，码就是我们张量中的数值，它的尺寸不定，里面一般只有0和1；代表位置被遮掩或者不被遮掩。掩码的作用： 在transformer中，掩码主要的作用有两个，一个是屏蔽掉无效的padding区域，一个是屏蔽掉来自“未来”的信息。

Encoder中的掩码主要是起到第一个作用，Decoder中的掩码则同时发挥着两种作用。屏蔽掉无效的padding区域：我们训练需要组batch进行，就以机器翻译任务为例，一个batch中不同样本的输入长度很可能是不一样的，此时我们要设置一个最大句子长度，然后对空白区域进行padding填充，而填充的区域无论在Encoder还是Decoder的计算中都是没有意义的，因此需要用mask进行标识，屏蔽掉对应区域的响应。屏蔽掉来自未来的信息：我们已经学习了attention的计算流程，它是会综合所有时间步的计算的，那么在解码的时候，就有可能获取到未来的信息，这是不行的。因此，这种情况也需要我们使用mask进行屏蔽。现在还没介绍到Decoder，如果没完全理解，可以之后再回过头来思考下。mask的构造代码如下：

1
2
3
4
5
6
7
8
9
10

def subsequent_mask(size):
    #生成向后遮掩的掩码张量，参数size是掩码张量最后两个维度的大小，它最后两维形成一个方阵
    "Mask out subsequent positions."
    attn_shape = (1, size, size)
    #然后使用np.ones方法向这个形状中添加1元素，形成上三角阵
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    #最后将numpy类型转化为torch中的tensor，内部做一个1- 的操作。这个其实是做了一个三角阵的反转，subsequent_mask中的每个元素都会被1减。
    #如果是0，subsequent_mask中的该位置由0变成1
    #如果是1，subsequect_mask中的该位置由1变成0
    return torch.from_numpy(subsequent_mask) == 0

以上便是编码器部分的全部内容，有了这部分内容的铺垫，解码器的介绍就会轻松一些。

四、 Decoder

4.1 解码器整体结构

解码器的作用：根据编码器的结果以及上一次预测的结果，输出序列的下一个结果。整体结构上，解码器也是由N个相同层堆叠而成。构造代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

#使用类Decoder来实现解码器
class Decoder(nn.Module):
    "Generic N layer decoder with masking."
    def __init__(self, layer, N):
        #初始化函数的参数有两个，第一个就是解码器层layer，第二个是解码器层的个数N
        super(Decoder, self).__init__()
        #首先使用clones方法克隆了N个layer，然后实例化一个规范化层，因为数据走过了所有的解码器层后最后要做规范化处理。
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
    def forward(self, x, memory, src_mask, tgt_mask):
        #forward函数中的参数有4个，x代表目标数据的嵌入表示，memory是编码器层的输出，source_mask，target_mask代表源数据和目标数据的掩码张量，然后就是对每个层进行循环，当然这个循环就是变量x通过每一个层的处理，得出最后的结果，再进行一次规范化返回即可。
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

4.2 解码器层

每个解码器层由三个子层连接结构组成，第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接，第二个子层连接结构包括一个多头注意力子层和规范化层以及一个残差连接，第三个子层连接结构包括一个前馈全连接子层和规范化层以及一个残差连接。

解码器层中的各个子模块，如，多头注意力机制，规范化层，前馈全连接都与编码器中的实现相同。

有一个细节需要注意，第一个子层的多头注意力和编码器中完全一致， 第二个子层，它的多头注意力模块中，query来自上一个子层，key 和 value 来自编码器的输出。可以这样理解，就是第二层负责，利用解码器已经预测出的信息作为query，去编码器提取的各种特征中，查找相关信息并融合到当前特征中，来完成预测。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#使用DecoderLayer的类实现解码器层
class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"
    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        #初始化函数的参数有5个，分别是size，代表词嵌入的维度大小，同时也代表解码器的尺寸，第二个是self_attn，多头自注意力对象，也就是说这个注意力机制需要Q=K=V，第三个是src_attn,多头注意力对象，这里Q!=K=V，第四个是前馈全连接层对象，最后就是dropout置0比率
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        #按照结构图使用clones函数克隆三个子层连接对象
        self.sublayer = clones(SublayerConnection(size, dropout), 3)
 
    def forward(self, x, memory, src_mask, tgt_mask):
        #forward函数中的参数有4个，分别是来自上一层的输入x，来自编码器层的语义存储变量memory，以及源数据掩码张量和目标数据掩码张量，将memory表示成m之后方便使用。
        "Follow Figure 1 (right) for connections."
        m = memory
        #将x传入第一个子层结构，第一个子层结构的输入分别是x和self-attn函数，因为是自注意力机制，所以Q,K,V都是x，最后一个参数时目标数据掩码张量，这时要对目标数据进行遮掩，因为此时模型可能还没有生成任何目标数据。
        #比如在解码器准备生成第一个字符或词汇时，我们其实已经传入了第一个字符以便计算损失，但是我们不希望在生成第一个字符时模型能利用这个信息，因此我们会将其遮掩，同样生成第二个字符或词汇时，模型只能使用第一个字符或词汇信息，第二个字符以及之后的信息都不允许被模型使用。
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        #接着进入第二个子层，这个子层中常规的注意力机制，q是输入x;k,v是编码层输出memory，同样也传入source_mask，但是进行源数据遮掩的原因并非是抑制信息泄露，而是遮蔽掉对结果没有意义的padding。
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        #最后一个子层就是前馈全连接子层，经过它的处理后就可以返回结果，这就是我们的解码器结构
        return self.sublayer[2](x, self.feed_forward)

五、模型输出

输出部分就很简单了，每个时间步都过一个 线性层 + softmax层

线性层的作用：通过对上一步的线性变化得到指定维度的输出，也就是转换维度的作用。转换后的维度对应着输出类别的个数，如果是翻译任务，那就对应的是文字字典的大小。

六、模型构建

下面是Transformer总体架构图，回顾一下，再看这张图，是不是每个模块的作用都有了基本的认知。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

# Model Architecture
#使用EncoderDecoder类来实现编码器-解码器结构
class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. 
    Base for this and many other models.
    """
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        #初始化函数中有5个参数，分别是编码器对象，解码器对象,源数据嵌入函数，目标数据嵌入函数，以及输出部分的类别生成器对象.
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed    # input embedding module(input embedding + positional encode)
        self.tgt_embed = tgt_embed    # ouput embedding module
        self.generator = generator    # output generation module
        
    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        #在forward函数中，有四个参数，source代表源数据，target代表目标数据,source_mask和target_mask代表对应的掩码张量,在函数中，将source source_mask传入编码函数，得到结果后与source_mask target 和target_mask一同传给解码函数
        memory = self.encode(src, src_mask)
        res = self.decode(memory, src_mask, tgt, tgt_mask)
        return res
    
    def encode(self, src, src_mask):
        #编码函数，以source和source_mask为参数,使用src_embed对source做处理，然后和source_mask一起传给self.encoder
        src_embedds = self.src_embed(src)
        return self.encoder(src_embedds, src_mask)
    
    def decode(self, memory, src_mask, tgt, tgt_mask):
        #解码函数，以memory即编码器的输出，source_mask target target_mask为参数,使用tgt_embed对target做处理，然后和source_mask,target_mask,memory一起传给self.decoder
        target_embedds = self.tgt_embed(tgt)
        return self.decoder(target_embedds, memory, src_mask, tgt_mask)


# Full Model
def make_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1):
    """
    构建模型
    params:
        src_vocab:
        tgt_vocab:
        N: 编码器和解码器堆叠基础模块的个数
        d_model: 模型中embedding的size，默认512
        d_ff: FeedForward Layer层中embedding的size，默认2048
        h: MultiHeadAttention中多头的个数，必须被d_model整除
        dropout:
    """
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab))
    
    # This was important from their code. 
    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform_(p)
    return model

Transformer Q&A

3，Transformer的Feed Forward层在训练的时候到底在训练什么？ - zzzzzzz的回答 - 知乎 https://www.zhihu.com/question/499274875/answer/2250085650

Feed forward network (FFN)的作用？

Transformer在抛弃了 LSTM 结构后，FFN 中的激活函数成为了一个主要的提供非线性变换的单元。

GELU原理？相比RELU的优点？

ReLU会确定性的将输入乘上一个0或者1(当x<0时乘上0，否则乘上1)，Dropout则是随机乘上0。而GELU虽然也是将输入乘上0或1，但是输入到底是乘以0还是1，是在取决于输入自身的情况下随机选择的。

什么意思呢？具体来说：

我们将神经元的输入 乘上一个服从伯努利分布的 。而该伯努利分布又是依赖于 的：

其中， ，那么 就是标准正态分布的累积分布函数。这么做的原因是因为神经元的输入 往往遵循正态分布，尤其是深度网络中普遍存在Batch Normalization的情况下。当减小时，的值也会减小，此时被“丢弃”的可能性更高。所以说这是随机依赖于输入的方式。

现在，给出GELU函数的形式：

其中 是上文提到的标准正态分布的累积分布函数。因为这个函数没有解析解，所以要用近似函数来表示。

图像：

导数形式：

GELU和RELU一样，可以解决梯度消失，所以，GELU的优点就是在ReLU上增加随机因素，x越小越容易被mask掉。

==为什么用layernorm不用batchnorm？==

对于RNN来说，sequence的长度是不一致的，所以用很多padding来表示无意义的信息。如果BN会导致有意义的embedding损失信息。所以，BN一般用于CNN，而LN用于RNN。

layernorm是在hidden size的维度进行的，跟batch和seq_len无关。每个hidden state都计算自己的均值和方差，这是因为不同hidden state的量纲不一样。beta和gamma的维度都是(hidden_size,)，经过白化的hidden state * beta + gamma得到最后的结果。

LN在BERT中主要起到白化的作用，增强模型稳定性（如果删除则无法收敛）

==Multi-head Self-Attention==

如果是单头注意力，就是每个位置的embedding对应 三个向量，这三个向量分别是embedding点乘 矩阵得来的。每个位置的Q向量去乘上所有位置的K向量，其结果经过softmax变成attention score，以此作为权重对所有V向量做加权求和即可。

用公式表示为：

其中， 为 向量的hidden size。除以 叫做scaled dot product.

• 多头注意力是怎样的呢？

Transformer中先通过切头（spilt）再分别进行Scaled Dot-Product Attention。

step1：一个768维的hidden向量，被映射成Q，K，V。 然后三个向量分别切分成12(head_num)个小的64维的向量，每一组小向量之间做attention。不妨假设batch_size为32，seqlen为512，隐层维度为768，12个head。

hidden(32 x 512 x 768) -> Q(32 x 512 x 768) -> 32 x 12 x 512 x 64 hidden(32 x 512 x 768) -> K(32 x 512 x 768) -> 32 x 12 x 512 x 64 hidden(32 x 512 x 768) -> V(32 x 512 x 768) -> 32 x 12 x 512 x 64

step2：然后Q和K之间做attention，得到一个32 x 12 x 512 x 512的权重矩阵（时间复杂度O( ))，然后根据这个权重矩阵加权V中切分好的向量，得到一个32 x 12 x 512 x 64 的向量，拉平输出为768向量。

32 x 12 x 512 x 64(query_hidden) * 32 x 12 x 64 x 512(key_hidden) -> 32 x 12 x 512 x 512 32 x 12 x 64 x 512(value_hidden) * 32 x 12 x 512 x 512 (权重矩阵) -> 32 x 12 x 512 x 64

然后再还原成 -> 32 x 512 x 768 。简言之是12个头，每个头都是一个64维度，分别去与其他的所有位置的hidden embedding做attention然后再合并还原。

• 多头机制为什么有效？

类似于CNN中通过多通道机制进行特征选择。Transformer中使用切头(split)的方法，是为了在不增加复杂度（ )的前提下享受类似CNN中“不同卷积核”的优势。

==为什么要做scaled dot product?==

当输入信息的维度 d 比较高，会导致 softmax 函数接近饱和区，梯度会比较小。因此，缩放点积模型可以较好地解决这一问题。

==为什么用双线性点积模型（即Q，K两个向量）？==

双线性点积模型使用Q，K两个向量，而不是只用一个Q向量，这样引入非对称性，更具健壮性（Attention对角元素值不一定是最大的，也就是说当前位置对自身的注意力得分不一定最高）。

==Transformer的非线性来自于哪里？==

• FFN的gelu激活函数
• self-attention：注意self-attention是非线性的（因为有相乘和softmax）

李宏毅课程笔记：Adaptive Learning Rate

critical point其实不一定是,你在训练一个Network的时候,会遇到的最大的障碍,今天要告诉大家的是一个叫做Adaptive Learning Rate的技术,我们要给每一个参数不同的learning rate

一、Training stuck ≠ Small Gradient

People believe training stuck because the parameters are around a critical point …

人们认为，由于参数处于临界点附近，培训陷入困境;為什麼我说这个critical point不一定是我们训练过程中,最大的阻碍呢？

往往同学们,在训练一个network的时候,你会把它的loss记录下来,所以你会看到,你的loss原来很大,随著你参数不断的update,横轴代表参数update的次数,随著你参数不断的update,这个loss会越来越小,最后就卡住了,你的loss不再下降。

那多数这个时候,大家就会猜说,那是不是走到了critical point,因為gradient等於零的关係,所以我们没有办法再更新参数,但是真的是这样吗？

当我们说 走到critical point的时候,意味著gradient非常的小,但是你有确认过,当你的loss不再下降的时候,gradient真的很小吗？其实多数的同学可能,都没有确认过这件事,而事实上在这个例子裡面,在今天我show的这个例子裡面,当我们的loss不再下降的时候,gradient并没有真的变得很小

gradient是一个向量，下面是gradient的norm,即gradient这个向量的长度,随著参数更新的时候的变化,你会发现说虽然loss不再下降,但是这个gradient的norm,gradient的大小并没有真的变得很小

这样子的结果其实也不难猜想,也许你遇到的是这样子的状况

这个是我们的error surface,然后你现在的gradient,在error surface山谷的两个谷壁间,不断的来回的震荡

这个时候你的loss不会再下降,所以你会觉得它真的卡到了critical point,卡到了saddle point,卡到了local minima吗？不是的,它的gradient仍然很大,只是loss不见得再减小了

所以你要注意,当你今天训练一个network,train到后来发现,loss不再下降的时候,你不要随便说,我卡在local minima,我卡在saddle point,有时候根本两个都不是,你只是单纯的loss没有办法再下降

就是為什麼你在在作业2-2,会有一个作业叫大家,算一下gradient的norm,然后算一下说,你现在是卡在saddle point,还是critical point,因為多数的时候,当你说你训练卡住了,很少有人会去分析卡住的原因,為了强化你的印象,我们有一个作业,让你来分析一下,卡住的原因是什麼,

1.1 Wait a minute

有的同学就会有一个问题,如果我们在训练的时候,其实很少卡到saddle point,或者是local minima,那这一个图是怎麼做出来的呢?

我们上次有画过这个图是说我们现在训练一个Network,训练到现在参数在critical point附近,然后我们再来根据eigen value的正负号,来判断说这个critical point,比较像是saddle point,还是local minima

那如果实际上在训练的时候,要走到saddle point,或者是local minima,是一件困难的事情,那这个图到底是怎麼画出来的。那这边告诉大家一个秘密,这个图你要训练出这样子的结果,你要训练到你的参数很接近critical point,用一般的gradient descend,其实是做不到的,用一般的gradient descend train,你往往会得到的结果是,你在这个gradient还很大的时候,你的loss就已经掉了下去,这个是需要特别方法train的。

所以做完这个实验以后,我更感觉你要走到一个critical point,其实是困难的一件事,多数时候training,在还没有走到critical point的时候,就已经停止了,那这并不代表说,critical point不是一个问题,我只是想要告诉你说,我们真正目前,当你用gradient descend,来做optimization的时候,你真正应该要怪罪的对象,往往不是critical point,而是其他的原因。

1.2 Training can be difficult even without critical points

如果今天critical point不是问题的话,為什麼我们的training会卡住呢,我这边举一个非常简单的例子,我这边有一个,非常简单的error surface

我们只有两个参数,这两个参数值不一样的时候,Loss的值不一样,我们就画出了一个error surface,这个error surface的最低点在黄色X这个地方,事实上,这个error surface是convex的形状(可以理解为凸的或者凹的，convex optimization常翻译为“凸优化”)

如果你不知道convex是什麼,没有关係,总之它是一个,它的这个等高线是椭圆形的,只是它在横轴的地方,它的gradient非常的小,它的坡度的变化非常的小,非常的平滑,所以这个椭圆的长轴非常的长,短轴相对之下比较短,在纵轴的地方gradient的变化很大,error surface的坡度非常的陡峭

那现在我们要从黑点这个地方,这个地方当作初始的点,然后来做gradient descend，你可能觉得说,这个convex的error surface,做gradient descend,有什麼难的吗？不就是一路滑下来,然后可能再走过去吗,应该是非常容易。你实际上自己试一下,你会发现说,就连这种convex的error surface,形状这麼简单的error surface,你用gradient descend,都不见得能把它做好,举例来说这个是我实际上,自己试了一下的结果

我learning rate设10⁻²的时候,我的这个参数在峡谷的两端,我的参数在山壁的两端不断的震盪,我的loss掉不下去,但是gradient其实仍然是很大的。那你可能说,就是因為你learning rate设太大了阿,learning rate决定了我们update参数的时候步伐有多大,learning rate显然步伐太大,你没有办法慢慢地滑到山谷裡面只要把learning rate设小一点,不就可以解决这个问题了吗？

事实不然,因為我试著去,调整了这个learning rate,就会发现你光是要train这种convex的optimization的问题,你就觉得很痛苦,我就调这个learning rate,从10⁻²,一直调到10⁻⁷,调到10⁻⁷以后,终於不再震盪了

终於从这个地方滑滑滑,滑到山谷底终於左转,但是你发现说,这个训练永远走不到终点,因為我的learning rate已经太小了,竖直往上这一段这个很斜的地方,因為这个坡度很陡,gradient的值很大,所以还能够前进一点,左拐以后这个地方坡度已经非常的平滑了,这麼小的learning rate,根本没有办法再让我们的训练前进。

事实上在左拐这个地方,看到这边一大堆黑点,这边有十万个点,这个是张辽八百冲十万的那个十万,但是我都没有办法靠近,这个local minima的地方,所以显然就算是一个convex的error surface,你用gradient descend也很难train

这个convex的optimization的问题,确实有别的方法可以解,但是你想想看,如果今天是更复杂的error surface,你真的要train一个deep network的时候,gradient descend是你,唯一可以仰赖的工具,但是gradient descend这个工具,连这麼简单的error surface都做不好,一室之不治 何以天下国家為,这麼简单的问题都做不好,那如果难的问题,它又怎麼有可能做好呢

所以我们需要更好的gradient descend的版本,在之前我们的gradient descend裡面,所有的参数都是设同样的learning rate,这显然是不够的,learning rate它应该要為,每一个参数客製化,所以接下来我们就是要讲,客製化的learning rate,怎麼做到这件事情

二、Different parameters needs different learning rate

那我们要怎麼客製化learning rate呢,我们不同的参数到底,需要什麼样的learning rate呢？从刚才的例子裡面,其实我们可以看到一个大原则,如果在某一个方向上,我们的gradient的值很小,非常的平坦,那我们会希望learning rate调大一点,如果在某一个方向上非常的陡峭,坡度很大,那我们其实期待,learning rate可以设得小一点。

那这个learning rate要如何自动的,根据这个gradient的大小做调整呢？

我们要改一下,gradient descend原来的式子,我们只放某一个参数update的式子,我们之前在讲gradient descend,我们往往是讲,所有参数update的式子,那这边為了等一下简化这个问题,我们只看一个参数,但是你完全可以把这个方法,推广到所有参数的状况 \[ {θ{_i}{^{t+1}}} ← {θ{_i}{^{t}}}-{\eta}{g{_i}{^{t}}} \] 我们只看一个参数,这个参数叫做\({θ{_i}{^{t}}}\),这个\({θ{_i}{^{t}}}\)在第t个iteration的值,减掉在第t个iteration这个参数i算出来的gradient \({g{_i}{^{t}}}\) \[ {g{_i}{^{t}}}=\frac{\partial{L}}{\partial{θ_i}}|_{θ=θ^t} \] 这个\({g{_i}{^{t}}}\)代表在第t个iteration,也就是θ等於θᵗ的时候,参数θᵢ对loss的微分,我们把这个θᵢᵗ减掉learning rate,乘上gᵢᵗ会更新learning rate到θᵢᵗ⁺¹,这是我们原来的gradient descend,我们的learning rate是固定的

现在我们要有一个随著参数客製化的learning rate,我们把原来learning rate \(η\)这一项呢,改写成\(\frac{η}{σᵢᵗ}\) \[ {θ{_i}{^{t+1}}} ← {θ{_i}{^{t}}}-{\frac{η}{σᵢᵗ}}{g{_i}{^{t}}} \] 这个\(σᵢᵗ\)你发现它有一个上标t,有一个下标i,这代表说这个σ这个参数,首先它是depend on i的,不同的参数我们要给它不同的σ,同时它也是iteration dependent的,不同的iteration我们也会有不同的σ。

所以当我们把我们的learning rate,从η改成\(\frac{η}{σᵢᵗ}\)的时候,我们就有一个,parameter dependent的learning rate,接下来我们是要看说,这个parameter dependent的learning rate有什麼常见的计算方式。

2.1 Root mean square

那这个σ有什麼样的方式,可以把它计算出来呢,一个常见的类型是算,gradient的Root Mean Square（均方根）

现在参数要update的式子,我们从θᵢ⁰初始化参数减掉gᵢ⁰,乘上learning rate η除以σᵢ⁰,就得到θᵢ¹, \[ {θ{_i}{^{1}}} ← {θ{_i}{^{0}}}-{\frac{η}{σᵢ^0}}{g{_i}{^{0}}} \]

• 这个σᵢ⁰在第一次update参数的时候,这个σᵢ⁰是(gᵢ⁰)²开根号 \[ {σᵢ^0}=\sqrt{({g{_i}{^{0}}})^2}=|{g{_i}{^{0}}}| \] 这个gᵢ⁰就是我们的gradient,就是gradient的平方开根号,其实就是gᵢ⁰的绝对值,所以你把gᵢ⁰的绝对值代到\({θ{_i}{^{1}}} ← {θ{_i}{^{0}}}-{\frac{η}{σᵢ^0}}{g{_i}{^{0}}}\),这个式子中gᵢ⁰跟这个根号底下的gᵢ⁰,它们的大小是一样的,所以式子中这一项只会有一个,要嘛是正一 要嘛是负一,就代表说我们第一次在update参数,从θᵢ⁰update到θᵢ¹的时候,要嘛是加上η 要嘛是减掉η,跟这个gradient的大小没有关係,是看你η设多少,这个是第一步的状况

• 重点是接下来怎麼处理,那θᵢ¹它要一样,减掉gradient gᵢ¹乘上η除以σᵢ¹, \[ {θ{_i}{^{1}}}-{\frac{η}{σᵢ^1}}{g{_i}{^{1}}} \] 现在在第二次update参数的时候,是要除以σᵢ¹ ,这个σᵢ¹就是我们过去,所有计算出来的gradient,它的平方的平均再开根号 \[ {σᵢ^1}=\sqrt{\frac{1}{2}[{(g{_i}{^{0}}})^2+{(g{_i}{^{1}}})^2]} \] 我们到目前為止,在第一次update参数的时候,我们算出了gᵢ⁰,在第二次update参数的时候,我们算出了gᵢ¹,所以这个σᵢ¹就是(gᵢ⁰)²,加上(gᵢ¹)²除以½再开根号,这个就是Root Mean Square,我们算出这个σᵢ¹以后,我们的learning rate就是η除以σᵢ¹,然后把θᵢ¹减掉,η除以σᵢ¹乘以gᵢ¹ 得到θᵢ² \[ {θ{_i}{^{2}}} ← {θ{_i}{^{1}}}-{\frac{η}{σᵢ^1}}{g{_i}{^{1}}} \]

• 同样的操作就反覆继续下去,在θᵢ²的地方,你要减掉η除以σᵢ²乘以gᵢ², \[ {θ{_i}{^{2}}}-{\frac{η}{σᵢ^2}}{g{_i}{^{2}}} \] 那这个σ是什麼呢,这个σᵢ²就是过去,所有算出来的gradient,它的平方和的平均再开根号 \[ {σᵢ^2}=\sqrt{\frac{1}{3}[{(g{_i}{^{0}}})^2+{(g{_i}{^{1}}})^2+{(g{_i}{^{2}}})^2]} \] 所以你把gᵢ⁰取平方,gᵢ¹取平方 gᵢ²取平方,的平均再开根号,得到σᵢ²放在这个地方,然后update参数 \[ {θ{_i}{^{3}}} ← {θ{_i}{^{2}}}-{\frac{η}{σᵢ^2}}{g{_i}{^{2}}} \]

• 所以这个process这个过程,就反覆继续下去,到第t次update参数的时候,其实这个是第t + 1次,第t + 1次update参数的时候,你的这个σᵢᵗ它就是过去所有的gradient,gᵢᵗ从第一步到目前為止,所有算出来的gᵢᵗ的平方和,再平均 再开根号得到σᵢᵗ, \[ {σᵢ^t}=\sqrt{\frac{1}{t+1}\sum_{i=0}^{t}{(g{_i}{^{t}}})^2} \] 然后在把它除learning rate,然后用这一项当作是,新的learning rate来update你的参数, \[ {θ{_i}{^{t+1}}} ← {θ{_i}{^{t}}}-{\frac{η}{σᵢ^t}}{g{_i}{^{t}}} \]

2.2 Adagrad

那这一招被用在一个叫做Adagrad的方法裡面,為什麼这一招可以做到我们刚才讲的,坡度比较大的时候,learning rate就减小,坡度比较小的时候,learning rate就放大呢?

你可以想像说,现在我们有两个参数:一个叫θᵢ¹ 一个叫θᵢ² θᵢ¹坡度小 θᵢ²坡度大

• θᵢ¹因為它坡度小,所以你在θᵢ¹这个参数上面,算出来的gradient值都比较小
• 因為gradient算出来的值比较小,然后这个σ是gradient的平方和取平均再开根号

\[ {σᵢ^t}=\sqrt{\frac{1}{t+1}\sum_{i=0}^{t}{(g{_i}{^{t}}})^2} \]

• 所以算出来的σ就小,σ小 learning rate就大 \[ {\frac{η}{σᵢ^t}} \]

反过来说θᵢ²,θᵢ²是一个比较陡峭的参数,在θᵢ²这个方向上loss的变化比较大,所以算出来的gradient都比较大,,你的σ就比较大,你在update的时候 你的step,你的参数update的量就比较小

所以有了σ这一项以后,你就可以随著gradient的不同,每一个参数的gradient的不同,来自动的调整learning rate的大小,那这个并不是,你今天会用的最终极的版本,

2.3 RMSProp

刚才那个版本,就算是同一个参数,它需要的learning rate,也会随著时间而改变,我们刚才的假设,好像是同一个参数,它的gradient的大小,就会固定是差不多的值,但事实上并不一定是这个样子的。举例来说我们来看,这个新月形的error surface：

如果我们考虑横轴的话,考虑左右横的水平线的方向的话,你会发现说,在绿色箭头这个地方坡度比较陡峭,所以我们需要比较小的learning rate。

但是走到了中间这一段，到了红色箭头的时候呢,坡度又变得平滑了起来,平滑了起来就需要比较大的learning rate,所以就算是同一个参数同一个方向,我们也期待说,learning rate是可以动态的调整的,于是就有了一个新的招数,这个招数叫做RMS Prop。

RMS Prop这个方法,它的第一步跟刚才讲的Root Mean Square,也就是那个Apagrad的方法,是一模一样的 \[ {σᵢ^0}=\sqrt{({g_i^0})^2} \] 我们看第二步,一样要算出σᵢ¹,只是我们现在算出σᵢ¹的方法跟刚才,算Root Mean Square的时候不一样,刚才在算Root Mean Square的时候,每一个gradient都有同等的重要性,但在RMS Prop裡面,它决定你可以自己调整,现在的这个gradient,你觉得它有多重要 \[ {σᵢ^1}=\sqrt[]{\alpha(σ_i^0)^2+(1-\alpha)(g_i^1)^2} \] 所以在RMS Prop裡面,我们这个σᵢ¹它是前一步算出来的σᵢ⁰,裡面就是有gᵢ⁰,所以这个σᵢ⁰就代表了gᵢ⁰的大小,所以它是(σᵢ⁰)²,乘上α加上(1-α),乘上现在我们刚算出来的,新鲜热腾腾的gradient就是gᵢ¹

那这个α就像learning rate一样,这个你要自己调它,它是一个hyperparameter

• 如果我今天α设很小趋近於0,就代表我觉得gᵢ¹相较於之前所算出来的gradient而言,比较重要
• 我α设很大趋近於1,那就代表我觉得现在算出来的gᵢ¹比较不重要,之前算出来的gradient比较重要

所以同理在第三次update参数的时候,我们要算σᵢ² ,我们就把σᵢ¹拿出来取平方再乘上α,那σᵢ¹裡面有gᵢ¹跟σᵢ⁰ ,σᵢ⁰裡面又有gᵢ⁰,所以你知道σᵢ¹裡面它有gᵢ¹有gᵢ⁰, 然后这个gᵢ¹跟gᵢ⁰呢他们会被乘上α,然后再加上1-α乘上这个(gᵢ²)² \[ {σᵢ^2}=\sqrt[]{\alpha(σ_i^1)^2+(1-\alpha)(g_i^2)^2} \] 所以这个α就会决定说gᵢ²,它在整个σᵢ²裡面佔有多大的影响力

那同样的过程就反覆继续下去,σᵢᵗ等於根号α乘上(σᵢᵗ⁻¹)²,加上(1-α) (gᵢᵗ)², \[ {σᵢ^t}=\sqrt[]{\alpha(σ_i^{t-1})^2+(1-\alpha)(g_i^t)^2} \] 你用α来决定现在刚算出来的gᵢᵗ,它有多重要,好那这个就是RMSProp。那RMSProp我们刚刚讲过说,透过α这一项你可以决定说,gᵢᵗ相较於之前存在,σᵢᵗ⁻¹裡面的gᵢᵗ到gᵢᵗ⁻¹而言,它的重要性有多大,如果你用RMS Prop的话,你就可以动态调整σ这一项,我们现在假设从这个地方开始：

这个黑线是我们的error surface,从这个地方开始你要update参数,好你这个球就从这边走到这边,那因為一路上都很平坦,很平坦就代表说g算出来很小,代表现在update参数的时候,我们会走比较大的步伐

接下来继续滚,滚到这边以后我们gradient变大了,如果不是RMS Prop,原来的Adagrad的话它反应比较慢,但如果你用RMS Prop,然后呢你把α设小一点,你就是让新的,刚看到的gradient影响比较大的话,那你就可以很快的让σ的值变大,也可以很快的让你的步伐变小

你就可以踩一个煞车,本来很平滑走到这个地方,突然变得很陡,那RMS Prop可以很快的踩一个煞车,把learning rate变小,如果你没有踩剎车的话,你走到这裡这个地方,learning rate太大了,那gradient又很大,两个很大的东西乘起来,你可能就很快就飞出去了,飞到很远的地方

如果继续走,又走到平滑的地方了,因為这个σᵢᵗ 你可以调整α,让它比较看重於,最近算出来的gradient,所以你gradient一变小,σ可能就反应很快,它的这个值就变小了,然后呢你走的步伐就变大了,这个就是RMS Prop,

2.4 Adam

那今天你最常用的,optimization的策略,有人又叫做optimizer,今天最常用的optimization的策略,就是Adam

Adam就是RMS Prop加上Momentum,那Adam的演算法跟原始的论文https://arxiv.org/pdf/1412.6980.pdf

今天pytorch裡面,都帮你写得好好的了,所以这个你今天,不用担心这种optimization的问题,optimizer这个deep learning的套件,往往都帮你做好了,然后这个optimizer裡面,也有一些参数需要调,也有一些hyperparameter,需要人工决定,但是你往往用预设的,那一种参数就够好了,你自己调有时候会调到比较差的,往往你直接copy,这个pytorch裡面,Adam这个optimizer,然后预设的参数不要随便调,就可以得到不错的结果了,关於Adam的细节,就留给大家自己研究

三、Learning Rate Scheduling

我们刚才讲说这个简单的error surface,我们都train不起来,现在我们来看一下,加上Adaptive Learning Rate以后,train不train得起来。

那这边是採用,最原始的Adagrad那个做法啦,就是把过去看过的,这个learning rate通通都,过去看过的gradient,通通都取平方再平均再开根号当作这个σ ,做起来是这个样子的

这个走下来没有问题,然后接下来在左转的时候,这边也是update了十万次,之前update了十万次,只卡在左转这个地方

那现在有Adagrad以后,你可以再继续走下去,走到非常接近终点的位置,因為当你走到这个地方的时候,你因為这个左右的方向的,这个gradient很小,所以learning rate会自动调整,左右这个方向的,learning rate会自动变大,所以你这个步伐就可以变大,就可以不断的前进

接下来的问题就是,為什麼快走到终点的时候突然爆炸了呢？你想想看 我们在做这个σ的时候,我们是把过去所有看到的gradient,都拿来作平均

• 所以这个纵轴的方向,在这个初始的这个地方,感觉gradient很大

• 可是这边走了很长一段路以后,这个纵轴的方向,gradient算出来都很小,所以纵轴这个方向,这个y轴的方向就累积了很小的σ

• 因為我们在这个y轴的方向,看到很多很小的gradient,所以我们就累积了很小的σ,累积到一个地步以后,这个step就变很大,然后就爆走就喷出去了

• 喷出去以后没关係,有办法修正回来,因為喷出去以后,就走到了这个gradient比较大的地方,走到gradient比较大的地方以后,这个σ又慢慢的变大,σ慢慢变大以后,这个参数update的距离,Update的步伐大小就慢慢的变小

你就发现说走著走著,突然往左右喷了一下,但是这个喷了一下不会永远就是震盪,不会做简谐运动停不下来,这个力道慢慢变小,有摩擦力 让它慢慢地慢慢地,又回到中间这个峡谷来,然后但是又累计一段时间以后 又会喷,然后又慢慢地回来 怎麼办呢,有一个方法也许可以解决这个问题,这个叫做learning rate的scheduling

什麼是learning rate的scheduling呢？

我们刚才这边还有一项η,这个η是一个固定的值,learning rate scheduling的意思就是说,我们不要把η当一个常数,我们把它跟时间有关

最常见的策略叫做Learning Rate Decay,也就是说，随著时间的不断地进行,随著参数不断的update,我们这个η让它越来越小。

那这个也就合理了,因為一开始我们距离终点很远,随著参数不断update,我们距离终点越来越近,所以我们把learning rate减小,让我们参数的更新踩了一个煞车,让我们参数的更新能够慢慢地慢下来,所以刚才那个状况,如果加上Learning Rate Decay有办法解决。

刚才那个状况,如果加上Learning Rate Decay的话,我们就可以很平顺的走到终点,因為在这个地方,这个η已经变得非常的小了,虽然说它本来想要左右乱喷,但是因為乘上这个非常小的η,就停下来了 就可以慢慢地走到终点,那除了Learning Rate Decay以外,还有另外一个经典，常用的Learning Rate Scheduling的方式,叫做Warm Up

Warm Up这个方法,听起来有点匪夷所思,这Warm Up的方法是让learning rate,要先变大后变小,你会问说 变大要变到多大呢,变大速度要多快呢 ，小速度要多快呢,这个也是hyperparameter,你要自己用手调的,但是大方向的大策略就是,learning rate要先变大后变小,那这个方法听起来很神奇,就是一个黑科技这样,这个黑科技出现在,很多远古时代的论文裡面。

这个warm up,最近因為在训练BERT的时候,往往需要用到Warm Up,所以又被大家常常拿出来讲,但它并不是有BERT以后,才有Warm Up的,Warm Up这东西远古时代就有了,举例来说,Residual Network裡面是有Warm Up的

这边是放了Residual network,放在arXiv上面的文章连结啦,今天这种有关machine learning 的,文章往往在投conference之前,投国际会议之前,就先放到一个叫做arXiv的网站上,把它公开来让全世界的人都可以看。

你其实看这个arXiv的网址,你就可以知道,这篇文章是什麼时候放到网路上的,怎麼看呢 arXiv的前四个数字,这15代表年份,代表说residual network这篇文章,是2015年放到arXiv上面的,后两个数字代表月份,所以它是15年的12月,15年的年底放在arXiv上面的

所以五六年前的文章,在deep learning变化,这麼快速的领域裡面,五六年前就是上古时代,那在上古时代,这个Residual Network裡面,就已经记载了Warm Up的这件事情,它说我们用learning rate 0.01,取Warm Up,先用learning rate 0.01,再把learning rate改成0.1

用过去我们通常最常见的train,Learning Rate Scheduling的方法,就是让learning rate越来越小,但是Residual Network,这边特别註明它反其道而行,一开始要设0.01 接下来设0.1,还特别加一个註解说,一开始就用0.1反而就train不好,不知道為什麼 也没解释,反正就是train不好,需要Warm Up这个黑科技。而在这个黑科技,在知名的Transformer裡面(这门课也会讲到),也用一个式子提了它。

它这边有一个式子说,它的learning rate遵守这一个,神奇的function来设定,它的learning rate,这个神奇的function,乍看之下会觉得 哇 在写什麼,不知道在写些什麼。这个东西你实际上,把这个function画出来,你实际上把equation画出来的话,就会发现它就是Warm Up,learning rate会先增加,然后接下来再递减。所以你发现说Warm Up这个技术,在很多知名的network裡面都有,被当作一个黑科技,就论文裡面不解释说,為什麼要用这个,但就偷偷在一个小地方,你没有注意到的小地方告诉你说,这个network要用这种黑科技,才能够把它训练起来。那為什麼需要warm Up呢,这个仍然是今天,一个可以研究的问题啦。

这边有一个可能的解释是说,你想想看当我们在用Adam RMS Prop,或Adagrad的时候,我们会需要计算σ,它是一个统计的结果,σ告诉我们,某一个方向它到底有多陡,或者是多平滑,那这个统计的结果,要看得够多笔数据以后,这个统计才精準,所以一开始我们的统计是不精準的

一开始我们的σ是不精準的,所以我们一开始不要让我们的参数,走离初始的地方太远,先让它在初始的地方呢,做一些像是探索这样,所以一开始learning rate比较小,是让它探索 收集一些有关error surface的情报,先收集有关σ的统计数据,等σ统计得比较精準以后,在让learning rate呢慢慢地爬升

所以这是一个解释,為什麼我们需要warm up的可能性,那如果你想要学更多,有关warm up的东西的话,你其实可以看一篇paper,它是Adam的进阶版叫做RAdam,裡面对warm up这件事情,有更多的理解。

四、Summary of Optimization

所以我们从最原始的gradient descent,进化到这一个版本：

这个版本裡面

• 我们有Momentum,也就是说我们现在,不是完全顺著gradient的方向,现在不是完全顺著这一个时间点,算出来的gradient的方向,来update参数,而是把过去,所有算出来gradient的方向,做一个加总当作update的方向,这个是momentum

• 接下来应该要update多大的步伐呢,我们要除掉,gradient的Root Mean Square

  

  那讲到这边可能有同学会觉得很困惑,这一个momentum是考虑,过去所有的gradient,这个σ也是考虑过去所有的gradient,一个放在分子一个放在分母,都考虑过去所有的gradient,不就是正好抵销了吗？,

  但是其实这个Momentum跟这个σ,它们在使用过去所有gradient的方式是不一样的：

  • Momentum是直接把所有的gradient通通都加起来,所以它有考虑方向,它有考虑gradient的正负号,它有考虑gradient是往左走还是往右走。

  • Root Mean Square,它就不考虑gradient的方向了。它只考虑gradient的大小,记不记得我们在算σ的时候,我们都要取平方项,我们都要把gradient取一个平方项,我们是把平方的结果加起来,所以我们只考虑gradient的大小,不考虑它的方向,所以Momentum跟这个σ,算出来的结果并不会互相抵销掉。

• 那最后我们还会加上,一个learning rate的scheduling：

  

  那这个是今天optimization的,完整的版本了,这种Optimizer,除了Adam以外,Adam可能是今天最常用的,但除了Adam以外,还有各式各样的变形,但其实各式各样的变形都不脱,就是要嘛不同的方法算M,要嘛不同的方法算σ,要嘛不同的,Learning Rate Scheduling的方式。

一、李宏毅课程笔记：Batch and Momentum

1.1 Review： Optimization with Batch

上次我们有讲说,我们实际上在算微分的时候,并不是真的对所有 Data 算出来的 L 作微分,你是把所有的 Data 分成一个一个的 Batch,有的人是叫Mini Batch ,那我这边叫做 Batch,其实指的是一样的东西,助教投影片里面,是写 Mini Batch。

每一个 Batch 的大小呢,就是大 B 一笔的资料,我们每次在 Update 参数的时候,我们是拿大 B 一笔资料出来,算个 Loss,算个 Gradient,Update 参数,拿另外B一笔资料,再算个 Loss,再算个 Gradient,再 Update 参数,以此类推,所以我们不会拿所有的资料一起去算出 Loss,我们只会拿一个 Batch 的资料,拿出来算 Loss。

所有的 Batch 看过一遍,叫做一个 Epoch,那事实上啊,你今天在做这些 Batch 的时候,你会做一件事情叫做 Shuffle

Shuffle 有很多不同的做法,但一个常见的做法就是, 在每一个 Epoch 开始之前,会分一次 Batch,然后呢,每一个 Epoch 的 Batch 都不一样,就是第一个 Epoch,我们分这样子的 Batch,第二个 Epoch,会重新再分一次 Batch,所以哪些资料在同一个 Batch 里面,每一个 Epoch 都不一样的这件事情,叫做 Shuffle。

1.2 Small Batch v.s. Large Batch

​ 我们先解释为什么要用 Batch,再说 Batch 对 Training 带来了什么样的帮助。

我们来比较左右两边这两个 Case,那假设现在我们有20笔训练资料

• 左边的 Case 就是没有用 Batch,Batch Size,直接设的跟我训练资料一样多,这种状况叫做 Full Batch,就是没有用 Batch 的意思
• 那右边的 Case 就是,Batch Size 等於1

​ 这是两个最极端的状况

我们先来看左边的 Case,在左边 Case 里面,因为没有用 Batch,我们的 Model 必须把20笔训练资料都看完,才能够计算 Loss,才能够计算 Gradient,所以我们必须要把所有20笔 Example s 都看完以后,我们的参数才能够 Update 一次。就假设开始的地方在上边边,把所有资料都看完以后,Update 参数就从这里移动到下边。

如果 Batch Size 等於1的话,代表我们只需要拿一笔资料出来算 Loss,我们就可以 Update 我们的参数,所以每次我们 Update 参数的时候,看一笔资料就好,所以我们开始的点在这边,看一笔资料 就 Update 一次参数,再看一笔资料 就 Update 一次参数,如果今天总共有20笔资料的话 那在每一个 Epoch 里面,我们的参数会 Update 20次,那不过,因为我们现在是只看一笔资料,就 Update 一次参数,所以用一笔资料算出来的 Loss,显然是比较 Noisy 的,所以我们今天 Update 的方向,你会发现它是曲曲折折的

所以如果我们比较左边跟右边，哪一个比较好呢,他们有什么差别呢？

你会发现左边没有用 Batch 的方式,它蓄力的时间比较长,还有它技能冷却的时间比较长,你要把所有的资料都看过一遍,才能够 Update 一次参数

而右边的这个方法,Batch Size 等於1的时候,蓄力的时间比较短,每次看到一笔参数,每次看到一笔资料,你就会更新一次你的参数

所以今天假设有20笔资料,看完所有资料看过一遍,你已经更新了20次的参数,但是左边这样子的方法有一个优点,就是它这一步走的是稳的,那右边这个方法它的缺点,就是它每一步走的是不稳的

看起来左边的方法跟右边的方法,他们各自都有擅长跟不擅长的东西,左边是蓄力时间长,但是威力比较大,右边技能冷却时间短,但是它是比较不準的,看起来各自有各自的优缺点,但是你会觉得说,左边的方法技能冷却时间长,右边的方法技能冷却时间短,那只是你没有考虑并行运算的问题。

实际上考虑并行运算的话,左边这个并不一定时间比较长

1.3 Larger batch size does not require longer time to compute gradient

这边是真正的实验结果了,事实上,比较大的 Batch Size,你要算 Loss,再进而算 Gradient,所需要的时间,不一定比小的 Batch Size 要花的时间长。

那以下是做在一个叫做 MNIST 上面,MNIST (Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库,机器要做的事情,就是给它一张图片,然后判断这张图片,是0到9的哪一个数字,它要做数字的分类,那 MNIST 呢 是机器学习的helloworld,就是假设你今天,从来没有做过机器学习的任务,一般大家第一个会尝试的机器学习的任务,往往就是做 MNIST 做手写数字辨识,

这边我们就是做了一个实验,我们想要知道说,给机器一个 Batch,它要计算出 Gradient,进而 Update 参数,到底需要花多少的时间

这边列出了 Batch Size 等於1 等於10,等於100 等於1000 所需要耗费的时间

你会发现说 Batch Size 从1到1000,需要耗费的时间几乎是一样的,你可能直觉上认为有1000笔资料,那需要计算 Loss,然后计算 Gradient,花的时间不会是一笔资料的1000倍吗,但是实际上并不是这样的

因为在实际上做运算的时候,我们有 GPU,可以做并行运算,是因为你可以做平行运算的关係,这1000笔资料是平行处理的,所以1000笔资料所花的时间,并不是一笔资料的1000倍。当然 GPU 平行运算的能力还是有它的极限,当你的 Batch Size 真的非常非常巨大的时候,GPU 在跑完一个 Batch,计算出 Gradient 所花费的时间,还是会随著 Batch Size 的增加,而逐渐增长

所以今天如果 Batch Size 是从1到1000,所需要的时间几乎是一样的,但是当你的 Batch Size 增加到 10000,乃至增加到60000的时候,你就会发现 GPU 要算完一个 Batch,把这个 Batch 里面的资料都拿出来算 Loss,再进而算 Gradient,所要耗费的时间,确实有随著 Batch Size 的增加而逐渐增长,但你会发现这边用的是 V100,所以它挺厉害的,给它60000笔资料,一个 Batch 里面,塞了60000笔资料,它在10秒鐘之内,也是把 Gradient 就算出来

而那这个 Batch Size 的大小跟时间的关係,其实每年都会做这个实验,我特别把旧的投影片放在这边了,如果你有兴趣的话m,,可以看到这个时代的演进这样,17年的时候用的是那个980啊,2015年的时候用的是那个760啊,然后980要跑什么60000个 Batch,那要跑好几分鐘才跑得完啊,现在只要10秒鐘就可以跑得完了,你可以看到这个时代的演进,

1.4 Smaller batch requires longer time for one epoch

所以 GPU 虽然有平行运算的能力,但它平行运算能力终究是有个极限,所以你 Batch Size 真的很大的时候,时间还是会增加的

但是因为有平行运算的能力,因此实际上,当你的 Batch Size 小的时候,你要跑完一个 Epoch,花的时间是比大的 Batch Size 还要多的,怎么说呢

如果今天假设我们的训练资料只有60000笔,那 Batch Size 设1,那你要60000个 Update 才能跑完一个 Epoch,如果今天是 Batch Size 等於1000,你要60个 Update 才能跑完一个 Epoch,假设今天一个 Batch Size 等於1000,要算 Gradient 的时间根本差不多,那60000次 Update,跟60次 Update 比起来,它的时间的差距量就非常可观了

所以左边这个图是 Update 一次参数,拿一个 Batch 出来计算一个 Gradient,Update 一次参数所需要的时间,右边这个图是,跑完一个完整的 Epoch,需要花的时间,你会发现左边的图跟右边的图,它的趋势正好是相反的,假设你 Batch Size 这个1,跑完一个 Epoch,你要 Update 60000次参数,它的时间是非常可观的,但是假设你的 Batch Size 是1000,你只要跑60次,Update 60次参数就会跑完一个 Epoch,所以你跑完一个 Epoch,看完所有资料的时间,如果你的 Batch Size 设1000,其实是比较短的,Batch Size 设1000的时候,把所有的资料看过一遍,其实是比 Batch Size 设1 还要更快

所以如果我们看右边这个图的话,看完一个 Batch,把所有的资料看过一次这件事情,大的 Batch Size 反而是较有效率的,是不是跟你直觉想的不太一样

在没有考虑平行运算的时候,你觉得大的 Batch 比较慢,但实际上,在有考虑平行运算的时候,一个 Epoch 大的 Batch 花的时间反而是比较少的

我们如果要比较这个 Batch Size 大小的差异的话,看起来直接用技能时间冷却的长短,并不是一个精确的描述,看起来在技能时间上面,大的 Batch 并没有比较吃亏,甚至还佔到优势了.

所以事实上,20笔资料 Update 一次的时间,跟右边看一笔资料 Update 一次的时间,如果你用 GPU 的话,其实可能根本就是所以一样的,所以大的 Batch,它的技能时间,它技能冷却的时间,并没有比较长,那所以这时候你可能就会说,欸 那个大的 Batch 的劣势消失了,那难道它真的就,那这样看起来大的 Batch 应该比较好?

你不是说大的 Batch,这个 Update 比较稳定,小的 Batch,它的 Gradient 的方向比较 Noisy 吗,那这样看起来,大的 Batch 好像应该比较好哦,小的 Batch 应该比较差,因为现在大的 Batch 的劣势已经,因为平行运算的时间被拿掉了,它好像只剩下优势而已.

那神奇的地方是 Noisy 的 Gradient,反而可以帮助 Training,这个也是跟直觉正好相反的

如果你今天拿不同的 Batch 来训练你的模型,你可能会得到这样子的结果,左边是坐在 MNIST 上,右边是坐在 CIFAR-10 上,不管是 MNIST 还是 CIFAR-10,都是影像辨识的问题

• 横轴代表的是 Batch Size,从左到右越来越大
• 纵轴代表的是正确率,越上面正确率越高,当然正确率越高越好

而如果你今天看 Validation Acc 上的结果，会发现说,Batch Size 越大,Validation Acc 上的结果越差,但这个不是 Overfitting,因为如果你看你的 Training 的话,会发现说 Batch Size 越大,Training 的结果也是越差的,而我们现在用的是同一个模型哦,照理说,它们可以表示的 Function 就是一模一样的

但是神奇的事情是,大的 Batch Size,往往在 Training 的时候,会给你带来比较差的结果

所以这个是什么样的问题,同样的 Model,所以这个不是 Model Bias 的问题,这个是 Optimization 的问题,代表当你用大的 Batch Size 的时候,你的 Optimization 可能会有问题,小的 Batch Size,Optimization 的结果反而是比较好的,好 为什么会这样子呢

1,5 “Noisy” update is better for training

为什么小的 Batch Size,在 Training Set 上会得到比较好的结果,为什么 Noisy 的 Update,Noisy 的 Gradient 会在 Training 的时候,给我们比较好的结果呢？一个可能的解释是这样子的

假设你是 Full Batch,那你今天在 Update 你的参数的时候,你就是沿著一个 Loss Function 来 Update 参数,今天 Update 参数的时候走到一个 Local Minima,走到一个 Saddle Point,显然就停下来了,Gradient 是零,如果你不特别去看Hession的话,那你用 Gradient Descent 的方法,你就没有办法再更新你的参数了

但是假如是 Small Batch 的话,因为我们每次是挑一个 Batch 出来,算它的 Loss,所以等於是,等於你每一次 Update 你的参数的时候,你用的 Loss Function 都是越有差异的,你选到第一个 Batch 的时候,你是用 L1 来算你的 Gradient,你选到第二个 Batch 的时候,你是用 L2 来算你的 Gradient,假设你用 L1 算 Gradient 的时候,发现 Gradient 是零,卡住了,但 L2 它的 Function 跟 L1 又不一样,L2 就不一定会卡住,所以 L1 卡住了 没关係,换下一个 Batch 来,L2 再算 Gradient。

你还是有办法 Training 你的 Model,还是有办法让你的 Loss 变小,所以今天这种 Noisy 的 Update 的方式,结果反而对 Training,其实是有帮助的。

1.6 “Noisy” update is better for generalization

那这边还有另外一个更神奇的事情，其实小的 Batch 也对 Testing 有帮助。

假设我们今天在 Training 的时候,都不管是大的 Batch 还小的 Batch,都 Training 到一样好,刚才的 Case是Training 的时候就已经 Training 不好了。

假设你有一些方法,你努力的调大的 Batch 的 Learning Rate,然后想办法把大的 Batch,跟小的 Batch Training 得一样好,结果你会发现小的 Batch,居然在 Testing 的时候会是比较好的,那以下这个实验结果是引用自,On Large-Batch Training For Deep Learning,Generalization Gap And Sharp Minimahttps://arxiv.org/abs/1609.04836,这篇 Paper 的实验结果：

那这篇 Paper 里面,作者 Train 了六个 Network 里面有 CNN 的,有 Fully Connected Network 的,做在不同的 Cover 上,来代表这个实验是很泛用的,在很多不同的 Case 都观察到一样的结果,那它有小的 Batch,一个 Batch 里面有256笔 Example,大的 Batch 就是那个 Data Set 乘 0.1,Data Set 乘 0.1,Data Set 有60000笔,那你就是一个 Batch 里面有6000笔资料

然后他想办法,在大的 Batch 跟小的 Batch,都 Train 到差不多的 Training 的 Accuracy,所以刚才我们看到的结果是,Batch Size 大的时候,Training Accuracy 就已经差掉了,这边不是想办法 Train 到大的 Batch 的时候,Training Accuracy 跟小的 Batch,其实是差不多的

但是就算是在 Training 的时候结果差不多,Testing 的时候你还是看到了,小的 Batch 居然比大的 Batch 差,Training 的时候都很好,Testing 的时候大的 Batch 差,代表 Over Fitting,这个才是 Over Fitting 对不对,好 那为什么会有这样子的现象呢？在这篇文章里面也给出了一个解释,

假设这个是我们的 Training Loss,那在这个 Training Loss 上面呢,可能有很多个 Local Minima,有不只一个 Local Minima,那这些 Local Minima 它们的 Loss 都很低,它们 Loss 可能都趋近於 0,但是这个 Local Minima,还是有好 Minima 跟坏 Minima 之分

如果一个 Local Minima 它在一个峡谷里面,它是坏的 Minima,然后它在一个平原上,它是好的 Minima,为什么会有这样的差异呢

• 因为假设现在 Training 跟 Testing 中间,有一个 Mismatch,Training 的 Loss 跟 Testing 的 Loss,它们那个 Function 不一样,有可能是本来你 Training 跟 Testing 的 Distribution就不一样。
• 那也有可能是因为 Training 跟 Testing,你都是从 Sample 的 Data 算出来的,也许 Training 跟 Testing,Sample 到的 Data 不一样,那所以它们算出来的 Loss,当然是有一点差距。

那我们就假设说这个 Training 跟 Testing,它的差距就是把 Training 的 Loss,这个 Function 往右平移一点,这时候你会发现,对左边这个在一个盆地里面的 Minima 来说,它的在 Training 跟 Testing 上面的结果,不会差太多,只差了一点点,但是对右边这个在峡谷里面的 Minima 来说,一差就可以天差地远

它在这个 Training Set 上,算出来的 Loss 很低,但是因为 Training 跟 Testing 之间的不一样,所以 Testing 的时候,这个 Error Surface 一变,它算出来的 Loss 就变得很大,而很多人相信这个大的 Batch Size,会让我们倾向於走到峡谷里面,而小的 Batch Size,倾向於让我们走到盆地里面

那他直觉上的想法是这样,就是小的 Batch,它有很多的 Loss,它每次 Update 的方向都不太一样,所以如果今天这个峡谷非常地窄,它可能一个不小心就跳出去了,因为每次 Update 的方向都不太一样,它的 Update 的方向也就随机性,所以一个很小的峡谷,没有办法困住小的 Batch

如果峡谷很小,它可能动一下就跳出去,之后停下来如果有一个非常宽的盆地,它才会停下来,那对於大的 Batch Size,反正它就是顺著规定 Update,然后它就很有可能,走到一个比较小的峡谷里面

但这只是一个解释,那也不是每个人都相信这个解释,那这个其实还是一个尚待研究的问题那这边就是比较了一下,大的 Batch 跟小的 Batch

左边这个是第一个 Column 是小的 Batch,第二个 Column 是大的 Batch

在有平行运算的情况下,小的 Batch 跟大的 Batch,其实运算的时间并没有太大的差距,除非你的大的 Batch 那个大是真的非常大,才会显示出差距来。但是一个 Epoch 需要的时间,小的 Batch 比较长,大的 Batch 反而是比较快的,所以从一个 Epoch 需要的时间来看,大的 Batch 其实是佔到优势的。

而小的 Batch,你会 Update 的方向比较 Noisy,大的 Batch Update 的方向比较稳定,但是 Noisy 的 Update 的方向,反而在 Optimization 的时候会佔到优势,而且在 Testing 的时候也会佔到优势,所以大的 Batch 跟小的 Batch,它们各自有它们擅长的地方。

所以 Batch Size,变成另外一个 你需要去调整的 Hyperparameter。

那我们能不能够鱼与熊掌兼得呢,我们能不能够截取大的 Batch 的优点,跟小的 Batch 的优点,我们用大的 Batch Size 来做训练,用平行运算的能力来增加训练的效率,但是训练出来的结果同时又得到好的结果呢,又得到好的训练结果呢。

这是有可能的,有很多文章都在探讨这个问题,那今天我们就不细讲,我们把这些 Reference 列在这边给大家参考,那你发现这些 Paper,往往它想要做的事情都是什么,哇 76分鐘 Train BERT,15分鐘 Train ResNet,一分鐘 Train Imagenet 等等,这为什么他们可以做到那么快,就是因为他们 Batch Size 是真的开很大,比如说在第一篇 Paper 里面,Batch Size 里面有三万笔 Example 这样,Batch Size 开很大,Batch Size 开大 真的就可以算很快,你可以在很短的时间内看到大量的资料,那他们需要有一些特别的方法来解决,Batch Size 可能会带来的劣势。

二、Momentum

Momentum,这也是另外一个,有可能可以对抗 Saddle Point,或 Local Minima 的技术,Momentum 的运作是这个样子的，

2.1 Small Gradient

它的概念,你可以想像成在物理的世界里面,假设 Error Surface 就是真正的斜坡,而我们的参数是一个球,你把球从斜坡上滚下来,如果今天是 Gradient Descent,它走到 Local Minima 就停住了,走到 Saddle Point 就停住了

但是在物理的世界里,一个球如果从高处滚下来,从高处滚下来就算滚到 Saddle Point,如果有惯性,它从左边滚下来,因为惯性的关係它还是会继续往右走,甚至它走到一个 Local Minima,如果今天它的动量够大的话,它还是会继续往右走,甚至翻过这个小坡然后继续往右走

那所以今天在物理的世界里面,一个球从高处滚下来的时候,它并不会被 Saddle Point,或 Local Minima卡住,不一定会被 Saddle Point,或 Local Minima 卡住,我们有没有办法运用这样子的概念,到 Gradient Descent 里面呢,那这个就是我们等一下要讲的,Momentum 这个技术

2.2 Vanilla Gradient Descent

那我们先很快的复习一下,原来的 Gradient Descent 长得是什么样子,这个是 Vanilla 的 Gradient Descent,Vanilla 的意思就是一般的的意思,它直译是香草的,但就其实是一般的,一般的 Gradient Descent 长什么样子呢？

​

一般的 Gradient Descent 是说,我们有一个初始的参数叫做 \(θ^0\),我们计算一下 Gradient,然后计算完这个 Gradient 以后呢,我们往 Gradient 的反方向去 Update 参数 \[ θ^1 = θ^0 - {\eta}g^0 \] 我们到了新的参数以后,再计算一次 Gradient,再往 Gradient 的反方向,再 Update 一次参数,到了新的位置以后再计算一次 Gradient,再往 Gradient 的反方向去 Update 参数,这个 Process 就一直这样子下去

2.3 Gradient Descent + Momentum

加上 Momentum 以后,每一次我们在移动我们的参数的时候,我们不是只往 Gradient Descent,我们不是只往 Gradient 的反方向来移动参数,我们是 Gradient 的反方向,加上前一步移动的方向,两者加起来的结果,去调整去到我们的参数,

那具体说起来是这个样子,一样找一个初始的参数,然后我们假设前一步的参数的 Update 量呢,就设为 0 \[ m^0 = 0 \] 接下来在 \(θ^0\) 的地方,计算 Gradient 的方向\(g^0\)，然后接下来你要决定下一步要怎么走,它是 Gradient 的方向加上前一步的方向,不过因为前一步正好是 0,现在是刚初始的时候所以前一步是 0,所以 Update 的方向,跟原来的 Gradient Descent 是一样的,这没有什么有趣的地方

\[ m^1 = {\lambda}m^0-{\eta}g^0\\\ θ^1 = θ^0 + m^1 \] 但从第二步开始,有加上 Momentum 以后就不太一样了,从第二步开始,我们计算 \(g^1\),然后接下来我们 Update 的方向,不是 \(g^1\)的反方向,而是根据上一次 Update 方向,也就是 m1 减掉 g1,当做我们新的 Update 的方向,这边写成 m2 \[ m^2 = {\lambda}m^1-{\eta}g^1 \] 那我们就看下面这个图

g1 告诉我们,Gradient 告诉我们要往红色反方向这边走,但是我们不是只听 Gradient 的话,加上 Momentum 以后,我们不是只根据 Gradient 的反方向,来调整我们的参数,我们也会看前一次 Update 的方向

• 如果前一次说要往\(m^1\)蓝色及蓝色虚线这个方向走
• Gradient 说要往红色反方向这个方向走
• 把两者相加起来,走两者的折中,也就是往蓝色\(m^2\)这一个方向走,所以我们就移动了 m2,走到 θ2 这个地方

接下来就反覆进行同样的过程,在这个位置我们计算出 Gradient,但我们不是只根据 Gradient 反方向走,我们看前一步怎么走,前一步走这个方向,走这个蓝色虚线的方向,我们把蓝色的虚线加红色的虚线,前一步指示的方向跟 Gradient 指示的方向,当做我们下一步要移动的方向

每一步的移动,我们都用 m 来表示,那这个 m 其实可以写成之前所有算出来的,Gradient 的 Weighted Sum.从右边的这个式子,其实就可以轻易的看出来 \[ m^0 = 0\\\ m^1 = -{\eta}g^0\\\ m^2 = -{\lambda}{\eta}g^0-{\eta}g^1\\\ ... \] m0 我们把它设为 0,m1 是 m0 减掉 g0,m0 为 0,所以 m1 就是 g0 乘上负的 η,m2 是 λ 乘上 m1,λ 就是另外一个参数,就好像 η 是 Learning Rate 我们要调,λ 是另外一个参数,这个也是需要调的,m2 等於 λ 乘上 m1,减掉 η 乘上 g1,然后 m1 在哪里呢,m1 在这边,你把 m1 代进来,就知道说 m2,等於负的 λ 乘上 η 乘以 g0,减掉 η 乘上 g1,它是 g0 跟 g1 的 Weighted Sum

以此类推,所以你会发现说,现在这个加上 Momentum 以后,一个解读是 Momentum 是,Gradient 的负反方向加上前一次移动的方向,那但另外一个解读方式是,所谓的 Momentum,当加上 Momentum 的时候,我们 Update 的方向,不是只考虑现在的 Gradient,而是考虑过去所有 Gradient 的总合.

​ 有一个更简单的例子,希望帮助你了解 Momentum

那我们从这个地方开始 Update 参数,根据 Gradient 的方向告诉我们,应该往右 Update 参数,那现在没有前一次 Update 的方向,所以我们就完全按照 Gradient 给我们的指示,往右移动参数,好 那我们的参数,就往右移动了一点到这个地方

Gradient 变得很小,告诉我们往右移动,但是只有往右移动一点点,但前一步是往右移动的,我们把前一步的方向用虚线来表示,放在这个地方,我们把之前 Gradient 告诉我们要走的方向,跟前一步移动的方向加起来,得到往右走的方向,那再往右走 走到一个 Local Minima,照理说走到 Local Minima,一般 Gradient Descent 就无法向前走了,因为已经没有这个 Gradient 的方向,那走到 Saddle Point 也一样,没有 Gradient 的方向已经无法向前走了

但没有关係,如果有 Momentum 的话,你还是有办法继续走下去,因为 Momentum 不是只看 Gradient,Gradient 就算是 0,你还有前一步的方向,前一步的方向告诉我们向右走,我们就继续向右走,甚至你走到这种地方,Gradient 告诉你应该要往左走了,但是假设你前一步的影响力,比 Gradient 要大的话,你还是有可能继续往右走,甚至翻过一个小丘,搞不好就可以走到更好 Local Minima,这个就是 Momentum 有可能带来的好处。

Concluding Remarks

• Critical points have zero gradients.
• Critical points can be either saddle points or local minima.
  • Can be determined by the Hessian matrix.
  • Local minima may be rare.
  • It is possible to escape saddle points along the direction of eigenvectors of the Hessian matrix
• Smaller batch size and momentum help escape critical points.

参考文献

• python+numpy实现线性回归中梯度下降算法（对比sklearn官方demo） - sciengieer的文章 - 知乎 https://zhuanlan.zhihu.com/p/390002941

李宏毅课程笔记：Quick Introduction of Batch Normalization

本篇是一个很快地介绍,Batch Normalization 这个技术

一、Changing Landscape（不变化的景观）

之前才讲过说,我们能不能够直接改error surface 的 landscape,我们觉得说 error surface 如果很崎嶇的时候,它比较难 train,那我们能不能够直接把山剷平,让它变得比较好 train 呢？

Batch Normalization 就是其中一个,把山剷平的想法。我们一开始就跟大家讲说,不要小看 optimization 这个问题,有时候就算你的 error surface 是 convex的,它就是一个碗的形状,都不见得很好 train。假设你的两个参数啊,它们对 Loss 的斜率差别非常大,在 \(w_1\) 这个方向上面,你的斜率变化很小,在 \(w_2\) 这个方向上面斜率变化很大。

如果是固定的 learning rate,你可能很难得到好的结果,所以我们才说你需要adaptive 的 learning rate、 Adam 等等比较进阶的 optimization 的方法,才能够得到好的结果。

现在我们要从另外一个方向想,直接把难做的 error surface 把它改掉,看能不能够改得好做一点。在做这件事之前,也许我们第一个要问的问题就是,有这一种状况,$w_1 $ 跟 \(w_2\) 它们的斜率差很多的这种状况,到底是从什麼地方来的。

假设我现在有一个非常非常非常简单的 model,它的输入是 \(x_1\) 跟 \(x_2\),它对应的参数就是 $ w_1 $ 跟 \(w_2\),它是一个 linear 的 model,没有 activation function。

$ w_1 $ 乘 \(x_1\),\(w_2\) 乘 \(x_2\) 加上 b 以后就得到 y,然后会计算 y 跟 \(\hat{y}\) 之间的差距当做 e,把所有 training data e 加起来就是你的 Loss，然后去 minimize 你的 Loss，那什麼样的状况我们会產生像上面这样子,比较不好 train 的 error surface 呢？

当我们对 $ w_1 $ 有一个小小的改变,比如说加上 delta $ w_1 $ 的时候,那这个 L 也会有一个改变,那这个 $ w_1 $ 呢,是透过 $ w_1 $ 改变的时候,你就改变了 y,y 改变的时候你就改变了 e,然后接下来就改变了 L。

那什麼时候 $ w_1 $ 的改变会对 L 的影响很小呢,也就是它在 error surface 上的斜率会很小呢？一个可能性是当你的 input 很小的时候,假设 \(x_1\) 的值在不同的 training example 裡面,它的值都很小,那因為 \(x_1\) 是直接乘上 $ w_1 $，如果 \(x_1\) 的值都很小,$ w_1 $ 有一个变化的时候,它得到的,它对 y 的影响也是小的,对 e 的影响也是小的,它对 L 的影响就会是小的。反之呢,如果今天是 \(x_2\) 的话。

那假设 \(x_2\) 的值都很大,当你的 \(w_2\) 有一个小小的变化的时候,虽然 \(w_2\) 这个变化可能很小,但是因為它乘上了 \(x_2\),\(x_2\) 的值很大,那 y 的变化就很大,那 e 的变化就很大,那 L 的变化就会很大,就会导致我们在 w 这个方向上,做变化的时候,我们把 w 改变一点点,那我们的 error surface 就会有很大的变化。

所以你发现说,既然在这个 linear 的 model 裡面,当我们 input 的 feature,每一个 dimension 的值,它的 scale 差距很大的时候,我们就可能產生像这样子的 error surface,就可能產生不同方向,斜率非常不同,坡度非常不同的 error surface。

所以怎麼办呢,我们有没有可能给feature 裡面不同的 dimension,让它有同样的数值的范围。

如果我们可以给不同的 dimension,同样的数值范围的话,那我们可能就可以製造比较好的 error surface,让 training 变得比较容易一点

其实有很多不同的方法,这些不同的方法,往往就合起来统称為Feature Normalization

二、Feature Normalization

以下所讲的方法只是Feature Normalization 的一种可能性,它并不是 Feature Normalization 的全部,假设 \(x^1\) 到 \(x^R\),是我们所有的训练资料的 feature vector

我们把所有训练资料的 feature vector ,统统都集合起来,那每一个 vector ,\(x_1\) 裡面就 $x^1_1 $代表 \(x_1\) 的第一个 element,$x^2_1 $,就代表 \(x_2\) 的第一个 element,以此类推

那我们把不同笔资料即不同 feature vector,同一个 dimension 裡面的数值,把它取出来,然后去计算某一个 dimension 的 mean，它的 mean 呢 就是\(m_i\)，我们计算第 i 个 dimension 的,standard deviation,我们用\(\sigma_i\)来表示它

那接下来我们就可以做一种 normalization,那这种 normalization 其实叫做标準化,其实叫 standardization,不过我们这边呢,就等一下都统称 normalization 就好了 \[ \tilde{x}^r_i ← \frac{x^r_i-m_i}{\sigma_i} \] 我们就是把这边的某一个数值x,减掉这一个 dimension 算出来的 mean,再除掉这个 dimension,算出来的 standard deviation,得到新的数值叫做 \(\tilde{x}\)

然后得到新的数值以后,再把新的数值把它塞回去,以下都用这个 tilde来代表有被 normalize 后的数值

那做完 normalize 以后有什麼好处呢？

• 做完 normalize 以后啊,这个 dimension 上面的数值就会平均是 0,然后它的 variance就会是 1,所以这一排数值的分布就都会在 0 上下

• 对每一个 dimension都做一样的 normalization,就会发现所有 feature 不同 dimension 的数值都在 0 上下,那你可能就可以製造一个,比较好的 error surface

所以像这样子 Feature Normalization 的方式,往往对你的 training 有帮助,它可以让你在做 gradient descent 的时候,这个 gradient descent,它的 Loss 收敛更快一点,可以让你的 gradient descent,它的训练更顺利一点,这个是 Feature Normalization

三、Considering Deep Learning

\(\tilde{x}\) 代表 normalize 的 feature,把它丢到 deep network 裡面,去做接下来的计算和训练,所以把 \(x_1\) tilde 通过第一个 layer 得到 \(z^1\),那你有可能通过 activation function,不管是选 Sigmoid 或者 ReLU 都可以,然后再得到 \(a^1\),然后再通过下一层等等,那就看你有几层 network 你就做多少的运算

所以每一个 x 都做类似的事情,但是如果我们进一步来想的话,对 \(w_2\) 来说

这边的 \(a^1\) \(a^3\) 这边的 \(z^1\) \(z^3\),其实也是另外一种 input,如果这边 \(\tilde{x}\),虽然它已经做 normalize 了,但是通过 $ w_1 $ 以后它就没有做 normalize,如果 \(\tilde{x}\) 通过 $ w_1 $ 得到是 \(z^1\),而 \(z^1\) 不同的 dimension 间,它的数值的分布仍然有很大的差异的话,那我们要 train \(w_2\) 第二层的参数,会不会也有困难呢

对 \(w_2\) 来说,这边的 a 或这边的 z 其实也是一种 feature,我们应该要对这些 feature 也做 normalization

那如果你选择的是 Sigmoid,那可能比较推荐对 z 做 Feature Normalization,因為Sigmoid 是一个 s 的形状,那它在 0 附近斜率比较大,所以如果你对 z 做 Feature Normalization,把所有的值都挪到 0 附近,那你到时候算 gradient 的时候,算出来的值会比较大

那不过因為你不见得是用 sigmoid ,所以你也不一定要把 Feature Normalization放在 z 这个地方,如果是选别的,也许你选a也会有好的结果,也说不定，Ingeneral 而言,这个 normalization,要放在 activation function 之前,或之后都是可以的,在实作上,可能没有太大的差别,好 那我们这边呢,就是对 z 呢,做一下 Feature Normalization，

那怎麼对 z 做 Feature Normalization 呢

那你就把 z,想成是另外一种 feature ,我们这边有 \(z^1\) \(z^2\) \(z^3\),我们就把 \(z^1\) \(z^2\) \(z^3\) 拿出来

• 算一下它的 mean，这边的 \(μ\) 是一个 vector,我们就把 \(z^1\) \(z^2\) \(z^3\),这三个 vector 呢,把它平均起来,得到 \(μ\) 这个 vector
• 算一个 standard deviation,这个 standard deviation 呢,这边这个成 \(\sigma\),它也代表了一个 vector,那这个 vector 怎麼算出来呢,你就把 \(z^i\)减掉 \(μ\),然后取平方,这边的平方,这个 notation 有点 abuse 啊,这边的平方就是指,对每一个 element 都去做平方,然后再开根号,这边开根号指的是对每一个 element,向量裡面的每一个 element,都去做开根号,得到 \(\sigma\),反正你知道我的意思就好

把这三个 vector,裡面的每一个 dimension,都去把它的 \(μ\) 算出来,把它的 \(\sigma\) 算出来,好 我这边呢,就不把那些箭头呢 画出来了,从 \(z^1\) \(z^2\) \(z^3\),算出 \(μ\),算出 \(\sigma\)。

接下来就把这边的每一个 z ,都去减掉 \(μ\) 除以 \(\sigma\),你把 \(z^i\)减掉 \(μ\),除以 \(\sigma\),就得到 \(z^i\)的 tilde。

那这边的 \(μ\) 跟 \(\sigma\),它都是向量,所以这边这个除的意思是element wise 的相除,就是 \(z^i\)减 \(μ\),它是一个向量,所以分子的地方是一个向量,分母的地方也是一个向量,把这个两个向量,它们对应的 element 的值相除,是我这边这个除号的意思,这边得到 Z 的 tilde。

所以我们就是把 \(z^1\) 减 \(μ\) 除以 \(\sigma\),得到 \(z^1\) tilde,同理 \(z^2\) 减 \(μ\) 除以 \(\sigma\),得到 \(z^2\) tilde,\(z^3\) 减 \(μ\) 除以 \(\sigma\),得到 \(z^3\) tilde,那就把这个 \(z^1\) \(z^2\) \(z^3\),做 Feature Normalization,变成 \(z^1\) tilde,\(z^2\) tilde 跟 \(z^3\) 的 tilde。

接下来就看你爱做什麼 就做什麼啦,通过 activation function,得到其他 vector,然后再通过,再去通过其他 layer 等等,这样就可以了,这样你就等於对 \(z^1\) \(z^2\) \(z^3\),做了 Feature Normalization,变成 \(\tilde{z}^1\) \(\tilde{z}^2\) \(\tilde{z}^3\) 。

在这边有一件有趣的事情,这边的 \(μ\) 跟 \(\sigma\),它们其实都是根据 \(z^1\) \(z^2\) \(z^3\) 算出来的。

所以这边 \(z^1\) 啊,它本来,如果我们没有做 Feature Normalization 的时候,你改变了 \(z^1\) 的值,你会改变这边 a 的值,但是现在啊,当你改变 \(z^1\) 的值的时候,\(μ\) 跟 \(\sigma\) 也会跟著改变,\(μ\) 跟 \(\sigma\) 改变以后,\(z^2\) 的值 \(a^2\) 的值,\(z^3\) 的值 \(a^3\) 的值,也会跟著改变。

所以之前,我们每一个 \(\tilde{x}_1\) \(\tilde{x}_2\) \(\tilde{x}_3\),它是独立分开处理的,但是我们在做 Feature Normalization 以后,这三个 example,它们变得彼此关联了。

我们这边 \(z^1\) 只要有改变,接下来 \(z^2\) \(a^2\) \(z^3\) \(a^3\),也都会跟著改变,所以这边啊,其实你要把,当你有做 Feature Normalization 的时候,你要把这一整个 process,就是有收集一堆 feature,把这堆 feature 算出 \(μ\) 跟 \(\sigma\) 这件事情,当做是 network 的一部分。

也就是说,你现在有一个比较大的 network

• 你之前的 network,都只吃一个 input,得到一个 output
• 现在你有一个比较大的 network,这个大的 network,它是吃一堆 input,用这堆 input 在这个 network 裡面,要算出 \(μ\) 跟 \(\sigma\),然后接下来產生一堆 output

那这个地方比较抽象,只可会意 不可言传这样子

那这边就会有一个问题了,因為你的训练资料裡面的 data 非常多,现在一个 data set,benchmark corpus 都上百万笔资料， GPU 的 memory,根本没有办法,把它整个 data set 的 data 都 load 进去。

在实作的时候,你不会让这一个 network 考虑整个 training data 裡面的所有 example,你只会考虑一个 batch 裡面的 example,举例来说,你 batch 设 64,那你这个巨大的 network,就是把 64 笔 data 读进去,算这 64 笔 data 的 \(μ\),算这 64 笔 data 的 \(\sigma\),对这 64 笔 data 都去做 normalization

因為我们在实作的时候,我们只对一个 batch 裡面的 data,做 normalization,所以这招叫做 Batch Normalization

那这个 Batch Normalization,显然有一个问题 就是,你一定要有一个够大的 batch,你才算得出 \(μ\) 跟 \(\sigma\),假设你今天,你 batch size 设 1,那你就没有什麼 \(μ\) 或 \(\sigma\) 可以算

所以这个 Batch Normalization,是适用於 batch size 比较大的时候,因為 batch size 如果比较大,也许这个 batch size 裡面的 data,就足以表示,整个 corpus 的分布,那这个时候你就可以,把这个本来要对整个 corpus,做 Feature Normalization 这件事情,改成只在一个 batch,做 Feature Normalization,作為 approximation。

在做 Batch Normalization 的时候,往往还会有这样的设计你算出这个 \(\tilde{z}\) 以后

• 接下来你会把这个 \(\tilde{z}\),再乘上另外一个向量叫做 \(γ\),这个 \(γ\) 也是一个向量,所以你就是把 \(\tilde{z}\) 跟 \(γ\) 做 element wise 的相乘,把 z 这个向量裡面的 element,跟 \(γ\) 这个向量裡面的 element,两两做相乘。
• 再加上 \(β\) 这个向量,得到 \(\hat{z}\)。

而 \(β\) 跟 \(γ\),你要把它想成是 network 的参数,它是另外再被learn出来的,

那為什麼要加上 \(β\) 跟 \(γ\) 呢？

有人可能会觉得说,如果我们做 normalization 以后,那这边的 \(\tilde{z}\),它的平均就一定是 0,那也许,今天如果平均是 0 的话,就是给那 network 一些限制,那也许这个限制会带来什麼负面的影响,所以我们把 \(β\) 跟 \(γ\) 加回去。

然后让 network 呢,现在它的 hidden layer 的 output平均不是 0 的话,他就自己去learn这个 \(β\) 跟 \(γ\),来调整一下输出的分布,来调整这个 \(\hat{z}\) 的分布

但讲到这边又会有人问说,刚才不是说做 Batch Normalization 就是,為了要让每一个不同的 dimension,它的 range 都是一样吗,现在如果加去乘上 \(γ\),再加上 \(β\),把 \(γ\) 跟 \(β\) 加进去,

这样不会不同 dimension 的分布,它的 range 又都不一样了吗？

有可能,但是你实际上在训练的时候,这个 \(γ\) 跟 \(β\) 的初始值啊

• 你会把这个 \(γ\) 的初始值 就都设為 1,所以 \(γ\) 是一个裡面的值,一开始其实是一个裡面的值,全部都是 1 的向量
• 那 \(β\) 是一个裡面的值,全部都是 0 的向量,所以 \(γ\) 是一个 one vector,都是 1 的向量,\(β\) 是一个 zero vector,裡面的值都是 0 的向量

所以让你的 network 在一开始训练的时候,每一个 dimension 的分布,是比较接近的,也许训练到后来,你已经训练够长的一段时间,已经找到一个比较好的 error surface,走到一个比较好的地方以后,那再把 \(γ\) 跟 \(β\) 慢慢地加进去,好所以加 Batch Normalization,往往对你的训练是有帮助的。

四、Testing

这个 Batch Normalization 在 inference,或是 testing 的时候,会有什麼样的问题呢？

在 testing 的时候,如果 当然如果今天你是在做作业,我们一次会把所有的 testing 的资料给你,所以你确实也可以在 testing 的资料上面,製造一个一个 batch。

但是假设你真的有系统上线,你是一个真正的线上的 application,你可以说,我今天一定要等 30,比如说你的 batch size 设 64,我一定要等 64 笔资料都进来,我才一次做运算吗,这显然是不行的。

但是在做 Batch Normalization 的时候,一个 \(\tilde{x}\),一个 normalization 过的 feature 进来,然后你有一个 z,你的 z 呢,要减掉 \(μ\) 跟除 \(\sigma\),那这个 \(μ\) 跟 \(\sigma\),是用一个 batch 的资料算出来的

但如果今天在 testing 的时候,根本就没有 batch,那我们要怎麼算这个 \(μ\),跟怎麼算这个 \(\sigma\) 呢？

所以真正的,这个实作上的解法是这个样子的,如果你看那个 PyTorch 的话呢,Batch Normalization 在 testing 的时候,你并不需要做什麼特别的处理,PyTorch 帮你处理好了

在 training 的时候,如果你有在做 Batch Normalization 的话,在 training 的时候,你每一个 batch 计算出来的 \(μ\) 跟 \(\sigma\),他都会拿出来算 moving average

你每一次取一个 batch 出来的时候,你就会算一个 \(μ^1\),取第二个 batch 出来的时候,你就算个 \(μ^2\),一直到取第 t 个 batch 出来的时候,你就算一个 \(μ^t\) 。接下来你会算一个 moving average,你会把你现在算出来的 \(μ\) 的一个平均值,叫做 \(μ\) bar,乘上某一个 factor,那这也是一个常数,这个这也是一个 constant,这也是一个那个 hyper parameter,也是需要调的。

在 PyTorch 裡面,我没记错 他就设 0.1,我记得他 P 就设 0.1,好,然后加上 1 减 P,乘上 \(μ^t\) ,然后来更新你的 \(μ\) 的平均值,然后最后在 testing 的时候,你就不用算 batch 裡面的 \(μ\) 跟 \(\sigma\) 了。

因為 testing 的时候,在真正 application 上,也没有 batch 这个东西,你就直接拿 \(\barμ\) 跟 \(\bar\sigma\) ,也就是 \(μ\) 跟 \(\sigma\) 在训练的时候,得到的 moving average,\(\barμ\) 跟 \(\bar\sigma\) ,来取代这边的 \(μ\) 跟 \(\sigma\),这个就是 Batch Normalization,在 testing 的时候的运作方式。

五、Comparison

好 那这个是从 Batch Normalization,原始的文件上面截出来的一个实验结果,那在原始的文件上还讲了很多其他的东西,举例来说,我们今天还没有讲的是,Batch Normalization 用在 CNN 上,要怎麼用呢,那你自己去读一下原始的文献,裡面会告诉你说,Batch Normalization 如果用在 CNN 上,应该要长什麼样子。

卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。

卷积神经网络经过卷积后得到的是一系列的特征图，如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,f,p,q)，m为min-batch sizes，f为特征图个数，p、q分别为特征图的宽高。

在cnn中我们可以把每个特征图看成是一个特征处理（一个神经元），因此在使用Batch Normalization，mini-batch size 的大小就是：m * p * q，于是对于每个特征图都只有一对可学习参数：γ、β。

相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。

• nb在每一个特征图上的所有点沿着一个batch的样本数据的方向对数据进行求和，求平均等处理，不考虑不同特征图的数据间的运算。
• lrb在每一个特征图上沿着不同特征图的方向对数据进行求和，求平均等处理，不考虑不同输入样本数据间的运算。

这个是原始文献上面截出来的一个数据

• 横轴呢,代表的是训练的过程，纵轴代表的是 validation set 上面的 accuracy
• 那这个黑色的虚线是没有做 Batch Normalization 的结果,它用的是 inception 的 network,就是某一种 network 架构啦,也是以 CNN 為基础的 network 架构
• 然后如果有做 Batch Normalization,你会得到红色的这一条虚线,那你会发现说,红色这一条虚线,它训练的速度,显然比黑色的虚线还要快很多,虽然最后收敛的结果啊,就你只要给它足够的训练的时间,可能都跑到差不多的 accuracy,但是红色这一条虚线,可以在比较短的时间内,就跑到一样的 accuracy,那这边这个蓝色的菱形,代表说这几个点的那个 accuracy 是一样的
• 粉红色的线是 sigmoid function,就 sigmoid function 一般的认知,我们虽然还没有讨论这件事啦,但一般都会选择 ReLu,而不是用 sigmoid function,因為 sigmoid function,它的 training 是比较困难的,但是这边想要强调的点是说,就算是 sigmoid 比较难搞的,加 Batch Normalization,还是 train 的起来,那这边没有 sigmoid,没有做 Batch Normalization 的结果,因為在这个实验上,作者有说,sigmoid 不加 Batch Normalization,根本连 train 都 train 不起来
• 蓝色的实线跟这个蓝色的虚线呢,是把 learning rate 设比较大一点,乘 5,就是 learning rate 变原来的 5 倍,然后乘 30,就是 learning rate 变原来的 30 倍,那因為如果你做 Batch Normalization 的话,那你的 error surface 呢,会比较平滑 比较容易训练,所以你可以把你的比较不崎嶇,所以你就可以把你的 learning rate 呢,设大一点

六、Internal Covariate Shift?

好接下来的问题就是,Batch Normalization,它為什麼会有帮助呢,在原始的 Batch Normalization,那篇 paper 裡面,他提出来一个概念,叫做internal covariate shift,covariate shift(训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象) 这个词汇是原来就有的,internal covariate shift,我认為是,Batch Normalization 的作者自己发明的。他认為说今天在 train network 的时候,会有以下这个问题,这个问题是这样。

network 有很多层

• x 通过第一层以后 得到 a

• a 通过第二层以后 得到 b

• 计算出 gradient 以后,把 A update 成 A′,把 B 这一层的参数 update 成 B′

但是作者认為说,我们在计算 B,update 到 B′ 的 gradient 的时候,这个时候前一层的参数是 A 啊,或者是前一层的 output 是小 a 啊

那当前一层从 A 变成 A′ 的时候,它的 output 就从小 a 变成小 a′ 啊

但是我们计算这个 gradient 的时候,我们是根据这个 a 算出来的啊,所以这个 update 的方向,也许它适合用在 a 上,但不适合用在 a′ 上面

那如果说 Batch Normalization 的话,我们会让,因為我们每次都有做 normalization,我们就会让 a 跟 a′ 呢,它的分布比较接近,也许这样就会对训练呢,有帮助。

但是有一篇 paper 叫做,How Does Batch Normalization,Help Optimization,然后他就打脸了internal covariate shift 的这一个观点。

在这篇 paper 裡面,他从各式各样的面向来告诉你说,internal covariate shift,首先它不一定是 training network 的时候的一个问题,然后 Batch Normalization,它会比较好,可能不见得是因為,它解决了 internal covariate shift。

那在这篇 paper 裡面呢,他做了很多很多的实验,比如说他比较了训练的时候,这个 a 的分布的变化 发现,不管有没有做 Batch Normalization,它的变化都不大。

然后他又说,就算是变化很大,对 training 也没有太大的伤害,然后他又说,不管你是根据 a 算出来的 gradient,还是根据 a′ 算出来的 gradient,方向居然都差不多。

所以他告诉你说,internal covariate shift,可能不是 training network 的时候,最主要的问题,它可能也不是,Batch Normalization 会好的一个的关键,那有关更多的实验,你就自己参见这篇文章。

為什麼 Batch Normalization 会比较好呢？

那在这篇 How Does Batch Normalization,Help Optimization 这篇论文裡面,他从实验上,也从理论上,至少支持了 Batch Normalization,可以改变 error surface,让 error surface 比较不崎嶇这个观点。

所以这个观点是有理论的支持,也有实验的佐证的,那在这篇文章裡面呢,作者还讲了一个非常有趣的话,他说他觉得啊,这个 Batch Normalization 的 positive impact。

因為他说,如果我们要让 network,这个 error surface 变得比较不崎嶇,其实不见得要做 Batch Normalization,感觉有很多其他的方法,都可以让 error surface 变得不崎嶇,那他就试了一些其他的方法,发现说,跟 Batch Normalization performance 也差不多,甚至还稍微好一点,所以他就讲了下面这句感嘆。

他觉得说,这个,positive impact of batchnorm on training,可能是 somewhat,serendipitous,什麼是 serendipitous 呢,这个字眼可能可以翻译成偶然的,但偶然并没有完全表达这个词汇的意思,这个词汇的意思是说,你发现了一个什麼意料之外的东西。

那这篇文章的作者也觉得,Batch Normalization 也像是盘尼西林一样,是一种偶然的发现,但无论如何,它是一个有用的方法。

To learn more ……

那其实 Batch Normalization,不是唯一的 normalization,normalization 的方法有一把啦,那这边就是列了几个比较知名的,

Batch Renormalization https://arxiv.org/abs/1702.03275 Layer Normalization https://arxiv.org/abs/1607.06450 Instance Normalization https://arxiv.org/abs/1607.08022 Group Normalization https://arxiv.org/abs/1803.08494 Weight Normalization https://arxiv.org/abs/1602.07868 Spectrum Normalization https://arxiv.org/abs/1705.10941

李宏毅课程笔记：When gradient is small

一、Critical Point

1.1 Training Fails because

现在我们要讲的是Optimization的部分,所以我们要讲的东西基本上跟Overfitting没有什么太大的关联,我们只讨论Optimization的时候,怎么把gradient descent做得更好,那为什么Optimization会失败呢？

你常常在做Optimization的时候,你会发现,随著你的参数不断的update,你的training的loss不会再下降,但是你对这个loss仍然不满意,就像我刚才说的,你可以把deep的network,跟linear的model,或比较shallow network 比较,发现说它没有做得更好,所以你觉得deepnetwork,没有发挥它完整的力量,所以Optimization显然是有问题的。

但有时候你会甚至发现,一开始你的model就train不起来,一开始你不管怎么update你的参数,你的loss通通都掉不下去,那这个时候到底发生了什么事情呢？

过去常见的一个猜想,是因为我们现在走到了一个地方,这个地方参数对loss的微分为零,当你的参数对loss微分为零的时候,gradient descent就没有办法再update参数了,这个时候training就停下来了,loss当然就不会再下降了。

讲到gradient为零的时候,大家通常脑海中最先浮现的,可能就是local minima,所以常有人说做deep learning,用gradient descent会卡在local minima,然后所以gradient descent不work,所以deep learning不work。

但是如果有一天你要写,跟deep learning相关paper的时候,你千万不要讲卡在local minima这种事情,别人会觉得你非常没有水准,为什么？

因为不是只有local minima的gradient是零,还有其他可能会让gradient是零,比如说 saddle point,所谓的saddle point,其实就是gradient是零,但是不是local minima,也不是local maxima的地方,像在右边这个例子里面 红色的这个点,它在左右这个方向是比较高的,前后这个方向是比较低的,它就像是一个马鞍的形状,所以叫做saddle point,那中文就翻成鞍点。

像saddle point这种地方,它也是gradient为零,但它不是local minima,那像这种gradient为零的点,统称为critical point,所以你可以说你的loss,没有办法再下降,也许是因为卡在了critical point,但你不能说是卡在local minima,因为saddle point也是微分为零的点

但是今天如果你发现你的gradient,真的很靠近零,卡在了某个critical point,我们有没有办法知道,到底是local minima,还是saddle point？其实是有办法的

为什么我们想要知道到底是卡在local minima,还是卡在saddle point呢

• 因为如果是卡在local minima,那可能就没有路可以走了,因为四周都比较高,你现在所在的位置已经是最低的点,loss最低的点了,往四周走 loss都会比较高,你会不知道怎么走到其他的地方去
• 但saddle point就比较没有这个问题,如果你今天是卡在saddle point的话,saddle point旁边还是有路可以走的,还是有路可以让你的loss更低的,你只要逃离saddle point,你就有可能让你的loss更低

所以鉴别今天我们走到,critical point的时候,到底是local minima,还是saddle point,是一个值得去探讨的问题,那怎么知道今天一个critical point,到底是属于local minima,还是saddle point呢？

1.2 Warning of Math

这边需要用到一点数学,以下这段其实没有很难的数学,就只是微积分跟线性代数,但如果你没有听懂的话,以下这段skip掉是没有关系的，那怎么知道说一个点,到底是local minima,还是saddle point呢？

你要知道我们loss function的形状,可是我们怎么知道,loss function的形状呢,network本身很复杂,用复杂network算出来的loss function,显然也很复杂,我们怎么知道loss function,长什么样子,虽然我们没有办法完整知道,整个loss function的样子

Tayler Series Approximation

但是如果给定某一组参数,比如说蓝色的这个\(θ'\),在\(θ'\)附近的loss function,是有办法被写出来的,它写出来就像是这个样子：

所以这个\(L(θ)\)完整的样子写不出来,但是它在\(θ'\)附近,你可以用这个式子来表示它,这个式子是,Tayler Series Appoximation泰勒级数展开,这个假设你在微积分的时候,已经学过了,所以我就不会细讲这一串是怎么来的,但我们就只讲一下它的概念,这一串里面包含什么东西呢?

• 第一项是\(L(θ')\),就告诉我们说,当\(θ\)跟\(θ'\)很近的时候,\(L(θ)\)应该跟\(L(θ')\)还蛮靠近的

• 第二项是\((θ-θ')^Tg\)

  

  \(g\)是一个向量,这个g就是我们的gradient,我们用绿色的这个g来代表gradient,这个gradient会来弥补,\(θ'\)跟\(θ\)之间的差距,我们虽然刚才说\(θ'\)跟\(θ\),它们应该很接近,但是中间还是有一些差距的,那这个差距,第一项我们用这个gradient,来表示他们之间的差距,有时候gradient会写成\(∇L(θ')\),这个地方的\(g\)是一个向量,它的第i个component,就是θ的第i个component对L的微分,光是看g还是没有办法,完整的描述L(θ),你还要看第三项

• 第三项跟Hessian有关,这边有一个$H $

  

  这个\(H\)叫做Hessian,它是一个矩阵,这个第三项是,再\((θ-θ')^TH(θ-θ')\),所以第三项会再补足,再加上gradient以后,与真正的L(θ)之间的差距.H里面放的是L的二次微分,它第i个row,第j个column的值,就是把θ的第i个component,对L作微分,再把θ的第j个component,对L作微分,再把θ的第i个component,对L作微分,做两次微分以后的结果 就是这个\(H_i{_j}\)

如果这边你觉得有点听不太懂的话,也没有关系,反正你就记得这个\(L(θ)\),这个loss function,这个error surface在\(θ'\)附近,可以写成这个样子,这个式子跟两个东西有关系,跟gradient有关系,跟hessian有关系,gradient就是一次微分,hessian就是里面有二次微分的项目

Hession

那如果我们今天走到了一个critical point,意味著gradient为零,也就是绿色的这一项完全都不见了

\(g\)是一个zero vector,绿色的这一项完全都不见了,只剩下红色的这一项,所以当在critical point的时候,这个loss function,它可以被近似为\(L(θ')\),加上红色的这一项。我们可以根据红色的这一项来判断,在\(θ'\)附近的error surface,到底长什么样子。知道error surface长什么样子,我就可以判断。

判断 \(θ'\)它是一个local minima,还是一个saddle point。

我们可以靠这一项来了解,这个error surface的地貌,大概长什么样子,知道它地貌长什么样子,我们就可以知道说,现在是在什么样的状态,这个是Hessian。

那我们就来看一下怎么根据Hessian,怎么根据红色的这一项,来判断θ'附近的地貌。

我们现在为了等一下符号方便起见,我们把\((θ-θ')\)用\(v\)这个向量来表示

• 如果今天对任何可能的\(v\),\(v^THv\)都大于零,也就是说 现在θ不管代任何值,v可以是任何的v,也就是θ可以是任何值,不管θ代任何值,红色框框里面通通都大于零,那意味著说 \(L(θ)>L(θ')\)。\(L(θ)\)不管代多少 只要在\(θ'\)附近,\(L(θ)\)都大于\(L(θ')\),代表\(L(θ')\)是附近的一个最低点,所以它是local minima
• 如果今天反过来说,对所有的\(v\)而言,\(v^THv\)都小于零,也就是红色框框里面永远都小于零,也就是说\(θ\)不管代什么值,红色框框里面都小于零,意味著说\(L(θ)<L(θ')\),代表\(L(θ')\)是附近最高的一个点,所以它是local maxima
• 第三个可能是假设,\(v^THv\),有时候大于零 有时候小于零,你代不同的v进去 代不同的θ进去,红色这个框框里面有时候大于零,有时候小于零,意味著说在θ'附近,有时候L(θ)>L(θ') 有时候L(θ)<L(θ'),在L(θ')附近,有些地方高 有些地方低,这意味著什么,这意味著这是一个saddle point

但是你这边是说我们要代所有的\(v\),去看\(v^THv\)是大于零,还是小于零.我们怎么有可能把所有的v,都拿来试试看呢,所以有一个更简便的方法,去确认说这一个条件或这一个条件,会不会发生.

这个就直接告诉你结论,线性代数理论上是有教过这件事情的,如果今天对所有的v而言,\(v^THv\)都大于零,那这种矩阵叫做positive definite 正定矩阵,positive definite的矩阵,它所有的eigen value特征值都是正的

所以如果你今天算出一个hessian,你不需要把它跟所有的v都乘看看,你只要去直接看这个H的eigen value,如果你发现：

• 所有eigen value都是正的,那就代表说这个条件成立,就\(v^THv\),会大于零,也就代表说是一个local minima。所以你从hessian metric可以看出,它是不是local minima,你只要算出hessian metric算完以后,看它的eigen value发现都是正的,它就是local minima。
• 那反过来说也是一样,如果今天在这个状况,对所有的v而言,\(v^THv\)小于零,那H是negative definite,那就代表所有eigen value都是负的,就保证他是local maxima
• 那如果eigen value有正有负,那就代表是saddle point,

那假设在这里你没有听得很懂的话,你就可以记得结论,你只要算出一个东西,这个东西的名字叫做hessian,它是一个矩阵,这个矩阵如果它所有的eigen value,都是正的,那就代表我们现在在local minima,如果它有正有负,就代表在saddle point。

那如果刚才讲的,你觉得你没有听得很懂的话,我们这边举一个例子：

我们现在有一个史上最废的network,输入一个x,它只有一个neuron，乘上\(w₁\),而且这个neuron,还没有activation function,所以x乘上\(w₁\)以后 之后就输出,然后再乘上\(w₂\) 然后就再输出,就得到最终的数据就是y.总之这个function非常的简单 \[ y= w₁×w₂×x \] 我们有一个史上最废的training set,这个data set说,我们只有一笔data,这笔data是x,是1的时候,它的level是1 所以输入1进去,你希望最终的输出跟1越接近越好

而这个史上最废的training,它的error surface,也是有办法直接画出来的,因为反正只有两个参数 w₁ w₂,连bias都没有,假设没有bias,只有w₁跟w₂两个参数,这个network只有两个参数 w₁跟w₂,那我们可以穷举所有w₁跟w₂的数值,算出所有w₁ w₂数值所代来的loss,然后就画出error surface 长这个样

四个角落loss是高的,好 那这个图上你可以看出来说,有一些critical point,这个黑点点的地方(0,0),原点的地方是critical point,然后事实上,右上三个黑点也是一排critical point,左下三个点也是一排critical point。如果你更进一步要分析,他们是saddle point,还是local minima的话,那圆心这个地方,原点这个地方 它是saddle point,为什么它是saddle point呢？你往左上这个方向走 loss会变大,往右下这个方向走 loss会变大,往左下这个方向走 loss会变小,往右下这个方向走 loss会变小,它是一个saddle point。

而这两群critical point,它们都是local minima,所以这个山沟里面,有一排local minima,这一排山沟里面有一排local minima,然后在原点的地方,有一个saddle point,这个是我们把error surface,暴力所有的参数,得到的loss function以后,得到的loss的值以后,画出error surface,可以得到这样的结论。

现在假设如果不暴力所有可能的loss,如果要直接算说一个点,是local minima,还是saddle point的话 怎么算呢

我们可以把loss的function写出来,这个loss的function 这个L是 \[ L=(\hat{y}-w_1 w_2 x)^2 \] 正确答案 ŷ减掉model的输出,也就是w₁ w₂x,这边取square error,这边只有一笔data,所以就不会summation over所有的training data,因为反正只有一笔data,x代1 ŷ代1,我刚才说过只有一笔训练资料最废的,所以只有一笔训练资料,所以loss function就是\(L=(\hat{y}-w_1 w_2 x)^2\),那你可以把这一个loss function,它的gradient求出来,w₁对L的微分,w₂对L的微分写出来是这个样子 \[ \frac{∂L}{∂w_1 }=2(1-w_1 w_2 )(-w_2 ) \]

\[ \frac{∂L}{∂w_2 }=2(1-w_1 w_2 )(-w_1 ) \]

​ 这个东西 \[ \begin{bmatrix} \frac{∂L}{∂w_1 }\\\ \frac{∂L}{∂w_2 } \end{bmatrix} \] 就是所谓的g,所谓的gradient,什么时候gradient会零呢,什么时候会到一个critical point呢?

举例来说 如果w₁=0 w₂=0,就在圆心这个地方,如果w₁代0 w₂代0,w₁对L的微分 w₂对L的微分,算出来就都是零 就都是零,这个时候我们就知道说,原点就是一个critical point,但它是local maxima,它是local maxima,local minima,还是saddle point呢,那你就要看hessian才能够知道了

当然 我们刚才已经暴力所有可能的w₁ w₂了,所以你已经知道说,它显然是一个saddle point,但是现在假设还没有暴力所有可能的loss,所以我们要看看能不能够用H,用Hessian看出它是什么样的critical point,那怎么算出这个H呢？

H它是一个矩阵,这个矩阵里面元素就是L的二次微分,所以这个矩阵里面第一个row,第一个coloumn的位置,就是w₁对L微分两次,第一个row 第二个coloumn的位置,就是先用w₂对L作微分,再用w₁对L作微分,然后这边就是w₁对L作微分,w₂对L作微分,然后w₂对L微分两次,这四个值组合起来,就是我们的hessian,那这个hessian的值是多少呢

这个hessian的式子,我都已经把它写出来了,你只要把w₁=0 w₂=0代进去,代进去 你就得到在原点的地方,hessian是这样的一个矩阵 \[ \begin{bmatrix} {0}&-2\\\ {-2}&0 \end{bmatrix} \] 这个hessian告诉我们,它是local minima,还是saddle point呢,那你就要看这个矩阵的eigen value,算一下发现,这个矩阵有两个eigen value,2跟-2 eigen value有正有负,代表saddle point

所以我们现在就是用一个例子,跟你操作一下 告诉你说,你怎么从hessian看出一个点,它一个critical point 它是saddle point,还是local minima

1.3 Don't afraid of saddle point

如果今天你卡的地方是saddle point,也许你就不用那么害怕了,因为如果你今天你发现,你停下来的时候,是因为saddle point 停下来了,那其实就有机会可以放心了。

因为H它不只可以帮助我们判断,现在是不是在一个saddle point,它还指出了我们参数,可以update的方向,就之前我们参数update的时候,都是看gradient 看g,但是我们走到某个地方以后,发现g变成0了 不能再看g了,g不见了 gradient没有了,但如果是一个saddle point的话,还可以再看H,怎么再看H呢,H怎么告诉我们,怎么update参数呢

我们这边假设\(\mu\)是H的eigenvector特征向量,然后\(λ\)是u的eigen value特征值。如果我们把这边的\(v\)换成\(\mu\)的话,我们把\(\mu\)乘在H的左边,跟H的右边,也就是\(\mu^TH\mu\), \(H\mu\)会得到\(λ\mu\)，因为\(\mu\)是一个eigen vector。H乘上eigen vector特征向量会得到特征向量λ eigen value乘上eigen vector即\(λ\mu\)

所以我们在这边得到uᵀ乘上λu,然后再整理一下,把uᵀ跟u乘起来,得到‖u‖²,所以得到λ‖u‖²

假设我们这边v,代的是一个eigen vector,我们这边θ减θ',放的是一个eigen vector的话,会发现说我们这个红色的项里面,其实就是λ‖u‖²

那今天如果λ小于零,eigen value小于零的话,那λ‖u‖²就会小于零,因为‖u‖²一定是正的,所以eigen value是负的,那这一整项就会是负的,也就是u的transpose乘上H乘上u,它是负的,也就是红色这个框里是负的。所以这意思是说假设\(θ-θ'=\mu\),那这一项\((θ-θ')^TH(θ-θ')\)就是负的,也就是\(L(θ)<L(θ')\)。也就是说假设\(θ-θ'=\mu\),也就是,你在θ'的位置加上u,沿著u的方向做update得到θ,你就可以让loss变小。

因为根据这个式子,你只要θ减θ'等于u,loss就会变小,所以你今天只要让θ等于θ'加u,你就可以让loss变小,你只要沿著u,也就是eigen vector的方向,去更新你的参数 去改变你的参数,你就可以让loss变小了

所以虽然在critical point没有gradient,如果我们今天是在一个saddle point,你也不一定要惊慌,你只要找出负的eigen value,再找出它对应的eigen vector,用这个eigen vector去加θ',就可以找到一个新的点,这个点的loss比原来还要低。

举具体的例子：

刚才我们已经发现,原点是一个critical point,它的Hessian长这个样,那我现在发现说,这个Hessian有一个负的eigen value,这个eigen value等于-2,那它对应的eigen vector,它有很多个,其实是无穷多个对应的eigen vector,我们就取一个出来,我们取\(\begin{bmatrix}{1} \\\ {1}\end{bmatrix}\)是它对应的一个eigen vector,那我们其实只要顺著这个u的方向,顺著\(\begin{bmatrix}{1} \\\ {1}\end{bmatrix}\)这个vector的方向,去更新我们的参数,就可以找到一个,比saddle point的loss还要更低的点。

如果以今天这个例子来看的话,你的saddle point在(0,0)这个地方,你在这个地方会没有gradient,Hessian的eigen vector告诉我们,只要往\(\begin{bmatrix}{1} \\\ {1}\end{bmatrix}\)的方向更新,你就可以让loss变得更小,也就是说你可以逃离你的saddle point,然后让你的loss变小,所以从这个角度来看,似乎saddle point并没有那么可怕。如果你今天在training的时候,你的gradient你的训练停下来,你的gradient变成零,你的训练停下来,是因为saddle point的话,那似乎还有解。

但是当然实际上,在实际的implementation里面,你几乎不会真的把Hessian算出来,这个要是二次微分,要计算这个矩阵的computation,需要的运算量非常非常的大,更遑论你还要把它的eigen value,跟 eigen vector找出来,所以在实作上,你几乎没有看到,有人用这一个方法来逃离saddle point。

等一下我们会讲其他,也有机会逃离saddle point的方法,他们的运算量都比要算这个H,还要小很多,那今天之所以我们把,这个saddle point跟 eigen vector,跟Hessian的eigen vector拿出来讲,是想要告诉你说,如果是卡在saddle point,也许没有那么可怕,最糟的状况下你还有这一招,可以告诉你要往哪一个方向走.

1.4 Saddle Point v.s. Local Minima

讲到这边你就会有一个问题了,这个问题是,那到底saddle point跟local minima,谁比较常见呢,我们说,saddle point其实并没有很可怕,那如果我们今天,常遇到的是saddle point,比较少遇到local minima,那就太好了,那到底saddle point跟local minima,哪一个比较常见呢?

总之这个从三维的空间来看,是没有路可以走的东西,在高维的空间中是有路可以走的,error surface会不会也一样呢？

而经验上,如果你自己做一些实验的话,也支持这个假说

这边是训练某一个network的结果,每一个点代表,训练那个network训练完之后,把它的Hessian拿出来进行计算,所以这边的每一个点,都代表一个network,就我们训练某一个network,然后把它训练训练,训练到gradient很小,卡在critical point,把那组参数出来分析,看看它比较像是saddle point,还是比较像是local minima

• 纵轴代表training的时候的loss,就是我们今天卡住了,那个loss没办法再下降了,那个loss是多少,那很多时候,你的loss在还很高的时候,训练就不动了 就卡在critical point,那很多时候loss可以降得很低,才卡在critical point,这是纵轴的部分
• 横轴的部分是minimum ratio,minimum ratio是eigen value的数目分之正的eigen value的数目,又如果所有的eigen value都是正的,代表我们今天的critical point,是local minima,如果有正有负代表saddle point,那在实作上你会发现说,你几乎找不到完全所有eigen value都是正的critical point,你看这边这个例子里面,这个minimum ratio代表eigen value的数目分之正的eigen value的数目,最大也不过0.5到0.6间而已,代表说只有一半的eigen value是正的,还有一半的eigen value是负的,

所以今天虽然在这个图上,越往右代表我们的critical point越像local minima,但是它们都没有真的,变成local minima,就算是在最极端的状况,我们仍然有一半的case,我们的eigen value是负的,这一半的case eigen value是正的,代表说在所有的维度里面有一半的路,这一半的路 如果要让loss上升,还有一半的路可以让loss下降。

所以从经验上看起来,其实local minima并没有那么常见,多数的时候,你觉得你train到一个地方,你gradient真的很小,然后所以你的参数不再update了,往往是因为你卡在了一个saddle point。

时间序列数据的预处理

• 时间序列数据的预处理
• 如何在实际场景中使用异常检测？阿里云Prometheus智能检测算子来了

在本文中，我们将主要讨论以下几点：

• 时间序列数据的定义及其重要性。
• 时间序列数据的预处理步骤。
• 构建时间序列数据，查找缺失值，对特征进行去噪，并查找数据集中存在的异常值。

时间序列的定义

时间序列是在特定时间间隔内记录的一系列均匀分布的观测值。时间序列的一个例子是黄金价格。在这种情况下，我们的观察是在固定时间间隔后一段时间内收集的黄金价格。时间单位可以是分钟、小时、天、年等。但是任何两个连续样本之间的时间差是相同的。